An Elastic Visco-Plastic Model for Soft Soil with Reference to Radial Consolidation

Abstract

The time-dependent stress–strain behaviour of soft soil due to its viscous nature affects its long-term settlement and pore water dissipation. A novel mathematical model developed using the Peaceman–Rachford ADI scheme (P–R FD Scheme) can describe the visco-plastic behaviour of soft clay with a non-Darcian flow function; this model is a combination of the basic radial consolidation equation developed by Barron and Bjerrum’s time-equivalent (Bjerrum in Geotechnique 17:81–118, 1967) concept that incorporates Yin and Graham’s (Can Geotech J 26:199–209, 1989b) visco-plastic parameters. The settlement and excess pore water pressure obtained from this model are then compared with preexisting models such as a Class C prediction for the Ballina trial embankment at National Field Testing Facility (NFTF). This elastic visco-plastic model provides better results in terms of settlement and pore water pressure with the field data, although the excess pore water pressure that did not dissipate after one year is mainly due to the piezometers becoming biologically and chemically clogged in terrain with acid sulphate soil (ASS).

1 Introduction

The use of vertical drains in soft soil saves a huge amount of time and money because they accelerate the dissipation of pore water and reduce the time needed to reach post consolidation settlement (Bergado et al. 1996; Indraratna et al. 2012; Chu et al. 2000). The dissipation of excess pore water pressure (EPWP) and the rate of settlement are directly influenced by the visco-plastic behaviour of soft clay (Qu et al. 2010; Degago et al. 2011), despite not having an elastic visco-plastic model for radial consolidation that can describe the real behaviour of clay. This paper considers a novel analytical model that will describe the visco-plastic behaviour of soft clay with reference to radial consolidation. This model incorporates the elastic visco-plastic behaviour of soft soil into a consolidation equation derived for the r- and z-directions of a vertical drain and also considers the non-Darcian flow of fluid parameters during radial consolidation. An alternating direction implicit (ADI) finite-difference (FD) method called the Peaceman–Rachford (P–R) method is used to solve the complex partial differential equation and to calculate the settlement and dissipation rate of excess pore water pressure.

2 Elastic Visco-Plastic Model that Considers Non-Darcian Fluid Flow

2.1 Assumptions

The governing equation for radial consolidation with elastic visco-plastic behaviour is based on the non-Darcian flow of fluid and the visco-plastic constitutive relationship by Yin and Graham (1989a), and it captures the Bjerrum time-equivalent constant. The finite-difference (FD) technique is then used to solve the complex nonlinear partial differential equation from which the following assumptions are made:

• (1) The soil is fully saturated and homogeneous.

• (2) The applied load is uniformly distributed and all the compressive strain within the soil element occurs in the radial and vertical directions.

• (3) The drain’s zone of influence is assumed to be circular and axisymmetric.

• (4) The permeability of the drain is infinite compared to the soil.

• (5) The flow of pore water through the soil follows the non-Darcian flow law.

2.2 Derivation

A differential soil element around a vertical drain in a cylindrical coordinate system (as shown in Fig. 1) is considered where the movement of pore water is only allowed in radial and vertical directions (r- and z-directions), and there is no flow in the Ω-direction. In order to satisfy the flow continuity equation, the rate of volume change must be equal to the net flow rate, where ∂V/∂t is given by,

Fig. 1

Coordinates in the r- and z-directions

$$ \frac{\partial V}{\partial t} = \Delta q = \frac{{\partial q_{r} }}{\partial r}{\text{d}}r + \frac{{\partial q_{z} }}{\partial z}{\text{d}}z $$

(1)

$$ q_{r} = v_{r} \left( {r{\text{d}}{\Omega} {\text{d}}z} \right) $$

(2)

$$ q_{z} = v_{z} \left( {r{\text{d}}{\Omega} {\text{d}}r} \right) $$

(3)

where q_r and q_z are the net flow rate in the r- and z-directions, and v_r and v_z are the flow velocities in the r- and z-directions.

The incremental volume change of the soil element $\partial V$ is given by,

$$ \partial V = - \left( {\varepsilon_{r} + \varepsilon_{{\Omega} } + \varepsilon_{z} } \right)\left( {r{\text{d}}{\Omega} {\text{d}}r{\text{d}}z} \right) $$

(4)

where $\varepsilon_{r} ,\varepsilon_{{\Omega} } ,{\text{and}}\,\varepsilon_{z}$ are the strains of the element in the r-, Ω- and z-direction, respectively. By substituting (2), (3), and (4) into Eq. (1),

$$ \frac{{\partial \varepsilon_{v} }}{\partial t} + \frac{{\partial v_{r} }}{\partial r} + \frac{{v_{r} }}{r} + \frac{{\partial v_{z} }}{\partial z} = 0 $$

(5)

The non-Darcian flow relationship proposed by Hansbo (1960) consists of exponential and linear parts, but for simplicity, the power law for the curve is used in this analysis, and it is given by:

$$ v = \alpha_{c} i^{\beta } $$

(6)

where

$v$ :

the flow velocity,

i :

the hydraulic gradient and,

$\alpha_{c}$ and β:

flow constants depending on the type of soil.

The r- and z-components of velocity are given below:

$$ v_{r} = \alpha_{c} \left| {i_{r} } \right|^{\beta } = \alpha_{c} \left| {\frac{1}{{\gamma_{w} }}\frac{\partial u}{\partial r}} \right|^{\beta } $$

(7)

$$ v_{z} = \alpha_{c} \left| {i_{z} } \right|^{\beta } = \alpha_{c} \left| {\frac{1}{{\gamma_{w} }}\frac{\partial u}{\partial z}} \right|^{\beta } $$

(8)

Substituting (7) and (8) into (5),

$$ \frac{{\partial \varepsilon_{v} }}{\partial t} + \frac{{\alpha_{c} \beta }}{{\gamma_{w} {^{\beta }} }}\left[ {\left| {\frac{\partial u}{\partial r}} \right|^{\beta - 1} \left\{ {\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial u}{\partial r}} \right\} + \left| {\frac{\partial u}{\partial z}} \right|^{\beta - 1} \frac{{\partial^{2} u}}{{\partial z^{2} }}} \right] = 0 $$

(9)

Equation (9) is the governing equation for radial consolidation.

According to the Yin–Graham EVP model (Yin and Graham 1989b), strain at any given effective stress is:

$$ \varepsilon_{z} = \varepsilon_{z0}^{\text{ep}} + \frac{\lambda }{V}\ln \frac{{\sigma_{x}^{\prime} }}{{\sigma_{z0}^{\prime} }} + \frac{\psi }{V}\ln \frac{{t_{0} + t_{\text{e}} }}{{t_{0} }} $$

(10)

where $\varepsilon_{z0}^{\text{ep}}$ is the strain at the reference point, (ψ/V) is determined from the slope of creep strain plotted against $\ln \left( {t_{\text{e}} } \right)$, and $t_{\text{e}}$ is the equivalent time.

From Eq. (10), the equivalent time can be calculated by

$$ t_{\text{e}} = - t_{0} + t_{0 } { \exp }\left[ {\left( {\varepsilon_{z} - \varepsilon_{z0}^{\text{ep}} } \right)\frac{V}{\psi }} \right]\left( {\frac{{\sigma_{x}^{\prime} }}{{\sigma_{z0}^{\prime} }}} \right)^{{ - \frac{\lambda }{\psi }}} $$

(11)

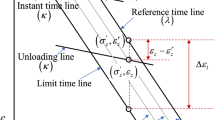
According to the creep model given by Bjerrum (1967) (see Fig. 2):

Fig. 2

Bjerrum time equivalent concept (after Bjerrum 1967)

The incremental strain rate $\frac{{\partial \varepsilon_{z} }}{\partial t}$ based on this figure can be written as:

$$ \frac{{\partial \varepsilon_{z} }}{\partial t} = \frac{\kappa }{{V\sigma^{\prime}_{z} }}\frac{{\partial \sigma^{\prime}_{z} }}{\partial t} + \frac{\psi }{\nu }\frac{1}{{t_{0} + t_{\text{e}} }} $$

(12)

By substituting Eq. (11) into Eq. (12), the elastic visco-plastic model can be obtained as:

$$ \frac{{\partial \varepsilon_{z} }}{\partial t} = \frac{\kappa }{{V\sigma^{\prime}_{z} }}\frac{{\partial \sigma^{\prime}_{z} }}{\partial t} + \frac{\psi }{{t_{0} V}}{ \exp }\left[ { - \left( {\varepsilon_{z} - \varepsilon_{z0}^{\text{ep}} } \right)\frac{V}{\psi }} \right]\left( {\frac{{\sigma_{x}^{\prime} }}{{\sigma_{z0}^{\prime} }}} \right)^{{\frac{\lambda }{\psi }}} $$

(13)

Equation (13) can be rewritten in terms of excess pore pressure by:

$$ \frac{{\partial \varepsilon_{z} }}{\partial t} = \frac{\kappa }{{V(\sigma_{z} - u)}}\frac{{\partial (\sigma_{z} - u)}}{\partial t} + \frac{\psi }{{t_{0} V}}{ \exp }\left[ { - \left( {\varepsilon_{z} - \varepsilon_{z0}^{\text{ep}} } \right)\frac{V}{\psi }} \right]\left( {\frac{{(\sigma_{x} - u)}}{{\sigma_{z0}^{\prime} }}} \right)^{{\frac{\lambda }{\psi }}} $$

(14)

where $\sigma_{z}$ is the total vertical stress.

If the total vertical stress is constant and $\varepsilon_{z0}^{\text{ep}}$ is assumed to be zero, then Eq. (14) becomes:

$$ \frac{{\partial \varepsilon_{z} }}{\partial t} = - m_{v} \frac{\partial u}{\partial t} + g\left( {u,\varepsilon_{z} } \right) $$

(15)

where $g\left( {u,\varepsilon_{z} } \right)$ is a visco-plastic constant term and given by,

$$ g\left( {u,\varepsilon_{z} } \right) = \frac{\psi }{{t_{0} V}} { \exp }\left[ { - \left( {\varepsilon_{z} } \right)\frac{V}{\psi }} \right]\left( {\frac{{(\sigma_{x} - u)}}{{\sigma_{z0}^{\prime} }}} \right)^{{\frac{\lambda }{\psi }}} $$

Combining (9) with (15)

$$ m_{v} \frac{\partial u}{\partial t} - g\left( {u,\varepsilon_{z} } \right) = \frac{{\alpha_{c} \beta }}{{\gamma_{w} {^{\beta }} }}\left[ {\left| {\frac{\partial u}{\partial r}} \right|^{\beta - 1} \left\{ {\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial u}{\partial r}} \right\} + ||\frac{\partial u}{\partial z}|^{\beta - 1} \frac{{\partial^{2} u}}{{\partial z^{2} }}} \right] $$

(16)

2.3 FD Solution of Axisymmetric Equation

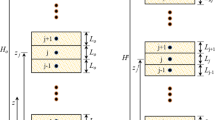
The Peaceman–Rachford alternating direction implicit (ADI) (Murray and Lynn 1965) is a two-step finite-difference method used to solve Eq. (16). In step one, the implicit differentiation is applied in the r-direction and the explicit differentiation in the z-direction gives the predictor; in step two, the implicit differentiation is applied in the z-direction and the explicit differentiation in the r-direction gives the corrector. An intermediate time step t + Δt/2 has been defined for the predictor and corrector, and it lies between t and t + Δt (Fig. 3a).

Fig. 3

a Time steps for P–R ADI scheme and b FD nodes at a given time

The finite-difference grid for this solution is shown in Fig. 3b, where i is the variable along the x-direction which represents the r-coordinates that vary from i − 1, i, and i + 1. Similarly, j is the variable along the y-direction which represents the z-coordinates that vary from j − 1, j, and j + 1. The pore water pressure is calculated at each node of the grid using the P–R ADI scheme.

To simplify Eq. (16), $( {\frac{\partial u}{\partial r}} )^{\beta - 1 }$ and $( {\frac{\partial u}{\partial z}} )^{\beta - 1 }$ are defined at the last time step and continue the iteration process along with the Peaceman–Rachford ADI scheme.

$$ \omega^{t}_{i,j} = \left( {\frac{{u_{i + 1,j}^{t} - u_{i,j}^{t} }}{2\Delta r}} \right)^{\beta - 1} $$

(17)

$$ \varphi^{t}_{i,j} = \left( {\frac{{u_{i,j + 1}^{t} - u_{i,j}^{t} }}{2\Delta z}} \right)^{\beta - 1} $$

(18)

Equation (16) is derived to incorporate the elastic visco-plastic behaviour for soft soil that consists of a linear and nonlinear part of $\left( {\frac{\partial u}{\partial r}} \right)$ and $\left( {\frac{\partial u}{\partial z}} \right)$. This combination of a linear and nonlinear part in a partial differential equation means it cannot be solved in one step so an iterative method for the nonlinear part is applied to the nonlinear flow portion to solve the equation correctly.

The form of equation that should undergo FD-ADI scheme is

$$ \frac{\partial u}{\partial t} = \frac{{\alpha_{c} \beta }}{{\gamma_{w} {^{\beta }} m_{v} }} \left[ {\left| {\frac{\partial u}{\partial r}} \right|^{\beta - 1} \left\{ {\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial u}{\partial r}} \right\} + ||\frac{\partial u}{\partial z}|^{\beta - 1} \frac{{\partial^{2} u}}{{\partial z^{2} }}} \right] + \frac{1}{{m_{v} }}g\left( {u,\varepsilon_{z} } \right) $$

(19)

Applying the FD method to Eq. 19 gives us the predictor and corrector in matrix form:

For each j, the predictor matrix is given by

$$ u_{i,j}^{{t + \frac{\Delta t}{2}}} = C^{\text{I}} + C^{\text{II}} u_{i + 1,j}^{{t + \frac{\Delta t}{2}}} + C^{\text{III}} u_{i - 1,j}^{{t + \frac{\Delta t}{2}}} $$

Similarly, for each i, the corrector matrix is given by

$$ u_{i,j}^{t + \Delta t} = C^{\text{I}} + C^{\text{II}} u_{i,j + 1}^{t + \Delta t} + C^{\text{III}} u_{i,j - 1}^{t + \Delta t} $$

By using the pore water pressure at a different time at each node, the vertical strain at each node can be calculated using the following equation:

$$ \left( {\varepsilon_{z} } \right)_{i,j,t + \Delta t} = \left( {\varepsilon_{z} } \right)_{i,j } - m_{vi,j,t} \left( {u_{i,j,t + \Delta t} - u_{i,j,t} } \right) + \Delta tg\left( {u,\varepsilon_{z} } \right)_{i,j} $$

(20)

This entire computation is carried out using a finite-difference technique by adopting forward, backward, and central difference techniques. For this purpose, a user-friendly program is written into MATLAB in a tri-diagonal matrix form and executed with settlement and pore water pressure as an output.

3 Validation and Discussions

This elastic visco-plastic model has been validated using a Class C (Lambe 1973) prediction exercise from the Ballina Embankment. A Class A prediction of the Ballina embankment was carried out before construction, and a Class C prediction was carried out after field data became available. The Class A Prediction based on industry standard data and large-scale consolidometer (350 mm large specimen: see Fig. 4) matches the initial rate of settlement and ultimate settlement quite accurately, although a large error arose due to the absence of a creep model in our Class A prediction method. The inclusion of visco-plastic behaviour (i.e. creep) made the prediction more accurate and is thus defined as a Class C prediction. The same case history is utilised in this paper to validate the novel mathematical model.

Fig. 4

Large-scale consolidometer (modified after Indraratna and Redana 2000)

A 3-m-high embankment with a 80 m long × 15 m wide crest has been constructed with a 1.5H: 1V side slope. There is a 95 m long × 25 m wide × 1 m high working platform on the existing ground surface to provide top drainage and facilitate drain installation. This embankment has three sections: Two sections are 30 m long and contain conventional PVD wick drains and biodegradable jute drains, while the third section is 20 m long and contains conventional PVD drains with a geotextile layer instead of a sand drainage layer. A suite of instruments such as inclinometers, magnetic extensometers, settlement plates, vibrating wire piezometers, and hydraulic profile gauges has been installed to monitor embankment behaviour (see Fig. 5). This embankment was constructed in stages over a 60-day period. The compacted bulk density of the sand drainage layer (0.6–1 m thick) is 15.9 kN/m³ while the compacted density of the above fill is 20.6 kN/m³; this results in a total surcharge load of 59.8 kN/m³. The vertical drains are 14–15 m deep; they were installed using a rectangular mandrel with a 120 mm × 60 mm cross section and an 80 t drain stitcher. There are 190 mm × 90 mm rectangular plates attached to the tip of the mandrel to act as drain anchors while the drains were installed in a square pattern at 1.2 m spacing.

Fig. 5

Layout of embankment

The sub-soil profile consists of an almost 0.2 m thick layer of organic material (decomposing sugar cane plants), below which there is a 1 m thick layer of sandy clayey silt, and a very plastic 8.8 m thick layer of silty clay. Beneath these layers, there is a 4-m-thick transition zone consisting of large amounts of sand, followed by a 5 m thick layer of fine sand (see Fig. 6). This deposit can be classified as highly compressible marine clay with very low permeability and high plasticity (CH). At most depths of the upper Holocene layer, the natural water content is very close to their liquid limits.

Fig. 6

Basic soil properties of Ballina clay (modified from Pineda et al. 2016)

All the soil parameters and drain parameters needed to solve the elastic visco-plastic model are listed in Table 1. When they are input into a MATLAB-coded interface of EVP-FDM model (Indraratna et al. 2018), the behaviour of embankment in terms of settlement and excess pore water pressure is obtained as an output. The staged construction of the embankment, the surface settlement, and the excess pore water pressure at 6 m depth are plotted in Fig. 7.

Table 1 Soil and drain properties used for the predictions

Fig. 7

Settlement and EPWP prediction with field data (modified from Indraratna et al. 2018)

As Fig. 7 shows, the Class C prediction using an EVP-FDM model yields better predictions in terms of surface settlement, whereas the excess pore pressures are still at much higher levels than the predicted values, especially after 1–1.5 years, due to the piezometer tips becoming biologically and chemically clogged in highly prone ASS terrain (Indraratna et al. 2017). In acid sulphate floodplains, piezometers are influenced by tidal intrusion and flooding (they must be corrected when determining the excess pore water pressure), filter corrosion or chemical alteration in acidic groundwater, armouring by minute rust particles (i.e. precipitated iron oxide), the formation of biomass due to acidophilic bacteria, and associated gas cavitation, as well as potential physical clogging by very fine (dispersive) particles over time. Embankments constructed in acid sulphate soil floodplains with a large organic content may experience climatic and biological (bacterial) factors that cause vibrating wire piezometers to become inaccurate over time because their filters cannot be flushed after installation, unlike standpipes that can be maintained.

4 Conclusion

To summarise, the elastic visco-plastic (EVP) model could capture the non-Darcian fluid flow in radial consolidation based on Yin and Graham’s EVP parameters and Bjerrum’s time equivalent concept, while the two-step finite-difference method known as Peaceman–Rachford (P–R) was applied to the governing equations of radial consolidation to make the solution more accurate by performing the calculations consecutively using predictor and corrector. This approach means that embankment behaviour in terms of surface settlement and excess pore water pressure has been predicted very accurately using the proposed EVP-FDM model. The minor discrepancy while predicting excess pore water pressure is inevitable which is due to chemical and biological clogging of piezometer tips after almost a year especially in acid sulphate soil (ASS) terrain where oxidisable pyrite layers are present within relatively shallow depths of the upper Holocene clay. Further research on biological chemical clogging of piezometer tips in ASS terrain through industry linkages is now underway to identify the types of bacteria causing potential clogging of ceramic filters over time and to identify the possible benefit of using other materials as a filter tip to develop technically sound and cost-effective corrective measures for piezometers at University of Wollongong.