Electricity for Fluidics and Bio-Devices

Abstract

This chapter is focused on biomaterial interaction with electromagnetic fields. It gives a wide and deep introduction of biological medium and their electromagnetic properties, which can be used to sense and analyze tissue or cells within lab-on-chip. It consists of three complementary parts. A recall of electrokinetics laws is done and is applied to biological medium (electrolyte with fluid motion) in the first section. The scaling factor towards nano-scale is highlighted considering the ionic concentration distribution. The second section deals with dielectrophoresis forces (DEP), which results from the cell polarization under non-uniform electric field. The dielectric modeling of cells and their DEP response are depicted. Taking benefits of cell dielectric behavior, the applications such as cell sorting, trapping and characterization with electrorotation are presented. The last section introduces the biomaterial behavior at radiofrequency range (from MHz up to several tens of GHz). Applications using thee relaxation times occurring at such high frequency are described to sense or characterize biological medium. Electric Impedance Spectroscopy and Radio-Frequency devices are thus introduced.

6.1 Introduction

From an electrical engineering point of view, biological materials can be seen as heterogeneous conductive materials. In fact, the human body is mainly composed of liquid medium (water) where charged particles (such as sodium or chloride atoms, proteins) can flow. Under electric field, this ionic composition induces a current flow, which can be monitored. Concerning the biological cell, the lipid bilayer of cellular membrane behaves as an electrical insulator and thus modifies the flow path of the ions in relation with the cellular state, localization and numbers. Furthermore, the water is a dielectric material and its polarization also interacts with the electric field. Thus the human body, organ or cell can be seen as complex electrolyte within which the electric field can be used to sense or act on polarizable particles.

In this chapter, the physics of electrokinetic phenomena will be first presented and applied at nano-scale. Applications will be then depicted concerning handling and sensing cells using dielectrophoresis within lab-on-chip. Results will be then extended towards bioimpedance analysis for biomaterial dielectric properties extraction using large frequency range of the electric field, from kHz up to several GHz.

6.2 Micro- and Nano-Scale Electrokinetics (Hyomin Lee and Sung Jae Kim)

6.2.1 Introduction to Nonlinear Nanoscale Electrokinetics

There has been considerable interest over the past decade in the science and engineering of fluid transport at micrometer and nanometer scales [1,2,3,4]. Advances in micro- and nano-electromechanical system (MEMS and NEMS) technology over the past few decades have allowed miniaturized devices to be developed for various micro- and nano-fluidic applications. These miniaturized platforms offer significant advantages compared to conventional bulk analytical instruments: they support precise control of liquids flowing usually under laminar regime, minimize consumption of reagents and samples, favor short reaction times, enable highly parallel and multiplexed analysis, require less power to operate, and potentially have low cost of production [1]. For these advantages, electrokinetic mechanisms have been usually used as the preferred method of transporting fluids in the miniaturized systems because of the ease and low cost of electrode fabrication, excluding moving mechanical parts, and the significant effect of the electric double layer which is the thin polarized layer in the liquid adjacent to the charged surface. Due to these reasons, many seminal works to describe the electrokinetic phenomena in microscale system have been established [1, 5,6,7].

Nevertheless, electrokinetic phenomena in nanoscale system are not still obvious. In the nanoscale system, the electric double layer would be overlapped so that its equilibrium structure could not be maintained under external driving field [8, 9] called as non-equilibrium state. Conventional theories for microscale system are only applicable to the electric double layer under equilibrium limit. In addition, several factors, usually neglected in microscale system, could play an important role for nanoscale transport phenomena when the system dimension decreased. For example, hydrodynamic slip on solid surface could be occurred [10, 11], while “no slip” condition is usually applied in microscale system. In viewpoints of conventional theories, fluid molecules were attached to solid surface so that they could not move. This is known as ‘no-slip condition’ on liquid-solid interfaces. However, in actual system, fluid molecules on the interface are not attached to the interface strongly so that they could be movable. This is called as slippage of fluid molecule. Due to this slippage, ionic current could be higher than the value predicted by conventional theories for microscale system. Another example among unique properties of nanofluidic system is ‘surface-charge-governed conductance’. Ionic transport in nanofluidic systems have the unique property of surface-charge-governed regime as demonstrated by Stein et al. [12]. In a dilute limit, ionic conductance is independent from the bulk properties of the system such as the electrolyte concentration or the geometrical factor, so that the conductance curve saturates below a specific concentration value, which is determined by surface charge density and called ‘surface-charge-governed conductance’. Because the plateau of the conductance curve is only revealed in a nanochannel system, this property has been utilized to demonstrate the validity of the device in the view point of nanofluidic application. Beyond the specific concentration value, the conductance is proportional to the bulk concentration, called ‘geometry-governed regime’. These two distinct regimes can be plotted (ionic conductance as a function of bulk concentrations) simultaneously. Since these unique properties were usually neglected in microscale electrokinetic analysis, direct application of the conventional theory could cause non-negligible errors in nanoscale electrokinetic analysis. Thus, aims of recent researches in nanoscale electrokinetics were (1) finding new constraints to describe the unique property of nanoscale, which has never been observed in microfluidic system, (2) establishing the modified model using the new constraints, and (3) predicting the phenomena, which are difficult to observe by experimental manner. To exemplify these concerns, the contents of this book focused on nanoscale electrokinetic transport phenomena inside the nanoscale system (ionic field effect transistor, a.k.a IFET) and nearby the system (ion concentration polarization, a.k.a. ICP) which are the most relevant phenomenon occurs in the biological system, especially inside human body.

At first, governing equations and appropriate boundary conditions for the nanoscale system were revisited from general conservation principle as written in Sect. 6.2.2. In this chapter, fundamental equations such as the Poisson equation, the Nernst-Planck equations, Stokes equations, and the continuity equation could be found, which are used as governing equations in other chapters.

In Sect. 6.2.4, the model to describe ion concentration polarization (ICP) phenomenon was discussed. The micro-nano hybrid system, which is composed of microchannel reservoir—perm-selective nanoporous membrane—microchannel reservoir and also resembled the cellular structure, has unique phenomenon of as ICP. Through the perm-selective nanoporous media, only counter-ion can be transported across the media while co-ion cannot. Because of the selectivity of transported species, ion concentration is decrease on one side (this is called ‘depletion’), while on the other side ion concentration is increase (this is called ‘enrichment’). This is called as ‘ion concentration polarization’. For various applications such as desalination [13], preconcentration [14], and battery system [15, 16], the concentration distribution inside the depletion and enrichment zone should be the key feature to apply these applications.

Furthermore, we suggested the model to describe the gate modulation in the partially gated ionic field effect transistor. The ionic field effect transistor (IFET) as a nanofluidic device could change the polarity of the nanochannel or nanopore so that the permselectivity, unique property of nanoscale system, which permits only counter-ion pass through the nanoscale system, could be controlled. Using this functionality, switching of macromolecules such as DNA, RNA, and proteins [17] or ionic species such as cation and anion [18, 19] could be possible. In the field of IFET research, the description for the polarity modulation by gate electrode in IFET has been an important issue.

6.2.2 Conservation Principles of Electrokinetic System

Three fundamental conservation principles are needed to describe the transport phenomena in the electrokinetic system. Because the typical electrokinetic system involves a fluid motion u with ionic species which have electric charge, independent variables such as electric potential ψ, concentration of each ionic species cj and hydrodynamic pressure p should be required for the characterization of the system. Each independent variable is related to the conservation principle; (1) the electric potential is related to conservation of electric charge, (2) concentration of ionic species is associated with the conservation of mass, and (3) hydrodynamic pressure and flow field is connected with the conservation of mass and momentum. Therefore, in this chapter, governing equations and boundary conditions for electrokinetic system will be introduced from a viewpoint of conservation principles under the continuum framework which is held down to a length scale greater than 1 nm [10]. Although some other models have been proposed to try to integrate the discrete effect of ion transport or fluid flow in the continuum frameworks with an extra term [20] or by adapting the results of molecular dynamics [21], continuum hypothesis still remain intact in most electrokinetic system.

6.2.2.1 Conservation of Electric Charge

Most electrokinetic systems immersed in an electrolyte solution attain electric charge distribution due to charged surface and ionized species. The electrostatic forces arising from the interactions between them plays essential role in the transport phenomena in the electrokinetic system. In order to describe the electrostatic system, the governing equation and appropriate boundary conditions will be introduced briefly.

The Maxwell’s equations are not limited to the electrostatic system. The equations relate the electric field E and the magnetic field H to material properties, the charge density, and conservation principles. The full set of Maxwell’s equations in general form is

$$ \nabla \cdot {\mathbf{D}} = \rho_{\text{f}} $$

(6.1)

$$ \nabla \cdot {\mathbf{B}} = 0 $$

(6.2)

$$ \nabla \times {\mathbf{E}} = - \frac{{\partial {\mathbf{B}}}}{\partial t} $$

(6.3)

and

$$ \nabla \times {\mathbf{H}} = \frac{{\partial {\mathbf{D}}}}{\partial t} + {\mathbf{J}}_{\text{f}} . $$

(6.4)

Here, D is the electric displacement vector, ρ_f is the free charge density, B is the magnetic induction field, E is the electric field, H is the magnetic field, and J_f is the conduction current density associated with the movement of free charge. For a linear and homogeneous dielectric medium, the following constitutive relationship can be written

$$ {\mathbf{D}} = \varepsilon {\mathbf{E}} $$

(6.5)

and

$$ {\mathbf{B}} = \mu {\mathbf{H}} $$

(6.6)

where ε is the dielectric permittivity and μ is the magnetic permeability of the medium. Utilizing Eqs. (6.5) and (6.6), the Maxwell equations can be written for a linear homogeneous dielectric medium as

$$ \nabla \cdot {\mathbf{E}} = \frac{{\rho_{\text{f}} }}{\varepsilon } $$

(6.7)

$$ \nabla \cdot {\mathbf{H}} = 0 $$

(6.8)

$$ \nabla \times {\mathbf{E}} = - \mu \frac{{\partial {\mathbf{H}}}}{\partial t} $$

(6.9)

and

$$ \nabla \times {\mathbf{H}} = \varepsilon \frac{{\partial {\mathbf{E}}}}{\partial t} + {\mathbf{J}}_{\text{f}} . $$

(6.10)

It is clear from the above equations that when the electric field varies with time, one needs to consider the magnetic field as well. In this case, the equations governing the electric and magnetic fields are coupled. However, in most of electrokinetic system, the effect of the magnetic field can be negligible or the system is under static case i.e. the absence of time variation so that electric field can be decoupled from the magnetic field. Therefore, the Maxwell’s equations for describing the typical electrokinetic system can be reduced in the following form:

$$ \nabla \cdot {\mathbf{E}} = \frac{{\rho_{\text{f}} }}{\varepsilon } $$

(6.11)

$$ \nabla \times {\mathbf{E}} = {\mathbf{0}}. $$

(6.12)

Because the electric field is curl-free, electric field can be represented by gradient of scalar quantity ψ known as electric potential. Hence, the governing equation for conservation of electric charge is

$$ \nabla \cdot (\varepsilon \nabla \psi ) = - \rho_{\text{e}} $$

(6.13)

with the fundamental relationship between the irrotational field and the scalar potential as

$$ {\mathbf{E}} = - \nabla \psi . $$

(6.14)

Next, we will briefly introduce the appropriate boundary conditions for electrostatic problems. For electrostatic systems, the Gauss law can be applied to the boundary between two domains to determine the boundary conditions for the normal and tangential components of the electric field. The Gauss law relates the electric field through a closed surface to the enclosed charge and can be denoted as

$$ \oint_{S} {\mathbf{E}} \cdot {\mathbf{n}}{\text{d}}S = \frac{Q}{\varepsilon } $$

(6.15)

where S is bounded surface of arbitrary volume V, n is the outward normal to the surface S, and Q is the total charge inside the volume V. Given an interface with a charge per unit area given by σs, separating two domains labeled 1 and 2 with two permittivity of ε₁ and ε₂, respectively, the boundary condition for the normal component of the electric field is given by

$$ \varepsilon_{1} {\mathbf{E}}_{1} \cdot {\mathbf{n}}_{1} - \varepsilon_{2} {\mathbf{E}}_{2} \cdot {\mathbf{n}}_{2} = \sigma_{\text{s}} . $$

(6.16)

In the above expression, the direction of n₁ points from domain 2 to domain 1. A line integral over a loop at the boundary gives the following boundary condition for any tangent component of the electric field;

$$ {\mathbf{E}}_{1} \cdot {\mathbf{t}} = {\mathbf{E}}_{2} \cdot {\mathbf{t}}. $$

(6.17)

Equation (6.17) holds for any unit vector tangent to the surface. Boundary conditions (6.16) and (6.17) can be represented in terms of electric potential so that

$$ - \varepsilon_{1} \frac{{\partial \psi_{1} }}{{\partial n_{1} }} + \varepsilon_{2} \frac{{\partial \psi_{2} }}{{\partial n_{2} }} = \sigma_{s} $$

(6.18)

and

$$ \psi_{1} = \psi_{2} $$

(6.19)

which are hold at the interface between two domain.

There are widely used boundary conditions for microscale or nanoscale electrokinetic system. For a reservoir or electrode surface where the electric potential is applied, the electric potential is specified.

$$ \left. \psi \right|_{\text{ reservoir }} = V_{0} $$

(6.20)

where V₀ is the specified value of the applied potential. Because reservoirs of microdevice are typically considered as an enormous source of ions compared with the microchannels themselves, any voltage drop can be neglected between the electrode and the inlet or outlet to the microchannel. For an insulating wall that has surface charge density σ_s, Eq. (6.18) is simplified because the electric field in the insulating wall (E₂) normal to the surface is approximately zero. Thus the normal boundary condition is a relation between the surface charge density and the potential gradient normal to the surface,

$$ \left. {\frac{\partial \psi }{\partial n}} \right|_{\text{wall}} = - \frac{{\sigma_{\text{s}} }}{\varepsilon }. $$

(6.21)

Typically, the material of the channel is SiO₂, Al₂O₃, or PDMS of which relative permittivity is lower than 10 so that channel wall can be treated as insulating material and Eq. (6.21) is a reasonable approximation. When the relative permittivity of the channel wall cannot be neglected or the electrostatics inside the solid is important, Eqs. (6.18) and (6.19) should be used together. These are summarized in Table in Sect. 6.2.2.4.

6.2.2.2 Conservation of Mass

This section describes the phenomena that lead to flux of charged ionic species in the dilute limit. These fluxes lead to the Nernst-Planck equations. Although certain conditions, i.e. high concentration and high applied voltage, would violate the dilute approximation, we will discuss only the conservation of mass in the dilute limit. The effect of the non-dilute condition will be reconsidered in Sect. 6.2.4 because the effect cannot be negligible in nanometer scale system.

Firstly, we will consider the diffusion flux of the ionic species when concentration gradient is existed. In the dilute limit, Fick’s law defines a flux density of species proportional to the gradient of the species concentration and the diffusivity of the species in the solvent as

$$ {\mathbf{j}}_{{{\text{diff, }}i}} = - D_{i} \nabla c_{i} $$

(6.22)

where j_diff,i is the diffusive species flux density i.e. the amount of species i moving across a surface per unit area due to diffusion, D_i is the diffusivity of species i in the solvent (usually water), and c_i is the concentration of species i. Fick’s law is a macroscopic way of representing the summed effect of the random motion of species owing to thermal fluctuations. Fick’s law for thermal energy flux caused by a temperature gradient and the Newtonian model for momentum flux induced by a velocity gradient, and the species diffusivity D_i is analogous to the thermal diffusivity α = k/ρ Cp and the momentum diffusivity η/ρ.

Second flux is the convective flux of the ionic species when there is an ambient fluid flow. Its form is

$$ {\mathbf{j}}_{{{\text{conv}},i}} = c_{i} {\mathbf{u}} $$

(6.23)

where j_conv,i is the convective species flux density i.e. the amount of species i moving across a surface per unit area due to an ambient fluid flow u.

Third flux is the migration flux of the ionic species due to an external force such as electric field in usual electrokinetic system. The migration flux can act differently on different species in general. Let us denote the force acting on one ionic species by F_ext, which is applied external force. The ionic species will move under the influence of this external force, and one can write its migration velocity V_i as

$$ {\mathbf{v}}_{i} = \omega_{i} {\mathbf{F}}_{\text{ext}} $$

(6.24)

where ω_i is defined as the mobility of the species (velocity per unit applied force). The migration flux can be defined as

$$ {\mathbf{j}}_{{\text{mig} ,i}} = c_{i} {\mathbf{v}}_{i} = c_{i} \omega_{i} {\mathbf{F}}_{\text{ext}} . $$

(6.25)

At this point, we need to interpret the mobility ω_i, which was introduced in Eq. (6.24). Normally, application of a force to a mass causes it to accelerate so that assigning a constant velocity to the particle as in Eq. (6.24) seems counter-intuitive. However, it should be noted that as soon as a solute particle starts to move under the influence of the external force, it encounters a counteracting drag force due to the other particles (predominantly solvent) surrounding it. Consequently, it is assumed that the solute particle moves at a terminal velocity attained under the combined influence of the external force and the frictional drag force of the surrounding medium. This is a grossly simplified view of the migration velocity and Einstein showed that

$$ \omega_{i} = \frac{{D_{i} }}{{k_{B} T}} $$

(6.26)

where k_B is the Boltzmann constant and T is the absolute temperature of the surrounding. Substituting Eq. (6.26) in Eq. (6.25), one obtains

$$ {\mathbf{j}}_{{{\text{mig}},i}} = \frac{{D_{i} }}{{k_{B} T}}c_{i} {\mathbf{F}}_{\text{ext}} . $$

(6.27)

As earlier mentioned, Fext is usually the external electric field for electrokinetic system so that Fext can be represented by

$$ {\mathbf{F}}_{\text{ext}} = - z_{i} e\nabla \psi $$

(6.28)

where z_i is the valence of the ionic species and e is the elementary charge. Therefore, the migration flux of the ionic species can be expressed in terms of the independent variables of electrokinetic system.

$$ {\mathbf{j}}_{{{\text{mig}},i}} = - \frac{{z_{i} eD_{i} }}{{k_{B} T}}c_{i} \nabla \psi = - \frac{{z_{i} FD_{i} }}{RT}c_{i} \nabla \psi $$

(6.29)

where F is the Faraday constant and the R is the gas constant.

In above representations for ionic flux in terms of each transport mechanism, total ionic flux j_i can be expressed by

$$ {\mathbf{j}}_{i} = {\mathbf{j}}_{{{\text{diff}},i}} + {\mathbf{j}}_{{{\text{mig}},i}} + {\mathbf{j}}_{{{\text{conv}},i}} = - D_{i} \nabla c_{i} - \frac{{z_{i} FD_{i} }}{RT}c_{i} \nabla \psi + c_{i} {\mathbf{u}}. $$

(6.30)

Due to the conservative nature of chemical species with no chemical reaction, total ionic flux should be satisfied with

$$ \nabla \cdot {\mathbf{j}}_{i} = \nabla \cdot \left( { - D_{i} \nabla c_{i} - \frac{{z_{i} FD_{i} }}{RT}c_{i} \nabla \psi + c_{i} {\mathbf{u}}} \right) = 0. $$

(6.31)

When there are chemical reactions, Eq. (6.31) becomes

$$ \nabla \cdot {\mathbf{j}}_{i} = \nabla \cdot \left( { - D_{i} \nabla c_{i} - \frac{{z_{i} FD_{i} }}{RT}c_{i} \nabla \psi + c_{i} {\mathbf{u}}} \right) = R_{i} $$

(6.32)

where R_i is the reaction rate of chemical species i. Equation (6.32) is known as the Nernst-Planck equations which imply the conservation of mass in terms of concentration of species i.

Widely used boundary conditions for Nernst-Planck equations are (1) specified concentration and (2) specified ionic normal flux. Firstly, specified concentration condition is used for reservoir, inlet, or outlet of the system. When the concentration is known at the boundary, condition is

$$ \left. {c_{i} } \right|_{\text{reservoir }} = c_{0} $$

(6.33)

where c₀ is the known concentration at the boundary. Secondly, specified ionic normal flux is chosen in the case of channel wall, chemically reactive surface, or inlet/outlet under a forced transport mechanism. The general form of this type of boundary is

$$ {\mathbf{n}} \cdot {\mathbf{j}}_{i} \left| {_{\text{boundary }} } \right. = {\mathbf{n}} \cdot {\mathbf{j}}_{0} $$

(6.34)

where j₀ is the known expression of ionic flux though the boundary. When boundary is channel wall, j₀ = 0 which means any species cannot penetrate through the boundary. When boundary is chemically reactive surface, j₀ is a function of surface reaction rate. In case of inlet/outlet under a forced transport mechanism, j₀ is fixed to a function of relating transport mechanism. For example, when forced convection is on inlet or outlet, j₀ becomes c₀u|_boundary.

6.2.2.3 Conservation of Momentum

In this section, we discuss the Stokes equation for the conservation of momentum and the continuity equation. In typical electrokinetic system, there are fluid flows induced by ion movement driven by external forces. Thus, fluid motion should be considered and this is governed by the conservation of momentum. The Reynolds number of usual microscale or nanoscale electrokinetic system is low so that viscous forces dominate over inertial forces. As a result, the Navier-Stokes equations can be reduced to the Stokes equations which are linear differential equations so that the Stokes equations are easier to solve than the Navier-Stokes equations.

The flow of the Newtonian fluid system under laminar flow conditions with constant density and viscosity is governed by the momentum conservation equation and is given by the Navier-Stokes equations [22].

$$ \rho \frac{{\partial {\mathbf{u}}}}{\partial t} + \rho {\mathbf{u}} \cdot \nabla {\mathbf{u}} = - \nabla p + \eta \nabla^{2} {\mathbf{u}} + \rho {\mathbf{g}} + {\mathbf{F}}_{\text{b}} . $$

(6.35)

Equation (6.35) represents the force balance on a fluid element in space. Here ρ is the density of the fluid, t is the time, u is the flow velocity field, p is the pressure, η is the viscosity of the fluid, g is the gravitational acceleration, and F_b is the body force acting on the fluid element in addition to the gravity. In electrokinetic transport processes, one needs to consider the electrical body force acting on the fluid. Further discussion on the electrical body force will be presented later in this section.

Each term of Eq. (6.35) represents forces acting on a unit volume of the fluid. The first term on the left hand side represents the rate of change of momentum at a given location within the flow field. For steady conditions, this term drops out. The second term is due to the fluid inertia and is negligible for low Reynolds number flows [23] and this will be shown in later. The first term of the right hand side represents the contribution of pressure, the second term is due to viscous forces, the third term arises from the body force due to gravity, and the last term arises from other body force which is usually electrical body force in the electrokinetic system. Equation (6.35) can be written for any orthogonal coordinate system [22].

Although the conservation of momentum can be described by the Navier-Stokes equations, it is difficult to solve the equations because of nonlinearity of the inertial term. Thus, we derive the Stokes equations by neglecting the unsteady and inertial terms when the viscous force is dominant. Equation (6.35) is rewritten in non-dimensional form in which the length scale is L_c, the velocity scale is U_c, the pressure scale is η U_c/L_c, and the time scale is L_c/U_c.

$$ Re\left( {\frac{{\partial {\tilde{\mathbf{u}}}}}{{\partial \tilde{t}}} + {\tilde{\mathbf{u}}} \cdot \, \widetilde{\nabla }\widetilde{{\mathbf{u}}}} \right) = - \widetilde{\nabla }\tilde{p} + \widetilde{\nabla }^{2} {\tilde{\mathbf{u}}} + {\tilde{\mathbf{g}}} + {\tilde{\mathbf{F}}}_{\text{b}} . $$

(6.36)

Above expression is non-dimensional form of the Navier-Stokes equations. A tilde denotes dimensionless variable. Re is the Reynolds number, defined by R_e = ρU_cL_c/η of which meaning is the ratio of inertial force and viscous force acting on a fluid element. Considering the microscale or nanoscale electrokinetic system, R_e is usually much smaller than 1 so that R_e can be approximated to 0. Therefore, the left hand side of Eq. (6.36) is negligible. Consequently, following equations are called as Stokes equations with body force terms.

$$ {\mathbf{0}} = - \nabla p + \eta \nabla^{2} {\mathbf{u}} + \rho {\mathbf{g}} + {\mathbf{F}}_{\text{b}} . $$

(6.37)

For convenience, the term of gravity force merge into pressure so that modified pressure is usually used rather than original hydrodynamic pressure.

As earlier discussed, the momentum equation given by Eq. (6.37) contains a generic body force term, F_b which can be used to consider any type of force acting on a fluid volume element. In electrokinetic transport processes, this body force arises due to an electric field. The electric body force per unit volume on the fluid, F_E is given by [24]

$$ {\mathbf{F}}_{\text{E}} = \rho_{\text{f}} {\mathbf{E}} - \frac{1}{2}{\mathbf{E}} \cdot {\mathbf{E}}\nabla \varepsilon + \frac{1}{2}\nabla \left[ {\left( {\rho \frac{\partial \varepsilon }{\partial \rho }} \right)_{T} {\mathbf{E}} \cdot {\mathbf{E}}} \right] $$

(6.38)

which is derived from the Korteweig-Helmholtz electric for a linear dielectric medium. For the special case of a constant dielectric permittivity and an incompressible fluid, the electrical body force becomes

$$ {\mathbf{F}}_{\text{E}} = \rho_{\text{f}} {\mathbf{E}}. $$

(6.39)

Recognizing that the electric field E is related to the electric potential ψ, the body force is represented as

$$ {\mathbf{F}}_{\text{E}} = - \rho_{\text{f}} \nabla \psi . $$

(6.40)

Introducing the electric force term for the body force in Eq. (6.37), we obtain the following governing equations for conservation of momentum in the electrokinetic system as

$$ {\mathbf{0}} = - \nabla p + \eta \nabla^{2} {\mathbf{u}} - \rho_{\text{f}} \nabla \psi . $$

(6.41)

Additionally, the mass conservation for a fluid is also required to solve the Stokes equations. The general form of the mass conservation for the fluid is given by [24]

$$ \frac{\partial \rho }{\partial t} + \nabla \cdot (\rho {\mathbf{u}}) = 0. $$

(6.42)

For the incompressible fluid, the density of the fluid is constant so that

$$ \nabla \cdot {\mathbf{u}} = 0 $$

(6.43)

which is called as the continuity equation for the incompressible fluid. Equations (6.41) and (6.43) are the governing equations for usual electrokinetic system.

The Stokes equations and the continuity equation can be solved after setting appropriate boundary conditions corresponding to a given flow situation. The boundary conditions can specify the velocities or pressures at given locations of the flow boundary. Of particular interest with respect to boundary conditions for these equations is the no-slip condition, which is generally applied at the solid boundaries and this condition is

$$ \left. {\mathbf{u}} \right|_{\text{ boundary }} = {\mathbf{U}}_{0} $$

(6.44)

where U₀ is the specified velocity. The no-slip condition implies that the fluid in contact with a solid object moves at the same velocity as the object. If the object is stationary such as the wall of microchannel, then the fluid velocity is zero at the surface. Imposition of the no-slip condition usually sets up a velocity gradient in the fluid near the solid-fluid interfaces. Such a gradient gives rise to a viscous stress. The local hydrodynamic stress tensor at a point on the surface on the solid surface is given by

$$ {\varvec{\upsigma}}^{\text{H}} = - p{\mathbf{I}} + \eta \left( {\nabla {\mathbf{u}} + \nabla {\mathbf{u}}^{\text{T}} } \right) $$

(6.45)

where σ^H is the hydrodynamic stress tensor, I is the unit tensor, the superscript T means the transpose of the tensor, and the final term on the right hand side represents the viscous stresses. This hydrodynamic stress can be integrated over the surface of the solid object to determine the total hydrodynamic force acting on the object.

6.2.2.4 Coupled Conservation Principles

For the electrokinetic system, independent variables are the electric potential (ψ), ion concentration of i-th species (c_i), pressure (p), and flow field (u) obtained by Eqs. (6.13), (6.32), (6.41), and (6.43) which are derived from conservation principles. Each independent variable is a function of other variables. For example, the electric potential is a function of the ion concentration, the ion concentration is a function of the electric potential and flow field, and flow field is a function of pressure, ion concentration, and electric potential. This situation is called that governing equations are coupled. Thus, governing equations should be solved by coupled manner as similar as simultaneous algebraic equations. Accordingly, coupled governing equations and boundary conditions are summarized in Table 6.1.

Table 6.1 Governing equations and appropriate boundary conditions

6.2.3 Microscale Electrokinetics

Electrokinetics has referred the branch of electrodynamics, which treats the laws of the electrical current, but it should contain rigorous consideration of electrolytic current as well. Recent studies have generally defined the electrokinetic phenomenon as the general term associated with the relative motion between two electrically charged phases, i.e. liquid and solid. Staring from pollutant removal using electric field in the soil science area, the fields of application using the electrokinetic phenomenon has been widen various research fields as shown in Fig. 6.1. With aids of splendid advances in micro/nanofabrication and manufacturing technology, the electrokinetics have been applied to precise medicines, drug discovery and separation science in (bio-) medical engineering and complex fluids, colloid science and micro/nanofluidic in physics area. Among such advances, the major phenomena associated with human internal body structure, electroosmosis has been regarded as the major key elements to understand the biological transport phenomena. Other electrokinetic phenomena such as electrophoresis, dielectrophoresis, induced charge electrokinetics, electrowetting, streaming potential, sedimentation potential, etc. were not covered in this book because their engineering applications focused on problems other than phenomena occurred inside biological system.

Fig. 6.1

The applications of electrokinetic phenomenon

6.2.3.1 Equilibrium Electroosmosis

Electroosmosis is the motion of liquid induced by an applied electric potential across a porous material, capillary tube, membrane, microchannel, or any other fluid conduit. It is an essential component in separation science, especially capillary electrophoresis. It can occur in natural unfiltered water, human body fluid, buffer solutions and highly concentrated brine as well. Discovered by F. F. Reuss in 1809, water migrated through porous clay diaphragms toward the cathode under the influence of electric field since mineral particles are generally negatively charged. The physics behind electroosmosis is shown in the schematics (Fig. 6.2). Once solid conduit was filled with electrolyte solution, ions in the solution attack the surface so that the surface become to have electrical charges. The charges attract counter-ions to form a thin electrical double layer which has counter-ion rich region, while the center (or bulk) of the conduit remains electro-neutral status. With an external electric potential gradient, the ions inside the electrical double layer migrated toward their counter electrode and the water in the conduit is drawn by the ions due to viscous drag and therefore, flows through the conduit. This situation was governed by Navier-Stokes equations with electrical body forces as

Fig. 6.2

Schematic diagram of electroosmosis

$$ \rho \left( {\frac{{\partial {\mathbf{u}}}}{\partial t} + {\mathbf{u}} \cdot \nabla {\mathbf{u}}} \right) = - \nabla p + \mu \nabla^{2} {\mathbf{u}} + \rho {\mathbf{g}} + \rho_{e} {\mathbf{E}}. $$

(6.46)

Since the conduit where the drag forces dominant to induce electroosmosis has under microscale dimension, the equations is simplified in a steady Stokes flow with electrical body force, with neglecting gravity force and pressure gradient as

$$ \mu \nabla^{2} {\mathbf{u}} = - \rho_{e} {\mathbf{E}}. $$

(6.47)

Compared to a pressure driven flow, electroosmosis is surface driven flow so that one can assume thin electrical double layer approximation for a slip velocity known as Helmholtz-Smoluchowski slip velocity defined as

$$ {\mathbf{u}} = - \frac{\varepsilon \zeta }{\mu }{\mathbf{E}}. $$

(6.48)

The Helmholtz-Smoluchowski slip velocity is used as a slip boundary condition to solve the entire flow field for more complicated geometries after solving electrical field. Conventional conditions such as water in silicon microchannel (ε = 6.9 × 10⁻¹⁰ C²/Jm, ζ = −100 mV, μ_water = 10⁻³ Ns/m² and |E| = 1 kV/m) would the slip velocity of ~69 μm/s.

Since the pressure necessary for driving a liquid flow inside a microscale conduit is proportional to the quartic of diameter, electroosmosis is increasingly effective in driving flow as capillary diameter decreases because the flow rate is proportional to the square of diameter in electroosmosis. However, the thin double layer approximation is no longer valid when the electrolyte concentration is extremely diluted or the size of conduit become comparable to the thickness of electrical double layer which has the range of 1–100 nm. The second scenario generally occurs in nanoscale electrokinetics and most of assumption, governing equations and boundary conditions of equilibrium electroosmosis should be modified as non-equilibrium (or the second kind of) electroosmosis.

6.2.4 Nanoscale Electrokinetics

6.2.4.1 Nonlinear Concentration Distribution: Ion Concentration Polarization

Permselective Nanoporous Membrane System

Recently, the ion concentration polarization (ICP) phenomena, which are occurred nearby the nanojunction or nanoporous membrane, have drawn significant attention in a variety of applications such as desalination [13], preconcentration [25], analytical sensors [14], and fuel cells [16]. When the nanochannel is thinner than 100 nm, it has the permselectivity, unique property of nanoscale system, due to the fact that the Debye layer thickness (λ_D) is non-negligible compared with the channel thickness so that the overlap of Debye layer could be happened [24, 26, 27]. Through the permselective nanoporous media, only counter-ion can be transported across the media while co-ion cannot be done. Because of the selectivity of transported species, ion concentration is decrease on one side (this is called ‘depletion’), while on the other side ion concentration is increase (this is called ‘enrichment’) as shown in Fig. 6.3. In other words, the permselectivity is the property, which let only counter-ions pass through the permselective media so that ion concentration is depleted on one side while it is enriched on the other side. The phenomena of concentration polarization front and back of permselective media is called as ICP [28, 29]. As long as the permselectivity of the nanoporous media is stand up, ICP is always occurred nearby the nanojunction.

Fig. 6.3

Schematic diagram of ion concentration distribution nearby permselective media

The permselective systems have a unique feature in the voltage against current curves. As shown in Fig. 6.4a, they have a characteristic shape with a region of slow current variation (the plateau) after a region of linearly increased current against the applied voltage. The linearly increased region is called as ‘Ohmic’ regime and the region of the plateau is called as ‘limiting’ regime. Beyond the limiting regime, the ionic current is grown once again as the applied voltage is increased, this is called as ‘overlimiting’ regime. In the limiting and overlimiting regime, ion depletion zone is extended outward to microchannel reservoir, so that the black region is formed nearby nanoporous membrane shown in Fig. 6.4b. Its extended depletion zone has drawn significant attention in scientific and engineering fields [29,30,31,32].

Fig. 6.4

a Characteristic curves of ionic current against applied voltage of the Ohmic, limiting, and overlimiting regime. b The basic formation of ion-enrichment and ion-depletion in nanofluidic system

In the depletion zone, followings are known as dominant phenomena: (1) ion concentration is depleted below 1/100 dilution against the reservoir concentration [13, 33], (2) the electric field is amplified [34], and (3) strong vortices nearby nanojunction are formed [28]. When the voltage is applied across the cationic permselective nanoporous membrane, cation is permitted to pass through while anion is not. As a result, in cathodic side in microchannel, ions are abundant while ions are depleted below 1/100 times in anodic side. Due to the depletion of ionic species as charge carriers, the electrical conductivity becomes extremely small. Because the ionic current through the system should be uniform, the electric field is amplified in depletion zone to satisfy the uniform ionic current which was confirmed by the experimental measurement [34]. Additionally, strong vortices are formed in the depletion zone to satisfy the continuity condition [28]. The vortex speed was estimated to be usually over 1000 μm/s, which is at least (10) times higher than that of primary electroosmotic flow under the same electric potential. Its speed is proportional to either the square or cube of the applied voltage so that formation of vortex is nonlinear phenomena. At the steady state, Kim et al. [28] clearly observed the counter-rotating vortices adjacent to the nanojunction. In case of single nanojunction, two strong vortices were observed while four independent vortices were formed in the depletion zone of double nanojunctions.

Models for Ion Concentration Polarization

Classical model (derived by Levich in 1962 [35]) based on Nernst-Planck equations, which consider ion transport only due to diffusion and electromigration, predicts the linear concentration profile inside the ion depletion zone and Ohmic/limiting current behavior as a function of applied voltages. In the case of a cation selective membrane, the ionic currents of cation and anion could be expressed as

$$ i_{ + } = - D_{ + } Fz_{ + } \frac{{{\text{d}}c_{ + } }}{{{\text{d}}y}} - \frac{{F^{2} z_{ + }^{2} D_{ + } c_{ + } }}{RT}\frac{{{\text{d}}\psi }}{{{\text{d}}y}} $$

(6.49)

and

$$ i_{ - } = - D_{ - } Fz_{ - } \frac{{{\text{d}}c_{ - } }}{{{\text{d}}y}} - \frac{{F^{2} z_{ - }^{2} D_{ - } c_{ - } }}{RT}\frac{{{\text{d}}\psi }}{{{\text{d}}y}} $$

(6.50)

where i₊ is the ionic current by cation transport, i₋ is the ionic current by anion transport, D₊ is the diffusivity of cation, D₋ is the diffusivity of anion, F is the Faraday constant, z₊ and z₋ is the valence of each ionic species, R is the gas constant, T is the absolute temperature, c₊ and c₋ is the ion concentration of each ionic species, and ψ is the electric potential, respectively. Equations (6.49) and (6.50) are valid in the domain as shown in Fig. 6.5., where the thickness of ICP layer is b.

Fig. 6.5

Schematic diagram of ICP layer for the case of cation selective membrane

In order to analyze the Eqs. (6.49) and (6.50), the condition of electroneutrality is assumed to hold within the fluid; that is,

$$ z_{ + } c_{ + } + z_{ - } c_{ - } = 0 $$

(6.51)

Second assumption is the ideally cation selective membrane. Under second assumption, the anion current must be zero because only cation can pass through the membrane. Its mathematical form is

$$ \left. {i_{ - } } \right|_{y = b} = 0 $$

(6.52)

When there is no anion current source in the fluid, following is hold.

$$ \frac{{{\text{d}}i_{ - } }}{{{\text{d}}y}} = 0 $$

(6.53)

Integrating Eq. (6.53) with respect to y,

$$ i_{ - } = C $$

(6.54)

where C is the integration constant. Due to Eq. (6.52), i₋ should be zero. In next step, the effective concentration is defined by

$$ c = \frac{{c_{ + } }}{{v_{ + } }} = \frac{{c_{ - } }}{{v_{ - } }} $$

(6.55)

where c is the effective concentration, ν₊ and ν₋ are the dissociation number. For example of the dissociation number, ν₊ is 1 and ν₋ is 2 when the electrolyte is CuCl₂. With Eqs. (6.51)–(6.55), (6.49) and (6.50) become

$$ i_{ + } = - D_{ + } Fz_{ + } v_{ + } \frac{{{\text{d}}c}}{{{\text{d}}y}} - \frac{{F^{2} z_{ + }^{2} D_{ + } v_{ + } c}}{RT}\frac{{{\text{d}}\psi }}{{{\text{d}}y}} $$

(6.56)

and

$$ 0 = - D_{ - } Fz_{ - } v_{ - } \frac{{{\text{d}}c}}{{{\text{d}}y}} - \frac{{F^{2} z_{ - }^{2} D_{ - } v_{ - } c}}{RT}\frac{{{\text{d}}\psi }}{{{\text{d}}y}} $$

(6.57)

From the anion current as expressed in Eq. (6.57),

$$ \frac{{{\text{d}}\psi }}{{{\text{d}}y}} = - \frac{RT}{{Fz_{ - } c}}\frac{{{\text{d}}c}}{{{\text{d}}y}} $$

(6.58)

Above expression means that electric migration is same as diffusive transport when the convective transport is negligible. Using Eq. (6.58), the cation current could be reduced in the following form.

$$ i_{ + } = - D_{ + } Fv_{ - } \left( {z_{ + } - z_{ - } } \right)\frac{{{\text{d}}c}}{{{\text{d}}y}} $$

(6.59)

in which the condition of electroneutrality as expressed in Eq. (6.51) is applied in the following modified form.

$$ z_{ + } v_{ + } = z_{ - } v_{ - } $$

(6.60)

Since there is a fixed current for a given applied voltage, it follows that c must be linear in distance across the ICP layer. Consider the case of i₊ > 0 which corresponds to the formation of the depletion. Due to (z₊ – z₋) > 0, (dc/dy) should be negative i.e. the concentration of ions decreases from the ICP layer/bulk interface to the membrane surface. The potential drop is also in the same direction. Integrating Eq. (6.59), concentration profile inside the ICP layer is obtained.

$$ c = c_{0} - \frac{{i_{ + } y}}{{D_{ + } Fv_{ - } \left( {z_{ + } - z_{ - } } \right)}} $$

(6.61)

where c₀ is the bulk concentration. When c|y = b = 0, the current density approaches a limiting value which is called as limiting current.

$$ i_{L} = \frac{{D_{ + } Fv_{ - } \left( {z_{ + } - z_{ - } } \right)c_{0} }}{b} $$

(6.62)

The above limiting current was derived by Levich in 1962. Although Levich’s model pointed out that the bulk charge makes impossible the existence of steady currents greater than the limiting values, Rubinstein and Shtilman [33] showed that this is not true. They showed the increase of the ionic current beyond the limiting regime (plateau of Fig. 6.4a). This regime is called as overlimiting regime. To describe the transition from limiting regime to overlimiting one, some mechanisms have been proposed: (1) bulk charge effect [33], (2) surface conduction along the microchannel wall [31], (3) electro-convective mixing inside the ICP layer [31], and (4) electroosmotic instability [36]. With these mechanisms, depletion zone could be extended toward the reservoir so that system could enter the overlimiting regime. In next, a modified model, which considered above mechanisms, are briefly introduced.

Rubinstein and Shtilman [33] developed the model which allows one to investigate the role of the bulk charge in developing concentration polarization and to trace the connection with classical theory. As the simplest possible model consider a steady current passing through an ideally permselective membrane immersed in a stirred solution of 1:1 valent electrolyte. They assumed that near the membrane there is an ‘unstirred’ layer of thickness δ, which does not depend on the magnitude of the voltage V, applied to this layer. The concentration of the electrolyte is assumed to be constant and equal to c₀. The cation concentration within the membrane is supposed to be equal to the fixed charge concentration N. It is assumed that the ions within the unstirred layer are distributed by means of electro-diffusion only. Direct the x-axis normally to the membrane, identifying x = 0 with the outer boundary of the “unstirred” layer. Then the corresponding boundary value problem takes the form

$$ \frac{{d^{2} \psi }}{{dx^{2} }} = - \frac{4\pi F}{\varepsilon }\left( {c_{1} - c_{2} } \right) $$

(6.63)

$$ \frac{\text{d}}{{{\text{d}}x}}\left( {\frac{{{\text{d}}c_{1} }}{{{\text{d}}x}} + \frac{{Fc_{1} }}{RT}\frac{{{\text{d}}\psi }}{{{\text{d}}x}}} \right) = 0 $$

(6.64)

$$ \frac{\text{d}}{{{\text{d}}x}}\left( {\frac{{{\text{d}}c_{2} }}{{{\text{d}}x}} - \frac{{Fc_{2} }}{RT}\frac{{{\text{d}}\psi }}{{{\text{d}}x}}} \right) = 0 $$

(6.65)

$$ \left. \psi \right|_{x = 0} = 0 $$

(6.66)

$$ \left. {c_{1} } \right|_{x = 0} = \left. {c_{2} } \right|_{x = 0} = c_{0} $$

(6.67)

$$ \left. \psi \right|_{x = \delta } = - V $$

(6.68)

$$ \left. {c_{1} } \right|_{x = \delta } = N $$

(6.69)

$$ \left. {\left( {\frac{{{\text{d}}c_{2} }}{{{\text{d}}x}} - \frac{{Fc_{2} }}{RT}\frac{{{\text{d}}\psi }}{{{\text{d}}x}}} \right)} \right|_{x = \delta } = 0 $$

(6.70)

where ε is the dielectric permittivity. The Poisson equation is represented by Eq. (6.63). The Nernst-Planck equations are represented by Eqs. (6.64) and (6.65), which describe the mass transport of charged species under consideration of the diffusion and the electromigration. Because of assumption of unstirred layer, the Stokes equations and the continuity equation for the fluid flow are not solved. Equations from (6.66) to (6.70) are boundary conditions for unstirred ICP layer. Equations (6.66) and (6.67) are the conditions for bulk reservoir. Equations (6.67)–(6.70) are the conditions for the ideally cation selective membrane, so that anion flux through the membrane surface should be zero. Instead of Eq. (6.68), the Donnan equilibrium is often used, which is the following mathematical form.

$$ \left. \psi \right|_{x = \delta }\,= - V + \frac{RT}{F}\ln \left( {\frac{N}{{c_{0} }}} \right) $$

(6.71)

Due to the Poisson equation, their model could describe the effect of the bulk charge to ICP layer in the overlimiting regime. Their results are showed in Fig. 6.4. In their definition, parameter ε is defined by

$$ \varepsilon = \frac{{\lambda_{D}^{2} }}{{\delta^{2} }} $$

(6.72)

Here the dimensionless parameter has the meaning of a square ratio of the Debye length to the thickness of the unstirred layer. The Levich’s model of concentration polarization, based on the assumption of local electroneutrality corresponds to the limit (Fig. 6.6).

Fig. 6.6

The effect of bulk charge [33]. a Calculated voltage against current curves for different values of parameter, ε. b Calculated ion concentration profiles at different voltages for ε = 10⁻⁴. Solid lines are cation concentration and dashed lines are anion concentration

$$ \varepsilon = 0 $$

(6.73)

With the parameter of Eq. (6.73), ionic current is saturated in the limiting value as denoted in Fig. 6.4a. Due to the effect of the bulk charge, ionic current is increased with different conductance compared with Ohmic regime. In Fig. 6.4b, the plateau of concentration distribution is extended to the bulk interface, in which the plateau is often called as extended space charge layer.

Dydek et al. [31] revisited the classical problem of diffusion-limited ion transport to a membrane by considering the effects of charged sidewalls. Using simple mathematical models and numerical simulations, they identified three additional mechanisms for the overlimiting regime: surface conduction, electro-convective mixing, and electroosmotic instability. In order to consider the effect of the surface conduction only, they assumed that convection becomes negligible compared to diffusion (small Peclet number limit), of which case is corresponding to long, narrow channels and thin double layers. Under their assumption, the Nernst-Planck equations could be homogenized as follows

$$ \frac{{{\text{d}}c_{ + } }}{{{\text{d}}x}} + c_{ + } \frac{{{\text{d}}\tilde{\psi }}}{{{\text{d}}x}} = - \frac{j}{zFD} $$

(6.74)

$$ \frac{{{\text{d}}c_{ - } }}{{{\text{d}}x}} - c_{ - } \frac{{{\text{d}}\tilde{\psi }}}{{{\text{d}}x}} = 0 $$

(6.75)

$$ c = c_{ - } = c_{ + } + \frac{{\rho_{\text{s}} }}{F} $$

(6.76)

where c₊ and c₋ are the mean concentration of cations and anions, respectively, D is the ionic diffusivity, $\tilde{\psi }$ is dimensionless electric potential scaled by the thermal voltage, RT/zF. Equations (6.74) and (6.75) relate the cation flux to the current density j in steady state for an ideally cation selective membrane. Equation (6.76) means averaged electroneutrality condition including both ionic and fixed surface charge of microchannel wall and ρ_s is defined as

$$ \rho_{\text{s}} = \frac{{2\sigma_{\text{s}} }}{H} $$

(6.77)

where σ_s is the surface charge density of microchannel wall and H is the depth of the microchannel. Without the loss of generality, they could be derived analytical solutions of Eqs. (6.74) and (6.75). The current-voltage relation is demonstrated to possess nearly constant conductance in the overlimiting regime. Also, the plateau of the concentration profile is formed as similar as the extended space charge layer of Rubinstein and Shtilman [33]. Additionally, they considered the effect of electro-convective mixing. Under and assumption of dead-end channel, pressure-driven back flow opposes electroosmotic flow and results in two counter-rotating vortices. Concentrated solution flows to the membrane along the sidewalls, and depleted solution returns in the center. To describe the electro-convective mixing, they assumed thin double layers and neutral bulk solution described by the steady 2D Nernst-Planck equations, the Stokes equations, and the continuity equation. These governing equations with appropriate boundary conditions were solved numerically. As a result, numerical solutions to describe the electro-convective mixing were obtained.

These coupled phenomena resembled the ion transportation through cell membrane since the membrane has various-sized nanopore so that effective control of important ions such as Na⁺ and K⁺ are regulated by this basic transport phenomena. In next, we will introduce more intense mechanism called ionic field effect transistor that is capable of controlling the ion transportation through the nanoporous membrane.

6.2.4.2 Modulated Ion Transportation: Ionic Field Effect Transistor

Ionic Field Effect Transistor: Voltage-Gated Nanoscale System

Recent advances in nano-fabrication methods enable to fabricate rigorous and definite nano-sized structure for various scientific and engineering applications. Nanostructure possesses unique scientific and technological properties that microstructure cannot exhibit. Especially, as decreasing the size of nanostructure below 100 nm, the structure had a perm-selectivity which let only counter-ions can pass through below a critical electrolyte concentration. The perm-selectivity was reported to be depending on the magnitude and polarity of surface charge density and bulk electrolyte concentration. Thus, the active control of the surface charge density at wide range of electrolyte concentration has been drawn significant attentions in both scientific and engineering field [15, 37,38,39,40,41] for manipulating the motion of charged species and this has become one of the important fields in nanofluidics research. The emerging application fields of nanofluidic system were energy harvesting [15, 37], biosensors [38, 39], backflow from shale gas extraction port [40] or desalinations of seawater [41] which enable to create a huge market that never have existed. Those applications were fundamentally originated from controlling the motion of charged species passing through a nanostructure and, therefore, the cost-effective/on-demand/sensitive control has become the most important practical issue of nanofluidic researches.

Various passive types of modulating the motion of a charged species in nanofluidic system were reported such as changing the viscosity of solution in the nanochannel [42], utilizing mechanical friction between DNA and nanopore [43], coating an adhesive material on nanochannel [44] and surface treatment for changing the surface potential [12, 45]. Those platforms employed passive methods which were unable to change the behavior of charged species on-demand, once the devices were fabricated. In contrast, ionic field effect transistor (IFET) can provide an active method which enables to enhance, diminish or even reverse the behavior of charged species in situ by introducing gate potential.

Figure 6.5a shows a schematic of metal-oxide-electrolyte system which is a key-building unit of ionic field effect transistor. When voltage is applied to the metal part called as gate electrode, surface potential on oxide-electrolyte interface is modulated by field effect so that the electric double layer (EDL) inside the electrolyte solution is changed depending on the applied voltage on the gate electrode. This process is how the IFET control the ionic transport in the nanoscale system. The metal-oxide-electrolyte system is integrated on nanochannel wall, then the nanochannel is connected with microchannel. Figure 6.5b shows the schematic of typical ionic field effect transistor.

The first experimental results of an ionic field effect transistor were demonstrated by Gajar and Geis [46] in 1992. The devices had nanochannels about 88 nm in height and 300–900 μm in length. They investigated both the steady-state and transient responses of their ionic FET devices. However, it was found that the response of the IFET to a step voltage in the gate terminal is quite slow. This is mainly due to two reasons. The first is the large geometries of the nanochannel and the second is the existence of processes other than ambipolar diffusion.

In 2004, theoretical modeling of the ionic transport in silica nanotubes revived research interest in IFET devices [45]. Fan et al. [47] experimentally demonstrated field effect modulation of ion transport using gated silica nanotubes shown. Using KCl as the testing solution, they found that as the gate voltage varies from −20 to +20 V, the ionic conductance decreases monotonically from 105 pS down to 45 pS, due to depletion of cations under the applied electric field, which shows a typical p-type transistor behavior. Since then, various IFET have been reported. Using multiple nanopore structures with sub-10 nm diameters and TiO₂ as dielectric material, Nam et al. [18] also showed that the ionic conductivity of the nanopore can be modulated by a gating voltage. A p-type I–V characteristic was also observed, which suggested the major carriers are cations.

Another application is the control of single molecule translocating through the nanoscale system. Since biomolecules usually have multivalent charges, field effect control over the molecule transport in nanochannels can be more effective than monovalent ions. It has been experimentally observed that the fluorescence intensity of 30-base fluorescently labeled single-stranded DNA (ssDNA) in a 1 mM KCl solution could be increased by six times in 2D nanoslits, which is ascribed by the electrostatic interactions between the gating voltage and DNA molecules [48]. It is found that both electroosmotic flow (EOF) and electrostatic interactions arising from the field effect control can effectively regulate the DNA translocation through a nanopore. Recently, Paik et al. [49] demonstrated a gated nanopore structure that is capable of reversibly altering the rate of DNA capture by over three orders of magnitude. They ascribed this extremely large modulation ratio to the counterbalance between the electrophoresis (EP) and the EOF, rather than pure electrostatic interactions between the gating voltage and the DNA molecules. When the gating voltage was low, EOF overwhelmed the EP. Thus DNAs were rejected from entering the pore. In contrast, a high gating voltage reduced the EOF due to the reduced Na+ in the diffuse layer of the nanopore wall so that DNAs were accepted to pass through the nanopore.

To reflect these complex features, widely-used models to describe the electrokinetic phenomena inside the IFET will be discussed in the next section.

Conventional Models for Ionic Field Effect Transistor

In this section, descriptions of the complete set of equations that were used for simulation of electrokinetic transport in IFET are presented. Most models were formulated under Poisson-Nernst-Planck-Stokes coupled governing equations with appropriate boundary conditions shown in Sect. 6.2.2. Gate effects on ionic transport were interpreted as boundary conditions so that the independent differential equations should be needed. Firstly, general governing equations and boundary conditions are rewritten for the metal-oxide-electrolyte system. Secondly, the gate modulated is described by the Poisson-Boltzmann equation and the Laplace equation.

As discussed in Sect. 6.2.4, the Poisson-Nernst-Planck-Stokes (PNPS) equations are used to describe the nanoscale electrokinetic system. The electrostatic potential ψ is governed by the Poisson equation

$$ \nabla \cdot (\varepsilon \nabla \psi ) = - \rho_{\text{f}} $$

(6.78)

where meaning of parameter was discussed in Sect. 6.2.1. In Eq. (6.49), the volume charge density is represented by

$$ \rho_{\text{f}} = F\sum\limits_{i} {z_{i} } c_{i} $$

(6.79)

c_i in the above equation is provided by the Nernst-Planck equations, which combines the diffusion due to a concentration gradient, the migration due to an electric field, and convection due to a ambient flow field.

$$ \nabla \cdot {\mathbf{J}}_{i} = \nabla \cdot \left( { - D_{i} \nabla c_{i} - \frac{{z_{i} FD_{i} }}{RT}c_{i} \nabla \psi + c_{i} {\mathbf{u}}} \right) = 0 $$

(6.80)

without any chemical reactions. To obtain solutions for flow field, the Stokes equations and the continuity equation should be solved by coupling manner.

$$ {\mathbf{0}} = - \nabla p + \eta \nabla^{2} {\mathbf{u}} - \rho_{\text{f}} \nabla \psi $$

(6.81)

$$ \nabla \cdot {\mathbf{u}} = 0 $$

(6.82)

With above governing equations from (6.78) to (6.82), appropriate boundary conditions should be determined. The numerical domain for conventional IFET is shown in Fig. 6.5b. Numerical boundaries were divided into four sections: (1) axis of symmetry, (2) inlet/outlet, (3) reservoirs, and (4) nanochannel wall, as denoted in Fig. 6.5b. Dash-dot line represents axis of symmetry in the cylindrical coordinate system, thus this boundary (denoted as ‘(1)’) possessed symmetry conditions. Corresponding mathematical forms about the axis of symmetry are

$$ {\mathbf{n}} \cdot \nabla \psi = 0 $$

(6.83)

$$ {\mathbf{n}} \cdot {\mathbf{j}}_{i} = 0 $$

(6.84)

$$ {\mathbf{n}} \cdot {\mathbf{u}} = 0 $$

(6.85)

In the above conditions, n is the outward normal vector. On the inlet/outlet boundaries of nanoscale system (denoted as ‘(2)’), electric potential, concentration and pressure were fixed at specific values.

$$ \psi = 0\left( {\text{source}} \right) $$

(6.86)

$$ \psi = V_{\text{D}} ({\text{drain}}) $$

(6.87)

$$ c_{i} = c_{0} $$

(6.88)

$$ p = 0 $$

(6.89)

where V_D is the applied voltage on drain electrode and c₀ is the bulk electrolyte concentration. The third boundary type is reservoirs (denoted as ‘(3)’) on which insulating conditions were satisfied.

$$ {\mathbf{n}} \cdot \nabla \psi = 0 $$

(6.90)

$$ {\mathbf{n}} \cdot {\mathbf{j}}_{i} = 0 $$

(6.91)

$$ {\mathbf{n}} \cdot {\mathbf{u}} = 0 $$

(6.92)

Note that these mathematical forms are equal to conditions of the axis of symmetry, but their physical meanings are different. Most importantly, last boundary type is nanochannel wall (denoted as ‘(4)’) on which surface charge density was set up by normal derivative of electric potential and the walls had no-penetration condition and no-slip condition for the Nernst-Planck equations and the Stokes equations, respectively.

$$ - \varepsilon \,{\mathbf{n}} \cdot \nabla \psi = \sigma_{\text{s}} $$

(6.93)

$$ {\mathbf{n}} \cdot {\mathbf{j}}_{i} = 0 $$

(6.94)

$$ {\mathbf{u}} = {\mathbf{0}} $$

(6.95)

where σ_s is the surface charge density on the nanochannel wall. The detailed expressions of boundary conditions were summarized in Table 6.2 once more.

Table 6.2 Boundary conditions for each equation of the model

As earlier mentioned, IFET could be modeled as metal-oxide-electrolyte (MOE) system. In the usual MOE system, the surface charge density modulated by gate voltage is obtained from simple algebraic equations independent of governing equations. The MOE structure depicted in Fig. 6.7a can be naturally incorporated into chip-based fluidic devices to perform electro-fluidic gating. Its geometry is that of a parallel-plate capacitor as denoted in Fig. 6.8. whose metallic gate electrode is separated from the conductive electrolyte by a thin insulating oxide. The electric double layer is modulated by applying a voltage across the capacitor, which generates an electric field normal to the solid-liquid interface. Here we introduce models for the charging behavior of the MOE capacitor. The electric double layer screens electric fields, whether they originate from the chemical charge at the oxide surface or from the applied voltage across the capacitor. To treat these two contributions separately, we consider an equivalent circuit model of the MOE capacitor, shown in Fig. 6.8. This simple model allows us to determine the potential and the charge density at every location. It consists of three elements arranged in series: two linear capacitors representing the oxide and the Stern layer and a nonlinear element representing the electric double layer. The potential difference across the oxide layer is V_G − ψ_s. The oxide is assumed to have a constant capacitance per unit area, C_ox, that accurately describes the dielectric properties of common materials used in micro- and nanofluidic devices such as silicon dioxide (SiO₂), aluminum dioxide (Al₂O₃), and poly-dimethylsiloxane (PDMS) [50,51,52]. The capacitive charge density induced at the surface of the insulator, σ_ox, is given by

Fig. 6.7

a Schematic of metal-oxide-electrolyte system which is a key-building structure of ionic field effect transistor. b Schematic of gated nanochannel connected with microchannel reservoir. This structure is called as ionic field effect transistor

Fig. 6.8

Equivalent circuit model of the MOE capacitor. The oxide layer are modeled as capacitors of specific capacitance C_ox and C_Stern, respectively

$$ \sigma_{\text{ox}} = C_{\text{ox}} \left( {V_{\text{G}} - \psi_{\text{s}} } \right) $$

(6.96)

Within the basic Stern model, the potential drops linearly across the solid-liquid interface by an amount ψ_s − ζ. The relationship between this potential drop and the charge density screened by the double layer, σ_DL, is given by

$$ \sigma_{\text{DL}} = C_{\text{Stern}} \left( {\psi_{\text{s}} - \zeta } \right) $$

(6.97)

where C_Stern is the phenomenological Stern capacitance per unit area. C_Stern reflects the structure and dielectric properties of the solid-liquid interface. The basic Stern model has been widely applied to model the charging of the double layer and is well supported by experimental evidence [53,54,55]. When the surface reactions between functional groups on the oxide layer and ionic species in the electrolyte solution is considered, the net charge density on the surface of the oxide layer must equal the chemical charge density from the ionized surface groups charge density from the ionized surface groups, σ_chem; therefore,

$$ \sigma_{\text{chem}} = \sigma_{\text{DL}} - \sigma_{\text{ox}} $$

(6.98)

However, in most cases, the Stern layer and chemistry of the oxide/electrolyte interface are neglected [56, 57] so that σ_chem is zero, and then remaining surface charge densities become

$$ \sigma_{\text{DL}} = \frac{2\varepsilon \kappa RT}{F}\sinh \left( {\frac{F}{2RT}\left( {\zeta - V_{\text{b}} } \right)} \right) $$

(6.99)

and

$$ \sigma_{\text{ox}} = C_{\text{ox}} \left( {V_{\text{G}} - \zeta } \right) $$

(6.100)

Therefore, gate modulated zeta potential can be determined by Eqs. (6.21)–(6.23) when the Stern layer and the surface reaction are neglected.

6.2.5 Concluding Remarks

Over the past decade, microfluidic and nanofluidic applications have drawn to significant attentions in science and engineering fields. Although the conventional theory well-described the microscale system, additional constraints to describe the nanoscale system should be necessary. However, these additional constraints could not be found by only experimental manner because observation inside the nanoscale system was impossible. In this chapter, we introduced microscale electrokinetics which started from the basic conservation laws and then, focused on two nanoscale electrokinetic phenomena occurs near (or through) a permselective nanoporous system; (1) ion concentration polarization and (2) ionic field effect transistor. They are closely related to the unique ion transportation for direct ion separation or selective ion transportation inside human body or cell-cell environments. Conclusively, due to the difficulties of direct observation inside these nanoscale system, the theoretical formulation with nonlinear constraints would be one of the possible manners to investigate the nanoscale system.

6.3 Electrostatics for Biodevices: Dielectrophoresis (Marie Frenea-Robin, Bruno Le Pioufle)

In this section, the effect of dielectrophoretic forces on cells is examined. Dielectrophoresis arises from the interaction between a polarized particle and a non-uniform electric field in which the particle is immersed. In the case where a stationary electric field is applied, living cells polarize and move towards field minima or maxima, depending on their polarization contrast with the medium. This contrast is characterized by the Clausius-Mossotti factor ${\text{f}}_{\text{CM}}$, which is a function of the complex permittivities of both cell and medium. This principle, referred to as conventional dielectrophoresis (cDEP) is commonly used for cell sorting or cell trapping, as will be illustrated with some examples found in the literature. Propagative electric fields are also often used to apply dielectrophoretic forces, which corresponds to travelling wave dielectrophoresis (tw-DEP) in the case of linear propagation, or electrorotation (E ROT), when a rotational electric field is considered. Applications where these two other forms of dielectrophoresis are implemented will also be reported in this chapter. Lastly, examples regarding DEP of biomolecules will be briefly reviewed.

6.3.1 Introduction, Basics of the Dielectrophoresis Phenomenon

This section introduces the basics of dielectrophoresis, from the interaction between an electric field and a polarized particle, up to the generalized formula of the DEP force.

6.3.1.1 Dielectrophoretic Force Induced on a Spherical Particle

A spherical particle (radius $R$, complex permittivity $\varepsilon_{p}^{*}$) get polarized once exposed to an external electric field $\vec{E}$. The particle behaves as an electrostatic dipole $\vec{m}$ which is a function of the sphere radius $R$ and of the complex permittivities of both particle and medium (respectively $\varepsilon_{p}^{*}$ and $\varepsilon_{m}^{*}$, that appear in the proportional dependency to the Clausius Mossotti factor $f_{CM} = \frac{{\varepsilon_{p}^{*} \, - \,\varepsilon_{m}^{*} }}{{\varepsilon_{p}^{*} \, + \,2\varepsilon_{m}^{*} }}$):

$$ \vec{m} = 4\pi \varepsilon_{m} f_{CM} \vec{E} $$

(6.101)

where the complex permittivity $\varepsilon^{ *}$ defined in Eq. 6.102 depends on the permittivity $\varepsilon$ and conductivity of the particle and medium:

$$ \varepsilon^{ *} = \varepsilon - i\frac{\sigma }{\omega } $$

(6.102)

and i is the complex number ($i^{2} = - 1$).

This electrostatic dipole interacts with the external electric field, and experiences the dielectrophoretic force:

$$ \overrightarrow {{F_{DEP} }} = \left( {\vec{m}.\vec{\nabla }} \right)\vec{E} $$

(6.103)

where $\vec{\nabla }$ is the space derivative vector $\vec{\nabla } = \left( {\frac{\partial }{\partial x} \frac{\partial }{\partial y} \frac{\partial }{\partial z}} \right)^{t}$

In the case where the electric field varies sinusoidally with the time:

$$ \vec{E} = E_{xo} \cos \left( {\omega t + \varphi_{x} } \right)\vec{x} + E_{yo} \cos \left( {\omega t + \varphi_{y} } \right)\vec{y} + E_{zo} \cos \left( {\omega t + \varphi_{z} } \right)\vec{z} $$

(6.104)

$\omega$ being the angular frequency of the applied field, and $\vec{x}$, $\vec{y}$, $\vec{z}$ are the unitary vectors of the Euclidean space. $\varphi_{x}$, $\varphi_{y}$, $\varphi_{z}$, $E_{xo} , E_{yo} , E_{zo}$ are respectively the phase shifts and field modulus on the $\vec{x}$, $\vec{y}$, $\vec{z}$ directions.

The dielectrophoresis force then expresses as follows:

$$ \overrightarrow {{F_{dep} }} = 2\pi \varepsilon_{m} R_{cell}^{3} {\Re }\left( {f_{CM} } \right)\overrightarrow {{\nabla E^{2} }} + 2\pi \varepsilon_{m} R_{cell}^{3} {\Im }\left( {f_{CM} } \right)\left( {E_{xo}^{2} \overrightarrow {{\nabla \varphi_{x} }} + E_{yo}^{2} \overrightarrow {{\nabla \varphi_{y} }} + E_{zo}^{2} \overrightarrow {{\nabla \varphi_{z} }} } \right) $$

(6.105)

6.3.1.2 Case of Cells

In the case of cells, the dielectrophoretic force direction and amplitude thus depend on the Clausius-Mossotti factor f_CM which is a function of the difference of complex permittivities between the cell and the medium [58]:

$$ f_{CM} = \frac{{\varepsilon_{cell}^{ *} - \varepsilon_{m}^{ *} }}{{\varepsilon_{cell}^{ *} + 2\varepsilon_{m}^{ *} }} $$

(6.106)

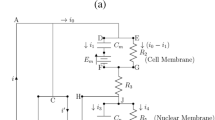
The complex permittivity of a spherical shaped cell is commonly simplified to an approximated value $\varepsilon_{cell}^{*}$ obtained thanks to the Single shell model [59]. This model describes the cell as an averaged inner compartment (which dielectric properties are $\sigma_{in}$ and $\varepsilon_{in}$), surrounded by an outer cytoplasmic membrane (dielectric properties $\sigma_{memb}$ and $\varepsilon_{memb}$, radius $R_{cell}$, thickness e, see Fig. 6.9):

Fig. 6.9

Single shell model of the cell. The cell is composed of an averaged intra-cellular compartment (defined by its permittivity $\upvarepsilon_{\text{in}}$, its conductivity $\upsigma_{\text{in}}$ and radius ${\text{R}}_{\text{cell}}$), surrounded by the cell membrane (permittivity $\upvarepsilon_{\text{memb}}$, conductivity $\upsigma_{\text{memb}}$ and thickness e)

$$ \varepsilon_{cell}^{ *} = \varepsilon_{memb}^{ *} \left[ {\frac{{\left( {\frac{{R_{cell} }}{{R_{cell} \, - \,e}}} \right)^{3} + 2\left( {\frac{{\varepsilon_{in}^{ *} \, - \,\varepsilon_{memb}^{ *} }}{{\varepsilon_{in}^{ *} \, + \,2\varepsilon_{memb}^{ *} }}} \right)}}{{\left( {\frac{{R_{cell} }}{{R_{cell} \, - \,e}}} \right)^{3} - \left( {\frac{{\varepsilon_{in}^{ *} \, - \,\varepsilon_{memb}^{ *} }}{{\varepsilon_{in}^{ *} \, + \,2\varepsilon_{memb}^{ *} }}} \right)}}} \right] $$

(6.107)

6.3.2 Using Dielectrophoresis to Induce Translational Motion

6.3.2.1 Handling Cells Using a Stationary Electric Field

The phenomenon described in this section, arising in the presence of a stationary field, is sometimes referred to as ‘conventional dielectrophoresis’ (cDEP). In electric fields with constant phase, Eq. 6.105 giving the time-averaged force acting on a cell simplifies to:

$$ \overrightarrow {{F_{dep} }} = 2\pi \varepsilon_{m} R_{cell}^{3} {\Re }\left( {f_{CM} } \right)\overrightarrow {{\nabla E_{RMS}^{2} }} $$

(6.108)

This equation indicates that the DEP force intensity is cell-volume dependent and that the force cancels if the field is uniform ($\overrightarrow {{\nabla E_{RMS}^{2} }} = 0$, where $E_{RMS}$ denotes the root-mean-square electric field). The DEP force varies with the square of the applied field magnitude, and its direction is therefore not affected by the field polarity. It is due to the fact that a field reversal results in a reversed induced dipole moment. It also implies that both direct current (DC) and alternating current (AC) can be used. Dielectrophoresis should therefore not be confused with electrophoresis, which refers to the motion of charged particles in DC electric fields.

It can be seen from Eq. 6.108 that the direction of the force depends on the sign of the real part of the $f_{CM}$ factor. The case where ${\Re }\left( {f_{CM} } \right) > 0$ corresponds to the cell being more polarisable than its surrounding medium, resulting in an induced dipole moment aligned with the applied field. As a consequence, the cell is translated towards regions of highest electric field magnitude under the effect of positive DEP (pDEP, see Fig. 6.10a). Conversely, the case where ${\Re }\left( {f_{CM} } \right) < 0$ corresponds to the cell being less polarisable than its immersion medium, resulting in an induced dipole moment directed against the applied field. The cell is then directed towards areas of low electric field strength, which is referred to as negative DEP (nDEP, see Fig. 6.10b).

Fig. 6.10

Illustration of conventional DEP principle. a. pDEP arises when the cell is more polarisable than its immersion medium. Due to the non-uniform character of the field, a different electric force is induced on the two poles of the net effective dipole. This results in a translation of the cell towards the region of high electric field strength. b. nDEP corresponds to the case where the induced dipole opposes the applied field. Due to the force imbalance, the cell is now pushed down the gradient, from higher to lower field intensities. It should be noted that the direction of motion remains unchanged when the electrode polarity is reversed

For a spherical particle, the real part of the $f_{CM}$ factor is comprised between −0.5 and 1. This term therefore not only determines the direction of the force, but it also affects its intensity. As can be seen from Fig. 6.11, the dielectrophoretic behaviour of a cell can be adjusted by tuning the field frequency. It should be noted that the conductivity and permittivity of the cell themselves vary with the frequency, due to the heterogeneous structure of biological particles (Fig. 6.12). In the low frequency range (below a few tens of kHz), the DEP force depends on the respective conductivities of the cell and its immersion medium. The cell membrane blocks current flow, which leads to the cell being less polarizable than the medium (i.e. nDEP force). With increasing frequency, the high membrane resistance is progressively bypassed by the membrane capacitance, and the magnitude and direction of the force depend on the interplay between the dielectric properties of the membrane and cytoplasm. At frequencies higher than a few tens of MHz, the DEP response is dominated by the respective permittivities of cell interior and surrounding medium.

Fig. 6.11

Plot of the DEP response of a Jurkat cell (human T lymphocyte) for three different values of the medium conductivity. The shape of the curves is typical for a living cell with intact membrane. The following values were introduced in Eq. 6.107 [60]: $\sigma_{memb} = 3\; \times \;10^{ - 6}\,{\text{S}} \cdot {\text{m}}^{ - 1}$; $\varepsilon_{memb} = 6*\varepsilon_{0} \;{\text{F}} \cdot {\text{m}}^{ - 1}$; $\sigma_{in} = 0.4\;{\text{S}} \cdot {\text{m}}^{ - 1}$; $\varepsilon_{in} = 45*\varepsilon_{0} \,{\text{F}} \cdot {\text{m}}^{ - 1}$; $R_{cell} = 5$ μm; $e = 5 \,{\text{nm}}$

Fig. 6.12

Evolution of cell effective conductivity and permittivity with respect to frequency (from Eq. 6.107)

As can be seen on Fig. 6.11. There are two frequencies at which the direction of the DEP force exerted on the cell reverses, commonly referred to as “crossover frequencies”.

The lower crossover frequency value, corresponding to a transition from nDEP to pDEP, can be shifted by modifying the surrounding medium conductivity. Hence this parameter plays an important role on the cell dielectrophoretic behaviour. Low conductive media ($\upsigma_{\text{m}}$ being a few tens of mS · m⁻¹) are currently used in DEP experiments because in more conductive physiological media ($\upsigma_{\text{m}} \approx 1\;{\text{S}} \cdot {\text{m}}^{ - 1}$) observation of pDEP is only possible at very high frequencies and Joule heating effects can become a concern. The low conductivity buffer used must be formulated to maintain pH and osmolarity within the physiological range.

As previously mentioned, the force intensity is directly proportional to the gradient of the squared electric field strength. If the electrode gap is scaled down by a factor K, the DEP force gets scaled up by a factor of $K^{3}$. Hence significant forces can be generated by applying a few volts to miniaturized electrodes. The electric field distribution is determined by the choice of the electrode geometry. The spatial non-uniformities required for the DEP effect is commonly generated by 2D co-planar electrodes of interdigitated, castellated or polynomial design [61]. Yet, a variety of alternative electrode structures have also been developed to allow exploitation of interesting 3D effects, such as “top-bottom” electrodes [62] or sidewall conducting PDMS electrodes in microfluidic devices [63, 64]. Insulating structures in a microchannel with remote electrodes can also be exploited to shape the electric field [65], following the principle of IDEP (insulator-based dielectrophoresis). Demierre et al. proposed the concept of “liquid electrodes” combining planar electrodes with IDEP technique [66]. This configuration exploits metal electrodes fabricated on the bottom of dead-end chambers placed on the side of a microfluidic channel and acting similarly to thick electrodes embedded in the channel walls. Detailed reviews of microfabrication technologies and microelectrode geometries employed in DEP applications can be found in the literature [67, 68].

Dielectrophoresis is a technique currently employed for cell handling in microfluidic systems. As a contactless and label-free manipulation method, it provides a non invasive tool to perform various tasks such as sample preparation (concentration, filtering, enrichment), cell sorting or cell isolation prior to further detection or measure of response to various stimuli. DEP has been used for instance in immunosensors to enhance the capture and detection of pathogenic bacteria by bringing the cells to the sensor site while increasing the contact between the target and the immobilized antibodies, prior to sandwich ELISA detection of captured cells [69]. Hamada and coworkers proposed similarly to detect bacteria by first capturing cells onto microelectrodes using pDEP and then measuring the variation of electrode impedance due to the presence of trapped bacteria [70].

DEP traps were also designed to perform parallel single-cell assays. Monitoring of many individual cells at the same time involves their patterning in array format, which can be achieved using quadrupole electrode units [71,72,73]. This electrode arrangement offers the advantage of providing strong confinement under nDEP, as cells less polarizable than the surrounding suspending medium will be directed away from electrode edges towards the center of the interelectrode gap [61]. Silicon Biosystems has developed and brought to market a chip called DEPArray^TM for massively parallel handling of cells with single cell resolution. Programmable electrodes are used to generate DEP “cages” within which single cells may be trapped, levitated and manipulated individually. A DEP cage corresponds to a field minimum created above a microelectrode by applying a sinusoidal voltage to the associated electrode and to the conductive Indium Tin Oxide (ITO) lid, and a counterphase sinusoidal voltage to the surrounding electrodes. The dynamic traps can be reconfigured dynamically under software control, so as to move the cells above the device plane towards the desired target location.

DEP-driven cell assembly also constitutes a promising route to engineer biomaterials that mimic the structure of native tissues and develop cell-culture platforms reproducing in vivo cellular microenvironment. Ho et al. have demonstrated rapid heterogeneous patterning of liver cells using concentric radiating tip electrode array. The obtained alternate radial pattern of hepatocytes and endothelial cells mimicked the lobular morphology of real liver tissue [74]. Such bottom-up approach may provide better control over the relative spatial organization of cells compared to more traditional top-down approaches based on scaffolds. It also offers the advantage to promote cell-cell interactions. Menad et al. have recently shown that cell aggregates of regular size and shape could be fabricated using nDEP. Those cell assemblies could be maintained by cell-cell adhesion after the electric field removal and indications of cell activity into aggregates were observed after overnight incubation [75]. This may offer a new approach to produce 3D tumor spheroid models for in vitro therapeutic screening.

One of the main applications of dielectrophoresis is the selective capture of target cells from a mixed population, which can be achieved without the need for labeling. Since dielectric properties of cells are dependent upon various parameters including morphological factors such as cell volume and membrane area, different cell types will exhibit different crossover frequencies in a given medium.

The simplest separation approach consists in dividing a cell mixture into two distinct sub-populations, by choosing an operating frequency at which one fraction of cells is submitted to nDEP and the other one to pDEP. Physical separation of the two sub-populations is then achieved by superimposing a liquid flow above the electrode array. Based on this principle, Becker et al. have shown that human breast cancer cells could be separated from blood using the castellated electrode design described on Fig. 6.13a [76].

Fig. 6.13

a. Illustration of DEP cell separation for a mixture containing two cell subpopulations. The field frequency $f$ is chosen so as to fall between the DEP crossover frequencies of the two cell types $f_{c1}$ and $f_{c2}$. Red cells exposed to positive DEP are trapped at the electrode tips, while blue cells experiencing nDEP are focused into bands and carried away by the fluid stream. b. Side view of a DEP-FFF separation chamber. Cells of type 1 and 2 submitted to nDEP are levitated at two different heights $h_{1}$ and $h_{2}$ above the electrode array placed at the chamber floor. Since they are closest to the middle of the channel height, blue cells move at a faster velocity $\left( {v_{1} > v_{2} } \right)$ and reach the device output first

Doh and Cho presented a continuous cell separation chip using three planar electrodes placed at the bottom of a microfluidic channel. Cells with pDEP affinity moved towards the chamber walls while cells with nDEP affinity remained in the central streamline. The laminar nature of the flow enabled the collection of cell fractions through different outlets [77]. Bisceglia et al. developed a method and a microfluidic device for the extraction and concentration of pathogens from a suspension of blood cells, based on the large tolerance of micro-organisms towards osmotic shocks. A hypotonic medium selectively alters blood cells and changes their dielectric properties while keeping most micro-organisms functional. Following this approach, micro-organisms were trapped using pDEP, while altered blood cells submitted to negative dielectrophoresis were driven by the flow towards the device outlet [78].

Cell separation can also be achieved using dielectrophoresis field flow fractionation (DEP-FFF), a chromatographic approach in which cells are positioned at different heights within the separation chamber using a combination of dielectrophoretic and sedimentation forces. Due to the parabolic flow profile, different cell subpopulations travel at different velocities according to their distance from the chamber floor and therefore emerge from the outlet at different times (Fig. 6.13b). Provided the chamber length is long enough, this method allows to fractionate cells with subtle differences. It also enables to discriminate more than two cell classes. A continuous flow microfluidic processing chamber was recently proposed by Gascoyne and coworkers to achieve a throughput as high as 10⁶ cells ∙ min⁻¹ and isolate circulating tumor cells from 10 mL clinical blood specimens in less than 1 h [79]. The ApoStream® technology developed by ApoCell Inc is based on this approach.

6.3.2.2 Handling Cells Using a Propagative Electric Field

The second term of Eq. 6.105 is related to the twDEP force acting on a spherical particle. This term exists only in non-uniform electric fields with spatially dependent phase and if the imaginary component of the Clausius Mossoti factor is not null. A travelling field can be generated using sequentially phase-shifted AC voltages applied to an array of finger electrodes (see Fig. 6.14). The resulting translational force propels the particle along the electrodes, with or against the field direction, depending on whether the imaginary component of the Clausius Mossoti factor is negative or positive, respectively. In practice the operating conditions (field frequency, medium conductivity) are chosen so as to meet the following requirements: (i) cells must be repelled from the electrode array by nDEP $\left( {{\Re }\left( {f_{CM} } \right) < 0} \right)$, rather than trapped on the electrodes by pDEP and (ii) ${\Im }\left( {f_{CM} } \right) \ne 0$.

Fig. 6.14

Illustration of twDEP principle. In the frequency range delimited by the grey band (see DEP cell spectra on the right), cells are levitated by nDEP above the electrode array $\left( {{\Re }\left( {f_{CM} } \right) < 0} \right)$ to a height at which $F_{cDEP}$ and the sedimentation force $F_{g}$ balance. Due to the $F_{twDEP}$ force component, cells are also translated along the electrodes against the travelling field direction $\left( {{\Im }\left( {f_{CM} } \right) > 0} \right)$, at a velocity limited by Stokes drag

twDEP is also employed in spiral cell concentrators: using parallel spiral electrodes excited with phase-shifted signals enables to produce a force acting along the radial direction and to collect cells of interest at the centre of the device. This principle was exploited by Gascoyne and coworkers for detecting malaria in blood samples by DEP. Application of four phase signals to the spiral electrode array caused normal erythrocytes to be trapped at the electrode edges by pDEP while parasitised cells were levitated and carried towards the centre of the spiral by the travelling field [80]. Van Den Driesche et al. developed a continuous cell separation device comprising a finger electrode array placed at the bottom of the microfluidic channel so as to produce a travelling electric field perpendicular to the pressure driven flow. Jurkat cells and Lactobacillus casei bacteria present in the input sample responded differently to the transverse twDEP force. At a given frequency, only Jurkat cells were deflected from their initial flow path, which enabled to collect them at the opposite side of the separation chamber [81].

6.3.3 Using Rotating Fields to Induce Electrorotation

This section describes how the cell dielectric parameters can be estimated through its electromechanical response when immersed in a rotary propagative electric field. In an electrorotation experiment, the angular frequency of the electric field is varied in order to produce a cell mechanical velocity spectrum. The resulting spectrum is highly informative on the cell components properties.

6.3.3.1 Extraction of the Cell Dielectric Parameters from an Electrorotation Experiment—Principle

Once immersed within a rotational electric field, the cell experiences a torque, which direction $\vec{z}$ is normal to the electrode plan. This phenomenon, named electrorotation, is due to a phase lag between the field and induced dipole moment.

$$ \overrightarrow {{\Gamma _{dep} }} = \vec{m} \otimes \vec{E} = - 4\pi R^{3} \varepsilon_{m} {\Im }\left( {f_{CM} } \right)E^{2} \vec{z} $$

(6.109)

The cell consequently rotates, with a rotational velocity $\Omega _{cell}$ that depends on the angular frequency of the electric field. The steady-state electrorotation rate corresponds to the speed at which the torque and the hydrodynamic friction balance. A spectrum of the rotational velocity can thus be measured:

$$ \Omega _{cell} \left( \omega \right) = \frac{{\varepsilon_{0} \varepsilon_{m} E^{2} }}{2\eta }{\Im }\left( {f_{CM} } \right) $$

(6.110)

where $\eta$ represents the dynamic viscosity of the medium.

The mechanical velocity is dependent on the cell dielectric parameters (complex permittivities of the membrane and of the cell content) that can thus be estimated. To do so, the distance between the measured spectrum of the rotational velocity of the cell $\Omega _{cell} \left( \omega \right)$ and the theoretical one, which is a function of the complex permittivities of its different domains (Eqs. 6.110, 6.106 and 6.107 in the case of a cell modeled by the single shell), is minimized thanks to least square algorithm [82].

6.3.3.2 Using Octupole Electrodes to Levitate the Cell

When conducting an electrorotation experiment, a common strategy consists in first trapping the cell using a four-electrode set, by applying a stationary electric field that induces cDEP as described previously, and secondly superposing the rotating electric field [59].

For the trapping step, the four electrodes are powered with opposite phase sine waves (angular frequency $\omega_{1}$, amplitude $\hat{V}$, see Fig. 6.15). The resulting force field pushes the cell towards the center of the electrode set due to nDEP.

Fig. 6.15

Single cell trapped by negative dielectrophoresis (red arrows) at the center of a four electrode set, being powered by alternate polarities of sinusoidal voltages. The cell experiences a levitation force (blue arrow) at the center of the electrode set, due to higher order of the force

The cell also experiences a levitation force, that cannot be described by the Eq. 6.105 as the electric field is null for any altitude along the line at the center of the electrode set. Indeed Eq. 6.105 remains true as long as the electric field is homogenous all over the volume of the handled dielectric particle, that can be considered in that case as a dipole. In the case where the cell is centered by the four-electrode set, it experiences higher moments of the force [83, 84] and it is finally pushed not only where the electric field is minimal but also where its gradient is minimal (if the second order is considered). The second order approximation of the dielectrophoretic force along the z-axis can be expressed as a function of the first order and second order potential energies $U_{1}$ and $U_{2}$:

$$ F_{depz} = - \frac{\partial }{\partial z}\left( {U_{1} + U_{2} } \right) $$

(6.111)

where

$$ \begin{aligned} U_{1} & = 2\pi \varepsilon_{m} R_{cell}^{3} f_{CM} E^{2} \;{\text{and}} \\ U_{2} & = \frac{2}{3}\pi \varepsilon_{m} R_{cell}^{5} f_{CM2} \left( {\left( {\frac{{\partial^{2}\Phi _{e} }}{{\partial x^{2} }}} \right)^{2} + \left( {\frac{{\partial^{2}\Phi _{e} }}{{\partial y^{2} }}} \right)^{2} + \left( {\frac{{\partial^{2}\Phi _{e} }}{{\partial z^{2} }}} \right)^{2} } \right) \\ & \quad + \,\frac{4}{3}\pi \varepsilon_{m} R_{cell}^{5} f_{CM2} \left( {\left( {\frac{{\partial^{2}\Phi _{e} }}{\partial y\partial z}} \right)^{2} + \left( {\frac{{\partial^{2}\Phi _{e} }}{\partial z\partial x}} \right)^{2} + \left( {\frac{{\partial^{2}\Phi _{e} }}{\partial x\partial y}} \right)^{2} } \right) \\ \end{aligned} $$

(6.112)

$\Phi _{e}$ being the applied external potential $\vec{E} = - \vec{\nabla }\Phi _{e}$ and $f_{CM2}$ the second order generalized Clausius-Mossotti factor:

$$ f_{CM2} = \frac{{\varepsilon_{cell}^{*} - \varepsilon_{m}^{*} }}{{2\varepsilon_{cell}^{*} + 3\varepsilon_{m}^{*} }} $$

(6.113)

The cell stabilizes at an altitude where the levitation force is balanced with the gravitational force [85].

The z positioning of the cell above the plan of the device surface is better controlled using octopolar electrodes [86]. In that case, the two superposed quadrupolar set of electrodes repulse the cell along the z axis, the equilibrium position being slightly below midway between the two planes, due to the gravitational force. Such a 3D device structure is more complicated to fabricate than the simple coplanar device, but ensures an easier control of the cell altitude, getting rid of any friction between the cell and the device ceiling or floor (see Fig. 6.16).

Fig. 6.16

From [86], reproduced with the permission of Royal Society of Chemistry

Single cell captured, levitated and submitted to electrorotation experiment with an octupolar electrode set. The cell is centered and levitated midway between the two layers of electrodes, thanks to the application of a stationary field (voltage amplitude A and angular frequency $\omega_{1}$) to which the rotational field is superposed (voltage amplitude B and angular frequency $\omega_{2}$, 90° phase shift).

6.3.3.3 Some Application Examples of Electrorotation Experiments

The dielectric parameters of various biological components, including either single cells or cell assemblies could be determined using electrorotation experiments. For example, the viability of unicellular protozoan pathogens was assessed using that method, for the disinfection of water [87]. For more fundamental purposes, the dielectric properties (conductivity and permittivity) of the different components (outer wall, cytoplasm) of procaryotic cells were investigated in [88]. The dielectric parameters of eucaryotic cells were monitored using the same method, to determine the evolution of the conductance and permittivity of their cytoplasmic membrane and inner compartment, once submitted to permeabilizing pulsed electric field [82]. The same protocole was used to investigate the structural changes in spheroids in [89].

The biocomponent dielectric parameters were estimated by minimizing the distance between the measured spectrum of the rotational velocity of the cell $\Omega _{cell} \left( \omega \right)$ and the theoretical one, using least square criteria. The dielectric properties (σ and $\varepsilon$ of the outer membrane, periplasmic space, inner membrane, and cytoplasmic compartment) of bacteria were assessed by this method using a spectrum range for $\omega$ up to 1 GHz, on the basis of a three-shell model [88]. In the same way, the dielectric properties of the external wall and inner space of ellipsoid shaped yeasts were determined in [90] as well as the dielectric behaviour of various shape algae [91].

6.3.4 Dielectrophoresis of Biomolecules

Biological applications of DEP are not limited to cells and DEP has also proved to be useful for the concentration, separation and detection of biological entities as small as proteins, DNA and viruses. However, while the DEP behavior of cells is well understood, the polarization mechanism of biomolecules is not fully elucidated. In the case of DNA, the underlying mechanism inducing DEP motion is mainly attributed to counterion response to AC electric fields. Negatively charged phosphate groups along the DNA backbone attract positive counterions from the surrounding ionic solution, which migrate in response to the applied field (Fig. 6.17).

Fig. 6.17

From [89], reproduced with the permission of Springer

Capture and electrorotation experiment of biocomponents for the estimation of their dielectric parameters. Left figure: B16F10 cell (murine melanoma cell) motioned by a set of four polynomial electrodes (inter-electrode distance 70 µm). Right figure: a spheroid (U87MG cell line) is positioned in a larger set of electrodes (inter-electrode distance 150 µm) for electrorotation experiment.

The resulting shift in the counterion cloud results in an induced dipole moment which is assumed to be responsible for DNA DEP behavior [92]. Washizu and coworkers pioneered the concept of DNA DEP more than twenty years ago by demonstrating the stretching of DNA molecules under a field strength of 10⁶ V/m and a frequency of 1 MHz. The size (number of base pairs) of the stretched DNA molecule could thereby be determined and target DNA fragments could be cut using a UV beam [93]. This group also demonstrated that synthesized oligonucleotides having 22 bases could be separated from λ-DNA (having 48.5 kbp) using DEP-FFF. The larger molecules showed higher polarisation and were retained onto the electrodes placed at the bottom of the separation chamber, while the smaller oligonucleotides could flow more easily through the channel [94]. Tuukkanen et al. also demonstrated trapping of DNA molecules as small as 27 base pairs, which shows that DNA manipulation can be achieved over a broad range of sizes [95]. It should be noted that real-time observation of DNA motion is typically achieved using fluorescence microscopy and therefore requires DNA staining.

DEP is also an interesting tool for protein concentration, which is often a prerequisite in bioanalytical applications, since proteins, unlike DNA, cannot be amplified. Most proteins are around 1–10 nm in size. Given the fast decay of $F_{DEP}$ with the cube of the particle radius and the influence of Brownian motion on small objects, large electric field gradients are therefore required to enable their manipulation ($\nabla E^{2}$ as high as 10¹⁵–10¹⁶ V²∙ m⁻³). The different devices reported for protein DEP were recently reviewed by Nakano and Ros [96]. Clarke et al. increased the concentration of immunoglobulin G proteins by a factor of 300 at the tip of a capillary glass of inner diameter 100–150 nm using electrodeless dielectrophoresis. An electric field of $10^{6}\,{\text{V}} \cdot {\text{m}}^{ - 1}$ was generated in the tip of the nanopipette on application of a 1 voltage between the electrodes in the pipette (ground electrode) and bath solution (working electrode). The tip acts as a constriction used to create a high-field gradient with a local maximum, allowing protein trapping by pDEP [97]. While this study was aimed at concentrating proteins in the bulk, it is also possible to immobilize proteins on surface using DEP without the need for any chemical modification. Otto et al. have achieved dielectrophoretic immobilisation of antibodies on a regular array of cylindrical sub-microelectrodes and could demonstrate that the antibodies capability to bind to target proteins was preserved after DEP application [98].

6.3.5 Conclusion

In this section, we have presented the basic principles of three AC electokinetic phenomena, namely dielectrophoresis, twDEP and electrorotation. A summary Fig. 6.18 schematically depicts some device geometries discussed above. While the given examples were mainly focused on cell handling applications, there are many other applications of DEP to nano biosystems, such as controlled assembly of carbon nanotubes for the development of biosensors [100] or specific capture of proteins using beads coated with antibodies [101], for instance. Dielectrophoresis can also be combined with other force fields such as acoustophoresis or magnetophoresis, so as to develop hybrid systems allowing multitarget and multicriteria cell separation [102]. It should also be noted that depending on the operating conditions (frequency and intensity of the electric field), other electric field-induced forces may arise during a DEP experiment, which requires a proper understanding of other AC electrokinetic phenomena involving liquid actuation such as AC electroosmosis and electrothermal effects (see Sect. 6.2). While these phenomena may induce perturbations in some cases, they can also be exploited in conjonction with DEP to provide a large panel of manipulation approaches [103, 104].

Fig. 6.18

Bioparticles trapped by nDEP and pDEP are represented in blue and red, respectively. 2D planar electrodes: a Quadrupolar electrodes of polynomial design. b Interdigitated array (IDA) of rectangular electrodes. c Parallel electrodes than can also be arranged as a large IDA as in [99]. d 3D electrodes: e Top bottom electrodes (adapted from [62]). f Sidewall electrodes [63]. IDEP electrodes: g Circular insulating post array used to repel proteins from the constrictions where the electric field is maximum [65]. h Nanopipette used to trap proteins using pDEP [97]. tw-DEP electrodes: i Spiral electrodes used to separate cells using a propagative electric field [80]

6.4 RF and Microwaves for Fluidics and Biodevices (Thi Hong Nhung Dinh, Stephane Serfaty, Pierre-Yves Joubert)

6.4.1 Introduction

Due to their structure and composition, organic materials have free and bound electrically charged entities. When excited by an external electromagnetic field, drifts and displacements of those charges are provoked, inducing conduction and polarization currents within the material. The dielectric properties of the material are a measure of these induced microscopic conduction and polarization phenomena, which constitute the response of the material to an external electromagnetic field.

Since the dielectric properties are determined by and informative about the nature, the composition and the state of the organic material, they are considered as valuable characterization parameters in many scientific and engineering fields involving organic material, such as agriculture, food industry [105,106,107] and healthcare [108]. In agrifood engineering, the dielectric properties are used e.g. to monitor the quality of food products [107, 109, 110], or to evaluate their state of integrity during maturation [111] or storage [112, 113]. They are also used to predict and control the effects of electro-thermal treatments such as sterilization or pasteurization on food products [105, 114, 115]. In the healthcare domain, the dielectric properties provide relevant information about the physiological state of biological cells and tissues. They are a way of monitoring the state and changes occurring in biological material, which can for example lead to the elaboration of medical diagnosis of tissue pathologies such as inflammation, burns, tumors, etc. [116,117,118,119,120,121,122]. Indeed, natural evolutions of organic material such as maturation or ageing, material modifications due to processing such as heating, freezing, or thawing…, or cell functional and/or morphological alterations appearing e.g. with pathologies, result in either structural alterations or changes in the complex biochemical content of the material. In all cases, these alterations induce significant modifications of the dielectric properties of the material. For example, cell membranes altered by electroporation feature modified dielectric properties, which can be read out through the measurement of the changes of the global cell bio-impedance in a 20 MHz frequency range [123]; in the same way, the dielectric properties of tissues with tumors are reported as exhibiting more than 70% changes relatively to those of sound tissues at around 100 MHz [124].

As a result, the dielectric properties constitute relevant indicators either for the monitoring of organic material changes, or for the detection, the characterization and the monitoring of pathologies. Due to the complex structure of organic material which includes macromolecules of various sizes and shapes, the dielectric properties are strongly frequency dependant. For these reasons, a wide range of dielectric characterization methods have been developed, involving electromagnetic fields operating especially in the radiofrequency (RF) and microwave (MW) bandwidths, i.e. including frequencies ranging from a few kHz to tens of GHz. This chapter aims at presenting the basics of the interactions taking place between electromagnetic fields and organic material, and at presenting typical dielectric sensing and characterization devices developed for various scales of organic material investigations. The chapter is organized as follows. Firstly, basics on the dielectric properties of organic material will be recalled, with emphasis on biomaterial such as cells and tissues. Secondly, examples of dielectric characterization methods and devices used for healthcare applications and operating from cell up to tissue scales will be presented.

6.4.2 Basics on the Dielectric Properties of Organic Material

6.4.2.1 Overview of Organic Material Structure and Composition

Biomaterials are highly heterogeneous materials which can be considered at various dimension scales, at described in Fig. 6.19. They are constituted of complex liquids including organic and mineral elements, macromolecules, water-insoluble matter such as fibers or tendons. The organization of these constitutive elements allows intra and extra cellular structures to be formed. At meso or macroscopic scales these structures appear to be homogeneous, and feature highly variable structural properties which, on a mechanical standpoint, range from liquid to solid state materials [125].

Fig. 6.19

Schematic representation of the dimensions scales in the human body

At a tissue scale, these structures can be considered as mainly immerged in an aqueous liquid. The resulting complex fluids include organic electrolytes and bio-molecules which interact with one another, and feature properties close to those of aqueous solutions, due to their molecular asymmetry, their electrically polarized nature and their hydrogen and molecular bonding. The particular arrangement and biochemical composition of each tissue provide specific functionalities, the biological and physical roles of which are fundamental within the whole biological system. Biological tissues may fall into two main families: (i) the connective tissues, which are constituted of entangled cells included in a kind of matrix featuring various stiffness properties, ranging from fluid like material (e.g. blood), to gel like material (e.g. adipose tissue) and solid state materials (e.g. bones); and (ii) the epithelial tissues featuring joined cells, such as skin.

At a microscopic scale, cells strongly contribute to the macroscopic evolution of the biological system. To do so, they possess specific functionalities, such as autoreplication, environmental protection, acquisition of nutritive elements, communication, degradation and renewing of intrinsic molecules, production of energy, etc. Despite their small size (1–100 µm), cells generally contains numerous components and feature structural properties of complex fluids [126].

The inner part of the cell includes a nucleus, a cytoskeleton made of a network of microtubules, some intermediary filaments, organelles of different size and shapes, proteins, all immerged in an intracellular solution (cytosol). The cell is covered by a phospholipid double layer membrane reinforced by proteins molecules. These proteins are formed with specific three dimensional structured polymers including hydrophobic sites, which depend on the affinity of hydrophilic polar groups present in the solution surrounding the cell. They are accompanied by large mounds of organic material. In aqueous solutions, these macromolecules behave like electrically polarized molecules featuring permanent or induced bipolar electrical moments of various magnitudes, depending on the size and shape of the molecules. Carbohydrates are also present at the surface of membranes, which are involved in cell communications, and also responsible for the secretion of lubricating gels in some tissues such as cartilage, tendons or ligaments. In aqueous solutions they modify the dispersion of water according to their concentration.

Finally, a large amount of electrolytes such as sodium, calcium, magnesium and chlorides play important roles in cell functioning and biological interactions. Numerous vital processes depend on the equilibrium between inner and outer cell electrolytes concentrations. The cellular membrane are globally impermeable to passive ions exchanges, but allow physiologically controlled unidirectional or bidirectional going through of ions. At that scale of operation, a loss of that subtle equilibrium e.g. due to a microbial infection may result in a chain reaction with possible severe consequences such as irreversible structural changes in the tissue. Such biological dysfunctions should be detected and characterized at an early stage so that an appropriate therapy can be proposed.

The involved nano/micro-scale biochemical content and structural changes result in the changes of the dielectric properties of the organic material, which may be observed at larger (micro to meso) scales of observations, providing appropriate dielectric sensing device can be developed.

6.4.2.2 Dielectric Properties of Biomaterial

Electrolytes, macromolecules, proteins, organic and mineral components which are present in cells and tissues are electrically active since they feature free electrical charges and bound electrical charge distributions, the displacement of which being induced by an electrical field applied. These effects are macroscopically described by the complex permittivity ε of the biological material (considered as homogeneous and generally isotropic) and which reads [127, 128]:

$$ \varepsilon = \varepsilon^{\prime } - j\,\varepsilon^{\prime \prime } = \varepsilon_{0} \varepsilon_{r} - j\frac{\sigma }{\omega } $$

(6.114)

In this complex expression, $j\,= \sqrt { - 1}$ and ω is the angular frequency. The real part εʹ = ε₀ε_r accounts for the permittivity of the material (where ε₀ is the permittivity of vacuum and ε_r is the dielectric constant of the material, also designated as the relative permittivity). The permittivity measures the induced polarization of the material by units of electrical field, i.e. the extent to which the bound charge distributions can be distorted and polarized under the influence of the field, and the consequent energy stored within the material. For organic material, these charge distributions are mainly associated with double layer membrane proteins, with the surface of solvated macromolecules or with other polar molecules [129].

The imaginary part $\varepsilon^{\prime \prime }$ of the complex permittivity $\varepsilon$ is relative to the dielectric losses associated with the displacement and conduction currents induced within the material by the applied field. In biological material, conduction currents are mainly due to the ionic free charges moving through the tissue under the influence of the field. These losses are proportional to the effective conductivity σ (Eq. 6.115) the material, expressed in S/m.

Each electrically active entity within the material structure will exhibit its own characteristic response to the applied field, according to its own nature, shape and size. As a result, the macroscopic terms $\varepsilon^{\prime }$ and $\varepsilon^{\prime \prime }$ (or ε_r and σ) exhibit a frequency dependant behavior. Besides, the proportion of the dielectric losses to the stored energy is given by the loss tangent so that:

$$ \tan \delta = \frac{{\varepsilon^{\prime \prime } }}{{\varepsilon^{\prime } }} = \frac{\sigma }{{\varepsilon_{0} \varepsilon_{r} \omega }} $$

(6.115)

In order to sense structural modifications of biological material through their macroscopic dielectric properties changes, it is relevant to chose the frequency of investigation at which the changes of $\varepsilon^{\prime }$ and $\varepsilon^{\prime \prime }$ are both significant, i.e. in the same order of magnitude. This condition is reached for:

$$ \tan \delta = 1 $$

(6.116)

As a result, for a given material, the ideal sensing angular frequency $\omega_{n}$ would be so that:

$$ \upomega_{n} = \sigma /\varepsilon_{0} \varepsilon_{r} $$

(6.117)

Around this characteristic angular frequency $\omega_{n}$, the frequency response of the material to an electrical stimulus features a Debye-type form [130] which, in terms of relative permittivity, reads:

$$ \upvarepsilon_{r} =\upvarepsilon_{r\infty } + \frac{{\upvarepsilon_{{r{\text{s}}}} -\upvarepsilon_{r\infty } }}{{1 + j\frac{\upomega}{{\upomega_{n} }}}} $$

(6.118)

where $\omega_{n}$ is the characteristic angular frequency relative to the so-called relaxation time$\tau = 1/\omega_{n}$, $\upvarepsilon_{r\infty }$ is the relative permittivity at an angular frequency sufficiently high compared to $\omega_{n}$ and $\varepsilon_{rs}$ is the static relative permittivity. A similar form can be written for the conductivity.

6.4.2.3 Relaxation Times Relevant for the Sensing and Characterization of Organic Material

Because of the complexity of the organic material structure, dielectric properties changes due to material alterations may occur at various scales. The difficulty for developing devices able to sense these alterations lies in the choice of the most relevant investigation frequency, since several relaxation times may be distinguished for biological tissues. Indeed, due to multiple interactions occurring at multiple scales, four relaxation times are experimentally observed in the 1 Hz–100 GHz [130,131,132,133]. They are modeled by means of the Cole-Cole-Davidson weighed complex sum form [131, 132, 134]:

$$ \upvarepsilon = \varepsilon_{\infty } - j\frac{{\sigma_{s} }}{\omega } + \mathop \sum \limits_{n} \frac{{\Delta \varepsilon_{n} }}{{1 + \left( {j\frac{\omega }{{\omega_{n} }}} \right)^{{1 - \alpha_{n} }} }} $$

(6.119)

where Δε_n is the permittivity change ($\Delta \varepsilon_{n} = \varepsilon_{n} - \varepsilon_{\infty }$), ε_n is the static permittivity for relaxation n, α_n is the a frequency dispersion coefficient relative to relaxation n. This model can be adjusted to fit with experimental data and is generally limited to a 3-pole simplified model in a 3 decade frequency bandwidth [30, 32, 33]. It may also be relevant to consider the imaginary and real parts dependancy so that the permittivity frequency response writes [135, 136]:

$$ \upvarepsilon = \varepsilon_{\infty } - j\frac{{\sigma_{s} }}{\omega } + \frac{{\Delta\upvarepsilon}}{{\left( {\left( {j\frac{\omega }{{\omega_{n} }}} \right)^{\alpha } + \left( {j\frac{\omega }{{\omega_{n} }}} \right)^{1 - \beta } } \right)^{\gamma } }} $$

(6.120)

where α, β, γ are real coefficients taking values in the [0, 1] range. The adjustment of these coefficients allows models rather close to observed dispersion data to be elaborated in a large frequency bandwidth.

In order to sense material structural alterations, it is necessary to determine the relevant frequency range. Published experimental studies on biological tissues point out that a main relaxation time arises around a few tens of MHz for typical tissues, depending on the actual aqueous content of the tissue [137, 138] (Fig. 6.20).

Fig. 6.20

Frequency dependence of the dielectric parameters of typical high water content biological tissues [140]

High water content biological tissue exhibit three main dispersion areas commonly called α, β and γ dispersions, as depicted in Fig. 6.20. In the low frequencies (below 10 kHz), the α-dispersion is characterized by a rather large dispersion on the relative permittivity, which may be partly attributed to the diffusion of electrolytes. Other complexes mechanisms have also been reported in the literature [139]. Several interactions occurring next to the cell membrane surfaces are also involved, such as hydrophilic—hydrophobic interactions in the protein double layer membrane, ionic canals, etc. Due to the size and shape of the involved macromolecules structures, several dispersions might be superimposed. The ionic equilibrium between extra and intra cellular media which are separated from around 6 nm, can also significantly modify the dispersion in that area.

The β-dispersion, is considered as extending along a 4 decade frequency bandwidth typically centered around 10 MHz (Fig. 6.20). It is due for one part to the polarization of various macromolecules within the intra cellular media, but mainly to the interfacial polarization of the cell membranes. The latter acts as a barrier for passive ion transport, the efficiency of which depending on the frequency of the applied electrical field. These interfacial polarization phenomena have been theoretically and experimentally studied [141]. Some simplified models build with double layered spherical systems included in ionic liquids foresee the presence of a number of dispersion directly related to the number of interfaces [142, 143]. Besides, it was experimentally established that damaged cell membranes modify the β-dispersion. Hence, numerous biomedical applications are based on the monitoring of the β-dispersion which is related to physio-pathological state changes of biological material, induced by cell morphology or cell physiology modifications. Finally, the γ dispersion is related to the polarization of water molecules and therefore occurs in a higher frequency range (>1 GHz). The detection of pathologies involving water content modifications such as enhanced vascularization due to the presence of tumors can be detected through the monitoring of the γ-dispersion of the dielectric properties of tissues.

6.4.3 Dielectric Characterization Techniques

Pathological alterations implying micro-scale or nanoscale structural modifications of cells inner material and cell interfaces should be detectable through the monitoring of the complex dielectric properties of tissues at a mesoscopic scale of investigation. To that respect, the use of electromagnetic waves corresponding to the β-dispersion, seems particularly relevant to monitor tissue changes (i) due to cell structural modifications in dense areas through the changes of the polarizability of the material, or (ii) to the modifications of dissolved ionic components in soft material through the modification of the conductivity. Higher frequencies of investigation should help to downsize the scale of investigation, so that higher order dispersions and refined cell model could be considered.

For that reason, numerous dielectric characterization techniques have been developed in a wide frequency bandwidth ranging from a few kHz up to tens of GHz. Most developed devices operate at a meso-scopic scale to carry out tissue level investigations. However, micro-scale dielectric sensing devices involving microfluidic environment are more and more developed so as to investigate down to the biological cell level, and constitute high accuracy label-free biosensors. In this section, the main dielectric characterizations techniques are recalled and some examples of organic material dielectric sensing applications involving meso-scale (tissue-level) or micro scale (cell-level) characterizations, are presented.

6.4.3.1 Electrical Impedance Spectroscopy

The electrical impedance spectroscopy (EIS) is a measurement technique allowing the bio-impedance of organic material to be sensed over a frequency bandwidth which, in practice, generally operates from a few kHz up to 100 MHz. The basic principle of the measurement is to inject a small frequency-adjustable alternating current within the material, and to measure the voltage drop appearing between two (or more) electrodes, which are either deposited on or inserted within the material.

The bio-impedance of the material is determined using ohm’s law, and gives information which is related to the local dielectric properties of the investigated material. This technique is widely used and is proven efficient in various medical applications such as tissue pathology diagnostic or monitoring, e.g. for cell [123], tumor [145] or wound healing [146] characterizations. In its simplest form, EIS can be implemented using a two-electrode scheme, as presented in Fig. 6.21a. Two electrodes are placed in contact with the material and connected to the impedance measurement device. The electrical equivalent circuit is presented in Fig. 6.21b, in which Z_bio is the bio-impedance to be measured, Z_i are interface impedances, Z_in is the measurement device input impedance, supposed to be “infinitely high”, so that:

Fig. 6.21

Bio-impedance measurement schemes for Electrical Impedance spectrosctopy; a. Two-electrode measurement scheme. b. Electrical equivalent circuit model of Two-electrode measurement scheme. c. Four-electrode measurement scheme—Electrical equivalent circuit model of four-electrode measurement scheme. Inspired by [144]

$$ \frac{v}{i} = 2Z_{i} + Z_{bio} $$

(6.121)

The injected current i being known, the voltage drop v being measured, it is possible to estimate Z_bio providing Z_i is small enough or previously determined using a calibration procedure. A highly demonstrative experiment aiming at illustrating the relevance of the EIS to characterize organic material was proposed in [147] as a experimental training for undergraduate students. The experiment is based on set up presented in Fig. 6.21a. It consists in inserting a pair of pin electrodes into a potato used as an easy to handle biomaterial, and in measuring the resulting bio-impedance at the end of the electrode pair in the 100 Hz–20 MHz bandwidth. In this frequency range, it is mostly the ionic conduction that affects the bio-impedance. Here, Z_i is considered as negligible and a v/i Bode plot enables Z_bio to be visualized over the whole frequency range. The observed electrical phenomenon can be modeled as depicted in Fig. 6.22: an elementary equivalent circuit is established which includes (i) a resistance R_ext, accounting for the electrical conductivity of the extracellular matter, (ii) a resistance R_in accounting for the intracellular conductivity and (iii) a capacitor C_ext modeling the cell membrane ion-barrier.

Fig. 6.22

Conductivity dispersion (a) and equivalent electrical circuit model (b) of the bio-impedance of an elementary organic material (potatoe), [147]. Typical values issued from the fit with experiment data are: R_ext ≈ 8 kΩ, R_in ≈ 300 Ω, C_ext ≈ 1 nF [147]

This model is quite coarse, however it gives a rather good image of the macroscopic electrical behavior of tissues, e.g. for human skin [148]. It can be refined introducing a so-called constant phase element which is a fractional power capacitor modeling the discrepancies between cells within the tissue [149]. The resulting bio-impedance electrical model then reads:

$$ Z_{bio} = R_{\infty } + \frac{{R_{\infty } - R_{0} }}{{1 + (j\omega \tau )^{\alpha } }} $$

(6.122)

where R₋ is the high frequency resistance, R₀ is the static resistance, is the relaxation time, and α is a parameter taking values in the [0 1] interval.

Here, the electrical circuit model of Fig. 6.22b. provides an acceptable model that fits with the measured potato EIS data. In the low frequencies (f < 10 kHz), Z_bio= R_ext since ionic current lines are limited to the extracellular matter (C_ext acts as an open circuit). For high frequencies (f > 10 MHz) Z_bio = R_ext // R_in since ionic current flows through both the extra and intra cellular matter (C_ext acts as a short circuit). In this frequency range, the resistance of the material is reduced (R_in ≪ R_ext) which corresponds to an increased conductivity. For midrange frequencies (around 200 kHz), a transient electrical behaviour is observed. It corresponds to a β-type dispersion in which the cell membrane barrier progressively opens to the ion flow, and in which consequently the conductivity increases (as presented in Fig. 6.20. In order to put into light the change of the material electrical properties with the alteration of the biomaterial, Français et al. propose to provoke an electroporation of the cell membrane [147] and to measure the resulting bio-impedance changes. The electroporation consists in applying electrical field pulse sequence to the organic material (e.g. a sequence of 10 rectangular pulses of 100 µs duration separated from 1 s, and featuring a 500 V/cm intensity between the electrodes), so as to actively induce the formation of pores within the cell membranes. After electroporation, the measured EIS data are significantly changed and may be modeled by new electrical element values. In particular, the R_ext value is reduced by a 20–30% rate, resulting from the increase of the ionic conductivity of the material resulting from the provoked poration of the cell membranes. Based on the approach, the EIS difference between electropored and untreated tissues (lung, heart, …) of small animals was successfully highlighted in a 10 MHz bandwidth, showing 50–80% magnitude changes at 200 kHz [150]. Also, normal and malignant mice breast tissues were successfully diagnosed using EIS in a 100 Hz–1 MHz bandwidth [151].

The two-electrode measurement scheme might be found inaccurate when the interface impedances Z_i cannot be ignored or previously measured. To that end, a four-electrode scheme depicted in Fig. 6.21b. can be preferred. In this scheme, the bio-impedance Z_bio is directly given by the ratio v/i, whatever the values of Z_i, providing the measurement device feature an high input impedance Z_in and providing appropriate placement of the four electrode set (Fig. 6.22). Lukaski et al. evaluated the efficiency of the four-electrode bio-impedance measurement to non-invasively and reliably monitor the healing of cutaneous wounds [146]. Surface electrodes were placed at each side of a wound (19 mm in length, 17 mm in width, and 2 mm in depth) as depicted in (Fig. 6.23) and the monitoring of the real part (R), the imaginary part (X_c) and the phase angle (PA) of the bio-impedance was carried out over the healing period (tens of days) at a 50 kHz frequency. In this work, the real part R was found to be inversely proportional to the amount of extracellular fluid and directly proportional to the fibrin clot and epithelialization, thus correlated to the successful wound healing. Similarly, X_c was found to be proportional to the cell mass, through the polarizability of the cell membrane. As a result, increases in X_c indicate epidermal proliferation whereas X_c decreases with infection and cell loss. Healthy membranes cause a delay in the transit of voltage and current; thus, the greater the PA, the healthier the cell membranes, and decreases in PA reflect impaired membrane function. For uncomplicated wound healing, the observed general pattern is a continuous increase in R, X_c, and PA that is consistent with decreased extracellular fluid, increased cell mass, vitality and epithelialization.

Fig. 6.23

Four-electrode EIS of a cutaneous wound, inspired by [146]

The EIS approach can be extended to electrodes arrays, in order to provide spatially resolved bio-impedance characterizations. To this end, a two dimensional (2D) bio-impedance measurement device was proposed in [145] to locate and characterize pathological epithelial tissues in a 0.1 Hz–100 kHz bandwidth. The device uses 64 units of four electrode sets (256 electrodes), providing a 2D bio-impedance image of the investigated tissue with a 400 µm × 400 µm resolution. The device was successfully implemented on a pig tissues (skin, tong) to detect and characterize wound extends. Based on this approach, 2D or even 3D EIS imaging techniques were developed for breast tumor detection [119]. Even if contact issues, resolution issues, and electrode distribution issues were observed, preliminary clinical examinations showed promising results fully or partially consistent with X-ray mammography and biopsy [152]. More recently, a flexible micro-electrode array has been proposed in [153] for the early detection of pressure ulcers in vivo. The array is fabricated by means of an inkjet printed technology and features a hexagonal configuration of 55 equally spaced (≈2 mm apart) gold electrodes printed on a 35 µm polyethylene naphthalate flexible substrate, and electrically connected to the tissue via highly conductive hydrogel bumps printed above the electrodes. The array is placed on a wound in vivo and the electrical impedance is collected in a 100 Hz–1 MHz bandwidth for each pair of neighboring electrodes. Maps of impedance magnitude, phase angle and post-processed damage threshold are constructed based on the location of each electrode measurement pair. The array enables the non-invasive assessment of pressure induced tissue damage on a rat model, with sufficient sensitivity and robustness to carry out the early detection of mild and reversible wounds that are not visually observable. Even if actual clinical test have to be performed, this device arise promising applications to prevent irreversible tissue damage. The examples presented above illustrate macroscopic implementations of EIS, which give macroscopic electrical information related to microscopic phenomenon. A reduced scale of investigation may be obtained using lab on chips in a microfluidic environment, where cell EIS might be carried out.

For example, Fernandez et al. [154] proposed a flexible label free sensor aiming at assessing the viability and biomass of cells, through the measurement of their bio-impedance. To do so, yeast cells are grown, collected and suspended in a dionized water solution. The cell suspension flows within microfluidic channels equipped with parallel electrodes placed at each side of the channel. The electrical impedance viewed from the electrodes is modeled with an electrical circuit constituted of electrode stray resistances and capacitances, of the resistance of the extracellular solution flowing in the channel, of the intracellular cytoplasmic resistance R_cyt and of the cell membrane capacitance (C_m). In order to solely sense R_cyt and C_m that are related to the cell dielectric properties, a differential microfluidic device featuring two channels equipped with electrode pairs separated by different distances is build up. The differential structure of the device enables to determine the permittivity of the cell from the evaluation of R_cyt and C_m, using a Cole-Cole model of the cell permittivity in a 0.3–50 MHz bandwidth. Experimental results show that viable cells exhibit an electric impedance spectrum which is different in amplitude and in relaxation time from heat treated cells, which are altered in their shape and electrical parameters (R_cyt and C_m) due to membrane degradation. In the same way, Bürgel et al. [123] proposed an on-chip single cell microfluidic integrated device allowing for the electroporation and the EIS of single cells in suspension (Fig. 6.24). Paired electrodes are used to induce the cell electroporation and to carry out the EIS analysis. Here, the electroporation is achieved by exposing the cell to an electric field of 2 kV/cm at 50 kHz in a single passage. The passage of single cells is detected and impedance measurements are performed at 8 frequencies distributed in the 20 kHz–20 MHz range, constituting the EIS. After baseline removal (subtraction of the EIS of cell-free solutions) and electrical modeling of the channel/cell impedances, the effect and dynamics of the electroporation of HeLa cells were clearly demonstrated through on-chip EIS analysis.

Fig. 6.24

Single cell EIS and electroporation microfluidic device. Schematic presentation, as described in [123]

For practical reasons, EIS techniques are generally limited to a 100 MHz bandwidth above which the simple electrical equivalent R-C modeling of the sensing system no longer applies [155]. However higher investigation frequencies may be necessary to reach more thorough characterizations involving higher frequency dispersions or reduced investigation scales, so that refined material models such as layered tissues, multi-shell cell models, etc. can be elaborated. To do so, waveguide based dielectric sensing devices must be considered.

6.4.3.2 Waveguide Based Dielectric Sensing

Designing high frequency sensing devices requires the use of waveguide based sensors. Indeed, high frequency excitation signals generate electromagnetic wavelengths that might reduce down to the same dimensional sizes as the device, so that quasi static assumptions no longer apply. The design of waveguides based sensing devices enables electromagnetic wave propagations to be controlled, so that appropriate sensor model might be developed. Numerous waveguides based techniques have been developed for dielectric characterizations since the 1940s [156]. They fall into two main categories: the transmission measurement techniques, and the reflectometric measurement techniques.

In transmission measurement methods, a two-port waveguide is implemented (Fig. 6.25). The incident wave is injected in port-1 and transmitted to port-2. The organic sample is inserted in or placed next to the waveguide, so that the transmitted electromagnetic wave is altered by the dielectric properties of the sample. A vector network analyzer (VNA) is used to determine the complex transmission coefficient S₂₁ defined by the ratio between the transmitted wave (measured in the port-1 reference plane) and the incident wave (measured in the port-2 reference plane). In the same way, the reflectometric measurement method uses a waveguide device including or placed next to the sample under test (Fig. 6.25). The characterization of the sample consists in determining the complex reflection coefficient S₁₁ defined as the ratio between the reflected and injected waves in the port-1 reference plane, by means of a VNA. Reflectrometric methods based on the use of coaxial probes are the most popular techniques and have been widely used for the dielectric characterization of organic material, thanks to their easy and non-invasive implementation features. Coaxial probes are generally made of a open-ended coaxial transmission line, possibly terminated by a dielectric bead, and set directly in contact with the considered material, enabling ex vivo as well as in vivo characterizations. The accuracy of the method requires (i) a good contact between the probe and the material, which is generally reached with organic materials in the form of liquids, gels or malleable solids, and (ii) some calibration process using reference liquids [156] such as di-ionized water, ethanol, and methanol solutions [157].

Fig. 6.25

Transmission and reflectrometric waveguide based measurement methods

Gabriel et al. [158] elaborated a database of the dielectric properties of a wide range of excised animal tissue in a 20−37 °C temperature range, and over a 20 GHz bandwidth by means of coaxial probes, and a four dispersion Cole-Cole model associated to a static ionic conductivity term (Eq. 6.6) have been used to reduce the complexity of various human and animal tissues (brain, fat, breast, skin, bone, liver, etc.) [138]. A 3 mm diameter precision open-ended coaxial probe was used in [120] to assess the in vivo complex permittivity of normal and malignant human liver tissues, converting the measured reflexion coefficient into the tissue complex permittivity using the de-embedding and rational function models described in [157]. In the context of the enhancement of controlled electrical intra-cardiac chirurgical operations, Brusson et al. [118] used a precision coaxial probe in the 0.8–2.6 GHz range to correlate the depth of electrically induced heart tissue burns (and quantified by microscopic observations) with the measured complex reflection of the implemented probe, in the 0–6 mm depth range. Caduff et al. proposed a waveguide based multisensory approach to carry out non invasive glucose monitoring [159]. Indeed, it has been established that blood glucose variations induce changes in the skin and underlying tissues (SAUT) dielectric properties. In order to sense these changes, a set dielectric sensors were designed to investigate the SAUT in the 1–200 kHz low frequency range, the 0.1–100 MHz middle frequency range and a 1–2 GHz microwave range. The kHz range sensors feature interdigited EIS-like electrodes, the MHz range sensors are constituted of 3 reflectometric capacitive sensors of various sizes, and the GHz range sensors are constituted of 2 coplanar waveguide transmission lines. The sensors were designed so as to investigate the SAUT at various skin depths, allowing glucose induced dielectric changes to be sensed within the underlying tissues, or non-glucose related changes e.g. due to skin-sweat or temperature changes, to be sensed in the upper skin layers. All dielectric sensors are integrated within the same sensory plateform, set on a bandage like device placed around the arm, together with conventional sweat, temperature and optical diffuse reflectance sensors. Statistical clinical studies highlighted the correlation of the developed non invasive multisensory data-fused glucose monitoring approach, with observed blood glucose concentrations [159].

As illustrated above, reflectometric dielectric sensors are relevant for non-invasive ex vivo or in vivo implementations on tissues. For practical reasons transmission methods are less suitable for this kind of characterizations since the considered sample should be inserted into the waveguide [156]. However waveguide transmission sensing techniques find wide applications in microfluidic characterization devices, where micro-device designs allow micro-strip transmission lines to be judiciously combined with microfluidic channels. For example, Leroy et al. [160] proposed a microfuidic biosensor designed for the dielectric spectroscopy of micro-scale particules flowing in a microchannel. The sensor is based on a discontinuated coplanar microstrip transmission line, constituted of 15 µm thick gold electroplated electrodes deposited on a fused silicate substrate. The microstrip line discontinuity is designed to form a capacitive sensor in a detection micro-area, above which a SU8 microchannel are patterned and covered with a PDMS top (Fig. 6.26a). Dielectric measurements are performed on 12 µm diameter polystyrene beads up to 8 GHz, through the measurement of the transmission coefficient S₂₁ of the transmission line carried out by a VNA. Measurements clearly demonstrate the ability of the device to sense the presence of single particule suspended in a di-ionized water solution, with a 1fF capacitance contrast. Similar experiments conducted with a 5 GHz resonant implementation allows 10 MHz resonance shift to be observed with single beads, from which adequate post processing computations enable the permittivity of the bead to be estimated. Finally, trials carried out on cancerous colorectal cells showed promising results, although dispersions in the size of the cells make the post processed estimation of the cell permittivity less accurate than that obtained with calibrated beads. Grenier et al. proposed a biosensor based on the use of a coplanar transmission line with a fluidic channel integrated on the top surface (Fig. 6.26b) [161]. The device is implemented as a two-port transmission sensor operated in the 0.4–35 GHz, and used to quantify the concentration of human umbilical vein endothelial cells suspended in a sucrose and fetal bovine water-based solution. The complex permittivity of the biological solution was estimated from the measured S₂₁ parameter through a dedicated de-embedding technique and modeling of the measurements using numerical computations a Cole-Cole modeling. A 100% change in the relative permittivity was observed between the cell-free solution and the 100% cell concentration fluid at 20 GHz, validating the relevance of the developed device as a non invasive label-free biosensor allowing cell quantification and counting to be carried out.

Fig. 6.26

Transmission line based dielectric sensors. a. Sensing capacitance inserted in a transmission line in microfluidic channel, from [160], b. Schematic view of RF interaction between a coplanar waveguide and a biological solution, which is localized in a microfluidic channel, from [161], c. Inter-digitated comb capacitors (IDC) set in a microwave coplanar waveguide, from [162]

A last example is provided by the sensor developed in [162], which aim at distinguishing the inner content of cells in order to discriminate cancer cell according to their evolution stage, by means of waveguide transmission based microfluidic biosensors. The developed sensor is a resonating device constituted of a meandered inductor and two inter-digitated comb capacitors set in parallel and implemented in a microwave coplanar waveguide, integrated with a SU8 patterned chamber on the top (Fig. 6.26c). The device acts as a stop-band transmission line for which the S₂₁ coefficient shows a minimum value at the resonance frequency of the formed LC resonator. Cells are deposited in the chamber using a droplet technique, and are trapped within the inter-digitated comb capacitor fingers (Fig. 6.26c). The presence of cells locally modifies the inter-digitated comb capacitor capacitance, and hence the resonance frequency of the whole resonator. For example, the presence of two cells in the chamber induces a shift of the S₂₁ resonance frequency of 89 MHz, for a 7 GHz cell-free sensor resonance. The study carried out on various cell lines allowed a clear correlation to be established between cell lines—especially between cells with low and high aggressiveness levels—and the electromagnetic signature constructed from measurements provided by the implemented biosensor and Cole-Cole modeling.

6.4.3.3 Contact Free Dielectric Sensing

EIS and waveguide based dielectric sensing methods use probes or sensors requiring an electrical contact with the organic material under test. These techniques are proved relevant however induce some possible contact issues including biocompatibility, loss of accuracy, loss of non-invasivity or comfort in the case of in vivo or wearable devices [156, 163]. For that reasons, free space or non-contact sensing techniques have been developed. In the low frequency spectrum (kHz up to tens of MHz), inductive methods generally referred as magnetic impedance techniques (MIT), use a non-contact magnetic coupling induced between an inductive antenna and the organic material to electrically characterize the material under test [119]. However, in practice, these techniques are mostly sensitive to conductivity changes occurring in the organic material, and are hardly sensitive to the dielectric constant [164, 165]. In the upper range of the RF and MW frequencies (1–100 GHz), free space techniques using MW antennas and RADAR imaging based approaches have been developed for non-contact and non-invasive dielectric characterizations especially for breast cancer detections [122, 166,167,168]. More recently, integrated systems operating in the 1–10 GHz band based on time domain multi-static RADAR techniques involving antenna arrays have been developed and previous clinical validations have been obtained for the efficient detection and localization of beast tumors [169, 170]. These systems allow advanced 2D dielectric image reconstructions to be achieved, and offer highly promising perspectives in terms of large scale development of low cost and easy to use breast cancer diagnosis devices.

Microwave bandwidth contact-free dielectric sensors often operate in the γ-dispersion area of tissues (Fig. 6.21), where the polarization of water molecules is mainly responsible for the dielectric behaviour of the tissue. Frequencies higher than the GHz are therefore relevant to investigate cancerous tissues since they feature increased vascularization compared to normal tissues. However GHz sensors are hardly sensitive to the conductivity of organic materials, although tumors and other tissue pathologies are known to features changes of both the real and imaginary part of the complex permittivity [116]. For that reasons, midrange RF frequency inductive techniques operating in the tens to hundreds of MHz bandwidth and related to the β-dispersion, have been developed for the non-contact assessment of the complex permittivity of organic materials.

For example, the technique developed in [171] is based on the use flat multi-turn split-conductor transmission-line resonator (MTLR) [172] distantly interacting as a transmit and receive inductive sensor with the considered organic material. The MTLR is monitored by a distant control coil fed with a low intensity RF current. When electromagnetically excited by the coil, the resonator generates an amplified RF magnetic field and induces the circulation of eddy currents and displacement currents within the organic material which depend on its dielectric properties. By reciprocity these currents modify the generated magnetic field, and hence, the impedance of the RF resonator. As a result, the measurement of the resonator impedance gives access to the dielectric properties of the investigated material. It is actually carried out through the evaluation of the impedance changes induced at the ends of the control coil (Z_mes) electromagnetically coupled to the resonator, by means of a VNA equipped with an impedance measurement kit. The whole set up is modeled by an equivalent electrical model as depicted in Fig. 6.27. [171]. In this electrical model, the R_c and L_c stand for the control coil, R₁, L₁, C₁ are the equivalent electrical lump elements of the MTLR, and R_i, L_i are the additional lumped elements induced by the conductivity and the permittivity of the material loading the MTLR, respectively [173]. Experimental feasibility of organic material non-contact characterization was realized for the in-line monitoring of milk fermentation during yogurt formation in [174]. To do so, milk solutions acidified with various concentrations of glucono-δ-lactone (GDL) were considered. The solutions were incubated at 37 °C so that micelles of casein aggregate under the combined action of the GDL and temperature, and so that the jellification process starts. Since the acidified milk solution features typical dielectric properties of σ ≈ 1.1 S/m and ε_r ≈ 65, the MTLR was designed so that the resonance frequency is around 300 MHz (according to Eq. 6.117). As a result, the used MTLR is a planar 19 mm large resonator constituted of two rolled-up 1 mm width transmission lines constituted of 35 μm-thick copper tracks deposited by photolithography on each side of a 250 μm-thick low-loss dielectric substrate (CuFlon). The designed MTLR features a practical resonance frequency f₀ = 306 MHz. The non-contact dielectric monitoring system was implemented during the jellification process of milk solutions featuring GDL concentrations of 13–26 g/l of GDL, and the dielectric parameters where extracted from the measurement of Z_mes using the electrical equivalent model (Fig. 6.27) and a calibration procedure implemented using a calibrated NaCl solution [175]. The resulting time evolution of both dielectric parameters is presented in Fig. 6.28. The observed conductivity and relative permittivity behaviour and kinetics are induced by the structural changes of the organic material during jellification, and are consistent with those observed with contact techniques [176]. Such non-contact approach offers interesting perspectives for the design of wearable sensors such bandage-like devices allowing the non-contact monitoring of wound healing or glucose content.

Fig. 6.27

Experiment set up and associated equivalent electrical modeling for non-contact dielectric characterization of organic material

Fig. 6.28

Evolution of the conductivity and relative permittivity versus incubation time for two milk samples acidified with different doses of glucono-δ-lactone (GDL)

6.4.4 Concluding Remarks

In this chapter, basics on the dielectric properties of organic material have been recalled and some examples of widely used dielectric characterization techniques have been presented. Finally, examples of dielectric sensing devices operating either at a tissue level or at cell–level of investigations have been presented.

These examples aimed at illustrating the relevance of dielectric characterizations to detect and monitor tissue pathologies in an accurate, non-invasive, non toxic and easily implemented manner. Thanks to the progress made in micro-fabrication processes as well as in sensing technology including data processing and communication, dielectric sensing devices are particularly good candidates be integrated in cheap and efficient point-of-care testing devices, as well as well as wearable sensing plateforms including microfluidic lab-on-chip biosensors or state-of-health physiological sensors.