Introduction

The relevance of external electric field (E-field) for healthcare in terms of nerve regeneration, bone fracture, and wound healing is well established [1, 2]. Depending on the applied stimulus parameters, a biological cell can be affected in a number of ways in the presence of the external stimulus [3,4,5,6,7]. Among various applications of external stimulation for healthcare, electric field-assisted cell growth [8], stem cell differentiation [9,10,11], and alignment [12, 13] as well as potential for selective electroporation of cancer cells [14, 15] have attracted wider attention [16, 17]. In fact, Panagopoulos et al. [18] suggested an E-field bioactivity diagram, where a particular combination of intensity (10 μW/cm2 at 20 cm distance), frequency (900–1800 MHz), and exposure duration (1–20 min) caused significant biological effects of electromagnetic fields in cell populations. Such effects can range from increased proliferation to even necrosis, depending on parameters like electric field intensity, frequency, and exposure time. For example, studies have shown that when low-intensity electric fields in a narrow range (1–5 V/cm) were used on L929 and osteoblast cell cultures on biomaterial substrates, an increase in cell proliferation was observed [16]. A large number of studies have shown that electric field can be a versatile tool in influencing cellular behavior and cell fate processes. This aspect of electric field stimulation of cell populations has been demonstrated in recent studies on stem cell differentiation into different lineages, such as osteoblasts, neuronal cells, muscle cells, and cardiomyocytes in conjunction with biomaterial substrates with potential applications in strategies for regenerative engineering [19,20,21,22,23]. In particular, the electrical stimulation process has been known to be more effective when engineered biomaterials such as conducting polymers, graphene-based materials, electrically active scaffolds, and fibers are used as culture platforms [9, 11, 24, 25]. Some of the examples include the use of electric field stimulation on human mesenchymal stem cells cultured on conducting polyaniline deposited with gold nanoparticles to elicit different stem cell responses [10]. It was observed that a DC field of 100 mV/cm induced the cells on these substrates to commit to neuronal cell lineage, whereas using a pulsed field of identical strength with a frequency of 1 Hz and 10% duty cycle, the stem cells showed signs of differentiation towards cardiomyocytes. In addition, stem cell differentiation towards osteogenic lineage has been shown on multiple substrates under the influence of low-strength electric (10 V/cm) and magnetic fields (100 mT) [26,27,28]. Similar cases of the dependence of stem cell response on electromagnetic field parameters are reported extensively in the literature [29,30,31].

It is clear that the electric fields have various effects on biological material (cells and tissues) and corresponding applications in regenerative therapies. However, a consistent trend that has been identified is that the field parameters must be carefully chosen to elicit the most appropriate cell response. This issue has been addressed for pulsed electric fields in the review by Weaver [32]. It is observed that exposure time has a significant effect on the cell response in addition to the electric field intensity. The studies involving increase in proliferation or change in differentiation behavior fall under the category of low field (< 100 V/cm), high exposure time (> 1 s) stimulation, and high fields (> 1 kV/cm) with high exposure time (> 1 ms) that caused cell/tissue death due to necrosis. There exists a middle ground when high fields are used with low exposure times leading to electroporation. This causes a sudden increase in the permeability of the cell membrane due to rupture and can either lead to reversible (pulse duration < 1 ms) or irreversible (pulse duration > 1 ms) electroporation leading to apoptosis/necrosis and has been shown to cause preferential killing of cancerous cells, revealing the potential applications in cancer treatment. The application of external E-field also finds relevance in medicine in the form of gene therapy, drug delivery, electro-chemotherapy, transdermal delivery of cancer drugs, and gene delivery in tissue engineering [5, 33,34,35]. Considering the various applications of E-field in the context of regenerative engineering, it is essential to understand the basis of cell-electric field interactions with a firm theoretical background and necessary experimentation.

The concept of an electrical equivalent circuit for a biological cell was first introduced for neurons by Hodgkin and Huxley [36]. While the Hodgkin-Huxley model of a simple RC network allows one to better approximate the electrical response of the neurons due to their geometry (length ≫ width), it cannot be used for other cell types. Hence, this model was further extended to a general cell type considering the cell/nuclear membrane as capacitors and cytoplasm and nucleoplasm as conducting entities(resistors) [37]. Also, the cell was modeled as a simple dielectric shell with cell membrane and cytoplasm as the only electrical entities. Here, the time constant for cell is same as the time constant for the plasma membrane, which is the product of equivalent resistance and capacitance of the network. In a similar line, Deng et al. [38] suggested an RC circuit as electrical analogue of cell. In a follow-up simulation study, Ellappan and Sundararajan [39] suggested an equivalent circuit by considering the plasma membrane as leaky dielectrics instead of ideal capacitive elements. In their transient analysis, the response of the cell model in presence of external stimulus was examined at different frequencies and the effect of parameters such as membrane resistance and capacitance was studied. The study also indicated that higher frequency signals lower the transmembrane potential, which agrees well with theoretical predictions made by considering the electrodynamic problem of a cell in the presence of electric field [40, 41].

In earlier studies from our research group, we have calculated the time constant of two different electrical analogues of biological cells by considering the cell and nuclear membranes as capacitive elements. For both models, the time constant was determined to be 2–3 μs [42]. The implications of the study were discussed in terms of the variation of time constant with different parameters such as cell size, membrane resistance, and capacitance as well as with different nucleus to cell size ratios. Further, a stochastic analysis of these models was carried out to examine the effect of the prevalent random variations in electrical parameters of cell on time constant. Interestingly, it was observed that variations in nuclear membrane capacitance had a greater impact on the time constant compared to other electrical properties of the cell. However, in the analytical study by Dubey et al., [43] considered the cytoplasm and nucleoplasm as conducting entities, whereas the conductivity of the cell/nuclear membrane was neglected. It was, therefore, considered that the cell/nuclear membranes are barriers for transportation of intracellular/extracellular ions across the cell/nucleus, which does not reflect the properties of the membrane accurately. Due to the presence of various voltage-gated channels as well as the ion pumps, the ions such as Na+, Ca2+, and K+ can be transported across the cell membrane. Hence, cell/nuclear membranes under physiological conditions have a non-zero conductivity.

Therefore, to understand the cell-electric field interaction at a finer scale, it becomes necessary to have an estimate of the values of current across cellular ultrastructures such as cytoplasm, nucleoplasm, and cell/nuclear membrane. In view of above, the present work reports the effect of amplitude, frequency, and pulse shape of the externally applied electrical stimulus on the current across various circuit components such as cell/nuclear membrane capacitance and cytoplasm/nucleoplasm resistance in the model. In the present study, the cell and nuclear membranes are considered as conducting entities. Together with our earlier analytical works [14, 17, 43], we present here the results of our analyses of a refined model of electrical analogue of the biological cell to better understand the response of a single cell towards external electrical field stimulation.

Model Description

In order to approximate the complex dynamic behavior of a cell, a relevant set of assumptions were made in devising the electrical analogue of a biological cell. The present work considers our previously stated assumptions [43]. The assumptions of analytical model described in the present study are reiterated as follows: (a) a near spherical nature of the cell and nucleus is considered; (b) the resistivity and the capacitance per unit area of the cytoplasm and nucleoplasm are considered to be identical; (c) although the biological cell contains various organelles, only the presence of the nucleus is considered; (d) the analysis is carried out assuming that cell functionality is normal, i.e., electroporation has not yet taken place; (e) the membranes are treated as both capacitive and resistive.

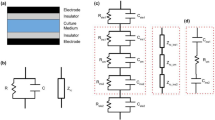
The schematic of a biological cell is shown in Fig. 1a. This schematic is subsequently used to design the electrical analogue as shown in Fig. 1b, which represents a refined model of the electrical circuit, proposed earlier by Ellappan and Sundararajan [39]. Here, the membrane bio-electrical characteristics have been described by a RC network considering the possible paths through which charge transfer can take place. The voltage-gated channels in the plasma membrane have been represented by a DC source Em in series with the membrane capacitance and resistance. The resistors R2 and R9 represent the cell membrane resistance, and R5 and R7 the nuclear membrane resistance. The resistance of the cytoplasm is represented by R3, R8, and R4 and the nucleoplasm resistance by R6. The capacitors Cm and Cn represent cell and nuclear membrane capacitances, respectively.

Fig. 1
figure 1

a A schematic of a biological cell and b its electrical equivalent considering membranes as dielectrics with non-zero conductivity and cytoplasm and nucleoplasm as conducting media

Full size image

SPICE Simulations

The electrical equivalent of a biological cell, as shown in Fig. 1b, was further analyzed using SPICE simulation package, since theoretical calculations become increasingly complex when the input is a non-steady-state signal. Also, the currents through various circuit components would require the solution of an equation like the one in Eq. (13). The versatility of the SPICE simulation package allowed us to choose customized input signal with various parameters like pulse width, offset, amplitude, frequency, and rise and fall times in a controlled manner, which in turn enabled us to record the current values for various input signals. The output response of the electrical equivalent of the biological cell was obtained by subjecting it to various electrical stimuli with different amplitudes, frequencies, and shapes. These stimuli were mainly pulses (triangular and square) and sinusoidal waveforms. The currents through the membranes (both cell and nuclear) were recorded for each signal since the transfer of ions in and out of the cell/nucleus through the membranes is the key to understand the cell fate processes. In the following, the effects of externally applied electrical stimulus on the current through the cell and nuclear membranes are analyzed in terms of pulse shape, amplitude, and frequency as well as cell size.

Results and Discussion

In general, the description of electric field interaction with biological cell is understood with the help of a standard electrodynamic setting involving Laplace equation (∇2ϕ = 0), simple cell shapes, and the analytical determination of transmembrane potential (Vm) [44] as changes in Vm cause many of the cellular responses such as electroporation, apoptosis, differentiation, and proliferation [4, 45, 46]. However, this process becomes immensely complex when major cell organelles like nucleus and mitochondria are considered. Moreover, the determination of current densities in intracellular regions becomes cumbersome with the theoretical model. In order to overcome this, RC model has been used in several studies to obtain useful parameters for quantifying cellular response to externally applied electric fields. One of the initial attempts towards a RC model for a cell was made by Gowrishankar and Weaver [47], where a RC lattice was constructed based on data obtained from whole cell clamping experiments to model the conductive and dielectric responses of cell to electric field. The model was based on the experimental data, which was applicable to irregular cell shapes and extendable to multicellular and tissue model. The main concept of the model was the description of the charge transport in the culture media and within the cell through active and passive electrical elements to obtain a complete picture of cell response to electric field. However, this was a numerical model which required computational tools to solve for nodal potentials and current densities. A simplified single-cell model, used by Ellapan and Sundarajan [39], simulated the response of single cell to electrical inputs of various frequencies in terms of the transmembrane potential. Several studies have also used RC models for cells to understand the dynamics of membrane electroporation [38, 48]. The current study is built upon the previous RC models for single cells by considering membranes as leaky dielectrics and the introduction of voltage-gated channels modeled as DC voltage sources in the RC network. The characteristic time constant of this network has been determined along with its current response to various electric signals such as square pulse, triangular pulse, sinusoidal signal, and DC signal through PSPICE simulation package. The significance of the time constant and the current response of the network have been discussed in the biophysical context.

Determination of Time Constant

The time constant of the circuit, shown in Fig. 1b, has been calculated by analyzing the circuit using Kirchhoff’s network laws. These laws are based on the fundamental principles of energy and charge conservation applied to an electrical network. Kirchhoff’s voltage law states that in a closed circuit loop, the net change in the potential is zero, a statement equivalent to the conservation of energy. Kirchhoff’s current law states that the sum total of all the currents at a node is zero, implying that the sum of currents entering and leaving a node is always zero. These laws are generally used to solve the network by determining currents and potentials in all branches of the network, and similar procedure has been followed in the present work.

In reference to Fig. 1a and considering the loop DEGFD, one can obtain

$$ \frac{1}{C_m}\int {i}_1 dt=\left({i}_0-{i}_1\right){R}_2 $$
(1)

On differentiating Eq. (1), we get

$$ \frac{i_1}{C_m}=\frac{d\left({i}_0-{i}_1\right)}{dt}{R}_2 $$
(2)

From the loop JNKJ, we have

$$ \frac{1}{C_n}\int {i}_3 dt={i}_4{R}_5 $$
(3)

Similarly, differentiating Eq. (3), we get

$$ \frac{i_3}{C_n}=\frac{d{i}_4}{dt}{R}_5 $$
(4)

The loop HJNQLPH gives

$$ \left({i}_0-{i}_2\right){R}_4={i}_2{R}_6+2{i}_4{R}_5 $$
(5)

Differentiating (5), one can obtain

$$ \frac{d{i}_0}{dt}=\frac{di_2}{dt}\left(1+\frac{R_6}{R_4}\right)+2\frac{R_5}{R_4}\frac{d{i}_4}{dt} $$
(6)

At node J, the law of conservation of charges (Kirchhoff’s current law) gives

$$ {i}_2={i}_3+{i}_4 $$
(7)

From Eqs. (6) and (7), we get

$$ \frac{d{i}_0}{dt}=\frac{di_3}{dt}\left(\frac{R_6}{R_4}+1\right)+\left(\frac{R_6}{R_4}+2\frac{R_5}{R_4}+1\right)\frac{di_4}{dt} $$
(8)

Using Eqs. (4), (8) can be written in terms of i4 as

$$ \frac{di_0}{dt}={C}_n{R}_5\left(1+\frac{R_6}{R_4}\right)\frac{d^2{i}_4}{dt^2}+\left(\frac{R_6}{R_4}+2\frac{R_5}{R_4}+1\right)\frac{di_4}{dt} $$
(9)

From the loop ADFJKQMSTWA, the conservation of energy gives

$$ \frac{2}{C_m}\int {i}_1 dt+\frac{2}{C_n}\int {i}_3 dt+{i}_2{R}_6+{i}_0\left({R}_3+{R}_8\right)-V=0 $$
(10)

Differentiating (10), we get

$$ 2\frac{i_1}{C_m}+2\frac{i_3}{C_n}+{R}_6\frac{di_2}{dt}+\left({R}_3+{R}_8\right)\frac{di_0}{dt}=0 $$
(11)

The node equation at J in terms of i4 will be

$$ {i}_2={R}_5{C}_n\frac{di_4}{dt}+{i}_4 $$
(12)

Using Eqs. (11) and (4) in (10), we have

$$ 2\frac{i_1}{C_m}+\frac{di_4}{dt}\left(2{R}_5+{R}_6\right)+{R}_6{R}_5{C}_n\frac{d^2{i}_4}{d{t}^2}+\left({R}_3+{R}_8\right)\frac{d{i}_0}{dt}=0 $$
(13)

Using Eqs. (13), (8), and (2), we get a third-order differential equation in terms of i4:

$$ \frac{d^3{i}_4}{d{t}^3}\left[\frac{C_m{C}_n{R}_5{R}_6{R}_2}{2}+\frac{C_m{C}_n{R}_5{R}_2}{2}\left(1+\frac{R_6}{R_4}\right)\left({R}_3+{R}_8\right)\right]+\frac{d^2{i}_4}{d{t}^2}\left[\frac{R_5{R}_6{C}_n}{2}+\frac{C_n{R}_5}{2}\left(1+\frac{R_6}{R_4}\right)\left({R}_3+{R}_8\right)+{R}_2{R}_5{C}_n\left(1+\frac{R_6}{R_4}\right)+\frac{C_m{R}_2}{2}\left(\frac{R_6}{R_4}+2\frac{R_5}{R_4}+1\right)\left({R}_3+{R}_8\right)+\frac{C_{\mathrm{m}}{R}_2}{2}\left(2{R}_5+{R}_6\right)\right]+\frac{di_4}{dt}\left[\frac{2{R}_5+{R}_6}{2}+\frac{1}{2}\left(1+\frac{R_6}{R_4}+2\frac{R_5}{R_4}\right)\left({R}_3+{R}_8\right)+{R}_2\left(1+\frac{R_6}{R_4}+2\frac{R_5}{R_4}\right)\right]=0 $$
(14)

The above equation is of the form

$$ a\frac{d^3{i}_4}{dt^3}+b\frac{d^2{i}_4}{dt^2}+c\frac{di_4}{dt}=0 $$
(15)

where a, b, and c are the coefficients of the third, second, and first time derivatives of “i4” respectively.

$$ a=\left[\frac{C_m{C}_n{R}_5{R}_6{R}_2}{2}+\frac{C_m{C}_n{R}_5{R}_2}{2}\left(1+\frac{R_6}{R_4}\right)\left({R}_3+{R}_8\right)\right] $$
$$ b=\left[\frac{R_5{R}_6{C}_n}{2}+\frac{C_n{R}_5}{2}\left(1+\frac{R_6}{R_4}\right)\left({R}_3+{R}_8\right)+{R}_2{R}_5{C}_n\left(1+\frac{R_6}{R_4}\right)+\frac{C_m{R}_2}{2}\left(\frac{R_6}{R_4}+2\frac{R_5}{R_4}+1\right)\left({R}_3+{R}_8\right)+\frac{C_m{R}_2}{2}\left(2{R}_5+{R}_6\right)\right] $$
$$ c=\left[\frac{2{R}_5+{R}_6}{2}+\frac{1}{2}\left(1+\frac{R_6}{R_4}+2\frac{R_5}{R_4}\right)\left({R}_3+{R}_8\right)+{R}_2\left(1+\frac{R_6}{R_4}+2\frac{R_5}{R_4}\right)\right] $$

By making the substitution, x = di4/dt, we get

$$ a\frac{d^3{i}_4}{dt^3}+b\frac{d^2{i}_4}{dt^2}+c\frac{di_4}{dt}=0 $$
(16)

with x = exp(λt), one can find the two roots of the equation λ1 and λ2 from which the time constants of the equivalent circuit of a biological cell can be obtained from the equation

$$ a{\lambda}^2+ b\lambda +C=0 $$
(17)

Since both λ1 and λ2 are roots of Eq. (17), the final expression for i4 will be a linear combination of the two solutions of the form

$$ {i}_4=A\ \exp \left({\lambda}_1t\right)+B\ \exp \left({\lambda}_2t\right) $$
(18)

Kirchhoff’s current law at the node A gives, i = i0 + i′. Since the potential V is constant, the current through the capacitor Ce is zero. This gives the current through the resistor R1 to be i' = V/R1, which is also a constant. Therefore, the total current through the circuit is also of the form of Eq. (15) and the time constants for the equivalent circuit, τ1 and τ2, can be obtained by comparing the current equation of the form (15) with a general equation used to describe R-C circuits, which is i = i(0)exp(− t/τ). This yields two values of time constants, − 1/λ1 and − 1/λ2. To calculate λ1 and λ2, we need to use the resistance and capacitance values of the cell membrane, nuclear membrane, cytoplasm, and nucleoplasm [49]. These values (R5 = 600 MΩ, R6 = 12.5 kΩ, R2 = 100 MΩ, R3 = R8 = 12.5 kΩ, Cm = 9.6 nF, Cn = 4.8 nF, and R4 = 12.5 kΩ) were taken from our earlier work as well as from the work of Ellappan and Sundararajan [39, 43]. Substituting these values, the parameters a, b, and c and, subsequently, the time constants, τ1 = 260 μs and τ2 = 34 μs, are determined.

The lesser value of time constant in more relevant to the biological processes in the context of electric field stimulation as experimental studies suggests that the membrane time constant is in the range of a few microseconds to tens of microseconds depending on the cell type [50]; hence, the other time constant (260 μs) will be neglected in further discussion. Here, it is worthwhile to mention that the time constants of the equivalent circuit of a biological cell, when considering various ionic channels/pathways at cell/nuclear membranes, are significantly larger than our earlier reported values of the time constants, 3.26 and 1.55 μs [43]. Such a difference is due to the fact that inherent resistivity of both the cell and nuclear membranes were not considered in our earlier work. The additional resistances, as considered in the present model, appear to make a biological cell slower in terms of response to the externally applied electrical stimulus, i.e., longer response time. Based on the above treatment, it is clear that a single biological cell would respond to external E-field in sub-millisecond timescale. This calculation, therefore, provides a guideline to select the pulse width to excite a single cell. However, the influence of pulse shape cannot be predicted from the above analytical model. Also rigorous would be the determination of currents through the membranes, which requires a complete analytical solution of Eq. (16) subjected to a set of initial and boundary conditions. In addition, the response time of a cell population in culture medium would require further refinement of the model described here. In the above perspective, SPICE simulations were carried out to address some of these issues.

Significance of Time Constant of RC Network

Cell electroporation is known to be a membrane phenomenon, where the application of external electric field leads to charge build-up at the plasma membrane and a high enough field strength leads to dielectric breakdown or permeabilization of the lipid membrane [51]. The timescale of this process depends upon the electrical properties of the cell and on the external electric field. Based on the timescale of the electric field stimulus, the permeabilization of the membrane can be either temporary (reversible electroporation) or permanent (irreversible electroporation). For example, intense (MV/m) nanosecond (10–100 ns) electric pulses have been known to cause apoptosis (programmed cell death) with potential biomedical applications in cancer and tumor treatment [52]. Nanosecond electric field pulses with moderate strength (10–100 kV/m) can induce reversible electroporation in cells, which can be used for drug/gene delivery and is also known to affect sub-cellular structures [53], while microsecond and moderate electric field strength pulses can cause irreversible electroporation [38]. It is therefore suggested that the response of the cell to electric field depends on both the strength of the electric field and the duration of exposure. The variations in these two parameters have been shown to yield various cellular responses [54].

In this regard, the time constant for the RC network provides useful insight into the timescale of cell responses to electric field. Earlier studies on RC model of a single cell considered cell membranes to be an ideal capacitor [43], and the estimates of the time constant obtained using such models have been of the order of 1 μs. Even though membranes are now considered leaky capacitors (dielectrics with a non-zero electrical conductivity), the time constant for the membranes derived from the simple RC model agrees with experimental studies involving sub-microsecond imaging of transmembrane potential after electrical stimulation [55]. In the present study, consideration of voltage-gated channels and membranes as leaky dielectrics has given a much higher estimate of time constant of ≈ 30 μs. This indicates that the time constant in the present model does not correspond to the charging of the plasma membrane; rather, it is indicative of the time required for the whole cell to respond to the DC electric field signal. In other words, electric signals with pulse widths much lesser than the above value (< μs) will affect the intracellular organelles while the cell membrane remains intact as seen from the greater current through nuclear membrane in the case of square pulse electric field (Fig. 3). It is also known that the cell response depends on the shape of the electrical signal used to stimulate the cell [56]. In the current study, DC signal is chosen for determining the time constants and time varying signals have been used to determine the currents in view of the fact that in vitro experiments use such electric field stimulus to obtain various cell responses on biomaterial substrates. The time constants predicted here are expected to provide a useful guide as to the timescale of possible cellular effects due to DC electric field stimulation, while the estimates for current values presented in the subsequent section serve as an indicator to the effective ion transport through the membrane.

Though the current study uses a spherical cell model to determine the time constants for the electrical equivalent, the concept itself is not limited by cell shape. The time constant of a cell is dependent on cell size, shape, and its electrical properties, and if these characteristics can be accurately known (especially the shape) for other cell types, similar models can be used to determine the time constants, as the spherical cell approximation is used only to determine the membrane capacitance and resistance. As an example, one of the first electrical models for cells, the Hodgkin-Huxley model for neurons, was a much simpler model compare to the one used here. This is due to the typical morphology of the neurons which can be described in mathematical jargon as a cylinder with length much higher than its radius, making the determination of electrical properties simpler. For other irregular-shaped cells, a parameter called shape factor is generally needed to describe its deviation from spherical nature in order to obtain the electrical properties accurately. Moreover, when irregular shapes are considered, numerical methods are necessary to completely solve the system [57]. Hence, the spherical nature considered here is to generalize the concept and make the calculations simpler.

Current Response of RC Network Through SPICE Simulations

Effect of Pulse Shape

The effect of different pulse shapes of applied input voltage on the current through cell and nuclear membrane capacitance is shown in Fig. 2. It is evident from Fig. 2 that output current through the membranes for a particular signal (sinusoidal, square, or triangular) has similar values. However, for the constant voltage (DC, 1 V), the current through the cell membrane is higher than that of nuclear membrane. In our earlier work, we optimized the voltage for enhanced cell proliferation on biomaterial surfaces to be about 1 V [17], which is the reason the present analysis was carried out with 1 V as amplitude to observe the effect of pulse shape at machine frequencies.

Fig. 2
figure 2

Effect of pulse shape on the capacitance current through the cell and nuclear membranes. For all the pulse shapes, the amplitude 1 V of the externally applied potential and 50 Hz as the frequency of sinusoidal waveform were chosen

Full size image

A comparison of the current values through the membrane resistor and capacitor for various input signal shapes is shown in Table 1. Due to the membrane capacitance, the DC signal encounters a high reactance, which is reflected in lower values for membrane capacitance current. The square pulse, which is a Heaviside step function, has the least reactance and hence has the highest current which is orders of magnitude greater than the current when a DC signal of the same strength is applied. The maximum current through the membrane capacitors, given in Table 1, is directly proportional to the extent of variation in the input signal with respect to time, i.e., to the time derivative of the input signal. For a sinusoidal signal (of 50 Hz), the derivative is lesser than for a triangular pulse (rise time and fall time 100 ns), which is lesser than that of a square pulse. The maximum current through the capacitors follows a similar trend with square pulses resulting in the highest current (0.8 mA) and DC signal (time derivative is zero) giving the lowest current (0.3 pA), summarized in Table 1 and Fig. 2. The effect of applied voltage pulses of various shapes on current through the cell and nuclear membranes is illustrated in Fig. 3. The current signals clearly indicate the dependence on the time derivative of input voltage signal. The square pulse, due to its low rise time and steep increase in the signal amplitude, results in the highest membrane capacitor current with the spike in the current profile similar to a δ-distribution (Fig. 3b). The triangular pulse, which has a constant slope due to its finite rise time, has a plateau in its current response (Fig. 3c). The current through the nuclear membrane capacitor is higher for the sinusoidal and triangular pulses because of its lower capacitance. With a square input pulse, the current through the cell membrane capacitor has a higher value compared to that of nuclear membrane capacitance because of the higher cell membrane capacitance. The square pulse behaves as a DC signal (dV/dt = 0) for the applied pulse width. However, due to the steep rise and fall of the pulse, the cell membrane capacitance will have a higher current, when compared with the triangular pulse and sinusoidal signal input.

Table 1 A summary of current through cell and nuclear membranes for various input signals as estimated by SPICE
Full size table
Fig. 3
figure 3

Effect of pulse shape on the current profiles through cell and nuclear membranes (capacitor) obtained by SPICE simulations for inputs a sinusoidal signal, b square pulse, and c triangular pulse

Full size image

The effect of different pulse shapes used to stimulate cells is evident from experimental results. Recent studies report distinct differentiation response when pulsed electric fields (differentiation of stem cells towards cardiomyocytes) and DC electric fields (neurogenic/osteogenic differentiation) are used on stem cells cultured on engineered biomaterial substrates [10]. Similarly, it has been shown that low-strength AC electrical stimulation on conducting substrates can also direct stem cell differentiation towards osteogenic cells [9, 24]. These studies show that pulse type plays an important role in directing cell response. Generally, pulsed and AC electric fields are found to be more efficient in stimulating cell populations compared to DC fields. This is thought to be due to the increased flow of charges (current) through the membrane results in signaling cascades that determine the response of the cell towards that particular stimulating signal. Moreover, pulse and sinusoidal signals reduce the resistive heating and electrode reactions in the culture system and hence the preferred option for electrical stimulation of biological cells.

Effect of Pulse Amplitude and Frequency

The effect of amplitude and frequency of the input signal was evaluated using SPICE simulation. For a sinusoidal input, the currents through both the capacitors (cell and nuclear membranes) vary linearly with frequency and amplitude. The effect of amplitude was studied at f = 50 Hz. In case of square and triangular pulses, only the effect of amplitude, rise time (tr), and fall time (tf) of the signals was seen on the maximum current through the capacitors, while the frequency of the pulses did not have any effect on the maximum current. The currents through the cell and nuclear membrane resistances are orders of magnitude greater than the current through the respective capacitances for sinusoidal and DC input signals (Table 1). This is attributed to the fact that both cell and nuclear membranes possess ion channels as well as pore structure, which make them semi-permeable to various ions and biological molecules. However, square input signal result in a comparatively higher current through membrane capacitances than the membrane resistance as the capacitive reactance is lower for a pulse signal. It is also seen that the current through nuclear membrane is lesser than that of the current through the cell membrane. The effect of amplitude/field strength can be assessed in a straightforward manner in electric field stimulation experiments. As indicated earlier, at a high enough electric field, the membrane undergoes rupture (electroporation) and eventually goes into apoptosis/necrosis. At low-strength electric fields, the behavior is different in that some cells show a positive response in a particular range of electric fields while others either show no response or show a negative response. This aspect is known to be cell type dependent, while there are hypotheses regarding how electric field stimulation on cells induces differentiation (regulation of cytoskeletal tension, Rho signaling) [58], and no consensus has been reached as to why different cell types react in distinct manner when exposed to the same electric field.

Effect of Cell Size

In view of dynamic variation in cell size due to various cellular adaptation processes particularly during cell-material interaction, the effect of variation in cell size on the current through cell membrane was studied. Depending on the cell type and the physiological conditions, the membrane resistivity value has been reported to vary between 100 and 10,000 Ω cm2 [59]. The change in the membrane resistivity values drastically affects the membrane potentials [60]. However, the present analysis considered the membrane resistivity (ρm) to be 10,000 Ω cm2 as it is more relevant to cells with spherical/spheroidal shapes [40].

Assuming the cell to be a sphere of radius r0, the resistance of the cell membrane would be

$$ {R}_m=\frac{\rho_m}{4\pi {r}_0^2} $$
(19)

The variation in the cell membrane resistor current values with the cell size is shown in Fig. 4. A non-linear variation in current through cell membrane is expected as the cells grow in size. For the realistic cell size variation in the range of 10–40 μm during the cell-material interaction, a non-linear increase of current from below 5 μA to around 30 μA has been estimated (see Fig. 4). Such an increase in the membrane current would therefore indicate that more ions or charged biological molecules can be transported across the cell membrane, as a cell would expand on a biomaterial substrate. Such increased transport would also favor various biophysical processes of the cell with the extracellular environment. The above discussion therefore indicates that atrophy/hypertrophy will have indirect influence on the response time of a biological cell to electrical stimulus. Also, the current through the membrane capacitance exhibited a similar behavior (not shown).

Fig. 4
figure 4

Variation of current through cell membrane resistance with cell size, as estimated using SPICE

Full size image

Electric Field Stimulus in Regenerative Medicine

As mentioned earlier, electric field stimulation has a wide range of applications in tissue engineering and regenerative medicine. Unlike endogenous electric fields which play an important role in wound healing and maintenance of cell homeostasis, externally applied electric fields can elicit a broader range of responses by the choice of field parameters such as intensity, frequency, and pulse shape. For example, electroporation experiments usually carried out with high electric fields and alternating/pulse fields to prevent joule heating effects have been demonstrated to have useful applications in tumor inhibition by arresting cell proliferation [61]. While the cellular responses also depend on exposure time in addition to field intensity and pulse shape, it is generally accepted that short-term exposures can enhance cell proliferation whereas longer exposure times can cause significant DNA damage, which is sometimes irreversible leading to cell apoptosis [62]. However, the field intensity examined in the present work is more applicable in the context of beneficial applications of electric field stimulus such as in tissue engineering and regenerative medicine.

Several studies have shown that a low-intensity electric field similar can induce better cell growth on biomaterial substrates, in vitro [63]. Apart from cell proliferation, low-intensity electric fields (DC/AC/pulsed) have been shown to enhance stem cell differentiation into bone-like cells, neurite outgrowth indicating differentiation towards nerve-like cells, and in some special cases such as using a low-intensity low-frequency pulsed field, stem cells have been observed to undergo cardiomyogenesis [21]. While the mechanism of action of electric field on cells is not entirely clear, some studies point towards the changes in Ca2+ influx due to electric field stimulus [64], while others indicate that complex signal transduction pathways [65], including mechano-transduction through cytoskeletal reorganization [66], are the major mechanisms for cellular responses to external electrical stimulus. Though the mechanism is unclear, the present work adds to the theoretical foundation developed so far on the interaction between cells and electric field with a simplified R-C network perspective.

Conclusions

In this work, both analytical calculations and simulation studies have been performed to understand both the qualitative and quantitative aspects of interaction of E-field with a biological cell. In particular, calculations were used to determine the time constant for the electrical analogue of the cell. The following key conclusions emerge:

  1. (a)

    The analytical solution of a complex electrical analogue circuit of a biological cell reveals that the response time of a biological cell is sub-millisecond (τ2 ≈ 30 μs). This value, however, is an order of magnitude higher than that estimated in our previous work. It can be rationalized from the fact that in the present work, we consider the presence of various ion channels on the cell membrane as well as nuclear pore complexes on the nuclear membrane and such important pathways which were neglected in our earlier work.

  2. (b)

    SPICE simulations were performed to determine the external field-induced cell and nuclear membrane currents. The present study provides evidence that the cell membrane allows more current than nuclear membrane, i.e., the cell membrane can transport more ions or charged species across it than nuclear membrane.

  3. (c)

    The influence of cell size indicated that the membrane current increases as the cell size increases, due to increased membrane surface area, thereby decreasing the effective resistance implying that it is easier to electroporate larger sized cells.

  4. (d)

    It has been clearly observed that the shape of the input pulse signal strongly affects the currents through the cell and nuclear membrane capacitances. Both the amplitude and frequency have a linear effect on the currents through the cell components in the electrical equivalent circuit. In addition, the rise and fall times of the applied signal play an important role in affecting the current through cell and nuclear membrane capacitances.