Nonlinear Modeling, Analysis and Simulation of Wind Turbine Control System With and Without Pitch Control as in Industry

Abstract

This chapter introduces the state-of-the-art modeling, analysis and simulation of the wind turbine dynamics and control. The modeling part is a comprehensive time domain layout of the model currently considered by industry, such as General Electric, National Renewable Energy Lab and other major manufacturers. The time domain modeling allows for nonlinear and optimization studies for the highly nonlinear and complex wind turbine control system. Also, this allows for better understanding and intensive study of the very important Pitch control, which is crucial in wind turbine systems, for building/designing control strategies and for optimization objectives. This chapter also provides a documentation for what have been published recently (2016–2018) regarding important dynamical properties and parameter sensitivities in the wind turbine control system. In this regard, the chapter also provides a possible reduction to the wind turbine control system based on the range of wind speeds the wind turbine is exposed to. This allows scholar to study the wind turbine dynamics and control in three different regions, one of them has the Pitch control activated in the case of higher wind speeds. Moreover, the chapter provides an illustration of the dynamical stability and the possibility of approximating the wind turbine control system by multiple time scales. Additionally, The chapter provides different simulations of the system, which can be helpful for academic studies that intend to run non-autonomous scenarios. Also, we cite in a recently (2018) published work, a data validation for the model versus real measured data of the power-wind curve, which magnify the findings of our study.

List of Symbols  

$P_{wind}$ :

wind power in the airstreams

$\rho , A_r, v_{wind}$ :

air density, rotor area (m$^2$), wind speed (m/s)

$C_p, P_{mech}$ :

aerodynamic power coefficient, power extracted by the turbine

$w_{ref}, P_{elec}$ :

rotor reference speed, electrical (active) power delivered to the grid

V :

the magnitude of the terminal voltage

R, X, E:

infinite bus parameters: resistance, reactance, infinite bus voltage

$Q_{gen}$ :

total reactive power delivered to the grid

$H, H_g$ :

turbine and generator inertia constants

$w_0, w_{base}$ :

initial speed, base angular frequency

$D_{tg}, K_{tg}$ :

shaft damping and stiffness constants

$f_1, f_2$ :

integrals of differences of speeds and powers

$P_{stl},K_{pp}$ :

rated power and Pitch control proportional

$K_{ip},K_{pc}$ :

integral gain and Pitch compensation proportional

$\theta ,K_{ic}$ :

Pitch angle and integral gain

$p_{inp},T_{pc}$ :

power order (subject to modifications) and its time constant

$K_{ptrq},K_{itrq}$ :

torque control proportional and gain

$P_{1elec},T_{pwr}$ :

filtered electrical power and its time constant

$V_{ref},K_{Qi}$ :

reference voltage and its gain

$E_{qcmd}, K_{vi}$ :

reactive voltage command and terminal voltage control gain

$Q_{droop},T_{lpqd}$ :

the droop function and its time constant

$Q_{inp}$ :

the input to the droop function block

$V_{1reg}, T_r$ :

filtered supervisory voltage and its time constant

$V_{reg}, T_r$ :

supervisory voltage and its time constant

$Q_{wvl}, Q_{wvu}, K_{pv}, K_{iv}$ :

two integrals lead to $Q_{ord}$ and their gains

 

1 Brief Introduction

Humanity future is depending much on advancement and development of renewable energies. There are many reasons of why we need to expand our energy systems. This is due to economic justifications and environmental concerns. No matter what the reasons are, we require additional understanding of the generation of renewable energies if we are to fully utilize them.

Based on the US department of energy reported [1], wind energy is the fastest growing source of renewable energies. Consequently, we need more studies and research and to fully comprehend the dynamics and behavior of Wind Turbine Generators (WTGs) if we are to gain the most from this valuable resource. Both corporations and governments are highly interested in understanding the challenges of integrating WTGs with other conventional power systems. Because of the complexities involved in the WTGs implementation, researching control systems, optimization, energy storage, and power generation of WTGs has dramatically increased recently. In this regard, this chapter is intended to provide a state-of-the-art comprehensive modeling effort that should guide scholars working in the research areas mentioned earlier in this paragraph.

The provided modeling effort in this chapter is a summary for the state-of-the-art nonlinear modeling of WTGs control system dynamics. The industry publications, namely General Electric (GE) ones [2, 3], have been intensively investigated in the last two years through the publications [4,5,6,7,8,9,10,11,12]. These studies converted the model found in GE reports into nonlinear system of differential-algebraic equations, followed by a wide range of analysis and simulation results. The resultant time domain nonlinear model can be reduced based on the wind speed $v_{wind}$ range the WTG is exposed to. This important possibility of reduction to the model, will be covered and presented collectively in Sect. 2. Also, we will summarize some of the most recent and important observations these studies have concluded about the WTG system, such as parameter sensitivity, stability and different time scale structure found in the WTG system. In Sect. 3, the Pitch control and its significance will be presented. Additionally, some non-autonomous simulations for the given model under Pitch control, is provided. In the same section, we will provide a Simulink verification of the model and how it compares to National Renewable Energy Lab [13, 14]. In this regard, it is important to mention that our modeling intensive study recognized some other modeling sources such as [15,16,17,18]. Also, at the end of this chapter, we will provide and discuss a real data validation for the power-wind curve of our model. These verifications and validations are a supportive evidence that the modeling effort presented in this chapter is reliable. This is essential in any optimization or control study. The reader is recommended to check the Ph.D. dissertation [19] for more detailed information about the topics covered in this chapter.

2 State-of-the-Art Nonlinear Modeling of WTGs

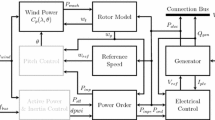
In this section, we provide a mathematical model that is in time domain (can be solved by stiff differential equations solvers such as ODE15s in Matlab). This full scale modeling allow for better and more in-depth control studies. This is especially true because the WTG system is highly nonlinear. Also, a system/model formulated in time domain, usually provide better framework for non-autonomous simulations, keeping in mind that non-autonomous simulations are more practical to present extreme scenarios. We start by explaining the different controls in WTGs and translate them into differential equations. Then, we provide tables that summarize and collect the parameters, $C_p$ coefficients, and limiters (control limits) needed for the model. Also, we give a method to eliminate the algebraic equation resulting from the network equation. This results in a system of differential equations instead of a system of differential-algebraic equations, which allows for simpler implementation in numerical solvers.

The main references used while constructing the model are [2,3,4,5,6, 18]. In [2], the control blocks are consistent of the wind power extraction block, one/two mass block, Pitch compensation control block, and reactive power block (power factor and supervisory voltage cases). In [3], $C_p$ curves are provided and explained. The GE team suggested an extra two optional blocks to, possibly, be added (active power and inertia blocks). The GE team in [3] introduced the so called Q Droop function, which has been intensively studied in [6] and fully analyzed in [11]. The study [18] introduced their model effort citing [20] and GE studies. The reader may ask a legitimate question: Why and how GE models relate to other WTGs? In another words, how building the model is inclusive to the-state-of-the-art modeling efforts if it follows heavily GE modeling? These questions were answered by detail in [4,5,6,7,8,9,10,11]. The answers though can be grouped in the two points below:

• 1. The GE team made the case in their reports [2, 3] that their model can be used to represent WTG models for other manufacturers/companies. As a matter of fact, they have provided many validation results, as can be found in [21].

• 2. In [8], it is shown that the GE modeling is equivalent to the NREL [13] if we fix the parameters. The Simulink projects used for this comparison are also given in Sect. 3.4. Additionally, we provide in Sect. 3.4 a discussion regarding the data validation for the proposed model (uses intensively GE) versus the model of [18, 20].

2.1 Main Outline of the Model

• Wind power model: Using basic physics, the wind power in the air streams is given by $P_{wind}= \frac{1}{2} \rho A_r v_{wind}^3$ Per Unit (pu), see [3]. This block models how a WTG extracts power from the air and with what efficiency. The model’s main purpose is to introduce the $C_p$ curves such that the power extracted by the WTG is $P_{mech}= \frac{1}{2} C_p \rho A_r v_{wind}^3$. As discussed in the introduction, and as in [22], the ideal $C_p$ is the Betz limit which is approximately 0.59. No WTG can extract more than the Betz limit of the power available in the air-streams. $C_p$ curves of the three bladed wind turbine (type-3) are better other types for some tip ratios (Fig. 1).

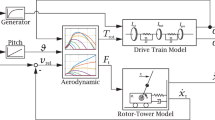
• Rotor model: This model represents the dynamics of the generator and turbine speeds due to the electrical and mechanical torques. The two-mass model has been introduced in [2, 3, 18] while in [23] this block was represented by a single-mass rotor. It can be noticed that GE studies [2, 3] hinted that single mass rotor may be used for simplification. Later (in Sect. 2.2.1) we will mention the representative differential equations for both models. Figure 2 shows the transfer function for this block as in [3].

• Reference speed: This block models how the reference speed is calculated. The reference speed dynamics are dependent on the generated electric power such that at steady state $w_{ref}=f(P_{elec})$. GE studies [2, 3] mentioned that the reference speed should increase slowly with the generated electric power until it reaches the rated speed. This speed is essential to control the generator and turbine speeds. There is a difference between [2, 3, 18] regarding the transfer function of the reference speed. Later (in Sect. 3.4) we will discuss this difference in more detail.

• Pitch control and compensation: This block captures the dynamics of the Pitch. This has been a growing area of research. This control calculates the Pitch angle based on the differences between the rated power and the power order, and between the reference speed and the generator speed. The Pitch angle has direct effect on power extraction efficiency. This is an important control to keep the WTG producing the rated power for a higher range of wind speeds. Figure 3 shows the transfer function for this block as in [3].

• Reactive power control: This control manages the generated reactive power from the WTG. This control can be in the power factor setup or the supervisory voltage setup. The first case occurs when the WTG is treated as one unit by itself, while the second case occurs when the WTG is treated as one unit in a compound of units. These two cases were introduced in [2, 3, 18]. Figure 4 shows the transfer function for this block as in [3].

• Electrical control: Unlike the previous block where the control was for the reactive branch that feeds the generator, the electrical control shows how the active current can be generated and controlled. This block is the same across the references [2, 3, 18] that covered it. Figure 5 shows the transfer function for this block as in [3].

• Active power and inertia controls: Usually these controls are not activated. The function of these two controls is to manage the power order produced by the WTG. This management depends on and corresponds to changes in bus frequency. The two controls provide extra power in the case there is lower than normal bus frequency (reference frequency) and vise versa. The active power control provide extra power by setting up the maximum rated power and cutting out, if needed, the available power to the WTG. On the other hand, the inertia control does the same function, but by providing extra power from the rotor inertia. GE [3] has hinted that most current WTGs have yet to implement these controls as of 2010. Figures 6 and 7 show the blocks as in [3].

• Converter/Generator model: This is the step where the output the WTG is delivered to the power grid. Two branches are considered in this model, active and reactive ones, which deliver the active and the reactive power to the grid respectively. In [2, 3] this model is very similar, with some lower and upper limit differences for the controls, however, in [18] we see that a third branch is added to the model for the phase shift convergence between the resultant components (current and voltage) of the wind turbine and the grid. For more detail about how this difference is insignificant when we have stability, the reader is recommended to read about the convergence between the models in [19]. Figures 8 and 9 show the generator model as in [2, 18] respectively (Fig. 10).

• Terminal voltage and grid model: The terminal voltage is the connection between the converter/generator model and the grid model. In the models we follow, the wind turbine is connected to the grid in order to work. This implies that even for theoretical/mathematical studies, the grid should be modeled so we can have an algebraic equation (the network equation) from Kirchhoff’s law, that relates the dynamics of the WTG to the grid. In our study, we follow the model used in [18] and suggested in [2, 3] to represent the grid by an infinite bus model, see Fig. 11. Therefore, the terminal voltage will be given by the following equation as in [18]:

  $$\begin{aligned} (V^2)^2-[2(P_{elec}R+Q_{gen}X)+E^2]V^2+(R^2+X^2)(P_{elec}^2+Q_{gen}^2)=0 \end{aligned}$$

  (1)

  Note that, if the grid model changes to another model other than the infinite bus, a new algebraic constraint will need to be derived and analyzed. Without this part of the grid modeling, the wind turbine is working without load and has undefined inputs to some of the control dynamics. Figure 12 gives the transfer functions of the WTG as in [3].

Fig. 1

WTG control blocks and dynamics

Fig. 2

Two mass model of a WTG as in [3]

Fig. 3

Pitch control model of a WTG as in [3]

Fig. 4

Reactive power control of a WTG as in [3]

Fig. 5

Electrical control of a WTG as in [3]

Fig. 6

Active power control of a WTG as in [3]

Fig. 7

Inertia control of a WTG as in [3]

Fig. 8

Converter/Generator model of a DFAG/DFIG WTG as in [2]

Fig. 9

Converter/Generator model of a DFAG/DFIG WTG as in [18]

Fig. 10

$w_{ref}$ steady state as a function of $P_{elec}$ as in [4]

Fig. 11

Single machine infinite bus test system as in [4]

Fig. 12

All of the WTG model transfer functions and controls as in [3]

2.2 Characteristics and Dynamical Analysis

2.2.1 Translating the Blocks of Transfer Functions and Controls into a System of Differential Algebraic Equations

Having first reviewed the transfer functions and control blocks in Sect. 2.1, we now begin the process of breaking down the blocks (in every Fig.) into algebraic relations in the transfer function domain. This will be done by deriving the transfer function relations after specifying nodes of variables.

Group 1: Two mass model as in Fig. 2.

In Fig. 2, we let the nodes $s_6=w_g$ and $s_8=w_t$, so the turbine speed will be the sum of $w_0$ and the node $s_6$. Therefore, $w_{turbine}=w_{rotor}=w_t+w_0$ and similarly the generator speed $w_{generator}=w=w_g+w_0$. Also we let $\varDelta \theta _m=s_9-s_7$, so $T_{shaft}=K_{tg}\varDelta \theta _m$. Thus $w_t$ is given by,

$$\begin{aligned} w_t=\frac{1}{2H}\cdot \frac{1}{s}[T_{mech}+D_{tg}(w_g-w_t)+T_{shaft}]. \end{aligned}$$

(2)

Similar to Eq. (2) we get,

$$\begin{aligned} w_g=\frac{1}{2H_g}\cdot \frac{1}{s}[-T_{elec}-D_{tg}(w_g-w_t)-T_{shaft}] \end{aligned}$$

(3)

and,

$$\begin{aligned} \varDelta \theta _m=\frac{w_{base}}{s}(w_g-w_t). \end{aligned}$$

(4)

The above equations contain the dynamics of the two mass rotor model.

Group 2: Pitch control as in Fig. 3.

In Fig. 3, we start with the two integrators (branches that have $\frac{1}{s}$). We let $f_1$ be the output of the transfer function $\frac{K_{ic}}{s}$ and we let $f_2$ be the output of the transfer function $\frac{K_{ip}}{s}$. Thus,

$$\begin{aligned} f_1=\frac{(w-w_{ref})}{s}=\frac{(w_g+w_0-w_{ref})}{s} \end{aligned}$$

(5)

and,

$$\begin{aligned} f_2=\frac{(P_{inp}-P_{stl})}{s}. \end{aligned}$$

(6)

The Pitch angle command ($\theta _{cmd}$) is the node after summing the upper and the lower outputs of the Pitch control. Also, it is the node before the transfer function of $T_{pl}$. Thus $\theta _{cmd}$ is given by,

$$\begin{aligned} \theta _{cmd}=K_{pp}(w_g+w_0-w_{ref})+K_{ip}f_1+K_{pc}(P_{inp}-P_{stl})+K_{ic}f_2. \end{aligned}$$

(7)

The Pitch angle ($\theta$) is the output of the transfer function of $T_{pl}$, which has $\theta _{cmd}$ as an input. Thus $\theta$ is given by,

$$\begin{aligned} \theta =\theta _{cmd}\frac{1}{1+s\cdot T_{pl}}. \end{aligned}$$

(8)

After algebraic re-arrangement we get,

$$\begin{aligned} \theta =\frac{K_{pp}(w_g+w_0-w_{ref})+f_1+K_{pc}(P_{inp}-P_{stl})+f_2}{1+s\cdot T_{pl}}. \end{aligned}$$

(9)

Equations (5), (6), and (9) contain the dynamics of the Pitch control.

Group 3: Reference speed as in Fig. 12.

The reference speed $w_{ref}$ is the output of the transfer function ($\frac{1}{1+s\cdot 60}$), which has the node symbol $s_5$ (at the upper part of Fig. 12). The input for this transfer function is $-0.75P^2_{elec}+1.59P_{elec}+0.63$. Thus $w_{ref}$ is given by,

$$\begin{aligned} w_{ref}=\frac{-0.75P^2_{elec}+1.59P_{elec}+0.63}{1+s\cdot 60}. \end{aligned}$$

(10)

Equation (10) represent the dynamics of $w_{ref}$.

Group 4: Power order as in Fig. 12.

The main power order $P_{inp}$ is the output of the transfer function of $T_{pc}$, which has the node symbol $s_4$ (in the middle of Fig. 12). The input for This transfer function is the multiplication of w and the output of the transfer function that has the node symbol $s_2$. With $f_1$ in Eq. (5) and $w=w_g+w_0$, $P_{inp}$ is given by,

$$\begin{aligned} P_{inp}=\frac{(w_g+w_0)(K_{ptrq}+K_{itrq}f_1)}{1+s\cdot T_{pc}} \end{aligned}$$

(11)

and $w_{sho}$ (the output of the transfer function of $T_w$ with the node symbol $s_{10}$) is given by,

$$\begin{aligned} w_{sho}=\frac{(P_{inp}-P_{lim})\cdot s\cdot T_w}{1+s\cdot T_w}. \end{aligned}$$

(12)

As shown at the sum after the node $s_{10}$ in Fig. 12, the final power order is given by,

$$\begin{aligned} P_{ord}=P_{lim}+w_{sho}+dpwi. \end{aligned}$$

(13)

Group 5: Reactive power in power factor setup case and electrical controls as in Figs. 4 and 5.

Since we consider the reactive power control operating in power factor case, then the lower part in Fig. 4 is operating. We let the output of the transfer function of $T_{pwr}$ be $P_{1elec}$ (see Fig. 4). Thus $P_{1elec}$ is given by,

$$\begin{aligned} P_{1elec}=\frac{P_{elec}}{1+s\cdot T_{pwr}}. \end{aligned}$$

(14)

$Q_{cmd}$ is the output of the multiplier in Fig. 4. Therefore,

$$\begin{aligned} Q_{cmd}=P_{1elec}\cdot \tan (PFA_{ref}). \end{aligned}$$

(15)

In the electrical control (Fig. 5), $V_{ref}$ is the output of the transfer function of $K_{Qi}$ (upper part of Fig. 5). This transfer function has $Q_{cmd}-Q_{gen}$ as an input. Thus $V_{ref}$ is given by,

$$\begin{aligned} V_{ref}=\frac{K_{Qi}(Q_{cmd}-Q_{gen})}{s}. \end{aligned}$$

(16)

Equations (14) and (16) contain the dynamics of group 5.

Group 6: Reactive power in supervisory voltage setup case and electrical controls as in Figs. 4 and 5.

The $Q_{droop}$ function as shown in Fig. 12 in [3] is given by,

$$\begin{aligned} Q_{droop}=\frac{(Q_{inpt}-Q_{droop})}{1+s\cdot T_{lpdq}}. \end{aligned}$$

(17)

Since we consider the reactive power control operating in supervisory voltage case, then the upper part in Fig. 4 is operating. We let $V_{1reg}$ be the output of the transfer function of $T_r$, which has the node symbol $s_3$ (see Fig. 4). This transfer function has $V_{reg}$ as an input. Thus $V_{reg1}$ is given by,

$$\begin{aligned} V_{1reg}=\frac{(V_{reg}-V_{1reg})}{1+s\cdot T_r}. \end{aligned}$$

(18)

In Fig. 4, we let $f_n=1$ or included in the gains (see page 4.7 in [3], second paragraph). We let the outputs of the transfer functions of $K_{pv}$ and $K_{iv}$ be $Q_{wvl}$ and $Q_{wvu}$ respectively. The input for those two transfer functions is $V_{ref}-V_{1reg}-V_{qd}$ (see Fig. 4). Thus $Q_{wvl}$ and $Q_{wvu}$ are given by,

$$\begin{aligned} Q_{wvl}=\frac{K_{pv}(V_{rfq}-V_{1reg}-V_{qd})}{1+s\cdot T_v} \end{aligned}$$

(19)

and,

$$\begin{aligned} Q_{wvu}=\frac{K_{iv}(V_{rfq}-V_{1reg}-V_{qd})}{s}. \end{aligned}$$

(20)

As shown in Fig. 4, $Q_{wv}$ is given by,

$$\begin{aligned} Q_{wv}=Q_{wvl}+Q_{wvu}. \end{aligned}$$

(21)

The output of the transfer function of $T_c$ is $Q_{ord}$ (see Fig. 4). The input for this transfer function is $Q_{wv}$. Thus $Q_{ord}$ is given by,

$$\begin{aligned} Q_{ord}=\frac{Q_{wv}}{1+s\cdot T_c}. \end{aligned}$$

(22)

Since the reactive power control is operating in supervisory voltage case, then $Q_{cmd}=Q_{ord}$ from Eq. (22). Equation (16) holds for this group 6 as a representative for the electrical control. Equations (17)–(20), (22), and (16) contain the dynamics of group 6.

Group 7: Active power and inertia controls as in Figs. 6 and 7.

For the active power control (Fig. 6), $P_{avf}$ is the output of the transfer function of $T_{pav}$. This transfer function has $P_{avl}$ as an input. Thus $P_{avf}$ is given by,

$$\begin{aligned} P_{avf}=\frac{P_{avl}}{1+s\cdot T_{pav}}. \end{aligned}$$

(23)

For the inertia control (Fig. 7), fltdfwi is the output of the transfer function of $T_{lpwi}$, which has the node symbol $s_{12}$. This transfer function has dfdbwi as an input. Thus dfdbwi is given by,

$$\begin{aligned} fltdfwi=\frac{dfdbwi}{1+s\cdot T_{lpwi}}. \end{aligned}$$

(24)

The final output of the inertia control (dpwi) is the output of the transfer function of $T_{wowi}$, which has the node symbol $s_{13}$. This transfer function has fltdfwi multiplied by the gain $K_{wl}$ as an input. Thus dpwi is given by,

$$\begin{aligned} dpwi=\frac{K_{wl}\cdot dpwi\cdot s\cdot T_{wowi}}{1+s\cdot T_{wowi}}. \end{aligned}$$

(25)

Equations (23)–(25) contain the dynamics of group 7.

Group 8: DFAG generator/converter as in Fig. 8.

In order to have equations for $E_q$ and $I_{plv}$ (outputs of the transfer functions with the node symbols $s_0$ and $s_1$ respectively), we need to relate $E_{qcmd}$ and $I_{pcmd}$ (inputs of the transfer functions with the node symbols $s_0$ and $s_1$ respectively) to other variables we have that represent the dynamics in other controls. Looking at the electric control (Fig. 5), we notice that $E_{qcmd}$ is the output of the transfer function of $K_{iv}$, which has the node symbol $s_1$. Similarly, in the lower part of Fig. 5, we find $I_{pcmd}$ as the output of the divider ($\frac{P_{ord}}{V}$). Thus $E_{qcmd}$ is given by,

$$\begin{aligned} E_{qcmd}=\frac{K_{vi}(V_{ref}-V)}{s} \end{aligned}$$

(26)

and,

$$\begin{aligned} E_q=\frac{E_{qcmd}}{1+s\cdot 0.02}. \end{aligned}$$

(27)

We have $I_{pcmd}=\frac{P_{ord}}{I_{plv}}$, then $I_{plv}$ is given by,

$$\begin{aligned} I_{plv}=\frac{\frac{P_{ord}}{I_{plv}}}{1+s\cdot 0.02}. \end{aligned}$$

(28)

We note that $I_p$ in [2] is equivalent to $I_{plv}$ (the symbol used in this document) in [3]. Equations (26)–(28) contain the dynamics of the generator.

After applying inverse Laplace transform to the equations above, we derive a system of differential equations as follows:

Group 1: Two-mass rotor.

$$\begin{aligned} \frac{dw_g}{dt} = \frac{1}{2H_g}\left[ - \frac{P_{elec}}{w_g+w_0}-D_{tg}(w_g-w_t) -K_{tg} \varDelta \theta _m\right] . \end{aligned}$$

(29)

$$\begin{aligned} \frac{dw_t}{dt} = \frac{1}{2H}\left[ \frac{P_{mech}}{w_t+w_0}+D_{tg}(w_g-w_t) +K_{tg} \varDelta \theta _m\right] . \end{aligned}$$

(30)

$$\begin{aligned} \frac{d(\varDelta \theta _m)}{dt} = w_{base}(w_g-w_t). \end{aligned}$$

(31)

As discussed when we were introducing the different controls, a one mass model may be used to replace the two-mass model in group 1. The one mass differential equation was given in [24]:

$$\begin{aligned} \frac{dw}{dt} = \frac{1}{H w_{base}}[P_{mech}-P_{elec}]. \end{aligned}$$

The following relations hold:

$$\begin{aligned} P_{mech}= \frac{1}{2}C_p(\lambda ,\theta ) \rho A_r v_{wind}^3= \frac{1}{2}\left( \sum _{i=0}^{4} \sum _{j=0}^{4} \alpha _{i,j} \theta ^i\lambda ^j\right) \rho A_r v_{wind}^3 \end{aligned}$$

and,

$$\begin{aligned} P_{elec}=V I_{plv}. \end{aligned}$$

Group 2: Pitch control.

$$\begin{aligned} \frac{df_1}{dt} = w_g+w_0-w_{ref}. \end{aligned}$$

(32)

$$\begin{aligned} \frac{df_2}{dt} = P_{inp}-P_{stl}. \end{aligned}$$

(33)

$$\begin{aligned} \frac{d\theta }{dt}= & {} \frac{1}{T_p}[K_{pp}(w_g+w_0-w_{ref})+K_{ip}f_1 \nonumber \\&+ K_{pc}(P_{inp}-P_{stl})+K_{ic}f_2-\theta )]. \end{aligned}$$

(34)

Group 3: Reference speed.

$$\begin{aligned} \frac{dw_{ref}}{dt} = \frac{1}{60}[-0.75P_{elec}^2+1.59P_{elec}+0.63-w_{ref}]. \end{aligned}$$

(35)

Group 4: Power order.

$$\begin{aligned} \frac{dP_{inp}}{dt}= & {} \frac{1}{T_{pc}}[(w_g+w_0)(K_{ptrq}(w_g+w_0-w_{ref}) \nonumber \\&+ K_{itrq}f_1)-P_{inp}]. \end{aligned}$$

(36)

$$\begin{aligned} \frac{dw_{sho}}{dt}= & {} \frac{dP_{inp}}{dt} -\frac{dP_{stl}}{dt} - \frac{1}{T_w}w_{sho}. \end{aligned}$$

(37)

Group 5: Reactive power control in the power factor setup case.

$$\begin{aligned} \frac{dP_{1elec}}{dt}= \frac{1}{T_{pwr}}[P_{elec}-P_{1elec}]. \end{aligned}$$

(38)

$$\begin{aligned} \frac{dV_{ref}}{dt}= K_{Qi}[Q_{cmd}-Q_{gen}] \end{aligned}$$

(39)

where,

$$\begin{aligned} Q_{gen}=\frac{V(E_q-V)}{X_{eq}}. \end{aligned}$$

$Q_{cmd}$ is explained in detail in Sect. 2.2.2.

Group 6: Reactive power control in the supervisory voltage setup case.

$$\begin{aligned} \frac{dQ_{droop}}{dt}= \frac{1}{T_{lpqd}}[Q_{inpt}-Q_{droop}]. \end{aligned}$$

(40)

$$\begin{aligned} \frac{dV_{1reg}}{dt}= \frac{1}{T_r}[V_{reg}-V_{1reg}]. \end{aligned}$$

(41)

$$\begin{aligned} \frac{dQ_{wvl}}{dt}= \frac{1}{T_v}[K_{pv}(V_{ref}-V_{1reg}-V_{qd})-Q_{wvl}]. \end{aligned}$$

(42)

$$\begin{aligned} \frac{dQ_{wvu}}{dt}= K_{iv}(V_{ref}-V_{1reg}-V_{qd}). \end{aligned}$$

(43)

$$\begin{aligned} \frac{dQ_{ord}}{dt}= \frac{1}{T_c}(Q_{wvl}+Q_{wvu}-Q_{ord}). \end{aligned}$$

(44)

Equation (39) is holding in all reactive power groups.

Group 7: Active power control and inertia control.

$$\begin{aligned} \frac{dP_{avf}}{dt}= \frac{1}{T_{pav}}[P_{avl}-P_{avf}]. \end{aligned}$$

(45)

$$\begin{aligned} \frac{d(fltdfwi)}{dt}= \frac{1}{T_{lpwi}}[dfdbwi-fltdfwi]. \end{aligned}$$

(46)

$$\begin{aligned} \frac{d(dpwi)}{dt}= \frac{K_{wi}}{T_{lpwi}}[dfdbwi-fltdfwi]- \frac{dpwi}{T_{wowi}}. \end{aligned}$$

(47)

Group 8: DFAG generator/converter.

$$\begin{aligned} \frac{dE_{qcmd}}{dt}= K_{vi}[V_{ref}-V ]. \end{aligned}$$

(48)

$$\begin{aligned} \frac{dE_q}{dt}= \frac{1}{0.02}[E_{qcmd}-E_q]. \end{aligned}$$

(49)

$$\begin{aligned} \frac{dI_{plv}}{dt}= \frac{1}{0.02}\left[ \frac{P_{ord}}{V}-I_{plv}\right] . \end{aligned}$$

(50)

Group 9: The algebraic equation resulting from the network (see [18]):

$$\begin{aligned} 0=(V^2)^2-[2(P_{elec}R+Q_{gen}X)+E^2]V^2+(R^2+X^2)(P_{elec}^2+Q_{gen}^2). \end{aligned}$$

(51)

Table 1 represents the model’s parameter values as in [3], however the grid parameter values are taken from [18]. Table 2 has the $C_p$ curves’ needed coefficients as in [3]. Also, we define the control limits introduced in [3] to be the lower and upper bounds as following in Table 3:

Table 1 The model’s parameter value

Table 2 $C_p$ coefficients $\alpha _{i,j}$

Table 3 Control limits to be applied as in [3]

2.2.2 Reduction of the Model

Here we go through a number of possible cases that reduce the system. These reductions are based on the range of wind speeds the WTG is operating on, or on which optional controls, such as active power and inertia controls are deactivated.

Wind Speeds versus Reference Speed: The rated reference speed is $w_{ref}=1.2$ pu. Physically the WTG can’t reach this rated speed with low wind speeds. That is why $w_{ref}$ increases gradually as shown in Eq. (35), until it reaches 1.2 pu. Given the model and the parameter in this study, the rated reference speed (1.2 pu) is reached at $v_{wind}=8.2$ m/s. Therefore, the differential equation of $w_{ref}$ can be seen as,

$$\begin{aligned} \frac{dw_{ref}}{dt} = \left\{ \begin{array}{ll} \frac{1}{60}[-0.75P_{elec}^2+1.59P_{elec}+0.63-w_{ref}] &{} v_{wind}< 8.2 \, \text {m/s} \\ 0, \,w_{ref}(0)=1.2 &{} v_{wind}\ge 8.2 \, \text {m/s} \end{array} \right. \end{aligned}$$

Therefore based on the above equation, Eq. (35) can be considered as part of the system’s dynamics (if $v_{wind}< 8.2$) or eliminated (if $v_{wind}\ge 8.2$) by setting $w_{ref}=1.2$.

Electric Power versus Pitch Control: Unless mentioned otherwise, the rated electric power generated is 1 pu. The Pitch control gets activated only when the WTG would otherwise generate more power than the rated power. In this case, the Pitch angle increases, so less power is extracted, and the electric power is held at the rated power. When $\theta =0$ extraction of power is maximized. Therefore the differential equation of $\theta$ can be seen as,

$$\begin{aligned} \frac{d\theta }{dt} = \left\{ \begin{array}{ll} \frac{1}{T_p}[K_{pp}(w_g+w_0-w_{ref})+K_{ip}f_1+ K_{pc}(P_{inp}-P_{stl})\\ +K_{ic}f_2-\theta )] &{} P_{elec}> 1 \, \text {pu} \\ \\ 0, \, \theta (0)=0 &{} P_{elec}\le 1 \, \text {pu} \end{array} \right. \end{aligned}$$

Therefore, based on the above equation, Eq. (34) can be considered part of the system’s dynamics (high wind speeds such that $P_{elec}> 1$) or eliminated by setting $\theta =0$ (to maximize power extraction for low wind speeds when $P_{elec}\le 1$). If we set $\theta =0$, we eliminate $f_2$ as well in Eq. (33).

Reactive Power Control $Q_{cmd}$ Cases: In the reactive power control, $Q_{cmd}$ is dependent on whether the reactive power control is operating in power factor case or supervisory voltage case. This difference was explained in group 5 and 6 in Sect. 2.2.1. We can summarize that difference in the following relation:

$$\begin{aligned} Q_{cmd} = \left\{ \begin{array}{ll} P_{1elec}\cdot \tan (PFA_{ref}) &{} \text {Power factor case} \\ Q_{ord} &{} \text {Supervisory voltage case} \\ \text {constant or considered from another model} \end{array} \right. \end{aligned}$$

The nature of the study determines the reactive power setup case (represented by Eqs. (38)–(39) in the power factor case or by Eqs. (40)–(44) and (39) in the supervisory voltage case). As mentioned in [3] it can also be a constant or from a separate model depends on the study and its conditions.

The Power Order $P_{ord}$ Cases: The power order as shown at the sum in the lower part of Fig. 12, has three main parts. Those parts are the regular power order $P_{inp}$, the effect of the active power control $w_{sho}$, and the output of the inertia control dpwi (see Eq. (13)). But the active power control and the inertia control can be activated or deactivated. This lead to $P_{ord}$ can be one of the following cases:

$$\begin{aligned} P_{ord} = \left\{ \begin{array}{ll} P_{inp} &{} \text {Active Power and inertia controls (deactivated)} \\ P_{lim}+w_{sho} &{} \text {Active Power control (activated)} \\ P_{lim}+dpwi &{} \text {Inertia control (activated)} \\ P_{lim}+w_{sho}+dpwi &{} \text {Active Power and inertia controls (activated)} \end{array} \right. \end{aligned}$$

WTG Power versus Wind Speed Curve and the Study Cases: Based on the $v_{wind}$ range, the dynamics of the WTG can be divided into regions. Giving the parameter values in Tables 1 and 2, we have the following cases:

• Region 1: Wind speeds between the minimum cut off speed (3 m/s) and 8.2 m/s. Within this range, the Pitch angle $\theta$ is fixed at zero in order to extract all possible power from the air, as the rated power is not reached by this range of wind speeds. Also, the rated reference speed, 1.2 pu is reached when $v_{wind}=8.2$ m/s so, the reference speed should be seen to gradually increases versus the wind speed. Therefore, in this region of dynamics, Eq. (35) is considered, while Eqs. (33) and (34) are eliminated, and we set $\theta =0$.

  This case can be further modified by taking into account the activated or deactivated optional controls (active Power and inertia controls). Also, it can be modified to any of the reactive power cases.

• Region 2: Wind speeds between 8.2 and 11.4 m/s. In this region, the reference speed is at the rated level 1.2 pu, while the power remains below the rated level. The WTG reaches the rated power 1 pu at $v_{wind}=11.4$ m/s. Therefore, in this region, Eqs. (35), (33), and (34) are eliminated and we set $w_{ref}=1.2$ and $\theta =0$. As in the previous case, this case can be further modified.

• Region 3: Wind speeds between 11.4 and 25 m/s (the maximum allowed speed). The dynamics of this region take into consideration Eqs. (33)–(34), while Eq. 35 is eliminated and we set $w_{ref}=1.2$. Also this case can be further modified as mentioned in the previous cases.

We built a numerical simulator for the dynamical system in the three regions above. The stable steady state of the generated electric power versus wind speeds is as expected for any WTG power curve profile. Figure 13 shows the result of the simulation in the three regions of dynamics, and the power curve profile for the WTG.

Fig. 13

Power curve profile for the WTG

2.3 Documented Results and Conclusions About the Model

In this subsection, we present some of the important information and conclusion that have been made about the model derived in Sect. 2.2.1. These points and conclusions are summarized below:

• Parameters: The model’s parameters can be different based on the sources found in literature. Therefore, scholars are encouraged to determine the conditions in which their model is used. For instance, some few differences can be found between [2, 3, 13, 18, 20]. However, we remark that later in Sect. 3.4 we verified our model versus real data, which suggest credibility for the parameters given in Tables 1 and 2. These parameters are mainly taken from [2, 3] and also some from [18].

• Stability: Stability for the model has been significantly studied through eigenvalues as in [5, 25]. It seems however, from [5] that in the case of the power factor set up (see Sect. 2.2.2), only the grid parameters (R and X) can have a large effect on transitioning the system from Stable to Unstable. Figure 14 shows the region where Stability and Instability occurs in the grid parameter space. We note that Fig. 14 has been produced in [5, 8, 10] respectively for the model in all ranges (Regions 1,2 and 3) of wind speeds introduced in Sect. 2.2.2 and Fig. 13. However, it is important to notice that [5] reported the possibility of a Hopf bifurcation for very small value of X. Note that small values of X has been reported by the NREL [26] to also cause the WTG acting funny and break. The interesting part about small value of X that it can lead to a Hopf bifurcation behavior, but also under the control limits given in Table 3 as discussed in [5]. This phenomenon of how allowable oscillations can be allowed by the WTG controls as reported by the NREL [26], has been further investigated in [12] to continue on the work of [5] and use the model provided in this chapter to provide a theoretical explanation for the phenomenon. On the other hand, if the system is in the supervisory voltage reactive power control set up (see Sect. 2.2.2), then it is required to have the $Q_{droop}$ function “activated” to maintain stability (see [6, 11]). As a matter of fact, the $Q_{droop}$ function has to be in a a feedback mode that is feeding a gain of the reactive power delivered to the grid to have stability, not just a specific constant (see [6, 11]).

• Parameter Sensitivity: Checking how the system steady states and local trajectories would react (change in response) to small changes in a given parameter has been studied in [4, 8,9,10]. In these papers, it was concluded that they system is highly sensitive to $v_{wind}$ and sensitive enough to all grid parameters X, R and E for all wind speed ranges (Regions 1,2 and 3, Fig. 13). To determine local trajectories sensitivity to parameters, we need to study eigenvalue sensitivity to parameters as done in [9]. Only the region (Region 3, Fig. 13) has eigenvalue sensitivity towards $v_{wind}$, which will be included in our study to the Pitch control next section.

• Boundedness, Existence and Uniqueness: If we consider the control limits (bounds) given in Table 3, it can be shown mathematically that the network equation in Eq. (51) has a unique solution that allow us to have the system in differential equations instead of the system being in differential-algebraic equations. As proved and introduced in [7], We can use directly Eq. (52) to represent V:

  $$\begin{aligned} V=f(I_{plv},E_q;X;R;E)=\frac{-B + \sqrt{B^2 - 4AC}}{2A} \end{aligned}$$

  (52)

  With $A=1+\frac{2X}{X_{eq}}+\frac{R^2+X^2}{X_{eq}}$, $B=-\left[ 2I_{plv}R+\frac{2XE_q}{X_{eq}} +\frac{2(R^2+X^2)E_q}{X_{eq}}\right]$ and $C=\frac{R^2+X^2}{X_{eq}}+(R^2+X^2)I^2_{plv}-E^2$. This reduction helps significantly in any nonlinear optimization and/or control study. To the best of our knowledge, no WTG system has been mathematically analyzed to even conclude existence and uniqueness for the resultant system of differential equations, as have been done in [7]. It is also worth mentioning that in [7], it was mathematically proved and found that there is a safe region in the parameter space of R and X, in which the system always maintains existence and uniqueness of solutions. This region is given in the Fig. 15.

• Multiple Time Scale Structure: In [7] and intensively in [8], it has been shown that the WTG system has different time scales in it. In fact, it was shown that the system can reduces into fast-slow (two) time scales or fast-medium-slow (three) time scales. This is the first time in literature, as we think, that some study covered the multiple time structure in WTGs. Reduction to the model (two or three time scales), with guaranteeing eventual convergence (shown in [7, 8]), can expand and enhance the real time domain simulations and provide nonlinear studies with another tool to use while studying the WTGs.

• Eliminating the control limits: In [6, 11], it was shown that the attraction limits in the case of stability are larger than the control limits provided in Table 3. In another words, the stable steady states are shown to attract trajectories in a range that is even larger than the control limits. This, as concluded by [6, 11] means that the limiters can be eliminated when we build simulations for the system, at least if we are concerned about small-signal stability studies. The reader then is recommended to take a look at how the block diagrams, in transfer function, for the WTG components/controls, look like without any of the limiters in [11].

Fig. 14

Stable (red) and Unstable (Black)

Fig. 15

Safe region in which solutions uniquely exists

3 Pitch Control, Simulations, Simulink Verification and Real Data Validation

3.1 Modeling and Analysis of Pitch Control

In this subsection, we provide a full time domain study for the dynamics in Region 3 (see Fig. 13) where the important Pitch control is activated. We start first by considering the power factor setup for the range of wind speeds in Region 3 (11.4–25 m/s) with the two mass model,the power factor, and without the active power and inertia controls. Next subsection, we expand the analysis to the reactive power control being in the set up of supervisory voltage and, having the $Q_{droop}$ function in effect. The differential equations reduce to Eqs. (29)–(34), (36), (38)–(39), (48)–(50). For this system of 12 nonlinear differential equations, there is no algebraic (network) equation, as we eliminate the algebraic equation using Eq. (52). We find the steady states versus the wind speed, so we can see the Pitch control function that stabilizes the system. We study stability in parameter space.

3.1.1 Pitch Control with Power Factor

The Steady States and Eigenvalues: Once the wind speed approaches 11.4 m/s, the power extracted from the air-streams exceeds the 1 pu (rated power). Consequently, the Pitch control gets into action and enforce less power extraction. Figure 17 shows the Pitch angle in steady state as a function of wind speed. Because of the Pitch dynamics, in the steady state $P_{elec}=P_{mech}=P_{inp}=P_{1elec}=1$. Figure 16 shows what happens to the power to be extracted if the Pitch are fixed at zero versus when the Pitch control is activated. Since the Pitch control fix the power generation, the physical steady state in Region 3 is constant versus $v_{wind}$. We computed these values, $w_g=w_t=0.2$, $E_q=E_{qcmd}=1.167$, and $V=V_{ref}=1.039$.

Fig. 16

$P_{mech}$ when the pitch angle is fixed at zero versus the pitch control activated

Fig. 17

Pitch angle steady state as a function of $v_{wind}$

Because the $C_p$ function is forth degree polynomial of $\theta$, the resultant steady states are not necessary unique. We ran tests numerically to see if there are other possible steady states. For every fixed wind speed, we could find two different Pitch angles. One of these steady states is negative and the other is positive. As a result we fixed our codes to only find these Pitch angles that are in the acceptable range. For instance, $v_{wind}=20$ is associated with $\theta = -3.775$ and $\theta = 19.115$ as steady states values. Our code then chooses only $\theta = 19.115$. It is important to hint that only the acceptable range of Pitch angles belong to a locally stable set of steady states. When the Pitch control is deactivated in other Regions, the eigenvalues showed no sensitivity to the wind speed (see Sect. 2.3). In Region 3, the eigenvalues are highly sensitive to $v_{wind}$. Table 4 shows complex pair of the eigenvalues and their change when $v_{wind}=11.4$ m/s and $v_{wind}=25$ m/s. The sixth column presents the percentage of change for both the real part and the imaginary part respectively.

Table 4 The eigenvalues computed at the steady state

Grid Parameters and Stability: The resistance R and the reactance X are the grid parameters of interest (see Fig. 11). Changes in parameter, while fixing $v_{wind}=12$ in our trial, is expected to have an effect on the terminal voltage. We ran a code that discretized the parameter space of R and X using a high resolution unit square grid, and found the steady states based on the given parameters at each point (Fig. 14). The code computes the Jacobian matrix and linearizes around the steady states. The reader is recommended to see [5] for Figures of the steady states plotted in the grid parameter space.

3.2 Pitch Control and Q Droop Function

By setting up the system to be the supervisory voltage case and two-mass rotor model, the model reduces to Eqs. (29)–(35), (39)–(44), and (48)–(50). Note that the model can reduce again depending on the wind speed Region of interest (Regions 1, 2 and 3 in Fig. 13). Equation (40) has the formulation of the Q Droop function dynamics. Furthermore, the effect of this dynamics is in the term $V_{qd}=K_{qd}Q_{droop}$ (Eqs. (42)–(43)), which eventually lead to $Q_{ord}$ in Eq. (40). The Q Droop function is activated when the gain $K_{qd}$ is larger than 0. The Q Droop function is a slow acting function, and is supposed to help reducing the effective reference voltage in the reactive power control, corresponding the changes in the reactive power control. The result of applying this function is to have improved coordination between multiple integral controllers regulating the same point in the system. This positive result is claimed by GE [3]. As described by more details in [6, 11] the system has to have the Q Droop function activated to maintain stability. Moreover, this activation has to be a feedback mode from the reactive power delivered to the grid, that is $V_{qd}=K_{qd}Q_{gen}$ in Eqs. (42)–(43), and not to have $Q_{droop}$=constant, as this has shown to cause instability [5]. This is a very important consideration and result both [6, 11]. It is important to mention that in throughout and detailed analysis [11] has shown that $Q_{droop}$=constant result in an unstable system, which directly contradict the GE claim in [3] that the $Q_{droop}$=constant is acceptable.

In Region 3 ($11.4<V_{wind}<25$), the physical state variables are constant as discussed earlier. As suggested in [3], we have $K_{qd}=0.04$. We fixed $v_{wind}=11.4$ m/s and computed the steady states in Table 5 by varying the gain $K_{td}$ to test its sensitivity. Similarly, Table 6 is for the eigenvalues. It is noticeable that changing $K_{td}$ from 0.04 to 0.06 ($50\%$ change) have the changes $67\%$, $0.3\%$, $8.6\%$, and $1\%$ in $Q_{gen}$, V, $E_q$, and $I_{plv}$ respectively. It can be noted as well that some of the eigenvalues had over a $100\%$ change. In Table 6, the sixth column has the change in percentage (real and imaginary parts respectively). From these results it is clear that the gain parameter $K_{dq}$ has direct effects on both the steady states and the eigenvalues. Eigenvalues sensitivity means that this parameter can affect local trajectories behavior, so it is important to have more parameter estimate studies, especially if tunning is needed based on the application conditions.

Table 5 Steady sates versus $K_{td}$

Table 6 Eigenvalues at $v_{wind}=11.4$

3.3 Simulations

3.3.1 System Response to a Pulse Wind Profile

Figure 18 shows a $v_{wind}$ profile for a pulse changing from 20 to 21 m/s and again to 20 m/s with the system response. The profile equation is $v_{wind} = 20+e^{-(t-10)^2}$.

Fig. 18

System response for a given wind profile (upper graph)

3.3.2 System Response to a Drop-Clear in Terminal Voltage

Figure 19 shows a drop-clear in terminal voltage and the system’s response.

Fig. 19

Drop-clear in the terminal voltage (upper graph) along with the system’s response

3.3.3 System Response to a Droop-Clear in the Reactance X

Figure 20 shows a droop-clear case of the reactance X. The dropping happens from a stable condition to an unstable one, passing a Hopf bifurcation, as discussed in Sect. 2.3), and then returning to the stable status. The system is capable of stabilizing after clearing the severe disturbance as shown in the simulation.

Fig. 20

Droop-clear in the reactance X (upper graph) and the system’s response

3.3.4 Basin of Attraction Versus Control Limits

Testing the Attraction Limits Versus Control Limits: As found by strong and detailed study/simulation in [11], the region of attraction around the steady states seems to be larger than the control limits themselves. Let us consider x and $x_0$ be the vectors of the steady states and initial conditions respectively. Figure 21 represents a simulation for the dynamics having initial condition $x_0 = x+0.5\left| x \right|$. The simulation had fixed wind speed. Notice that initial values and the trajectories exceeded the limiters (control limits) in solid black lines and are still attracted to the stable steady state eventually.

Fig. 21

State trajectories (blue) and limiters (black)

Testing the Derivatives of some Mechanical State Variables in Extreme Cases: Since on of the main things of interest for the system is how it responds to sudden disturbances, we tested the system response and both $\frac{dP_{inp}}{dt}$ and $\frac{d\theta }{dt}$ for a sudden but continuous wind disturbance and terminal voltage drop. Figure 22 shows some of the state variables’ response to the given wind profile. The derivatives of the power order and the Pitch angle do not exceed their control limits. Figure 23 has the same trajectories response but for a sudden drop in the terminal voltage. Note that one of the states exceeded the control limits. The conducted simulations indicate that the trajectories response and the mechanical derivatives limits respond within the control limits for very disturbing pulse of wind.

Fig. 22

State trajectories (blue) and limiters (black)

Fig. 23

State trajectories (blue) and limiters (black)

3.3.5 Effect of the Q Droop Function

We tested the system by by running a simulation, with and without $Q_{droop}$ function, for a pulse wind speed profile. This should help us emphasize how the integrator variables $Q_{wvl}$ and $Q_{wvu}$ will behave. For the wind profile in Fig. 24, the integrators seem unable to stabilize after the pulse effect. While, In real life the limiters will intervene to prevent such divergences, the same pulse effect could not force the integrators to diverge when the $Q_{droop}$ function is used. This indicates that the Q Droop helps stabilizing the system in extreme cases through improving the performance of the integrator.

Fig. 24

Trajectories response with (blue) and without (red) $Q_{droop}$

3.4 Verification and Validation of the Model

3.4.1 Simulink Verification

Simulink projects were built for the transfer functions of the model given by GE [2, 3] and NREL [13]. The purpose is to verify that our differential equations model (Eqs. (29)–(50)) is typical in results when compared to the Simulink simulations. For more information about the verification, the reader is recommended to refer [8]. First project constructed a Simulink project of the system in Fig. 27 and ran the numerical solver ODE15s in Matlab for a fixed wind speed of $v_{wind}=8.2$ m/s, which makes the model in Region 2 (see Sect. 2.2.2 and Fig. 13). The results of the simulation are typical. Figure 25 represents one of the results for V (the initial condition is the same in both Simulink and ODE15s). The similarity of the results of V is very important as it is the main term to calculate both the active and reactive power. Second project constructed a Simulink project (Fig. 28) with an oscillating wind speed ($v_{wind}=8+\sin (10t)$). The dynamics in this case is in Region 1, see Sect. 2.2.2 and Fig. 13. The result was also typical. Figure 26 presents $P_{elec}$ response to the continuous oscillation of $v_{wind}$.

Fig. 25

Response of implementations in Matlab (differential equations) and Simulink to zero initial conditions

Fig. 26

$P_{elec}$ in the steady response from the model and Simulink

Fig. 27

Simulink project for a fixed wind speed

Fig. 28

Simulink project for an oscillating wind speed

3.4.2 Validation Versus Real Measured Data

In this validation we re-used what we provided in [8, 11]. The models chosen for comparison are [18, 20] as they are a highly cited academic source that also are inclusive in their modeling. We focus on one of the clear differences between our model and theirs. Both the generator and turbine speeds are controlled by the reference speed $w_{ref}$ (see Rotor Model discussion in Sect. 2.1). The rated reference speed is 1.2 pu, however, for lower wind speeds, this is not physically possible. Therefore, the reference speed changes slowly with $P_{elec}$ until it reaches 1.2 pu (see Fig. 10). Our model and the models [18, 20] have different curves for lower wind speeds $w_{ref}=-0.67P_{elec}^2+1.42P+0.51$ in our model and $w_{ref}=-0.75P_{elec}^2+1.59P+0.63$ in their models (Fig. 29). Figure 10 shows different $w_{ref}$ curves. To test the effects of this difference between our model and the models considered in the comparison, we generated the power-wind speed profile for all the models (stable steady state of $P_{elec}$ vs. $v_{wind}$) and plotted them with real measured data (re-use of the same data in [8, 11]). Figure 30 illustrates this comparison and validation with real measure data.

Fig. 29

$w_{ref}$ from our model in solid with [18, 20] doted, and the rated speed dashed

Fig. 30

Real data of a WTG (stars) versus power-wind speed curves for our model in solid and the models [18, 20] dashed. The Fig. is re-used from [8, 11]

Observations from the comparison and the validation:

• 1. As seen in Fig. 10 when comparing our model versus [18, 20], we see that $w_{ref}$ reaches the rated value (1.2 pu) at $P_{elec}\approx 0.45$ pu in our model, while it reaches the rated value (1.2 pu) at $P_{elec}\approx 0.75$ pu in their model. The manufacturer (see page 35, [3]) recorded that $w_{ref}$ only has to follow some feed back from $P_{elec}$ below $P_{elec}=0.46$ pu, as this is the stage where the system can start having $w_{ref}=1.2$. This indicates that our model is more practical and matches the specifications recorded by the manufacturer.

• 2. Our model has relatively better power-wind speed profile when compared to [18, 20] and the real time measured data (Fig. 30). The stable steady state of $P_{elec}$ is not an average for the measured data. However, when the size of the measured data is very large, which is the case in our trial, the data may be expected to have some form of normal distribution around the stable steady state. Our model shows better results if we have this explanation in consideration.

• 3. The power-wind speed profile in Fig. 30 can be generated with either the reactive power control in power factor or supervisory voltage mode (see Fig. 4). The supervisory voltage mode is preferable as it is associated with having the WTG as a member in a group of WTGs as opposed to have the WTG as a separate unit (power factor mode). We remark that stability of $P_{elec}$ and the whole system is not possible without having the Q Droop function in effect (explained in Sect. 3.2). There is almost no explanation about how to implement Q Droop function and/or analyzing its effect and possible cases in other models throughout our search to date in the literature and cited papers that are considered major sources of modeling for WTGs.

4 Conclusion

In this chapter, a state-of-the-art modeling effort, that represents the WTG dynamics and control, is provided. This modeling efforts summarize and collect very recent publications and is validated and verified versus real measured data and Simulink simulations. An advantage from the collective modeling presentation in this chapter, is that one can use numerical solvers such as ODE15s to simulate the WTG system for different scenarios and conditions, without the need for commercial and special simulators. The pitch control, that is essential for the WTG system to keep the power production stable and saturated at the rated requirement, is discussed and analyzed by detail in this chapter. Moreover, the chapter provides the reader with all important technical information regarding this important control as is in industry, such as: stability, sensitivity, resilience in different reactive power modes and a lot of demonstrative simulations.

Copyright

The author has obtained permission from GE publisher for reusing Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10 and 12. The other Figs are either new or re-generated/re-used by the author himself from earlier work (properly cited).