Keywords

1 Introduction

There has been increasing demand for the exploration of the sea along the coastal areas for land and energy. The construction of VLFS has been advantageous as compared to traditional sea reclamation and bottom supported offshore structures. These structures are huge in length as compared with the wavelength of the ocean waves, and hence wave-induced rigid body motions are negligible. These structures are considered to be flexible, and hence the study of hydroelastic behaviour becomes more important than their rigid body motions. These structures are usually constructed near shore, and hence the effect of sea bottom profile becomes significant. The sea bottom is not flat throughout; there are various kinds of undulation which give rise to wave refraction, shoaling and wave breaking. Most of the studies performed by researchers have considered the structure to be thin for the hydroelastic analysis of VLFS based on Euler–Bernoulli beam theory but these structures have an accountable thickness, and hence Timoshenko–Mindlin’s plate theory is more realistic for the analysis as formulated by Mindlin [16].

A significant study using the Timoshenko–Mindlin’s thick plate theory was carried out by researchers [2, 9, 11, 17] for wave interaction with sea ice and wave interaction with offshore floating structure. The scattering of waves for varying water depth was analysed by Evans and Linton [8] transforming the problem into a uniform strip resulting in a variable free-surface boundary condition. Athanassoulis and Belibassakis [1] derived a consistent coupled-mode theory for the propagation of small amplitude water waves over variable bathymetry regions. Kyoung et al. [15] considered an influence of sea bottom topography on the hydroelastic response of a very large floating structure (VLFS). The finite element method based on the variational formulation is used to calculate the sea bottom effects in the fluid domain. Karmakar and Sahoo [12] analysed the scattering of surface water waves by a semi-infinite floating membrane due to an abrupt change in bottom topography. Further, Karmakar et al. [13] studied the oblique flexural gravity-wave scattering by multiple step bottom topography in finite water depth and shallow water approximations. The energy relation is derived for the oblique flexural gravity-wave scattering due to a change in bottom topography using the argument of wave energy flux. Bhattacharjee and Soares [5] investigated diffraction of obliquely incident waves by a floating structure near a wall with step-type bottom topography in finite water depth and shallow water approximations. Eigenfunction expansion method was used to obtain the solution of the problem under the potential flow approach. Karmakar and Soares [14] performed the study on the interaction of oblique incident wave with a moored floating membrane for both the cases of finite water depth and shallow water approximation with changes in bottom topography. The energy relation was also derived for the oblique gravity wave in the presence of floating membrane due to an abrupt change in bottom topography for various cases using the law of conservation of energy flux and alternately by the direct application of Green’s second identity.

The studies on the wave interaction with floating structures with change in bathymetry were performed by researchers to analyse the effect of bottom topography in the wave transformation. Belibassakis and Athanassoulis [3, 4] and Belibassakis et al. [6] extended the coupled-mode model applied to the hydroelastic analysis of three-dimensional large floating bodies of shallow draft or ice sheets of small thickness, lying over variable bathymetry regions. The hydroelastic mode series expansion of the wave field is adopted, enhanced by an appropriate sloping bottom mode to treat the wave field beneath the elastic floating plate, down to the sloping bottom boundary. Rezanejad et al. [18] analysed the effect on the efficiency by implementing a dual-chamber oscillating water column (OWC) placed over the stepped bottom. Matched eigenfunction expansion and boundary integral equation method (BIEM) was used to analyse the change in the topography on the power generation. Choudhary and Martha [7] examined the diffraction of surface water waves by an undulating bed in the presence of different kinds of thin vertical barriers. Gerostathis et al. [10] extended the coupled-mode model applied to the hydroelastic analysis of three-dimensional large floating bodies of shallow draft lying over variable bathymetry regions. A general bathymetry is assumed, characterised by a continuous depth function joining two regions of different depths.

In the present study, the wave scattering by a floating elastic plate is analysed based on Timoshenko–Mindlin’s thick plate theory in finite water depth with varying bottom topography. The eigenfunction expansion method with mode-coupling relation is applied to obtain the solution for the case of wave interaction with freely floating articulated elastic plate. The free-free edge of the floating elastic plate is considered in the analysis. The bottom topography is considered to be stepped type topography and the effect of stepped bottom topography is analysed by varying the water depth in wave transmitted region. The numerical computation is performed to analyse the wave reflection, wave transmission and hydroelastic behaviour of an elastic plate under the action of the incident wave with varying bottom topography.

2 Mathematical Formulation

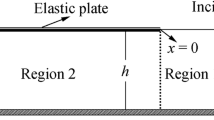
The scattering of waves due to finite floating elastic plate based on Timoshenko–Mindlin’s thick plate theory with changing bottom topography is analysed under the assumption of linearised wave theory. The monochromatic wave is incident on the thick floating elastic plate along the positive x-direction. A two-dimensional coordinate system is considered in the analysis with x-axis being the horizontal and the y-axis considered vertically downward positive as shown in Fig. 1. The fluid domain in finite water depth is divided into three regions, upstream open water region at \( 0 < x < \infty , 0 < y < h_{1} \) as region 1, the finite thick floating elastic plate covering the free surface of the fluid at \( - a < x < 0, 0 < y < h_{2} \) as region 2 and downstream open water domain at \( - \infty < x < - a, 0 < y < h_{3} \) as region 3. The two edges of the plate at \( x = 0 \) and \( x = - a \) are considered to satisfy free-free edge boundary condition. The floating elastic plate is considered to be having considerable thickness and modelled under the assumption of Timoshenko–Mindlin plate theory.

Fig. 1
figure 1

Schematic diagram for thick floating elastic plate in changing bottom topography

Full size image

Under the assumption of linearized wave theory, the velocity potential, \( \Phi_{j} (x,y) \) for \( j = 1,2,3 \) satisfies the Laplace’s equation given by

$$ \nabla^{2}\Phi_{j} \left( {x,y} \right) = 0\, {\text{at}}\, - \infty < x < \infty ,0 < y < h_{j} , \quad j = 1,2,3. $$
(1)

The linearised kinematic boundary condition at the mean free surface is of the form

$$ \zeta_{jt} =\Phi_{jy} ,\,{\text{at}}\quad y = 0. $$
(2a)

The dynamic free-surface boundary condition is given by

$$ \rho\Phi_{jt} - \rho g\zeta_{j} = p_{\text{atm}} \quad {\text{at}} \quad y = 0, $$
(2b)

where \( p_{\text{atm}} \) is the atmospheric pressure. The bottom boundary condition is given by

$$ \Phi_{jy} = 0,\, {\text{at}}\, y = h_{j} ,\quad j = 1,2,3. $$
(3)

In the plate-covered region, it is assumed that the plate satisfies the Timoshenko–Mindlin’s equation [9] which includes the effect of rotary inertia and transverse shear deformation is of the form

$$ \left( {\partial_{x}^{2} - \frac{{\rho_{p} }}{\mu Gd}\partial_{t}^{2} } \right)\left( {EI\partial_{x}^{2} - \frac{{\rho_{p} d^{3} }}{12}\partial_{t}^{2} } \right)\zeta_{2} + \rho_{p} d\partial_{t}^{2} \zeta_{2} = - \left( {1 - \frac{EI}{\mu Gd}\partial_{x}^{2} + \frac{{\rho_{p} d^{2} }}{12\mu G}\partial_{t}^{2} } \right)p. $$
(4)

where d is the plate thickness, \( \rho_{p} \) is the plate density, \( EI = {{Ed^{3} } \mathord{\left/ {\vphantom {{Ed^{3} } {12(1 - \nu^{2} )}}} \right. \kern-0pt} {12(1 - \nu^{2} )}} \) is the plate rigidity, E is the Young’s modulus, \( \nu \) is the Poisson’s ratio, \( G = {E \mathord{\left/ {\vphantom {E {2\left( {1 + \mu } \right)}}} \right. \kern-0pt} {2\left( {1 + \mu } \right)}} \) is the shear modulus of the plate, p is the pressure and \( \mu \) is the transverse shear coefficient of the plate. Assuming that the wave elevation and the plate deflection are simple harmonic motion in time with frequency \( \omega \), the velocity potential \( \Phi_{j} \left( {x,y,t} \right) \) and the surface deflection \( \zeta_{j} \left( {x,t} \right) \) can be written as \( \Phi_{j} \left( {x,y,t} \right) = {\text{Re}}\left\{ {\phi_{j} \left( {x,y} \right)} \right\}e^{ - i\omega t} \) and \( \zeta_{j} \left( {x,t} \right) = {\text{Re}}\left\{ {\eta_{j} \left( x \right)} \right\}e^{ - i\omega t} \), where \( {\text{Re}} \) denotes the real part. In the open water region \( j = 1,3 \), the linearized free-surface boundary condition is given by

$$ \partial_{y} \phi_{j} - \left( {\frac{{\omega^{2} }}{g}} \right)\phi_{j} = 0,\quad {\text{for}}\;x < - a\,{\text{and}}\,x > 0, $$
(5)

The plate-covered boundary condition is obtained by combining the linearised kinematic condition at the surface and Timoshenko–Mindlin’s equation as

$$ \begin{aligned} & \left\{ {\frac{EI}{{\left( {\rho g - m_{s} \omega^{2} } \right)}}\partial_{x}^{4} + \left( {\frac{{m_{s} \omega^{2} I}}{{\left( {\rho g - m_{s} \omega^{2} } \right)}} - S} \right)\partial_{x}^{2} + \left( {1 - \frac{{m_{s} \omega^{2} IS}}{EI}} \right)} \right\}\phi_{2y} \\ & \quad + \frac{{\rho \omega^{2} }}{{\left( {\rho g - m_{s} \omega^{2} } \right)}}\left\{ {1 - \frac{{m_{s} \omega^{2} IS}}{EI} - S\partial_{x}^{2} } \right\}\phi_{2} = 0,\quad {\text{for }} - a < x < 0, \\ \end{aligned} $$
(6)

where \( \rho \) is the density of water, \( m_{s} \) is the mass of the plate, \( I = {{d^{2} } \mathord{\left/ {\vphantom {{d^{2} } {12}}} \right. \kern-0pt} {12}} \) is the rotary inertia and \( S = EI/\mu Gd \) is the shear deformation for the Timoshenko–Mindlin’s equation. The continuity of velocity and pressure at the interface \( x = - a \) and \( x = 0 \), \( 0 < y < h_{j} \), \( j = 1,2 \) is given by

$$ \phi_{jx} = \phi_{{\left( {j + 1} \right)x}} \,{\text{and}}\,\phi_{j} = \phi_{{\left( {j + 1} \right)}} \quad {\text{at}}\quad x = - a\,{\text{and}}\,x = 0, 0 < y < h_{j} . $$
(7)

The floating elastic plate is considered to be freely floating, so the bending moment and the shear force at the edges \( x = - a \) and \( x = 0 \), \( 0 < y < h_{2} \) satisfies the relation

$$ \partial_{y}^{3} \phi_{2} \left( {x,y} \right) = 0{\text{ and }}\partial_{{xy^{3} }}^{4} \phi_{2} \left( {x,y} \right) = \wp \partial_{xy}^{2} \phi_{2} \left( {x,y} \right){\text{ for }}x = - a{\text{ and }}x = 0{\text{ at }}y = 0, $$
(8)

with \( \wp = \left\{ {\frac{{\,m\omega^{2} (S + I)}}{EI}} \right\} \). The far-field radiation condition is given by

$$ \phi_{j} \left( x \right) = \left\{ {\begin{array}{*{20}l} {\left( {e^{{ - ik_{10} x}} + R_{0} e^{{ik_{10} x}} } \right)f_{10} \left( y \right)} \hfill & {{\text{as}}\;x \to \infty ,} \hfill \\ {\left( {T_{0} e^{{ - ik_{30} x}} } \right)f_{30} \left( y \right)} \hfill & {{\text{as}}\;x \to - \infty ,} \hfill \\ \end{array} } \right. $$
(9)

with \( R_{0} \) and \( T_{0} \) are the complex amplitudes of the reflected and transmitted waves and \( k_{j0} \) for \( j = 1,3 \) are the positive real roots that satisfy the dispersion relation given by

$$ k_{j0} \tanh k_{j0} h_{j} - {{\omega^{2} } \mathord{\left/ {\vphantom {{\omega^{2} } g}} \right. \kern-0pt} g} = 0. $$
(10)

In the next section, the solution procedure of the wave interaction with finite floating elastic plate with changing bottom topography is presented and discussed in detail.

3 Method of Solution

In this section, the scattering of waves due to the finite floating elastic plate over varying bottom topography is analysed based on Timoshenko–Mindlin plate theory.

The boundary value problem for the scattering of wave by a finite floating elastic plate over varying bottom topography with free-free edge condition is formulated. The velocity potentials \( \phi_{j} \left( {x,y} \right) \) for \( j = 1,2,3 \) satisfy the governing Eq. (1) along with the boundary condition (3), (5), (6) and (9) as defined in Sect. 2. The velocity potentials \( \phi_{j} \left( {x,y} \right) \) for \( j = 1,2,3 \) at the free surface and the plate-covered regions are of the form

$$ \begin{array}{*{20}l} {\phi_{1} \left( {x,y} \right) = \left( {I_{0} e^{{ - ik_{10} x}} + R_{0} e^{{ik_{10} x}} } \right)f_{10} \left( y \right) + \sum\limits_{n = 1}^{\infty } {R_{n} e^{{ - \kappa_{1n} x}} } f_{1n} \left( y \right)} \hfill & {{\text{for}}\;x > 0,0 < y < h_{1} } \hfill \\ {\phi_{2} \left( {x,y} \right) = \left\{ \begin{aligned} & \sum\limits_{n = 0,I}^{II} {\left( {A_{n} e^{{ - ik_{2n} x}} + B_{n} e^{{ik_{2n} x}} } \right)} f_{2n} \left( y \right) \\ & \quad + \sum\limits_{n = 1}^{\infty } {\left( {A_{n} e^{{\kappa_{2n} x}} + B_{n} e^{{ - \kappa_{2n} x}} } \right)} f_{2n} \left( y \right) \\ \end{aligned} \right\}} \hfill & {{\text{for}}\; - a < x < 0,0 < y < h_{2} } \hfill \\ {\phi_{3} \left( {x,y} \right) = T_{0} e^{{ - ik_{30} x}} \, f_{30} \left( y \right) + \sum\limits_{n = 1}^{\infty } {T_{n} e^{{\kappa_{3n} x}} } f_{3n} \left( y \right)} \hfill & {{\text{for}}\;x < - a,0 < y < h_{3} } \hfill \\ \end{array} $$
(11)

where \( R_{n} ,n = 0,1,2 \ldots ,A_{n} ,B_{n} ,n = 0,I,II,1,2 \ldots \) and \( T_{n} ,n = 0,1,2 \ldots \) are the unknown constants to be determined. The eigenfunctions \( f_{jn} \left( y \right) \)’s are given by

$$ f_{jn} \left( y \right) = \frac{{\cosh k_{jn} \left( {h_{j} - y} \right)}}{{\cosh k_{jn} h_{j} }}\quad {\text{for}}\,n = 0,I,II\quad {\text{and}}\quad f_{jn} \left( y \right) = \frac{{\cos k_{jn} \left( {h_{j} - y} \right)}}{{\cos k_{jn} h_{j} }}\quad {\text{for}}\,n = 1,2,.. $$
(12)

where \( k_{jn} \;{\text{for}}\;j = 1,3\;{\text{and}}\;n = 0 \) are the eigenvalues. These eigenvalues satisfy the dispersion relation in the open water region given by

$$ k_{j0}^{{}} \tanh k_{j0}^{{}} h_{j} - {{\omega^{2} } \mathord{\left/ {\vphantom {{\omega^{2} } g}} \right. \kern-0pt} g} = 0. $$
(13)

with \( k_{jn} = i\kappa_{jn} \,{\text{ for}}\, n = 1,2 \ldots \) and the dispersion relation has one real root \( k_{j0} \) and an infinite number of purely imaginary roots \( \kappa_{jn} \,{\text{ for}}\, n = 1,2 \ldots \) In the plate-covered region, the \( k_{jn} \,{\text{ for}}\, j = 2 \) satisfies the dispersion relation given by

$$ \left( {\alpha_{0} - \alpha_{1} k_{jn}^{2} + \alpha_{2} k_{jn}^{4} } \right)k_{jn} \tanh k_{jn} h_{j} - \left( {\beta_{0} - \beta_{1} k_{jn}^{2} } \right) = 0. $$
(14)

where \( \alpha_{0} = \left\{ {1 - m_{s} \omega^{2} \left( {\frac{IS}{EI}} \right)} \right\} \), \( \alpha_{1} = \left\{ {\frac{{m_{s} \omega^{2} I}}{{\left( {\rho g - m_{s} \omega^{2} } \right)}} - S} \right\} \), \( \alpha_{2} = \frac{EI}{{\left( {\rho g - m_{s} \omega^{2} } \right)}} \), \( \beta_{0} = \frac{{\rho \omega^{2} }}{{\left( {\rho g - m_{s} \omega^{2} } \right)}}\left( {1 - m_{s} \omega^{2} \frac{IS}{EI}} \right) \), \( \beta_{1} = - \frac{{\rho \omega^{2} S}}{{\left( {\rho g - m_{s} \omega^{2} } \right)}} \), \( I = d^{2} /12 \) is the rotary inertia. The dispersion relation as in Eq. (14) has one real root \( k_{j0} \) and four complex roots \( k_{jn} \,{\text{ for }}\,n = I,II,III,IV \) of the form \( \pm \alpha \pm i\beta \). In addition, there are an infinite numbers of purely imaginary roots \( \kappa_{jn} \,{\text{ for}}\, n = 1,2 \ldots \)

It may be noted that the eigenfunctions \( f_{jn} \left( y \right) \)’s in the open water and plate-covered region satisfy the orthogonality relation as given by

$$ \left\langle {f_{jm} ,f_{jn} } \right\rangle_{j = 1,3} = \begin{array}{*{20}l} 0 \hfill & {{\text{for}}\;m \ne n,} \hfill \\ {C^{\prime}_{n} } \hfill & {{\text{for}}\;m = n,} \hfill \\ \end{array} \quad {\text{and}}\quad \left\langle {f_{jm} ,f_{jn} } \right\rangle_{j = 2} = \left\{ {\begin{array}{*{20}l} 0 \hfill & {{\text{for}}\;m \ne n,} \hfill \\ {C^{\prime\prime}} \hfill & {{\text{for}}\;m = n,} \hfill \\ \end{array} } \right. $$
(15)

with respect to the orthogonal mode-coupling relation defined by

$$ \left\langle {f_{jm} ,f_{jn} } \right\rangle_{j = 1,3} = \int\limits_{0}^{{h_{j} }} {f_{jm} (y)f_{jn} } (y)dy, $$
(16a)
$$ \begin{aligned} \left\langle {f_{2m} ,f_{2n} } \right\rangle & = \int\limits_{0}^{{h_{j} }} {f_{2m} (y)f_{2n} } (y)dy - \frac{{\alpha_{1} }}{{Q\left( {k_{2n} } \right)}}\left\{ {f^{\prime}_{2m} (0)f^{\prime}_{2n} (0)} \right\} \\ & \quad + \, \frac{{\alpha_{2} }}{{Q\left( {k_{2n} } \right)}}\left\{ {f^{\prime\prime\prime}_{2m} (0)f^{\prime}_{2n} (0) + f^{\prime}_{2m} (0)f^{\prime\prime\prime}_{2n} (0)} \right\} + \frac{{\beta_{1} }}{{P\left( {k_{2n} } \right)}}f_{2m} (0)f_{2n} (0), \\ \end{aligned} $$
(16b)

where \( C^{\prime}_{n} = \frac{{2k_{jn} h_{j} + \sinh 2k_{jn} h_{j} }}{{4k_{jn} \cosh^{2} k_{jn} h_{j} }},j = 1,3. \)

$$ C^{\prime\prime}_{n} = \frac{{(\alpha_{0} - \alpha_{1} k_{jn}^{2} + \alpha_{2} k_{jn}^{4} )2k_{jn} h_{j} + (\alpha_{0} - 3\alpha_{1} k_{jn}^{2} + 5\alpha_{2} k_{jn}^{4} )\sinh 2k_{jn} h_{j} + (4\beta_{1} k_{jn} \cosh^{2} k_{jn} h_{j} )}}{{(4k_{jn} \cosh^{2} k_{jn} h_{j} )(\alpha_{0} - \alpha_{1} k_{jn}^{2} + \alpha_{2} k_{jn}^{4} )}}. $$

\( P\left( {k_{2n} } \right) = \left( {\alpha_{0} - \alpha_{1} k_{2n}^{2} + \alpha_{2} k_{2n}^{4} } \right) \) and \( Q\left( {k_{2n} } \right) = \left( {\beta_{0} - \beta_{1} k_{2n}^{2} } \right) \).

The constant term \( C^{\prime}_{n} \), \( C^{\prime\prime}_{n} \), \( P\left( {k_{2n} } \right) \) and \( Q\left( {k_{2n} } \right) \) for \( n = 1,2, \ldots \) are obtained by substituting \( k_{jn} = i\kappa_{jn} \,{\text{ for}}\, j = 1,2,3 \).

In order to determine the unknown coefficients, the mode-coupling relation (16b) is applied on the velocity potentials \( \phi_{2} \left( {0,y} \right){\text{ and }}\phi_{2} \left( { - a,y} \right) \) with the eigenfunction \( f_{2m} (y) \). Using the orthogonal property of the eigenfunction \( f_{2m} (y) \) as in Eq. (15) and the expressions of velocity potentials as in Eq. (11) along with the continuity of pressure as in Eq. (7) across the vertical interface \( x = 0, - a, 0 < y < h_{2} \) and also applying the edge condition as in Eq. (8) yields

$$ \begin{aligned} & R_{0} \int\limits_{0}^{{h_{j} }} {f_{10} (y)f_{2m} (y)} dy + \sum\limits_{n = 1}^{N + 2} {R_{n} \int\limits_{0}^{{h_{j} }} {f_{1n} (y)f_{2m} (y)} dy} \\ & \quad + \, \left\{ {\sum\limits_{n = 0,I}^{II} {(A_{n} + B_{n} ) + \sum\limits_{n = 1}^{N} {(A_{n} + B_{n} )} } } \right\}\left[ {\frac{{\alpha_{2} }}{{Q\left( {k_{2n} } \right)}}f_{2n}^{\prime} (0)f_{2m}^{\,\prime \prime \prime} (0) - \frac{{\alpha_{1} }}{{Q\left( {k_{2n} } \right)}}f_{2n}^{\prime} (0)f_{2m\,}^{\prime} (0)} \right. \\ & \quad \left. { + \frac{{\beta_{1} }}{{P\left( {k_{2n} } \right)}}f_{2n} (0)f_{2m} (0) - \delta_{mn} \left\langle {f_{2n\,} ,f_{2m\,} } \right\rangle } \right] = - I_{0} \int\limits_{0}^{{h_{j} }} {f_{10} (y)f_{2m} (y)} \,dy. \\ \end{aligned} $$
(17)
$$ \begin{aligned} & T_{0} e^{{ik_{30} a}} \int\limits_{0}^{{h_{j} }} {f_{10} (y)f_{2m} (y)} dy + \sum\limits_{n = 1}^{N + 2} {T_{n} e^{{ - \kappa_{3n} a}} \int\limits_{0}^{{h_{j} }} {f_{1n} (y)f_{2m} (y)} dy} + \sum\limits_{n = 0,I,II}^{N} {\left( {A_{n} e^{{ - ik_{2n} a}} + B_{n} e^{{ik_{2n} a}} } \right)} \\ & \quad \left[ {\frac{{\alpha_{2} }}{{Q\left( {k_{2n} } \right)}}f_{2n}^{\prime} (0)f_{2m}^{\, \prime \prime \prime} (0) - \frac{{\alpha_{1} }}{{Q\left( {k_{2n} } \right)}}f_{2n}^{\prime} (0)f_{2m\,}^{\prime} (0) + \frac{{\beta_{1} }}{{P\left( {k_{2n} } \right)}}f_{2n} (0)f_{2m} (0) - \delta_{mn} \left\langle {f_{2n\,} ,f_{2m\,} } \right\rangle } \right] = 0. \\ \end{aligned} $$
(18)

where \( k_{jm} = i\kappa_{jm} \,{\text{ for}}\, m = 1,2, \ldots \) and \( \delta_{mn} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{for}}\,m = n,} \hfill \\ 0 \hfill & {{\text{for}}\,m \ne n.} \hfill \\ \end{array} } \right. \)

Again, applying the mode-coupling relation (16b) on \( \phi_{2x} \left( {0,y} \right) \) and \( \phi_{2x} \left( { - a,y} \right) \) with the eigenfunction \( f_{2m} \left( y \right) \) and using the orthogonal property of the eigenfunction \( f_{2m} (y) \) as in Eq. (15) and the expressions of velocity potentials as in Eq. (11) along with continuity of velocity across the vertical interface \( x = 0, - a, 0 < y < h_{2} \) as in Eq. (7) and the edge condition as in Eq. (8) yields

$$ \begin{aligned} & ik_{10} R_{0} \int\limits_{0}^{{h_{j} }} {f_{10} (y)f_{2m} (y)} dy - \,\kappa_{1n} \sum\limits_{n = 1}^{N + 2} {R_{n} \int\limits_{0}^{{h_{j} }} {f_{1n} (y)f_{2m} (y)} dy} \\ & \quad + \, \left\{ {ik_{2n} \sum\limits_{n = 0,I}^{II} {(A_{n} - B_{n} ) - \kappa_{2n} \sum\limits_{n = 1}^{N} {(A_{n} - B_{n} )} } } \right\} \\ & \quad \left[ {\frac{{\alpha_{2} }}{{Q\left( {k_{2n} } \right)}}\left\{ {\wp f_{2n}^{\prime} (0)f_{2m}^{\, \prime} (0) + f_{2n}^{\prime} (0)f_{2m}^{\, \prime \prime \prime} (0)} \right\} - \frac{{\alpha_{1} }}{{Q\left( {k_{2n} } \right)}}f_{2n}^{\prime} (0)f_{2m\,}^{\prime} (0)} \right. \\ & \quad \left. { + \frac{{\beta_{1} }}{{P\left( {k_{2n} } \right)}}f_{2n} (0)f_{2m} (0) - \delta_{mn} \left\langle {f_{2n\,} ,f_{2m\,} } \right\rangle } \right] = - ik_{10} I_{0} \int\limits_{0}^{{h_{i} }} {f_{10} (y)f_{2m} (y)} \,dy. \\ \end{aligned} $$
(19)
$$ \begin{aligned} & - ik_{30} T_{0} e^{{ik_{30} a}} \int\limits_{0}^{{h_{j} }} {f_{30} (y)f_{2m} (y)} dy + \,\kappa_{3n} \sum\limits_{n = 1}^{N + 2} {T_{n} e^{{ - \kappa_{3n} a}} \int\limits_{0}^{{h_{t} }} {f_{3n} (y)f_{2m} (y)} dy} \\ & \quad +\, \left\{ {ik_{2n} \sum\limits_{n = 0,I}^{II} {(A_{n} e^{{ - ik_{2n} a}} - B_{n} e^{{ik_{2n} a}} )} } - \kappa_{2n} {\sum\limits_{n = 1}^{N} {(A_{n} e^{{\kappa_{2n} a}} - B_{n} e^{{ - \kappa_{2n} a}} )} } \right\} \\ & \quad \times \, \left[ {\frac{{\alpha_{2} }}{{Q\left( {k_{2n} } \right)}}\left\{ {\wp f_{2n}^{\prime} (0)f_{2m}^{\, \prime} (0) + f_{2n}^{\prime} (0)f_{2m}^{\, \prime \prime \prime} (0)} \right\}} \right. \\ & \quad \left. { - \frac{{\alpha_{1} }}{{Q\left( {k_{2n} } \right)}}f_{2n}^{\prime} (0)f_{2m\,}^{\prime} (0) + \frac{{\beta_{1} }}{{P\left( {k_{2n} } \right)}}f_{2n} (0)f_{2m} (0) - \delta_{mn} \left\langle {f_{2n\,} ,f_{2m\,} } \right\rangle } \right] = 0. \\ \end{aligned} $$
(20)

for \( k_{jm} = i\kappa_{jm} \,{\text{ for}}\, m = 1,2, \ldots \)

The infinite series sums of the algebraic equations as in (17), (18), (19) and (20) are obtained and the linear equations are truncated up to a finite number of \( N \) terms in order to solve the system of \( \left( {4N + 12} \right) \) equations. The expansion formulae for each of the three regions as in Eq. (11) consists of \( \left( {4N + 12} \right) \) unknown coefficients such as \( R_{n} ,T_{n} \), \( n = 0,1,2, \ldots N,N + 1,N + 2 \), \( A_{n} ,B_{n} ,n = 0,I,II,1,2, \ldots ,N \). On solving the system of algebraic equation, the full solution is obtained in terms of the potential functions with the reflection and transmission coefficients is given by

$$ K_{r} = \left| {R_{0} } \right| \, {\text{and}}\,K_{r} = \left| {\frac{{k_{30} \tanh k_{30} h_{3} }}{{k_{10} \tanh k_{10} h_{1} }}T_{0} } \right|. $$
(21)

The reflection and transmission coefficients are observed to satisfy the energy balance relation \( K_{r}^{2} + \chi K_{t}^{2} = 1 \) where \( \chi = \frac{{k_{30} k_{10}^{2} \sinh 2k_{10} h_{1} }}{{k_{10} k_{30}^{2} \sinh 2k_{30} h_{3} }}\left\{ {\frac{{2k_{30} h_{3} + \sinh 2k_{30} h_{3} }}{{2k_{10} h_{1} + \sinh 2k_{10} h_{1} }}} \right\} \).

4 Numerical Results and Discussions

The hydroelastic behaviour of the floating thick elastic plate under the action of incident wave is analysed based on Timoshenko–Mindlin theory in finite water depth. The study is performed to analyse the reflection coefficient \( K_{r} \), plate deflection \( \zeta_{j} \), bending moment \( \left| {M\left( x \right)} \right| \), shear force \( \left| {W\left( x \right)} \right| \) and strain on the plate \( \left| \varepsilon \right| \) for floating elastic plate with varying bottom topography. The numerical computations are carried out for different values of water depth \( h_{j} /L \), plate thickness \( d/L \), Young’s modulus \( E \) and wave frequency \( \omega \) considering \( E = 5\,{\text{GPa,}} \) \( \rho_{p} /\rho_{w} = 0.9, \) \( \nu = 0.3 \) and \( g = 9.8\,{\text{ms}}^{ - 2} \). In this analysis, the parameters such as plate length \( L = 500\,{\text{m}} \) and wave frequency \( \omega = 3\,{\text{s}}^{ - 1} \) are considered to be fixed unless otherwise mentioned. The water depths in reflected and transmitted regions are considered to be \( h_{1} = 100\,{\text{m and }}h_{3} = 100\,{\text{m}} \), respectively. The accuracy of the computed numerical results are checked with the energy relation which satisfies \( K_{r}^{2} + \chi K_{t}^{2} = 1. \)

4.1 Reflection and Transmission Coefficients

The reflection and transmission coefficients are plotted at varying wave frequency. The study shows the variations in reflected and transmitted waves due to the changes in bottom topography with varying wave frequency at varying water depths over plate-covered region as shown in Fig. 2a, b.

Fig. 2
figure 2

a Reflection and b transmission coefficient versus wave frequency for different values of water depths

Full size image

The zeros in the reflection coefficient indicate complete transmission of waves through the plate. The reflection and transmission coefficients value equal to unity implies that complete reflection or transmission of waves. It is observed that there is an increase in wave with the decrease in water depth which may be due to the increase in wave height at lower water depths. At lower frequencies, there is an increase in reflected waves, whereas at higher frequencies, transmission of waves is found to be higher.

4.2 Surface Deflection

The surface deflection along the length of the plate for varying plate thickness and varying water depths over plate-covered region are shown in Fig. 3a, b.

Fig. 3
figure 3

Plate deflection along the plate length at varying a plate thickness and b water depths with changing bottom topography

Full size image

It is clearly seen that the deflection increases at the edges of the plate and the deflection decreases with increase in plate thickness. This is due to the fact that with the increase in the plate thickness, the plate rigidity increases and as a result the deflection decreases. It is also observed that there is an increase in deflection with the decrease in water depth at 70 m and it is mainly due to the rise in wave height and reduction in wavelength as the waves approach shallower water depth.

4.3 Wave-Induced Strain on Floating Plate

The strain induced in the floating elastic plate due to the action of ocean waves are analysed for varying plate thickness and water depth along plate-covered region in Fig. 4a, b. The wave-induced strain decreases with the increase in plate thickness which is mainly due to an increase in the plate rigidity. The increase in the strain with the decrease in water depth at 70 m may be due to rise in wave height and reduction in wavelength as the waves approach shallow water depth.

Fig. 4
figure 4

Wave-induced strain versus plate length at varying a plate thickness and b water depths with changing bottom topography

Full size image

4.4 Bending Moment of Floating Plate

The bending moment resultants due to the wave interaction with the floating elastic plate are plotted at varying plate thickness and water depth in plate-covered region along the plate length in Fig. 5a, b. The bending moment resultant decreases with an increase in plate thickness mainly due to an increase in plate rigidity. It is found that bending moment increases with the decrease in water depth at 70 m due to rise in wave height and reduction of wavelength as the wave approaches shallow water depth.

Fig. 5
figure 5

Bending moment along the length of the plate at varying a plate thickness and b water depths with changing bottom topography

Full size image

4.5 Shear Force on Floating Plate

The shear force resultants due to the wave interaction with the floating elastic plate are plotted at varying plate thickness and water depth along the plate length in Fig. 6a, b. The shear force resultants decrease with an increase in plate thickness mainly due to the increase in plate rigidity. The shear force is found to increase with the decrease in water depth and may be due to rise in wave height as wave’s approaches shallow water depth.

Fig. 6
figure 6

Shear force along the length of the plate at varying a plate thickness and b water depths with changing bottom topography

Full size image

5 Conclusion

The hydroelastic behaviour of floating elastic plate based on Timoshenko–Mindlin’s plate theory under the action of ocean waves in finite water depths is analysed for changing bottom topography. The mathematical model using eigenfunction expansion method is developed for the freely floating elastic plate over changing bottom topography. The conclusions drawn from the present study are as follows:

  • The increase in the wave transmission is observed in the case of finite water depth for higher wave frequency.

  • Complete wave transmissions are observed at certain values of wave frequency and significant effect due to the change in water depth in the hydroelastic behaviour of floating elastic plate is observed which is mainly due to rise in wave height and reduction in wavelength.

  • A steep increase in hydroelastic behaviour is observed at lower water depths in plate-covered region may be mainly due to higher difference in water depth between the mediums of interaction.

  • The plate rigidity and plate thickness play an important role in the reduction of the hydroelastic behaviour of the plate.

  • At lower wave frequency, there is an increase in the hydroelastic behaviour of the plate, whereas no significant hydroelastic behaviour is observed at higher wave frequencies.