1 Introduction

The construction of floating flexible platforms is under consideration in several parts of the world. In the last few decades, the scientists and engineers have shown interest to analyse the transformation of incident wave energy by floating elastic structure, which can be modelled as a very large floating structure (VLFS), and these platforms may meet several wave calamities, ranging from sheltered areas to open areas. The study of VLFS is important because they can provide an alternate solution of the land scarcity, which is due to urban development increment in population in many countries. So in these countries, if they have long coastlines, the space of the ocean can be utilized by constructing such platform. The use of VLFS has been proposed by scientists and engineers for industrial space, habitation, storage facilities and airports in response to the above challenges. The advantage of using VLFS is that it is created artificially on the water body, and at the same time the effect of VLFS on tidal current flows and aquatic habitats is minimum. Hence, the study of scattering problems involving structural response of the floating flexible platforms is of great interest towards the safety and stability of these floating platforms. Sahoo et al. [35] have examined that the VLFS can be assumed as elastic structure because of the significance impact of vibration/localized deflection of the long structure due to the continuous excitation of wave having small amplitude. The motion of the structure is small as compared to its length. The theoretical study of the localization phenomenon of gravity waves by a rough bottom in a one-dimensional channel was studied by Devillard et al. [8]. The mathematical model for reflection and penetration of ocean waves into shore fast sea ice was developed by Fox et al. [9]. Further, the response of ice floes to ocean waves in both cases (infinite as well as the finite depth) was examined by Meylan et al. [29]. Moreover, Wang and Meylan [46] have investigated the response of linear wave on floating thin plate in the presence of variable depth with the aid of boundary element method. Several methods have been utilized towards the minimization of structure responses induced by waves during the last two decades. The review of these methods has been highlighted by Wang et al. [47]. Tkacheva [39] investigated the behaviour of a floating elastic strip-shaped plate by using the Wiener–Hopf technique. Further, the scattering of surface water waves by a floating semi-infinite elastic plate in a finite depth of water was considered by Sahoo et al. [35]. Evans and Porter [10] analysed the oblique wave scattering caused by a narrow crack in ice sheets floating over finite depth of water using the eigenfunction expansion method. Lamas-Pardo et al. [23] have discussed the recent developments on VLFS. Mohapatra and Sahoo [30] studied the performance of submerged structure to minimize the responses of VLFS. Mondal and Banerjea [31] have derived the results towards the wave energy dissipation by inclined porous plate below the ice cover. Recently, Cheng et al. [4] studied the interaction of irregular waves with structure having inclined perforated plates with the aid of hybrid finite element-boundary element method and eigenfunction matching method in the context of time-domain theory. The problem involving propagation of oblique incident wave passing through breakwater was examined by Chen et al. [3] with the aid of an adaptive mesh scheme in boundary element method . Chakrabarti [2] analysed the problem of scattering of surface water waves by the edge of an ice cover and obtained the explicit solution with a singular, Carleman-type integral equation. Cho and Kim [5] studied the interaction of oblique incident waves with a horizontal flexible membrane in a finite depth of water and found that a properly designed horizontal flexible membrane can be an effective wave barrier. The defection of a large floating flexible platform was determined by Hermans [12] with the aid of an integro-differential equation. Hermans [13] has examined the problem of interaction of waves with a rigid or flexible dock with zero drafts. Further, the hydroelastic response of a two-dimensional very large floating platform to an incident plane wave was investigated for three different cases: shallow water depth and finite as well as infinite depth by Andrianov et al. [1]. The integral equation approach with the aid of Green’s integral theorem has been utilized by Maiti et al. [26] to solve the problem of wave interaction with thin vertical plate submerged beneath the ice cover. The wave generation problem for viscous fluid of finite depth due to an axisymmetric initial surface disturbance was investigated by Kundu et al. [22]. The problem involving hydrodynamic interaction between two ships advancing in waves was discussed by Yuan et al. [50] with the aid of rapid method. Further, expansion formulae in wave structure interaction problems were derived by Manam et al. [27]. The problem involving scattering and radiation of surface water waves by a finite dock floating over an asymmetric rectangular trench-type was analysed by Choudhary et al. [6] with the aid of eigenfunction expansion method along with boundary element method. Further, the problem of wave structure interaction with thick vertical barrier over an arbitrary seabed was analysed for its solution with the help of coupled eigenfunction expansion method by Choudhary et al. [7]. Moreover, in the case of step-type bottom topography, oblique flexural gravity-wave interaction in the presence of a compressive force was investigated by Karmakar et al. [16] based on the linearized water-wave theory. The problem involving oblique surface gravity wave scattering by a floating flexible porous plate was investigated by Koley et al. [19] with the aid of integral equation approach. The problem of mitigation of structural responses of a very large floating structure in the presence of vertical porous barrier was studied by Singla et al. [37]. A new model was presented for the propagation of monochromatic surface waves over a region of arbitrary bottom topography by O’Hare et al. [32] where the wave fields on either side of each step were related by a transfer matrix and the propagation of waves along the shelf between adjacent steps was described by a rotation matrix. Further, the comparisons between two models for surface-wave propagation over rapidly varying bottom topography, one based on the extended-mild-slope equation and the other on the successive-application-matrix model, was described by O’Hare et al. [33]. An indirect eigenfunction marching method (IEMM) was developed by Tsai et al. [41] to provide step approximations for water-wave problems where they shown that the solutions obtained by the IEMM converge very well to Roseau’s analytical solutions for both mild and steep curved bottom profiles. Further, the problem of water-wave scattering by steep slopes was studied by Tsai et al. [42] with the extension of Miles’s variational formulation. In the same context, for simulating the propagation of small-amplitude water waves over variable bathymetry, Tsai et al. [43] utilized the consistent coupled-mode system (CCMS) and the eigenfunction matching method (EMM). For the CCMS, a bottom-sloping mode is coupled in the mild-slope equation with evanescent modes, and for the EMM, the bottom profile is approximated in terms of successive flat shelves separated by abrupt steps. Moreover, the problem involving interaction of waves with tension leg structures over uneven bottoms was studied by Tsai et al. [44]. Wave reflection by a submerged rectangular breakwater with two scour trenches is explored by Liu et al. [25] with the aid of modified mild-slope equation. Linear long-wave reflection by a rectangular obstacle with two scour trenches of power function profile is explored by Xie et al. [48]. An exact analytic solution to the modified mild-slope equation (MMSE) in terms of Taylor series for waves propagating over an asymmetrical trench with various shapes was developed by Xie et al. [49]. The problem of propagation of obliquely incident surface water waves involving an asymmetric rectangular trench in a channel of finite depth was examined for its solution by Kaur et al. [18]. The problem involving exciting forces for an arrangement of two coaxial vertical cylinders, i.e. a riding porous cylinder and a submerged bottom-mounted solid rigid cylinder, is investigated by Sarkar et al. [36]. Recently, oblique wave scattering and trapping by a partial porous breakwater in the presence of seabed undulation are studied by Tabssum et al. [38]. The problem of scattering of obliquely incident gravity waves by a horizontal floating flexible porous plate in the water of finite depth having a variable bottom bed was studied by Koley [20] where the coupled eigenfunction expansion-boundary element method is used for the solution purpose. In the same direction, the problem involving the performance of a submerged flexible porous membrane placed at a finite distance away from a partially reflecting seawall was investigated by Koley et al. [21] where the solution of the problem was handled by dual boundary element method. Furthermore, the effect of an undulated bottom topography on the radiation of water waves by a floating rectangular buoy was analysed by Trivedi [40]. In the context of Bragg resonance, the problem involving Bragg resonance due to scattering of long gravity waves by an array of submerged trenches in the presence of the sloping sea bed was discussed by Kar et al. [15]. Further, the effect of Bragg resonance due to the scattering of surface waves by an array of trenches or breakwaters irrespective of the presence of the floating semi-infinite plate was studied by Kar et al. [14]. Also, the Bragg reflections of oblique water waves by periodic surface-piercing structures over periodic bottoms are investigated by Tseng et al. [45]. In the above studies, the study of flexible plate over uneven bottom is limited. So in the present work, an effort has been made towards the study of transformation of incident wave energy by an elastic plate situated at a finite distance from an arbitrary bottom topography with the aid step approximation method along with eigenfunction expansion method. The values of hydrodynamic quantities, namely reflection and transmission coefficients and deflection of plate are calculated for various values of structural and system parameters such as length of elastic plate, water depth ratios, angle of incidence, distance between the elastic plate and bottom topography. The present results have been validated with the known results in the literature for the case of rigid floating structure. The energy identity is obtained through Green integral theorem and is checked in towards the accuracy of present results.

2 Mathematical formulation of the problem

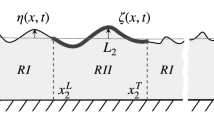
The interaction of water wave with an elastic plate, which is placed at a finite distance from bottom topography, is examined for its solution in three-dimensional space. Here, the bottom topography is considered to be arbitrary in nature. In this co-ordinate system, y-axis is positive downward and \(xz-\) horizontal plane represents the undisturbed free surface. The floating elastic plate placed at the position \(y=0,\; b \le x \le c\) has finite length (\(c-b\)) and negligible thickness. Due to the infinity long floating structure in the z-direction, the characteristic behaviour of the structure will remain the same along z-axis. Here, \(y= H(x)\) represents the arbitrary bottom profile, which is asymmetric in nature. Here \(H(x) =h(x),\;-l \le x \le l\) with \(l < b\) and \(H(x) = h_1,\; x \le -l\) and \(H(x) = {\hat{h}}_{1},\; x \ge l\) (see Fig. 1). The depth \(h_1\) before the profile and depth \({\hat{h}}_{1}\) after the uneven bottom are not equal. When \(h_1= {\hat{h}}_{1}\), i.e. the profile is symmetric. Here, to approximate this profile \(m-1\) number of steps are considered in upward direction as well as in downward direction. However, it is not required to consider the equal number of steps in both directions. Hence, in the interval in \(-l\le x \le 0\), \(m-1\) shelves are created, which are given by \(-a_{i} \le x \le -a_{i-1}\) with depth \(h_{(m+1)-i},\;i=1,2, \dots , m-1\). Similarly, in the interval \( 0 \le x \le l\), \(m-1\) shelves are created, which are given by \(a_{i-1} \le x \le a_{i}\) with depth \(h_{m+i},\; i=1,2, \dots , m-1\) where \(l=a_{m-1}\). So, in the interval \([-l,0]\), there are \(m-1\) steps at \(x= -a_{i},\; i=1,2, \dots , m-1\), and in the interval [0, l] there are \(m-1\) steps at \(x=a_{i},\; i=1,2,\dots , m-1\) (see Fig. 1). Hence, the whole fluid domain can be composed of \(2m+2\) regions, which are given as \(R_1\): { \(-\infty \le x \le -l=-a_{m-1},\; 0 \le y \le h_1 \)}; region \(R_2\) : { \(-l=-a_{m-1} \le x \le -a_{m-2},\; 0 \le y \le h_2 \)}; regions \(R_{j}\;(j=3,4, \dots m)\) are \(\{-a_{m+1-j} \le x \le -a_{m-j},~ 0 \le y \le h_{j},\;j=3,4,\dots , m \}\); regions \(R_{j}\; (j=m+1,m+2,\dots 2m-1)\) are \(\{a_{{j}-(m+1)} \le x \le a_{{j}-m}, 0 \le y \le h_{j},\;{j}= m+1,m+2, \dots , 2m-1 \}\); region \(R_{2m}\) is {\(a_{m-1}=l \le x \le b,~ 0 \le y \le h_{2m}={\hat{h}}_{1}\}\); region \(R_{2m+1}\) is {\(b \le x \le c,~ 0 \le y \le {\hat{h}}_{1}\}\) and the last region \(R_{2m+2}\) is {\(c \le x \le \infty ,~ 0 \le y \le {\hat{h}}_{1}\}\) (see Fig. 1). In Fig. 1,

$$\begin{aligned} {\left\{ \begin{array}{ll} h_{i} \ge h_{i+1}, i=1,2, \dots m-1\\ h_{i} = h_{i+1},i=m \\ h_{i} \le h_{i+1},i=m+1,m+2,\dots 2m-1. \end{array}\right. } \end{aligned}$$
(1)
Fig. 1
figure 1

Schematic of the step approximation

Full size image

For an inviscid and incompressible fluid where the fluid motion is considered to be irrotational and simple harmonic in time t, the incident velocity potential is given by:

$$\begin{aligned} \Phi ^{inc}(x,y,z,t)= & {} \Re \{ \phi ^{inc} (x,y) e^{\varvec{\iota } (\nu z- \omega t)}\}, \end{aligned}$$
(2)
$$\begin{aligned} \text {where}~~ \phi ^{inc}(x,y)= & {} \frac{\cosh k_{1,0}(y-h_1)}{\cosh k_{1,0}h_1} e^{\varvec{\iota } {\tilde{k}}_{1,0}}, \end{aligned}$$
(3)

where \(\Re \{.\}\) denotes the real part, \(\omega \) is the angular frequency, \(\theta \) is the angle of incidence.

Here, \(x-\) component of the incident wave is given by:

$$\begin{aligned} {\tilde{k}}_{1,0}=k_{1,0}\cos \theta = +\sqrt{(k_{1,0})^2-\nu ^2} \end{aligned}$$
(4)

and \(z-\) component of the incident wave is given by

$$\begin{aligned} \nu =k_{1,0}\sin \theta . \end{aligned}$$
(5)

Further, \(k_{1,0}\) is the unique positive root of the transcendental equation in k as given by

$$\begin{aligned} K-k_{1,0}\tanh k_{1,0} h_1=0. \end{aligned}$$
(6)

Now, in each region \(R_j, (j=1,2,\ldots 2m+2)\), the velocity potential can be written as:

$$\begin{aligned} \Phi _j(x,y,z,t)=\Re \{\phi _j(x,y)\mathrm {e}^{-\varvec{\iota } \omega t +\varvec{\iota } \nu z}\},~j=1,2,3, \dots ,2m+2. \end{aligned}$$
(7)

Here, in each fluid region \(R_j\), \(j=1,2,\dots ,2m+2\), \(\phi _j(x,y)\) satisfies

$$\begin{aligned} \frac{\partial ^2 \phi _j}{\partial x^2}+\frac{\partial ^2 \phi _j}{\partial y^2}-\nu ^2 \phi _j = 0.~~ \end{aligned}$$
(8)

In open water region, the linearized free surface condition is given by:

$$\begin{aligned} \frac{\partial \phi _j}{\partial y}+ K \phi _j = 0,~~ \text {on}~~ y=0,~ -l<x<b,~~ \text {and}~~ c< x < \infty ,~~ \end{aligned}$$
(9)

where \(j=1,2, \ldots 2m, 2m+2\) and \(K=\omega ^2 / g\) and g is an acceleration due to gravity.

The boundary condition on the floating elastic plate is given by (ref. Mandal et al. [28]):

$$\begin{aligned} \left[ D \left( \frac{\partial ^2}{\partial x^2}- \nu ^2\right) ^2 +1-\epsilon K\right] \frac{\partial \phi _{2m+1}}{\partial y} + K \phi _{2m+1} =0 ~~\text {on} ~~y=0, b<x<c, \end{aligned}$$
(10)

where \(D =EI/\rho g\) is the flexural rigidity of the plate with E is the effective Young’s modulus of the elastic plate, \(I= d^3/12(1-\nu _0^2)\) with \(\nu _0\) as Poisson’s ratio, d is the thickness of the plate, \(\epsilon =\rho _s d/ \rho \) with \(\rho _s\) is the density of the elastic plate and \(\rho \) is the density of the fluid. Moreover, the condition (10) will give rise to the free surface condition (9) when \(D=0, \epsilon =0\).

Since, the elastic plate is freely floating, hence at the edges of the plate, the shear force and bending moment will vanish which is given by:

$$\begin{aligned}&\left( \frac{\partial ^2}{\partial x^2 }-\nu _0 \nu ^2\right) \frac{\partial \phi _{2m+1}}{\partial y} \rightarrow 0,~ \text { and}~~\frac{\partial }{ \partial x }\left( \frac{\partial ^2 }{\partial x^2 }-(2-\nu _0) \nu ^2 \right) \frac{\partial \phi _{2m+1}}{\partial y} \rightarrow 0~\text { at}~ x=b, \end{aligned}$$
(11)
$$\begin{aligned}&\left( \frac{\partial ^2}{\partial x^2 }-\nu _0 \nu ^2\right) \frac{\partial \phi _{2m+1}}{\partial y} \rightarrow 0,~ \text { and}~~\frac{\partial }{ \partial x }\left( \frac{\partial ^2 }{\partial x^2 }-(2-\nu _0) \nu ^2 \right) \frac{\partial \phi _{2m+1}}{\partial y} \rightarrow 0~\text { at}~ x=c. \end{aligned}$$
(12)

In region \(R_1; \phi _1\) satisfies

$$\begin{aligned} \frac{\partial \phi _1}{\partial y}= & {} 0 ~~ \text {on}~ y = h_1,\; -\infty < x \le -l= -a_{m-1}, \end{aligned}$$
(13)
$$\begin{aligned} \frac{\partial \phi _1}{\partial x}= & {} 0 ~~ \text {at}~ x = -a_{m-1},\; h_2 \le y \le h_1. \end{aligned}$$
(14)

In each region \(R_{j}\)  where \(j=2, 3, \dots , m,~\phi _j\) satisfies

$$\begin{aligned} \frac{\partial \phi _j}{\partial y}= & {} 0 ~~ \text {on}~ y = h_{j},\;-a_{m+1-j} \le x \le -a_{m-j}, \end{aligned}$$
(15)
$$\begin{aligned} \frac{\partial \phi _j}{\partial x}= & {} 0~~ \text {on}~ x=-a_{m-j},\;h_{j+1} \le y \le h_{j}. \end{aligned}$$
(16)

In each region \(R_{{j}}\) where \({j}=m+1,m+2, \dots , 2m-1, 2m ,~\phi _{{j}}\) satisfies

$$\begin{aligned} ~\frac{\partial \phi _{{j}}}{\partial y}= & {} 0 ~~ \text {on}~ y = h_{{j}},\;~a_{{j}-(m+1)} \le x \le a_{{j}-m}, \end{aligned}$$
(17)
$$\begin{aligned} \frac{\partial \phi _{{j}}}{\partial x}= & {} 0,~~ \text {on}~ x=a_{{j}-(m+1)},~ h_{{j-1}} \le y \le h_{{j}} \quad ~with~ \quad a_{m-1} =l, a_{m}=b,~~ {\hat{h}}_{1} =h_{2m}. \end{aligned}$$
(18)

In region \(R_{2m+1},~ \phi _{2m+1}\) satisfies

$$\begin{aligned} \frac{\partial \phi _{2m+1}}{\partial y}= & {} 0~~ \text {on}~ y={\hat{h}}_{1},~ b< x \le c. \end{aligned}$$
(19)

In region \(R_{2m+2},~ \phi _{2m+2}\) satisfies

$$\begin{aligned} \frac{\partial \phi _{2m+2}}{\partial y}= & {} 0~~ \text {on}~y={\hat{h}}_{1},~ c< x < \infty . \end{aligned}$$
(20)

In regions \(R_1\) & \(R_{2m+2}\), the scattered velocity potential \(\phi _1(x,y)\) and \(\phi _{2m+2}(x,y)\), respectively, satisfies the far-field conditions:

$$\begin{aligned}&\phi _{1}(x,y) \displaystyle \rightarrow \left( \mathrm { e}^{\varvec{\iota } {\tilde{k}}_{1,0} (x + l)} + R \mathrm {e}^{-\varvec{\iota } {\tilde{k}}_{1,0} (x + l)}\right) \frac{\cosh k_{1,0}(y-h_1)}{\cosh k_{1,0}h_1}~~ \text {as}~~ x \rightarrow - \infty , \end{aligned}$$
(21)
$$\begin{aligned} \text {and}~&\phi _{2m+2}(x,y) \displaystyle \rightarrow T \mathrm {e}^{\varvec{\iota } {\tilde{k}}_{2m,0} (x - l)} \frac{\cosh k_{2m,0}(y-{\hat{h}}_{1})}{\cosh k_{2m,0} {\hat{h}}_{1}}\text {as}~~ x \rightarrow \infty , \end{aligned}$$
(22)

where

$$\begin{aligned} {\tilde{k}}_{2m,0}=+\sqrt{(k_{2m,0})^2-\nu ^2} \end{aligned}$$
(23)

and \( k=k_{2m,0}\) is the unique positive root of the transcendental equation

$$\begin{aligned} k_{2m,0}\tanh k_{2m,0} {\hat{h}}_{1} =K. \end{aligned}$$
(24)

Here, T and R are the unknown complex constants associated with the amplitudes of transmitted and reflected waves, respectively.

3 Method of solution

To solve the associated mixed boundary value problem involving Eqs. (8)–(22), matched eigenfunction expansion method is applied. In each region \(R_j\), the velocity potential \(\phi _{j},\;(j=1,2,\dots 2m+2)\) is given by Havelock’s expansion [11] formulas as

$$\begin{aligned} \phi _{1}(x,y)= & {} \displaystyle \left( \mathrm {e}^{\varvec{\iota } {\tilde{k}}_{1,0} (x + l)} + R\; \mathrm {e}^{-\varvec{\iota } {\tilde{k}}_{1,0} (x + l)}\right) \psi _{1,0}(y) +\sum _{n=1}^{\infty }A_n e^{{\tilde{k}}_{1,n}(x+l)}\psi _{1,n}(y), \nonumber \\&-\infty< x \le =-a_{m-1} =-l, ~0<y<h_1, \end{aligned}$$
(25)
$$\begin{aligned} \phi _j(x,y)= & {} \displaystyle \sum _{n=0}^{\infty }\left( B_{j,n} e^{{\tilde{k}}_{j,n} (x+a_{m+1-j})}+C_{j,n}e^{-{\tilde{k}}_{j,n} (x+a_{m-j})}\right) \psi _{j,n}(y), \nonumber \\&j=2,3,\dots , m~\text {and}~ -a_{m+1-j} \le x \le -a_{m-j}, ~0<y<h_{j}, \end{aligned}$$
(26)
$$\begin{aligned} \phi _{{j}}(x,y)= & {} \displaystyle \sum _{n=0}^{\infty }\left( B_{j,n} e^{{\tilde{k}}_{j,n} (x-a_{{j}-(m+1))}}+C_{j,n} e^{-{\tilde{k}}_{j,n} (x-a_{(j-m))}}\right) \psi _{j,n}(y), \nonumber \\&{j}=m+1,m+2 \dots , 2m-1, 2m ~ \text {and} ~a_{{j}-(m+1)} \le x \le a_{j-m}, ~0<y<h_{j}, \end{aligned}$$
(27)
$$\begin{aligned} \phi _{2m+1}(x,y)= & {} \displaystyle \sum _{n=-2, -1}\left( B_{2m+1,n} \;\mathrm {e}^{{\tilde{p}}_{n} (x-b)}+C_{2m+1,n} \;\mathrm {e}^{ -{\tilde{p}}_n (x-c)}\right) g_{2m+1,n}(y) \nonumber \\&+ \sum _{n=0}^{\infty }\left( B_{2m+1,n} \;\mathrm {e}^{ {\tilde{p}}_n (x-b)}+C_{2m+1,n}\;\mathrm {e}^{-{\tilde{p}}_n (x-c)}\right) g_{2m+1,n}(y), \nonumber \\&b \le x \le c, ~0<y<{\hat{h}}_{1}, \end{aligned}$$
(28)
$$\begin{aligned} \phi _{2m+2}(x,y)= & {} \displaystyle T \;\mathrm {e}^{\varvec{\iota } {\tilde{k}}_{2m,0} (x - c)} \psi _{2m,0}(y) +\sum _{n=1}^{\infty }D_n\; \mathrm {e}^{-{\tilde{k}}_{2m,n}(x-c)} \psi _{2m,n}(y), \nonumber \\&c \le x< \infty , ~0<y<{\hat{h}}_{1}, \end{aligned}$$
(29)
$$\begin{aligned} \psi _{j,n}(y)= & {} \frac{\cos k_{j,n}(y-h_j)}{ \cos k_{j,n}h_j}, \qquad j=0,1,2,3,\dots , 2m~ \text {and}~ n=1,2,\dots ,\end{aligned}$$
(30)
$$\begin{aligned} g_{2m+1,n}(y)= & {} \frac{\cos p_n(y-{\hat{h}}_{1})}{\cos p_n {\hat{h}}_{1}}, \qquad n=-2,-1,0,1,2,3,\dots . \end{aligned}$$
(31)

with relation

$$\begin{aligned} {\tilde{k}}_{j,0}=\varvec{\iota }{\tilde{k}}_{j,0}~~~j=2,3,\ldots 2m \end{aligned}$$

and

$$\begin{aligned} {\tilde{p}}_0 =\varvec{\iota } {\tilde{p}}_0 \end{aligned}$$

Also,

$$\begin{aligned} {\tilde{k}}_{j,0}=+\sqrt{(k_{j,0})^2-\nu ^2},~~{\tilde{k}}_{j,n}=+\sqrt{(k_{j,n})^2+\nu ^2}, \end{aligned}$$
(32)

where \(k_{j,0}\) are the positive real roots of the transcendental equation

$$\begin{aligned} k_{j,0} \tanh k_{j,0} h_j=K,~~ j=1,2, \dots 2m, \end{aligned}$$
(33)

and \(k_{j,n}\) are the real roots of the transcendental equation

$$\begin{aligned} k_{j,n} \tan k_{j,n} h_j=-K,~~ j=1,2, \dots 2m,~~n=1,2, \dots \end{aligned}$$
(34)

Also, \( {\tilde{p}}_{0}=+\sqrt{(p_0)^2-\nu ^2}\) where \(p_{0}\) is the positive real root of the following transcendental equation in p in plate covered region:

$$\begin{aligned} (D p^4 +1-\epsilon K) p \tanh p \hat{h_{1}}= K, \end{aligned}$$
(35)

and \({\tilde{p}}_n=+\sqrt{(p_n)^2+\nu ^2}\) where \(p_{n}\) for \(n=-2,-1\) are complex conjugate roots having positive real parts and \(p_n\) for \( n=1,2,\ldots ,\) are the real roots of the dispersion relation over the plate covered region

$$\begin{aligned} (D p^4 +1-\epsilon K) p \tan p \hat{h_{1}}= -K. \end{aligned}$$
(36)

In above expansions (25)–(29), \(T,~R,~A_n,~ B_{j,0},~ B_{j,n},~ C_{j,0},~C_{j,n},~ D_{n},\;j=2,3, \dots , 2m+1,\;n=1,2,3 \dots \) and \(B_{n, 2m+1}, ~C_{n, 2m+1}, ~~n=-2,-1\) are unknown complex constants to be determined.

Define \(h_j^{min}=\text {min}(h_j,h_j+1);~\text {amd}~h_j^{max}=\text {max}(h_j,h_j+1);~~ j=1,2,\ldots 2m\). Here, \(h_{2m}=h_{2m+1}=h_{2m+2}.\)

The matching conditions, i.e. continuity of pressure and velocity along each interface,

$$\begin{aligned} {\left\{ \begin{array}{ll} 0<y<h_j^{min};~~ x = -a_{m-j},\;j=1, 2,\dots , m\\ 0<y<h_j^{min};~~ x = a_{j-m},\;j=m+1,m+2,\dots ,2m\\ 0<y<{\hat{h}}_1;~~ x =c\\ \end{array}\right. } \end{aligned}$$
(37)

are given by

$$\begin{aligned} \phi _{j}= & {} \phi _{j+1}, \end{aligned}$$
(38)
$$\begin{aligned} \frac{\partial \phi _j}{\partial x}= & {} \frac{\partial \phi _{j+1}}{\partial x}. \end{aligned}$$
(39)

Further, the orthogonality of eigenfunctions is used to obtain the following equations. For \(j=1,2,3, \dots m\) and \(n=0,1,2,\dots , N\)

$$\begin{aligned} {\left. \begin{aligned}&\int _0^{h_{j}^{min}}{\phi _j(-a_{m-j},y)\psi _{j,n}(y)}~ dy= & {} \int _0^{h_{j}^{min}}{\phi _{j+1}(-a_{m-j},y)\psi _{j,n}(y)}~ dy , \nonumber \\&\int _0^{h_{j}^{max}}{\phi _{j x}(-a_{m-j},y)\psi _{j+1,n}(y)}~ dy= & {} \int _0^{h_{j}^{min}}{\phi _{(j+1) x}(-a_{m-j},y)\psi _{j+1,n}(y)} ~dy, \end{aligned}\right\} }\\ \end{aligned}$$
(40)

For \(j=m+1,m+2, \dots 2m-1,2m, 2m+2\) and \(n=0,1,2,\dots , N\)

$$\begin{aligned} {\left. \begin{aligned}&\int _0^{h_{j}^{min}}{\phi _j(a_{j-m},y)\psi _{j+1,n}(y)}~ dy= & {} \int _0^{h_{j}^{min}}{\phi _{j+1}(a_{j-m}, y)\psi _{j+1,n}(y)}~ dy, \nonumber \\&\int _0^{h_{j}^{max}}{\phi _{j x}(a_{j-m},y)\psi _{j,n}(y)}~ dy= & {} \int _0^{h_{j}^{min}}{\phi _{(j+1) x}(a_{j-m},y)\psi _{j,n}(y)} ~dy, \end{aligned}\right\} }\\ \end{aligned}$$
(41)

Here, \(a_m=b, a_{m+1} =c\) and \(\psi _{2m+1,n}(y)=\psi _{2m+2,n}(y)=\psi _{2m,n}(y)\) are considered.

Substituting Eq. (28) in the free edge conditions given by Eqs. (11) and (12) gives rise to the following set of four equations

$$\begin{aligned}&p_{0}\left( ({\tilde{p}}_0)^2+\nu _0 \nu ^2\right) \left( B_{j,0}+c_{0,j} e^{-i\varvec{\iota } {\tilde{p}}_0(b-c)}\right) \tanh p_0 {\hat{h}}_1 +\nonumber \\&\sum _{n=-2,-1,n=1}^{\infty } p_n\left( ({\tilde{p}}_n)^2-\nu _0 \nu ^2 \right) \left( B_{j,n} +C_{j,n} e^{-{\tilde{p}}_n (b-c)}\right) \tan p_n \hat{h_1}=0, \end{aligned}$$
(42)
$$\begin{aligned}&i{\tilde{p}}_0p_{0}\left( ({\tilde{p}}_0)^2+(2-\nu _0) \nu ^2\right) \left( B_{j,0}-C_{j,0} e^{-\varvec{\iota } {\tilde{p}}_0(b-c)}\right) \tanh p_0 {\hat{h}}_1+ \nonumber \\&\sum _{n=-2,-1,n=1}^{\infty } {\tilde{p}}_np_n\left( ({\tilde{p}}_n)^2-(2-\nu _0) \nu ^2 \right) \left( B_{j,n} -C_{j,n} e^{-{\tilde{p}}_n (b-c)}\right) \tan p_n \hat{h_1}=0, \end{aligned}$$
(43)
$$\begin{aligned}&p_{0}\left( ({\tilde{p}}_0)^2+\nu _0 \nu ^2\right) \left( B_{j,0}e^{i{\tilde{p}}_0(c-b)}+C_{j,0} \right) \tanh p_0 {\hat{h}}_1 + \nonumber \\&\sum _{n=-2,-1,n=1}^{\infty } p_n\left( ({\tilde{p}}_n)^2-\nu _0 \nu ^2 \right) \left( B_{j,n}e^{{\tilde{p}}_n (c-b)} +C_{j,n} \right) \tan p_n \hat{h_1}=0, \end{aligned}$$
(44)
$$\begin{aligned}&i{\tilde{p}}_0p_{0}\left( ({\tilde{p}}_0)^2+(2-\nu _0) \nu ^2\right) \left( B_{j,0} e^{\varvec{\iota } {\tilde{p}}_0(c-b)}-C_{j,0}\right) \tanh p_0 {\hat{h}}_1 +\nonumber \\&\sum _{n=-2,-1,n=1}^{\infty } {\tilde{p}}_np_n\left( ({\tilde{p}}_n)^2-(2-\nu _0) \nu ^2 \right) \left( B_{j,n}e^{{\tilde{p}}_n (c-b)} -C_{j,n}\right) \tan p_n \hat{h_1}=0. \end{aligned}$$
(45)

In these Eqs. (40)–(45), the series is truncated up to N (say). Further Eqs. (25)–(29) produce a system of \((4m+2)N+(4m+6)\) linear algebraic equations with \((4m+2)N+(4m+6)\) unknowns, which need to be solved to get the unknowns \(R,~ A_n,~ B_{j,0},~B_{j,n},~ C_{j,0}, ~C_{j,n},\) \(~D_{n}, T, B_{2m+1,-2}, C_{2m+1,-2}, B_{2m+1,-1}, C_{2m+1,-1}\) where \(j=2,3, \dots , 2m+1~ \text {and}~ n=1,2,\dots , N.\)

Once, the system of equations is solved, we can get \(\phi _{2m+1},\) and hence, we can determine the important quantities such as deflection, strain and shear force as given by the following relations.

Plate deflection: The deflection of elastic plate at \(y=0, b<x<c\) is given by (see Singla et al. [37]

$$\begin{aligned} \eta _{2m+1}=\left. \frac{-\varvec{\iota } \omega }{g} \phi _{2m+1}\right| _{y=0}. \end{aligned}$$
(46)

Strain and Shear force: On the plate surface, the non-dimensional surface strain \(S_t\) and shear force \(S_f\) are given by (see Singla et al. [37])

$$\begin{aligned} S_t= & {} \frac{\epsilon }{2 \omega } \left| \frac{\partial ^3 \phi _{2m+1}}{\partial x^2 \partial y}\right| _{y=0}, \end{aligned}$$
(47)
$$\begin{aligned} S_f= & {} \frac{D}{{\hat{h}}_1 \omega }\left| \frac{\partial ^4 \phi _{2m+1}}{\partial x^3 \partial y}\right| _{y=0}. \end{aligned}$$
(48)

4 Results and discussion

In this section, the hydrodynamic quantities, namely reflection coefficient (|R|), transmission coefficient (|T|), plate deflection \(\Re (\eta _{2m+1})\), strain (\(S_t\)) and shear force \((S_f)\), experienced by the elastic plate are determined for various values of system parameters. Here, all the structural and system parameters are non-dimensionalized by using length scale \(h_1\). The non-dimensional parameters are given by flexural rigidity \(D/{h_1}^4\) , thickness of the plate \(\epsilon /h_1,\) wavelength of incident wave \(\lambda = 2\pi /k_0 \), \(\hat{a_j}={a_j}/{h_{1}},\; j=1,2,\ldots m-1,\; {\hat{b}}= b/h_{1}, {\hat{c}}= c/h_{1},\;~ K_1 = Kh_1\) and \(H_j = {h_j}/{h_1},\;j=1,2,\ldots 2m\) are used for numerical computations.

The values of \(D/{h_1}^4 = 10, \;\epsilon /h_1 = 0.01\), \({\hat{l}}={\hat{a}}_{m-1}=1.0, \;{\hat{b}}=2.0,\; {\hat{c}}=3.0,\;H_{1}= 1.0,\;H_{2m}=0.7\), \(H_{m}=H_{m+1}=1.2\) (since \(H_{m} \le H_{2m}\)) and \(\theta =\pi /4\) are fixed in this study unless otherwise stated. The other depth ratios \(H_{j},\;(j=2,3,\dots ,m-1,m+2,m+3,\dots 2m-1)\) are calculated using different formulas depending upon the type of irregular topography. Several computational results are performed to analyse the effect of various system parameters, but in the subsequent section, few results are shown to avoid the similar behaviour of figures.

4.1 Convergence study for m and N

The convergence on m (number of successive steps either in downward direction or in upward direction) and N (number of evanescent modes) is examined for symmetric parabolic hump type bottom profile (see Fig. 2) given by the following equation:

$$\begin{aligned} H(x)={\left\{ \begin{array}{ll} h_1, \quad x< -l,\\ h(x) = h_{c}\left( 1-\frac{x^2}{\alpha ^2}\right) ,-l \le x < l,\\ {\hat{h}}_{1}, \quad l\le x, \end{array}\right. } \end{aligned}$$
(49)

where \(\alpha = \frac{a}{\sqrt{\frac{h_1}{h_{c}}-1}}\). After approximating the parabolic hump bottom profile using steps, we get \(h_c=h_m\).

Fig. 2
figure 2

Asymmetric parabolic hump bottom profile

Full size image

For convergence of N,  we fix \(m =220\) and the values of |R| are determined against \(K_1\) for various values of \(N = 1, 5, 10, 15, 20\) and 25 (see Table 1). The table shows that the same values of |R| are obtained up to three decimal places for \( N= 15,~20 ~ \& ~ 25\) for fixed values of \(K_1\). Hence, \(N =15\) is considered throughout the study.

Table 1 Numerical values of |R| for different values of N with fixed value of \(m=220\)
Full size table

For convergence of m, the number of evanescent modes N is fixed as 15 and \( |R|~ \& ~ |T|\) are calculated for different values of \(m=40, 130, 220, 280\) and 300 (see Table 2). Table 2 shows that same values of |R| and |T| are obtained up to three decimal places for \( m =220, 280 ~ \& ~ 300\) for fixed values of \(K_1\). Hence, for all numerical calculations related to parabolic bottom, \(m=220\) and \(N=15\) are considered throughout this study unless otherwise stated.

4.2 Validation

(a) Rigid dock over flat bottom topography

To validate the present results with Linton [24] for a rigid dock over flat bottom (ref. Fig. 3), the depth ratios \(H_j = 1 ~ (j=1,2,3,\dots ,2m)\), \({\hat{b}}=1.0,\;{\hat{c}}=2.0, D/h_1^4 =10^{10}\) and \(\theta =\pi /4\) are considered in the given problem. The results are well matched (Fig. 4 and Table 3) with the results by Linton [24] who used the modified residue calculus technique for this particular case. Here also we have validated the present proposed method with the results of Kaur et al. [17] in the case of rigid dock over flat bottom as a particular case of convex parabolic bottom topography who utilized the method of step approximation to solve the problem.

Fig. 3
figure 3

Finite rigid dock over flat bottom

Full size image
Fig. 4
figure 4

Comparison: |R| and |T| versus \(K_1\) when we fixed \(H_{j} = 1,j=1,2,\dots , 2m.\)

Full size image

(b) Elastic plate over flat bottom topography

Further, to validate the present results with Herman [13] for a elastic thin structure over flat bottom, the depth ratios \(H_j = 1 ~ (j=1,2,3,\dots ,2m)\), \(L={\hat{b}}-{\hat{c}}=30\) (length of elastic plate), \(D/h_1^4 =10^{-3}\) and \(\theta =0^{o}\) are considered in the present problem. Figure 5 shows that results are in good agreement with the results produced by Herman [13] where the Green function approach was utilized to obtain the solution.

Fig. 5
figure 5

|R| and |T| versus \(\lambda /L\) for elastic plate over flat bottom topography

Full size image

(c)Wave scattering over arbitrary bottom topography

Here, the proposed method is applied to solve the scattering of water waves over the undulated bottom profile in the absence of elastic plate. We consider a particular case of arbitrary bottom profile as discussed in Porter and Porter [34] and Tsai et al. [44], which is given by

$$\begin{aligned} H(x)={\left\{ \begin{array}{ll} h_1, \quad x \le -l\\ h(x) =h_m-(h_m-h_1)\left( 1-3\left( \frac{l-x}{l} \right) ^2 +2\left( \frac{l-x}{l} \right) \right) , \quad -l \le x \le 0,\\ h_m, \quad 0 \le x, \end{array}\right. } \end{aligned}$$
(50)

Here, l is the length of the undulated bottom. We have taken \(m=60\) to approximate the bottom profile.

Fig. 6
figure 6

|R| versus \(k_{1,0}h_1\) for undulated bottom profile in case of \(l/(h_m - h_1) = 8\) and \(h_m/h_1 = 2/5.\)

Full size image

Figure 6 shows that the values for |R| are well matched with the results obtained by Porter and Porter [34] and results obtained by Tsai et al. [44] in the absence of elastic plate.

4.3 Energy balance relation

The numerical values of |R| and |T| obtained by the present method are found to validate (see the last column of Table 2) the energy balance relation as given by

$$\begin{aligned} |R|^2 +~ \gamma ~ |T|^2 = 1, \end{aligned}$$
(51)

where \( \gamma =\displaystyle {\left( \frac{p_0 {\tilde{p}}_0}{k_{1,0}({\tilde{k}}_{1,0})}\right) \frac{ 2 p_0 {\hat{h}}_{1} + \sinh 2 p_0 {\hat{h}}_{1}}{2 k_{1,0}h_1 + \sinh 2 k_{1,0}h_1} \left( \frac{\cosh ^2 k_{1,0}h_1}{\cosh ^2 p_0 {\hat{h}}_{1}}\right) }. \)

This validation indicates that the numerical results obtained here are accurate.

Table 2 |R| and |T| versus \(K_1\) for \(N=20\) and different values of m
Full size table
Table 3 Comparison of the numerical values of |R| and |T| for different \(K_1.\)
Full size table

4.4 Effect of various system parameters

We have plotted |R| and |T| against \(k_{1,0}h_1\) in Fig. 7 for \(\theta =\pi /4\) to observe the effect of arbitrary bottom (in particular, symmetric parabolic hump here) as compared to flat bottom (\(H_j =1, j=0,1,2,\ldots 2m+1\)) in the presence of floating elastic plate. It is observed that more energy is reflected back due to the presence of parabolic hump, resulting in less energy to be transmitted towards lee side of floating elastic structure. As a consequence, floating structure as well as sea shore is protected, which accomplish the aim of this study.

Fig. 7
figure 7

|R| and |T| versus \(k_{1,0}h_1\) for flat bottom and parabolic bottom topography

Full size image

The effect of length of elastic plate \(({\hat{c}} -{\hat{b}})\) on |R| and |T| versus \(k_{1,0}h_1\) is investigated in Fig. 8. Here, the values of \({\hat{c}} -{\hat{b}}= 1.0, 2.0, 3.0\) are taken to analyse the effect. From this figure, it is viewed that for long waves corresponding to small wave numbers \(k_{1,0}h_1\), the flow is uniform along the horizontal direction by which there is a small amount of wave reflection by the horizontal plate for long waves. This is due to the reason that the plate appears to be transparent to the incident waves implying almost zero reflection for long waves. That means |R| tends to zero and |T| approaches one as \(k_{1,0}h_1\) vanishes, which means that a major part of the wave energy for long waves is transmitted into the plate covered region. On the other hand, for shorter waves, i.e. larger values of \(k_{1,0}h_1\), |R| become almost one, which happens due to the fact that shorter waves confined near the free surface and almost reflected back by the floating structure. This phenomenon is also observed by Sahoo et al. [35]. Further, it is clear that as the value of plate length increases, the value of |R| increases, whereas |T| decreases for the same. This is due to the fact that longer the length of elastic plate produces more reflection hence less transmission.

Fig. 8
figure 8

|R| and |T| versus \(k_{1,0}h_1\) for various values of length of elastic plate \({\hat{c}} -{\hat{b}} =1.0, 2.0, 3.0\) and fixed value of \(\theta = 20^{o}\)

Full size image

|R| and |T| versus \(k_{1,0}h_1\) for various values of the gap between bottom topography and elastic plate \(({\hat{b}} -{\hat{l}} = 0.5, 0.7, 0.9)\) are plotted in Fig. 9. It is observed that as the gap between plate and hump type bottom topography increases, the behaviour of |R| and |T| versus \(k_{1,0}h_1\) is same as mentioned in Fig. 8.

Fig. 9
figure 9

|R| and |T| versus \(k_{1,0}h_1\) for various values of gap \({\hat{b}} -{\hat{l}} =0.5,0.7, 0.9\) between the hump and elastic plate and fixed value of \(\theta = 30^{o}\)

Full size image

The effect of water depth \(H_m =H_{m+1}\) on |R| and |T| as a function of incident wave number \(k_{1,0}h_1\) is examined in Fig. 10. It is noticed that for lower values of depth (i.e. higher the hump height) \(H_m=H_{m+1}= 0.5\) as compared to \(H_m=H_{m+1}=0.6, 0.7\) produces more reflection, consequently, less transmission for the same which is obvious due to the behaviour of the physical problem.

Fig. 10
figure 10

|R| and |T| versus \(k_{1,0}h_1\) for various values of depth \(H_m=H_{m+1} =0.5, 0.6, 0.7 \) of water and fixed value of \(\theta = 20^{o}\)

Full size image

The effect of angle of incidence (\(\theta \)) on |R| and |T| as a function of incident wave number \(k_{1,0}h_1\) is shown in Fig. 11. Here the values of \(\theta =10^{o}, 20^{o}, 40^{o}, 55^{o}\) and \(70^{o}\) are considered. It is observed that for lower values of angle of incidence, less reflection occurs as compared to higher values of angles of incidence. Moreover, more energy is reflected back as the angle of incidence is increased; consequently, less energy will be transmitted to the lee side of the structure.

Fig. 11
figure 11

Effect of angle of incidence (\(\theta \)) on |R| and |T| versus \(k_{1,0}h_1\)

Full size image

The variation in |R| and |T| as a function of \(k_{1,0}h_1\) for various values of flexural rigidity \((D/h_1^{4} = 10, 10^2, 10^4)\) is plotted in Fig. 12. From this figure, it is observed that as the value of \(D/h_1^4\) increases |R| increases whereas |T| decreases for the same. This is due to the reason that for higher values of flexural rigidity, elastic plate becomes more rigid; hence, most of the waves which concentrate near the free surface are reflected back, and in the process, less incident wave energy is transmitted below the plate.

Fig. 12
figure 12

Effect of flexural rigidity \(D/h_1^{4}\) on |R| and |T| versus \(k_{1,0}h_1\)

Full size image

In Fig. 13, the plate deflection (\(\Re (\eta _{2m+1})\)) as a function of \(x/h_1\) is plotted for various values of flexural rigidity \((D/h_1^{4} = 10, 10^2, 10^3)\). From the figure, it is observed that the plate deflection is less for higher values of the flexural rigidity due to the fact that higher the flexural rigidity implying more rigidity of the plate which does not deform very much.

Fig. 13
figure 13

Variation of dimensionless plate deflection \(\Re (\eta _{2m+1})\) for various values of \(D/h_1^4\) and fixed value of \(k_{1,0}h_1=1.0,~ \theta =40^{o}\)

Full size image

In Fig. 14, the plate deflection (\(\Re (\eta _{2m+1})\)) as a function of \(x/h_1\) is plotted for various values of water depth \(H_m =H_{m+1}\). From the figure, it is observed that the plate deflection is less for lower values of depth (i.e. higher the hump height) \(H_m=H_{m+1}= 0.5\) as compared to \(H_m=H_{m+1}=0.6, 0.7\), which is due to the fact that higher the value of hump height produces more reflection and deflection of the plate decreases for the same.

Fig. 14
figure 14

Variation of dimensionless plate deflection \(\Re (\eta _{2m+1})\) for various values of \(H_m=H_{m+1}\) and fixed value of \(k_{1,0}h_1=1.0, ~\theta =40^{o}\)

Full size image

In Fig. 15, the effect of angle of incidence (\(\theta \)) on the plate deflection (\(\Re (\eta _{2m+1})\)) is depicted. Here, the values of \(\theta = 30^{o}, 50^{o}\) and \(70^{o}\) are taken to analyse the effect. From this figure, it is clear that with respect to the angle of incidence, the deflection of the plate decreases is due to the fact that for higher values of angle of incidence, more energy is reflected back and hence less transmission to lee side; consequently, less deflection is experienced by the elastic plate.

Fig. 15
figure 15

Variation of dimensionless plate deflection \(\Re (\eta _{2m+1})\) for various values of \(\theta \) and fixed value of \(k_{1,0}h_1=1.0\)

Full size image

Figure 16 shows the variation of strain (\(S_t\)) along the plate length for different values of rigidity of plate. It is observed that the strain is zero at the edges of the elastic plate which is in agreement with the assumption of free edge conditions of the floating structure. Further, it is observed that strain decreases as the flexural rigidity of the plate increases. Also, it is noticed that near the edges of the plate, strain increases very rapidly because the local effect of the evanescent modes is dominating near the edges.

The effect of plate rigidity on shear force \((S_f)\) is shown in Fig. 17. It is noticed that at the edges of the floating plate shear force is zero as assumed in the present study which reflects the accuracy of the computational results. Also, this figure shows that as the rigidity of the plate increases, the less shear force is experienced by the elastic plate.

Fig. 16
figure 16

Effect of flexural rigidity on strain (\(S_t\)) for fixed value of \(k_{1,0}h_1=0.2, ~\theta =0^{o}\)

Full size image
Fig. 17
figure 17

Effect of flexural rigidity on shear force (\(S_f\)) for fixed value of \(k_{1,0}h_1=0.2, ~\theta =0^{o}\)

Full size image

5 Conclusion

In this paper, the problem involving the transformation of incident wave energy by floating elastic structure, which is situated at a finite distance from an arbitrary bottom topography, is investigated. The method of step approximation along with matched eigenfunction expansion is utilized to solve the mixed boundary value problem. The present results have been validated with (i) Kaur et al. [17] and Linton [24] for the case of rigid floating structure over uniform flat bottom (ii) Hermans [13] in case of elastic plate over uniform flat bottom and (iii) Porter and Porter [34] and Tsai et al. [44] in case of undulated bottom. The effects of (i) length of plate, (ii) angle of incidence, (iii) water depth and (iv) distance between bottom topography and the elastic plate on reflection and transmission coefficients are analysed through various graphs. It has been observed that longer the length of elastic plate produces more reflection hence less transmission. Also, it is noticed that the lower values of depth (i.e. higher the hump height) help to produce more reflection; consequently, less transmission for the same is due to the behaviour of the physical problem. Moreover, more energy is reflected back as the angle of incidence is increased; consequently, less energy will be transmitted to the lee side of the structure. Also, for the higher values of flexural rigidity, plate becomes more rigid and it reflects more energy back and consequently less transmission to beach side. Furthermore, the effect of (i) flexural rigidity of elastic plate, (ii) hump height, (iii) and angle of incidence on plate deflection is analysed through graphs. The results show that for higher values of plate rigidity, plate becomes more rigid; hence, the deflection of plate decreases. Also, higher the value of hump height produces more reflection and hence less deflection of the plate is observed. Also, the effect of flexural rigidity on strain and shear force is analysed. It has been observed that strain decreases as the flexural rigidity of the plate increases. Moreover, near the edges of the plate, strain increases very rapidly due to the local effect of the evanescent modes near the edges. The energy balance relation is verified, which helps for ensuring the correctness of the numerical results of unknowns, namely reflection and transmission coefficients. This problem will give useful information to create the desirable tranquility zone near the seashore.