Keywords

1 Introduction

Submerged porous structures are frequently used as a breakwater to control the wave attack on gently sloping beaches, ports and harbours. Practical problems arising day-to-day life has motivated to investigate the wave interaction with submerged porous structures considering different conditions. Porous structures are not only constructed for controlling the tremendous wave power generated due to wave propagation but also essential in the attenuation of wave height and protection of coastal structures. Tremendous wave attack causes coastal erosion and creates a disturbance to the artificial and man-made structures. Submerged porous structures are one of the solutions to mitigate the coastal-related problems from high wave trains with less maintenance and long life period. Wave reflection from the structures plays a predominant role in the prediction of wave climate in harbours and wharfs. The significance of the submerged porous structures is studied by numerous researchers using numerical and experimental models. Numerical models are developed based on linear wave theory to investigate the submerged porous structure kept in various conditions with various key role parameters like porosity, friction, inertia, width of the porous structure and angle of wave attack. Sollitt and Cross [15] performed an elaborated study on the rectangular porous structure for finding the reflection and transmission coefficients in the presence of evanescent waves. Eigenfunction expansion method is used to relate the velocity potentials for finding the unknowns. Finally, the theoretical values are compared and validated with numerical values. Dattatri et al. [7] analysed the behaviour of the vertical, rectangular and trapezoidal submerged permeable and impermeable breakwaters with experimental study. The wave reflection due to the presence of vertical permeable porous structure is presented in Madsen [12] for shallow water waves. The detail derivation for the wave absorption due to the vertical homogeneous porous structure under the action of shallow water waves is performed. Further, Sulisz [17] examined a rubble-mound breakwater kept in infinite water depth and the reflection and transmission characteristics for the multi-layered breakwater of arbitrary cross section is analysed using boundary element method. The numerical method was validated with Sollitt and Cross [16] for the rectangular porous structure. Dalrymple et al. [2] used the eigenfunction expansion method to examine the submerged rectangular porous structure and porous structure backed by a rigid wall existing in the finite depth. The numerical study was performed for the plane wave and long wave approximation. An extensive numerical study has been performed on the wave absorption by rectangle porous barrier. The performance of the seawall protected by a submerged porous bar was examined by Reddy and Neelamani [14]. The wave force reduction on the caisson type breakwater due to the presence of submerged structure was investigated experimentally. Chen et al. [1] presented the numerical solution for submerged porous structure with seawall using time-dependent mild-slope approximation.

A detailed comparison of the existing analytical model and the developed numerical approach was performed and presented on the effect of geometric configuration and permeability properties of the porous structure on the wave reflection. The reflection and transmission characteristics of two submerged horizontal plates were examined by Liu et al. [11]. Liu and Luo [10] developed a numerical model to examine the two submerged breakwater using long wave approximation. The variation in the width of the breakwater and depth of the two submerged breakwaters are analysed. Das and Bora [3] examined the damping of an elevated porous structure away from impermeable wall and the numerical model is developed for submerged porous structure near to the impermeable wall and far away from the impermeable wall. The matched eigenfunction expansion method is utilized for finding the reflection characteristics of the porous structure and rigid wall. The study was extended for the vertical porous structure placed on elevated bottom and multiple submerged structures by Das and Bora [4,5,6]. The study on the wave trapping by submerged porous structure is well examined by the researchers for the attenuation of wave height. The generalized solution for the submerged multi-layer horizontal porous plates was examined analytically and experimentally by Fang et al. [8] using matched eigenfunction expansion method. An effective practical designing criterion was developed due to the effect of porosity, width and number of plates.

Zhao et al. [18] developed a numerical model for the vertical impermeable wall protected with submerged porous bar. The partial reflection from the impermeable wall is computed and compared with BEM solution and experimental data. Further, Zhao et al. [19] extended the study for analysing the multiple porous bars in the presence of end wall. Recently, Zhao et al. [20] examined the oblique wave scattering by submerged porous structure supported with seawall. The eigenfunction expansion method and multi-domain BEM approach are used to examine the wave behaviour.

In the present study, a numerical model is developed for the wave interaction with single and multiple submerged porous structures with impermeable wall. The study demonstrates the wave reflection, transmission, wave forces and energy loss due to porous structures in finite water depth. The eigenfunction expansion method and continuity of velocity and pressure are used to analyse the effectiveness of the submerged porous structure.

2 Mathematical Formulation

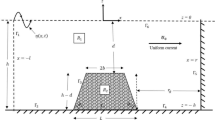
The wave absorption due to the presence of the submerged porous structure is analysed in the presence of impermeable wall under the assumption of linearized wave theory. The study is performed considering single porous structure in the presence of wall Fig. 1a and two porous structures in the presence of end wall (Fig. 1b). The monochromatic wave is incident along the positive x-direction. A two-dimensional coordinate system is considered in the analysis with x-axis being the horizontal and the z-axis considered vertically downward negative. The fluid domain in Fig 1a is divided into three regions, upstream open water region at \( - \infty < x < 0,\; - h < z < 0 \) as region 1, the porous structure region at \( 0 < x < U,\; - h < z < 0 \) as region 2 and downstream domain at \( U < x < U + L,\; - h < z < 0 \) as region 3.

Fig. 1
figure 1

a Submerged porous structure and b two porous structures with impermeable wall

Full size image

In Fig. 1b, two submerged porous structures of width u and w are placed at a distance L from the end wall. The distance between the porous structures is considered to be V. Assuming that the wave elevation is simple harmonic in time with frequency \( \omega \), the velocity potential \( \Phi _{i} \left( {x,y,z,t} \right) \) and the surface deflection \( \zeta_{i} \left( {x,t} \right) \) can be written as \( \Phi _{i} \left( {x,y,z,t} \right) = {\mathrm{Re}}\left\{ {\phi_{i} \left( {x,z} \right)} \right\}e^{{ - i\left( {\lambda y - \omega t} \right)}} \) and \( \zeta_{i} \left( {x,t} \right) = Re\left\{ {\eta_{i} \left( x \right)} \right\}e^{i\omega t} \) where \( Re \) denotes the real part with \( \lambda = k_{0} \sin \theta \) represents the progressive wave mode, \( \theta \) is the angle of incidence and \( k_{0} \) is the progressive wave number. The spatial velocity potential, \( \phi_{i} (x,y,z) \), satisfies the Helmholtz equation given by

$$ \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{\partial^{2} \phi_{i} }}{{\partial z^{2} }} - \lambda^{2} \phi_{i} = 0\quad {\mathrm{for}}\quad - h \le z \le 0. $$
(1)

The linearized free surface boundary condition in each of the regions is given by

$$ \frac{{\partial \phi_{i} }}{\partial z} - \frac{{\Gamma _{i} }}{h}\phi_{i} = 0\quad {\mathrm{at}}\quad z = 0, \; i = 1,2,3 \ldots $$
(2)

where \( \Gamma _{1} =\Gamma _{3} =\Gamma _{5} = \frac{{\omega^{2} h}}{g} \) and \( \Gamma _{2} =\Gamma _{4} = \frac{{\omega^{2} h(s + if)}}{g}. \)

The bottom boundary condition is given by

$$ \frac{{\partial \phi_{i} }}{\partial z} = 0\,\,{\mathrm{at}}\,\,z = - h. $$
(3)

In the free surface and the porous structure region, the progressive wave number satisfies the dispersion relation of the form

$$ \omega^{2} = gk_{0} \tan hk_{0} h, = - gk_{n} \tan \,k_{n} h\quad \quad n = 1,2,3 \ldots $$
(4)
$$ \omega^{2} h(s + if) = gp_{0} h\tan h p_{0} h = - gp_{n} h\tan p_{n} h\quad \quad n = 1,2,3 \ldots $$
(5)

where g is acceleration due to gravity, k0 is progressive wave number, kn is evanescent wave numbers in open water region, h is water depth, p0 is progressive wave number pn is evanescent wave numbers in porous structure region, f is linear friction factor, s is inertial term, i is imaginary number and \( \omega \) is wave frequency. The dispersion relation for the open water region is solved with Newton–Raphson method and for the porous structure region perturbation method [13]. The effect of inertia and friction is considered in the dispersion relation for calculating the imaginary wave number in the porous water region. In the present study, porosity is considered as 40% and friction factor is considered as 0.25 [2, 3, 15]. The inertia force is given by the following equation:

$$ s = 1 + A_{m} \left[ {\frac{1 - e}{e}} \right], $$
(6)

where s is inertia, e is porosity and Am is added mass due to wave propagation. The inertial effect, s is considered as unity [15, 16] and the friction factor is considered to be 0.25 [3, 4]. The porous structures are immovable which suggests that the porous structures are in static condition and the added mass is considered negligible.

3 Method of Solution

The numerical model is developed in order to analyse the submerged porous structure in the presence of rigid wall. The wave reflection coefficient, transmission coefficient and energy loss from the porous structure are analysed using the eigenfunction expansion method.

3.1 Single Porous Structure with End Wall

The velocity potentials \( \phi_{i} \left( {x,y} \right) \) for \( i = 1,\,2,\,3 \) satisfies the governing Eq. (1) along with the boundary condition (2) and (3) as defined in Sect. 2. The velocity potentials \( \phi_{i} \left( {x,y} \right) \) for \( i = 1,\,2,\,3 \) are of the form

$$ \begin{aligned}\phi_{1} &= \left\{ {e^{{i\sqrt {(k_{0}^{2} - \lambda^{2} )} x}} + R_{0} e^{{ - i\sqrt {(k_{0}^{2} - \lambda^{2} )} x}} } \right\}I_{0} (z) + \sum\limits_{n = 1}^{\infty } {R_{n} } e^{{ - i\sqrt {(k_{n}^{2} - \lambda^{2} )} x}} I_{n} (z), \\ & {\mathrm{at }}\, - \infty \le x \le 0 \end{aligned}$$
(7)
$$ \phi_{2} = \sum\limits_{n = 0}^{\infty } {\left\{ {A_{n} e^{{i\sqrt {(p_{n}^{2} - \lambda^{2} )} x}} + B_{n} e^{{ - i\sqrt {(p_{n}^{2} - \lambda^{2} )} (x - U)}} } \right\}} P_{n} (z),\quad \,\,{\mathrm{at }}\, 0\le x \le U $$
(8)
$$ \phi_{3} = \sum\limits_{n = 0}^{\infty } {\left\{ {T_{n} e^{{i\sqrt {(p_{n}^{2} - \lambda^{2} )} (x - U)}} + D_{n} e^{{ - i\sqrt {(p_{n}^{2} - \lambda^{2} )} (x - U - L)}} } \right\}} I_{n} (z),\quad {\mathrm{at \, \, U}} \le x \le U + L, $$
(9)

where \( R_{n} ,n = 0,1,2 \ldots ,A_{n} ,B_{n} ,n = 0,1,2, \ldots . \) and \( T_{n} ,D_{n} ,n = 0,1,2, \ldots . \) are the unknown constants to be determined. The eigenfunctions \( I_{n} \left( z \right)\,{\mathrm{for}}\,n = 0,1,2, \ldots \) and \( P_{n} \left( z \right)\;{\mathrm{for}}\;n = 0,1,2, \ldots \) given by

$$ I_{n} \left( z \right) = \frac{ig}{\omega }\frac{{\cosh k_{n} \left( {h + z} \right)}}{{\cosh k_{n} h}}\,{\mathrm{for}}\,n = 0\,{\mathrm{and}}\,I_{n} \left( z \right) = \frac{ig}{\omega }\frac{{\cos k_{n} \left( {h + z} \right)}}{{\cos k_{n} h}}\,{\mathrm{for}}\,n = 1,2, \ldots $$
(10a)
$$ P_{n} (z) = \frac{ig}{\omega }\frac{{\cosh p_{n} \left( {h + z} \right)}}{{\cosh p_{n} h}}\;{\mathrm{for}}\;n = 0\;{\mathrm{and}}\;P_{n} (z) = \frac{ig}{\omega }\frac{{\cos p_{n} \left( {h + z} \right)}}{{\cos p_{n} h}}\,{\mathrm{for}}\,n = 1,2, \ldots , $$
(10b)

where \( k_{n} \, {\mathrm{ and }} \, p_{n} \;{\mathrm{for}}\,n = 0,1,2, \ldots \) are the eigenvalues. These eigenvalues satisfy the dispersion relation as defined in Eqs. (4) and (5). It may be noted that the eigenfunctions \( I_{n} \left( z \right) \)’s and \( P_{n} \left( z \right) \)’s satisfy the orthogonality relation as given by

$$ \left\langle {I_{m} ,I_{n} } \right\rangle_{j = 1,3} = \left\{ {\begin{array}{*{20}l} 0 \hfill & {\mathrm{for}} \hfill & {m \ne n,} \hfill \\ {C^{\prime}_{n} } \hfill & {\mathrm{for}} \hfill & {m \ne n,} \hfill \\ \end{array} } \right.\;{\mathrm{and}}\;\left\langle {P_{m} ,P_{n} } \right\rangle = \left\{ {\begin{array}{*{20}l} 0 \hfill & {\mathrm{for}} \hfill & {m \ne n,} \hfill \\ {C_{n}^{{\prime \prime }} } \hfill & {\mathrm{for}} \hfill & {m \ne n,} \hfill \\ \end{array} } \right. $$

with respect to the orthogonal mode-coupling relation defined by

$$ \left\langle {I_{m} I_{n} } \right\rangle = \int\limits_{ - h}^{0} {I_{m} (z)I_{n} } (z)dz\;{\mathrm{and}}\;\left\langle {P_{m} ,P_{n} } \right\rangle = \int\limits_{ - h}^{0} {P_{m} (z)P_{n} } (z)dz, $$

where \( C^{\prime}_{n} = \left\{ {\frac{{ - g^{2} }}{{\omega^{2} }}} \right\}\left\{ {\frac{{2k_{n} h + \sinh 2k_{n} h}}{{4k_{n} \cosh^{2} k_{n} h}}} \right\} \) and \( C^{\prime\prime}_{n} = \left\{ {\frac{{ - g^{2} }}{{\omega^{2} }}} \right\}\left\{ {\frac{{2p_{n} h + \sinh 2p_{n} h}}{{4p_{n} \cosh^{2} p_{n} h}}} \right\}. \)

The continuity of velocity and pressure at the interface \( x = 0 \) and \( x = U \), \( - h < z < 0\) is given by

$$ \phi_{1x} = e\phi_{2x} \;{\mathrm{and}}\;\phi_{1} = G\phi_{2} \;{\mathrm{at}}\;x = 0,\quad e\phi_{2x} = \phi_{3x} \;{\mathrm{and}}\;G\phi_{2} = \phi_{3} \;{\mathrm{at}}\;x = U, $$
(11a)

The wall condition is adopted for obtaining the full wave reflection [9]:

$$ \phi_{3x} = \mu k_{0} \phi_{3} , { }\mu = i\frac{{1 - K_{w} }}{{1 + K_{w} }} \, {\mathrm{ at }} \, x = b + L, \, $$
(11b)

Using the progressive wave mode, the solution for the boundary value problem considering the matching conditions and orthogonal mode-coupling relation for submerged porous structure with end wall is obtained as

$$ K_{R} = \frac{{i(1 - m^{2} )\sin \left\{ {b\sqrt {\left( {p_{0}^{2} - \lambda^{2} } \right)} } \right\}}}{{2m\,\cos \left\{ {b\sqrt {\left( {p_{0}^{2} - \lambda^{2} } \right)} } \right\} + i(1 + m^{2} )\sin \left\{ {b\sqrt {\left( {p_{0}^{2} - \lambda^{2} } \right)} } \right\}}}, $$
(12)
$$ K_{T} = \frac{{2me^{{ - ib(p_{0}^{2} - \lambda^{2} )^{1/2}}} }}{{\left[ {e^{{iL\sqrt {(k_{0}^{2} - \lambda^{2} )} }} } \right]2m\,\cos \left\{ {b\sqrt {\left( {p_{0}^{2} - \lambda^{2} } \right)} } \right\} + i(1 + m^{2} )\sin \left\{ {b\sqrt {\left( {p_{0}^{2} - \lambda^{2} } \right)} } \right\}}}. $$
(13)

Considering both progressive and evanescent wave mode, the solution for the boundary value problem considering the matching conditions and orthogonal mode-coupling relation for submerged porous structure with end wall is obtained as

$$ \begin{aligned} & \left\{ {1 - R_{0} } \right\}\int\limits_{ - h}^{0} {I_{0} (z)I_{n} (z)dz - \sum\limits_{i = 0}^{N} {\sqrt {\left( {\frac{{k_{n}^{2} - \lambda^{2} }}{{k_{0}^{2} - \lambda^{2} }}} \right)} } R_{n} } \int\limits_{ - h}^{0} {I_{m} (z)I_{n} (z)dz} \\ & = e\left[ {\sum\limits_{n = 0}^{N} {\sqrt {\left( {\frac{{p_{n}^{2} - \lambda^{2} }}{{k_{0}^{2} - \lambda^{2} }}} \right)} } \left( {A_{n} - B_{n} U_{n} } \right)\int\limits_{ - h}^{0} {P_{n} (z)I_{n} (z)dz} } \right], \\ \end{aligned} $$
(14)
$$ \begin{aligned} \left\{ {1 + R_{0} } \right\}\int\limits_{ - h}^{0} {I_{0} (z)I_{n} (z)dz + \sum\limits_{i = 0}^{N} {R_{n} } } \int\limits_{ - h}^{0} {I_{m} (z)I_{n} (z)dz} \\ = G\left[ {\sum\limits_{i = 0}^{N} {\left( {A_{n} + B_{n} U_{n} } \right)} \int\limits_{ - h}^{0} {P_{n} (z)I_{n} (z)dz} } \right] ,\\ \end{aligned} $$
(15)
$$\begin{aligned} e\left[ {\sum\limits_{i = 0}^{N} {\left( {A_{n} U_{n} - B_{n} } \right)} \int\limits_{ - h}^{0} {P_{n} (z)I_{n} (z)dz} } \right] & = \sum\limits_{i = 0}^{N} {\sqrt {\left( {\frac{{k_{n}^{2} - \lambda^{2} }}{{p_{0}^{2} - \lambda^{2} }}} \right)} \left( {T_{n} - D_{n} L_{n} } \right)} \\ &\int\limits_{ - h}^{0} {I_{n} (z)I_{n} (z)dz} ,\\ \end{aligned} $$
(16)
$$ G\left[ {\sum\limits_{i = 0}^{N} {\left( {A_{n} U_{n} + B_{n} } \right)} \int\limits_{ - h}^{0} {P_{n} (z)I_{n} (z)dz} } \right] = \sum\limits_{i = 0}^{N} {\left( {T_{n} + D_{n} L_{n} } \right)} \int\limits_{ - h}^{0} {I_{n} (z)I_{n} (z)dz} , $$
(17)
$$ \begin{aligned} \sum\limits_{i = 0}^{N} {\left( {i\mu k_{0} + \sqrt {k_{n}^{2} - \lambda^{2} } } \right)} L_{n} T_{n} \int\limits_{ - h}^{0} {I_{n} (z)^{2} dz} & + \sum\limits_{i = 0}^{N} {\left( {i\mu k_{0} - \sqrt {k_{n}^{2} - \lambda^{2} } } \right)} D_{n} \\ & \int\limits_{ - h}^{0} {I_{n} (z)^{2} dz} = 0, \\ \end{aligned} $$
(18)

where \( U_{n} = \exp \left\{ {iU\sqrt {(k_{n}^{2} - \lambda^{2} )} } \right\}, \) \( V_{n} = \exp \left\{ {iV\sqrt {(k_{n}^{2} - \lambda^{2} )} } \right\}, \) \( L_{n} = \exp \left\{ {iL\sqrt {(k_{n}^{2} - \lambda^{2} )} } \right\}, \) \( m = \frac{e}{s + if}\sqrt {\left( {\frac{{p_{0}^{2} - \lambda^{2} }}{{k_{0}^{2} - \lambda^{2} }}} \right)} ,\;G = s + if\;{\mathrm{and}}\;\int\limits_{ - h}^{0} {P_{n} (z)I_{n} (z)dz)} = \frac{g(s + if - 1)}{{\left( {p_{n}^{2} - k_{n}^{2} } \right)}}. \)

The infinite series sums of the algebraic equations as presented in (14)–(18) are obtained and the solution is obtained for the system of \( \left( {5N + 5} \right) \) equations. The velocity potentials in each of the three regions consist of \( \left( {5N + 5} \right) \) unknown coefficients such as \( R_{n} ,T_{n} ,n = 0,1,2, \ldots ,\,N, \) \( A_{n} ,B_{n} ,D_{n} ,n = 0,1,2 \ldots ,\,N. \) The full solution is obtained by solving the system of linear equations in terms of wave reflection and transmission coefficients as

$$ \, K_{R} = \left| {R_{0} } \right|\,{\mathrm{ and }}\,K_{T} = \left| {T_{0} } \right|, $$
(19a)
$$ {\mathrm{Energy}}\;{\mathrm{loss }} = \, 1 - (K_{R}^{2} + K_{T}^{2} ). $$
(19b)

3.2 Multiple Porous Structure with End Wall

In the case of two porous structures in the presence of end wall, the velocity potentials \( \phi_{i} \left( {x,y} \right) \) for \( i = 1,2,3,4,5 \) satisfies the governing Eq. (1) along with the boundary condition (2) and (3) as defined in Sect. 2. The velocity potentials \( \phi_{i} \left( {x,y} \right) \) for \( i = 1,2,3,4,5 \) are of the form

$$ \begin{aligned} \phi_{1} &= \left\{ {e^{{i\sqrt {(k_{0}^{2} - \lambda^{2} )x} }} + R_{0} e^{{ - i\sqrt {(k_{0}^{2} - \lambda^{2} )} x}} } \right\}I_{0} (z) \\ & \quad + \sum\limits_{n = 1}^{\infty } {R_{n} } e^{{ - i\sqrt {(k_{n}^{2} - \lambda^{2} )x} }} I_{n} (z), \quad {\mathrm{at}}\; \, { - }\infty \le x \le 0 \end{aligned}$$
(20)
$$ \phi_{2} = \sum\limits_{n = 0}^{\infty } {\left\{ {A_{n} e^{{i\sqrt {(p_{n}^{2} - \lambda^{2} )} x}} + B_{n} e^{{ - i\sqrt {(p_{n}^{2} - \lambda^{2} )} (x - u)}} } \right\}} P_{n} (z),\;{\mathrm{at}}\; 0\le x \le u, $$
(21)
$$ \phi_{3} = \sum\limits_{n = 0}^{\infty } {\left\{ {C_{n} e^{{i\sqrt {(k_{n}^{2} - \lambda^{2} )} (x - u)}} + D_{n} e^{{ - i\sqrt {(k_{n}^{2} - \lambda^{2} )(x - V^{1} )} }} } \right\}} I_{n} (z),\;{\mathrm{at}}\;{\mathrm{u}} \le x \le V^{1} , $$
(22)
$$ \phi_{4} = \sum\limits_{n = 0}^{\infty } {\left\{ {E_{n} e^{{i\sqrt {(p_{n}^{2} - \lambda^{2} )(x - V^{1} )} }} + F_{n} e^{{ - i\sqrt {(p_{n}^{2} - \lambda^{2} )} (x - W^{1} )}} } \right\}} P_{n} (z),\;{\mathrm{at}}\;V^{1} \le x \le W^{1} , $$
(23)
$$ \phi_{5} = \sum\limits_{n = 0}^{\infty } {\left\{ {T_{n} e^{{i\sqrt {(k_{n}^{2} - \lambda^{2} )} (x - W^{1} )}} + J_{n} e^{{ - i\sqrt {(k_{n}^{2} - \lambda^{2} )} (x - W^{1} - L)}} } \right\}} I_{n} \left( z \right) \quad {\mathrm{ at}}\; \, W^{1} \le x \le W^{1} + L. $$
(24)

where \( V^{1} = u + V \, {\mathrm{ and }} \, W^{1} = u + V + w. \)

The continuity of velocity and pressure at the interface \( x = 0, \) \( x = u, \) \( x = u + V \) and \( x = u + V + w \) at \( - h < z < 0 \) is given by

$$ \phi_{1x} = e\phi_{2x}\, {\mathrm{and }} \, \phi_{1} = G\phi_{2} \, {\mathrm{ at }} \, x = 0, \, \quad \quad e\phi_{2x} = \phi_{3x} \, {\mathrm{ and }} \, G\phi_{2} = \phi_{3} \, {\mathrm{ at }} \, x = u, \, $$
(25a)
$$ \phi_{3x} = e\phi_{4x} \;{\mathrm{and}}\;\phi_{3} = G\phi_{4} \;{\mathrm{at}}\; \, x = V^{1} ,\quad e\phi_{4x} = \phi_{5x} \;{\mathrm{and}}\;G\phi_{4} = \phi_{5} \, {\mathrm{ at }} \, x = W^{1} . \, $$
(25b)

Using the orthogonal mode-coupling relation and the continuity of velocity and pressure with wall condition, the unknowns for the submerged porous structure with end wall is determined. The system of equation is represented for \( n = 0,1,2, \ldots ,\,N, \) as

$$ \begin{aligned} & \left\{ {1 - R_{0} } \right\}\int\limits_{ - h}^{0} {I_{0} (z)I_{n} (z)dz - \sum\limits_{i = 0}^{N} {\sqrt {\left( {\frac{{k_{n}^{2} - \lambda^{2} }}{{k_{0}^{2} - \lambda^{2} }}} \right)} } R_{n} } \int\limits_{ - h}^{0} {I_{m} (z)I_{n} (z)dz} \\ & = e\left[ {\sum\limits_{n = 0}^{N} {\sqrt {\left( {\frac{{p_{n}^{2} - \lambda^{2} }}{{k_{0}^{2} - \lambda^{2} }}} \right)} } \left( {A_{n} - B_{n} u_{n} } \right)\int\limits_{ - h}^{0} {P_{n} (z)I_{n} (z)dz} } \right], \\ \end{aligned} $$
(26)
$$ \begin{aligned} & \left\{ {1 + R_{0} } \right\}\int\limits_{ - h}^{0} {I_{0} (z)I_{n} (z)dz + \sum\limits_{i = 0}^{N} {R_{n} } } \int\limits_{ - h}^{0} {I_{m} (z)I_{n} (z)dz} \\ & \quad\quad\quad\quad\quad\quad\quad= G\left[ {\sum\limits_{n = 0}^{N} {\left( {A_{n} + B_{n} u_{n} } \right)} \int\limits_{ - h}^{0} {P_{n} (z)I_{n} (z)dz} } \right], \end{aligned}$$
(27)
$$ \begin{aligned} & e\left[ {\sum\limits_{n = 0}^{\infty } {\sqrt {\left( {\frac{{p_{n}^{2} - \lambda^{2} }}{{p_{0}^{2} - \lambda^{2} }}} \right)} \left( {A_{n} u_{n} - B_{n} } \right)} \int\limits_{ - h}^{0} {P_{n} (z)I_{n} (z)dz} } \right] \\ & = \left[ {\sqrt {\left( {\frac{{k_{n}^{2} - \lambda^{2} }}{{p_{0}^{2} - \lambda^{2} }}} \right)} \left( {C_{n} - D_{n} V_{n} } \right)\int\limits_{ - h}^{0} {I_{n} (z)I_{n} (z)dz} } \right], \\ \end{aligned} $$
(28)
$$ G\left[ {\sum\limits_{n = 0}^{N} {\left( {A_{n} u_{n} + B_{n} } \right)} \int\limits_{ - h}^{0} {P_{n} (z)I_{n} (z)dz} } \right] = \left[ {\sum\limits_{i = 0}^{N} {(C_{n} + D_{n} V_{n} )} \int\limits_{ - h}^{0} {I_{n} (z)I_{n} (z)dz} } \right], $$
(29)
$$ \begin{aligned} & \left[ {\sum\limits_{i = 0}^{N} {\sqrt {\left( {\frac{{k_{n}^{2} - \lambda^{2} }}{{k_{0}^{2} - \lambda^{2} }}} \right)} } \left( {C_{n} V_{n} - D_{n} } \right)\int\limits_{ - h}^{0} {I_{n} (z)I_{n} (z)dz} } \right] \\ & = \left[ {\sum\limits_{n = 1}^{N} {\sqrt {\left( {\frac{{p_{n}^{2} - \lambda^{2} }}{{k_{0}^{2} - \lambda^{2} }}} \right)} \left( {E_{n} - F_{n} w_{n} } \right)} \int\limits_{ - h}^{0} {P_{n} (z)I_{n} (z)dz} } \right], \\ \end{aligned} $$
(30)
$$ \left[ {\sum\limits_{i = 0}^{N} {\left( {C_{n} V_{n} + D_{n} } \right)} \int\limits_{ - h}^{0} {I_{n} (z)I_{n} (z)dz} } \right] = G\left[ {\sum\limits_{n = 0}^{N} {\left( {E_{n} + F_{n} w_{n} } \right)} \int\limits_{ - h}^{0} {P_{n} (z)I_{n} (z)dz} } \right], $$
(31)
$$ \begin{aligned} e\left[ {\sum\limits_{n = 0}^{N} {\left( {E_{n} w_{n} - F_{n} } \right)} \int\limits_{ - h}^{0} {P_{n} (z)I_{n} (z)dz} } \right] & = \sum\limits_{i = 0}^{N} {\sqrt {\left( {\frac{{k_{n}^{2} - \lambda^{2} }}{{p_{n}^{2} - \lambda^{2} }}} \right)} (T_{n} - J_{n} } L_{n})\\ & \quad \int\limits_{ - h}^{0} {I_{n} (z)I_{n} (z)dz} , \end{aligned} $$
(32)
$$ G\left[ {\sum\limits_{n = 0}^{N} {\left( {E_{n} w_{n} + F_{n} } \right)} \int\limits_{ - h}^{0} {P_{n} (z)I_{n} (z)dz} } \right] = \sum\limits_{i = 0}^{N} {(T_{n} - J_{n} L_{n} )} \int\limits_{ - h}^{0} {I_{n} (z)I_{n} (z)dz} , $$
(33)
$$\begin{aligned} &\sum\limits_{i = 0}^{N} {\left( {i\mu k_{0} + \sqrt {k_{n}^{2} - \lambda^{2} } } \right)} L_{n} T_{n} \int\limits_{ - h}^{0} {I_{n} (z)^{2} dz} \\& \quad+ \sum\limits_{i = 0}^{N} {\left( {i\mu k_{0} - \sqrt {k_{n}^{2} - \lambda^{2} } } \right)} J_{n} \int\limits_{ - h}^{0} {I_{n} (z)^{2} dz} = 0, \end{aligned}$$
(34)

where \( I_{n} \left( z \right){\mathrm{ and }}P_{n} \left( z \right), \) are eigenfunctions in open and porous water regions, \( G = s + if, \) \( \int\limits_{ - h}^{0} {P_{n} (z)I_{n} (z)dz)} = \frac{g(s + if - 1)}{{p_{n}^{2} - k_{n}^{2} }}, \) \( u_{n} = \exp \left\{ {iu(p_{n}^{2} - \lambda^{2} )^{1/2} } \right\}, \) \( V_{n} = \exp \left\{ {iV(k_{n}^{2} - \lambda^{2} )^{1/2} } \right\}, \) \( w_{n} = \exp \left\{ {iw(p_{n}^{2} - \lambda^{2} )^{1/2} } \right\} \) and \( L_{n} = \exp \left\{ { - iL(k_{n}^{2} - \lambda^{2} )^{1/2} } \right\}. \)

The infinite series sums of the algebraic equations as presented in (26)–(34) are obtained and the solution is obtained for the system of \( \left( {9N + 9} \right) \) equations. The expansion formulae for each of the three regions consist of \( \left( {9N + 9} \right) \) unknown coefficients such as \( R_{n} ,T_{n} , \) \( n = 0,1,2, \ldots ,\,N, \) \( A_{n} ,B_{n} ,n = 0,1,2, \ldots ,N, \) \( C_{n} ,D_{n} ,n = 0,1,2, \ldots ,N, \) \( E_{n} ,F_{n} ,J_{n} ,n = 0,1,2, \ldots ,N. \) The full solution is obtained by solving the system of linear equations in terms of wave reflection and transmission coefficients as in Eq. (19a,19b).

4 Numerical Results and Discussions

The wave interaction with submerged porous structures are considered in two different conditions (i) submerged porous structure with end wall (ii) multiple submerged porous structures with end wall at a distance. Wave reflection, transmission, wave forces and energy loss from the porous structures are analysed and presented for both single and double porous barrier. Present study elaborates the importance of porosity, friction, angle of wave attack, width between the porous structures and non-dimensional width of the structure. The convergence in the wave reflection is observed with the increase in the evanescent wave modes N.

4.1 Submerged Porous Structure Supported with Seawall

Porous structure supported with sea wall is examined and the behaviour of the structure is analysed. Reflection coefficient depends upon porosity, angle of incidence, non-dimensional width of the porous structure and friction. Hence, in the first trial, the effect of angle of incidence is studied. Various values of angle of incidences 0°, 15°, 30°, 45° and 60° are considered and variation in reflection coefficient is studied. Maximum reflection is observed for lower values of angle of incidence and oscillation in reflection coefficient is observed for lower values of k0h. For higher values of angle of incidence, oscillation in reflection coefficient vanishes. The increase in the angle of incidence ϴ causes variation in transmission coefficient.

Energy loss from the porous structure is presented for various values of ϴ. Figure 2a demonstrates the variation of reflection coefficient versus k0h for U/h  = 0.5, f  = 0.25 and e  = 0.4 for various angles of wave incidence. In the case of k0h  = 3, variation in wave reflection is observed at an angle of incidence 0°. An 1.12% reduction in reflection coefficient is noticed at 15°, 4.93% reduction at 30°, 13.078% reduction at 45° and 30.28% reduction at 60° angle of incidence. Figure 2b demonstrates the minimum variation in transmission coefficients for various values of angle of attack. Variation in angle of incidence causes minimum variation in energy absorption due to the sufficient width of the porous structure. In Fig. 2c, the variation in energy loss against k0h for various angle of incidences is presented, and Fig. 2d demonstrates the variation in wave forces against k0h. Increase in angle of incidence shows considerable variations in the wave forces. For angle of incidence 0° and 15°, a similar trend is noticed. For angle of incidences 30°, 45° and 60°, the trend of the wave forces is different compared with 0° and 15°.

Fig. 2
figure 2

Effect of angle of incidence on a reflection coefficient, b transmission coefficient, c energy loss and d wave forces for U/h = 0.5, f  = 0.25 and e = 0.4

Full size image

If the adopted porosity is unity, then the transmission coefficient is one KT = 1, which causes complete reflection at D0 = 1 [3] and complete reflection is observed due to end wall at x  = 0. Due to total reflection from end wall, for minimum k0h values, maximum transmission (KT = 1) and maximum reflection (KR= 1) due to end wall at x  = 0 are observed.

4.2 Two Submerged Porous Structures with Seawall

In the present section, the discussion on wave interaction with two submerged porous structures is presented. Variation in wave reflection characteristics, transmission characteristics and energy loss are studied for various non-dimensional width of the porous structure.

In Fig. 3a, for \( U/h \, = \, 0.5, \) maximum wave reflection is observed at \( k_{0} h \, = \, 2.5, \) and again for \( U/h \, = \, 0.125, \) maximum reflection coefficient is observed at \( k_{0} h \, = \, 5.5. \) Comparison between the \( U/h \, = \, 0.125 \, \) and 0.5 is that \( U/h \, = \, 0.5 \) is able to reflect the long waves and \( U/h \, = \, 0.125 \) is able to reflect the moderate waves. Figure 3b presents the wave reflection from the second porous structure. Minimum wave reflection is observed at \( 6 < k_{0} h < 7 \) from the first porous structure and maximum wave reflection is observed at \( k_{0} h \ge 7 \) from the second porous structure. Hence, the maximum transmission from the first porous structure is reflected from the second porous structure. Falling trend in wave transmission Fig. 3c is observed in the presence of two submerged porous structures with end wall for all \( U/h \). Increase in width of the porous structure causes a decrease in wave transmission and an increase in energy loss. The oscillations in wave reflection and transmission vanish with the increase in width of the porous structure.

Fig. 3
figure 3

Effect of non-dimensional width of the structure on reflection from a structure 1 and b structure 2, c transmission coefficient and d energy loss for \( f = 0.25 \), \( s = 1 \), \( e = 0.4 \) and ϴ = 0°

Full size image

5 Conclusions

In the present study, the importance of submerged porous structures on wave reflection, transmission, energy loss and wave forces is studied. The study is performed considering (a) single porous structure and (b) two porous structures in the presence of end wall. The monochromatic wave is incident on along the positive x-direction. The matched eigenfunction expansion method is adopted to solve the boundary value problem.

  • In the first case, the submerged porous structure with end wall is examined. Porosity is considered as 0.4, friction factor is considered as 0.25 and angle of wave attack is varied from 0° to 60°.

  • Oscillations are observed in reflection coefficient for lower values of angle of wave attack. Wave reflection is maximum for lower angle of wave attack and minimum for higher angle of wave attack.

  • Maximum wave reflection is observed at ϴ  = 0°, 30% reduction in reflection coefficient is observed at ϴ  = 60° compared with ϴ  = 0°. Very less variation in transmission coefficients is noticed for various values of angle of attack.

  • In the second case, the width of the submerged porous structure modelled in the first condition is divided into two porous structures. Similar relations are observed in reflection characteristics, transmission characteristics and energy loss.

  • The width of the submerged porous structure is varied from \( U/h \, = \, 0.125 - 0.5. \) Maximum reflection coefficient from the structure for all values of \( U/h \) is 0.74 but an increase in width of the porous structure is able to reflect the long waves. From Fig. 3a for \( U/h \, = \, 0.5, \) maximum wave reflection is observed at \( k_{0} h \, = \, 2.5, \) similarly for \( U/h \, = \, 0.125, \) maximum reflection coefficient is observed at \( k_{0} h \, = \, 5.5. \)

  • The advantage of the two porous structures is that the transmitted wave from the first porous structure is reflected by the second porous structure.