Numerical Study on the Influence of Head Wave on the Hydrodynamic Derivatives of a Container Ship

Abstract

Traditionally, ship maneuvering performances are predicted in calm water condition to evaluate the directional stability and turning ability of the ship in the early design stages. Evaluation of maneuvering performance of a ship including wave effect is more realistic and important for the safety of ships at sea. Determination of hydrodynamic derivatives is the basic step in solving maneuvering equations of motion. Accurate estimation of hydrodynamic derivatives is necessary for the prediction of vessel trajectories. As the ship maneuvers through seaway, the effect of wave load will alter the maneuvering derivatives, consequently the vessel trajectory will be affected significantly. Hence, the influence of wave on hydrodynamic derivatives needs to be determined. For the present study, horizontal planar motion mechanism tests are numerically simulated for a container ship in head sea condition using RANS-based CFD solver. Obtained force/moment time series include both wave excitation forces/moment and hydrodynamic forces on the hull due to PMM motions. Fast Fourier transform (FFT) algorithm is used to filter the hydrodynamic forces/moment from the estimated total force/moment time series. The Fourier series expansion method is used to derive the hydrodynamic derivatives from the estimated force/moment time series. A comparison study is done with the wave-effected hydrodynamic derivatives and derivatives in still water condition.

1 Introduction

Maneuvering predictions are often carried out in still water condition to investigate the maneuverability of the vessel in its early design stages. Practically, ship always does sail in waves; hence for the safety of ship sailing, it is important to capture the wave effects on the maneuvering motion. Maneuvering predictions are usually done by solving maneuvering equations of motion. Estimation of hydrodynamic derivatives forms the basic step in the way of prediction. Hydrodynamic derivatives are derived from the resulting hydrodynamic forces/moments from the captive model tests of ship maneuvering. Several researchers conducted captive model tests experimentally [1,2,3,4] or numerically using computation fluid dynamics (CFD) [5,6,7,8]. Experiments are more reliable for the estimation of hydrodynamic derivatives. The test facilities for the captive model tests are rare, expensive, and time-consuming. Hence, numerical simulation of captive model tests using CFD techniques has gained importance. As ship sails through seaway, the effect of wave will alter the hydrodynamic forces acting on the hull, subsequently the hydrodynamic derivatives also have a considerable variation with the influence of wave. The quantitative estimation of the change of hydrodynamic derivatives with respect to wave will be more useful for the accurate prediction of maneuvering characteristics of vessel. Xu et al. [9] carried out planar motion mechanism tests in irregular waves to investigate the effects of varying wave drift forces on the ship steering characteristics, and the author concluded that significant value of the wave drift damping is induced during pure sway motion of ship in irregular waves. Yasukawa [10, 11] carried out direct maneuvering tests in both regular and irregular waves with container ship model. Model test in regular waves is carried out in head and beam waves, and long- and short-crested waves are selected for irregular wave study.

This paper presents the numerical studies conducted on a container ship in head sea condition to understand the effect of waves on the hydrodynamic derivatives using pure sway and pure yaw modes of planar motion mechanism simulated in a CFD environment.

2 Nomenclature

B :

Beam (m)

C _B :

Block coefficient

D :

Depth (m)

$f_{x}$ :

Surge force amplitude (kN/m)

$f_{y}$ :

Sway force amplitude (kN/m)

$I_{Z}$ :

Moment of inertia in z-direction

L _BP :

Length between perpendiculars (m)

m :

Mass of the ship (kg)

$m_{z}$ :

Yaw moment amplitude

$N_{\delta }$ :

Rudder deflection derivative in z-direction

$N_{{\dot{r} }}$ :

Hydrodynamic coupled derivative of yaw moment with respect to yaw acceleration

$N_{r}$ :

Hydrodynamic linear coupled derivative of yaw moment with respect to yaw rate

$N_{rrr}$ :

Hydrodynamic third-order coupled derivative of yaw moment with respect to yaw rate

$N_{{\dot{v}}}$ :

Hydrodynamic coupled derivative of yaw moment with respect to sway acceleration

$N_{v}$ :

Hydrodynamic linear coupled derivative of yaw moment with respect to sway acceleration

$N_{vvv}$ :

Hydrodynamic third-order coupled derivative of yaw moment with respect to sway velocity

$N_{vvr}$ :

Hydrodynamic third-order cross-coupled derivative of yaw moment with respect to sway velocity and yaw rate

$N_{vrr}$ :

Hydrodynamic third-order cross-coupled derivative of yaw moment with respect to sway velocity and yaw rate

r :

Yaw rate (rad/s)

$\dot{r}$ :

Yaw acceleration (rad/s²)

$t_{r}$ :

Thrust deduction factor

$T_{\text{p}}$ :

Propeller thrust

T _a :

Draft at the aft end (m)

T _m :

Mean draft (m)

T _f :

Draft at the fore end (m)

u :

Linear velocity in surge direction (m/s)

$\dot{u}$ :

Linear acceleration in surge direction (m/s²)

v :

Linear velocity in sway direction (m/s)

$\dot{v}$ :

Linear acceleration in sway direction (m/s²)

∇:

Displaced volume (m³)

$\delta$ :

Rudder angle (rad)

$X_{\delta }$ :

Rudder deflection derivative in x-direction

$X_{rr}$ :

Hydrodynamic second-order coupled derivative of surge force with respect to yaw rate

$X_{{\dot{u}}}$ :

Hydrodynamic uncoupled derivative in surge with respect to surge acceleration

$X_{uu}$ :

Hydrodynamic second-order uncoupled derivative of surge with respect to surge velocity

$X_{vv}$ :

Hydrodynamic second-order coupled derivative of surge force with respect to sway velocity

$X_{vr}$ :

Hydrodynamic second-order cross-coupled derivative of surge force with respect to sway velocity and yaw rate

$Y_{\delta }$ :

Rudder deflection derivative in y-direction

$Y_{{\dot{r}}}$ :

Hydrodynamic coupled derivative of sway force with respect to yaw acceleration

$Y_{r}$ :

Hydrodynamic linear coupled derivative of sway force with respect to yaw rate

$Y_{rrr}$ :

Hydrodynamic third-order coupled derivative of sway force with respect to yaw rate

$Y_{{\dot{v}}}$ :

Hydrodynamic coupled derivative of sway force with respect to sway acceleration

$Y_{v}$ :

Hydrodynamic linear coupled derivative of sway force with respect to sway velocity

$Y_{vvv}$ :

Hydrodynamic third-order coupled derivative of sway force with respect to sway velocity

$Y_{vvr}$ :

Hydrodynamic third-order cross-coupled derivative of sway force with respect to sway velocity and yaw rate

d :

Distance between two oscillators (m)

$\omega_{0}$ :

Frequency of oscillation (rad/sec)

$\omega_{e }$ :

Encountering frequency (rad/s)

U _m :

Model forward speed (m/s)

$Y_{vrr}$ :

Hydrodynamic third-order cross-coupled derivative of sway force with respect to sway velocity and yaw rate

$y_{0a }$ :

Amplitude of transverse oscillation (m)

3 Mathematical Model

Mathematical model of Son and Nomoto [3] representing maneuvering equations of motion in three degrees of freedom for a high-speed container ship is given by

$$ (m - X_{{\dot{u}}} )\,\dot{u} + (m - Y_{{\dot{v}}} )\,vr = X $$

(1)

$$ (m - Y_{{\dot{v}}} )\,\dot{v} + (m - X_{{\dot{u}}} )\,ur - Y_{{\dot{r}}} \dot{r} = Y $$

(2)

$$ (I_{Z} - N_{{\dot{r}}} )\,\dot{r} + N_{{\dot{v}}} \dot{v} = N $$

(3)

where X, Y, N are expressed as hull force/moment due to motion in the surge (x) and sway (y) directions and are given by

$$ \begin{aligned} X & = X(u) + (1 - t_{r} )T_{\text{P}} + X_{vr} vr + X_{vv} v^{2} + X_{rr} r^{2} \\ & \quad + X_{\delta } \sin \delta + f_{x} \sin \,(\omega_{e} t + \varepsilon ) \\ \end{aligned} $$

(4)

$$ \begin{aligned} Y & = Y_{v} v + Y_{r} r + Y_{vvv} v^{3} + Y_{rrr} r^{3} + Y_{vvr} v^{2} r + Y_{vrr} vr^{2} \\ & \quad + Y_{\delta } \cos \delta + f_{y} \sin \,(\omega_{e} t + \varepsilon ) \\ \end{aligned} $$

(5)

$$ \begin{aligned} N & = N_{v} v + N_{r} r + N_{vvv} v^{3} + N_{rrr} r^{3} + N_{vvr} v^{2} r + N_{vrr} vr^{2} \\ & \quad + N_{\delta } \cos \delta + m_{z} \sin \,(\omega_{e} t + \varepsilon ) \\ \end{aligned} $$

(6)

Wave excitation forces/moments are added in the right-hand side of equation of motion. These forces are calculated for the container ship using 2-D strip theory-based program, SEAWAY. Rudder and propeller derivatives in the right-hand side of equation of motion are independent terms, and these equations of motion are found out using empirical relations.

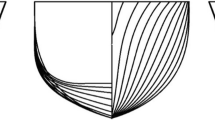
Two right-handed coordinate systems are used to represent the ship motion in the present study (Fig. 2), earth-fixed and ship coordinate systems, where $x_{\text{OG}}$, $y_{\text{OG}}$ represent the position of center of gravity of the ship with respect to earth-fixed coordinate system and ψ is the heading or yaw angle which refers to the direction of the ship and β is the drift angle defined as the angle between resultant velocity in ship-fixed coordinate system and the longitudinal axes in earth-fixed coordinate system. A container ship (S175) has been used for the present study; the principal particulars of the ship are given in Table 1 and body plan in Fig. 1.

Table 1 Main particulars of the container ship and model

Fig. 1

Body plan of S175 container ship

Fig. 2

Earth-fixed and ship-fixed coordinate systems

4 Numerical Simulation

4.1 PMM Tests

Planar motion mechanism (PMM) tests are experimental captive model tests conducted to determine acceleration and velocity-dependent derivatives appearing in the maneuvering equations of motion. PMM consists of two transverse oscillators, one at the bow and one at the stern position of the ship model, oscillated at prescribed motion amplitude y_0a, frequency ω₀, and phase angle 2ε while the model is towed at the speed U₀. Phase angle 2ε between two oscillators determines the modes of operation of PMM. Total forces/moments acting on the hull are measured by the dynamometer placed at the stern (S) and bow (B) of the model (Fig. 3). Present paper includes pure sway and pure yaw modes of simulation in head sea waves.

Fig. 3

Model setup in PMM test

Pure sway Test

Pure sway test is used to determine sway-dependent velocity and acceleration derivatives appearing in the mathematical model. Phase angle 2ε between the oscillators at the bow and stern of the model is made zero, so that ship undergoes translational motion in y-direction. Model kinematic parameters are represented as:

Transverse displacement,

$$ y_{0} = - y_{0a} \sin \omega_{0} t $$

(7)

Transverse velocity,

$$ \dot{y}_{0} = - y_{0a} \omega_{0} \cos \omega_{0} t $$

(8)

Transverse acceleration,

$$ \ddot{y_{0}} = y_{0a} \omega_{0}^{2} \sin\omega_{0} t $$

(9)

Pure Yaw Test

Pure yaw test is conducted to determine yaw-dependent velocity and acceleration derivatives appearing in the mathematical model. Phase angle between fore and aft oscillators 2ε must satisfy the condition given by the expression, $\tan \varepsilon = d\omega /2U_{\text{m}}$. Model kinematic parameters are given by:

Yaw angle,

$$ \varphi = - \varphi_{a} \cos \omega_{0} t $$

(10)

Yaw rate,

$$ \dot{\varphi } = - \varphi_{a } \omega_{0 } \sin \omega_{0} t $$

(11)

Yaw acceleration,

$$ \ddot{\varphi } = - \varphi_{a} \omega_{0}^{2} \cos \omega_{0} t $$

(12)

Numerical simulation of PMM experiments in head sea waves is carried out using RANS-based CFD software. Computational domain larger than International Towing Tank Conference (ITTC) [12] is selected for the numerical simulation of pure sway and pure yaw tests in waves due to the increased hydrodynamic disturbance in the presence of waves compared to still water condition. The fluid domain for dynamic simulation extends 4 L_PP from the aft, 2 L_PP from the bow, 3 L_PP from each of port and starboard sides, and 1 L_PP each from keel to bottom side, where L_PP is the length between perpendiculars (Fig. 4). Boundaries of a domain are composed of velocity inlet for inlet boundary, downstream pressure at outlet boundary, wall with no slip for the hull, and wall with slip for the ship.

Fig. 4

Computational domain for PMM test in waves

An unstructured trimmed hexahedral cell with prismatic near-wall layers is selected to capture the flow properties around the hull surface. Rectangular volumetric block with high resolution is selected to resolve the free surface (Fig. 5). Around 40 grid points per wave length are used to capture the wave in longitudinal direction, and 20 grid points in the vertical direction are implemented to resolve the free surface (Fig. 6).

Fig. 5

Mesh generated for pure sway test

Fig. 6

Water surface captured for pure sway test in head sea waves

Transient finite volume simulations employed an implicit unsteady with a segregated (predictor–corrector) flow solver and semi-implicit method for pressure-linked equations (SIMPLE) solution algorithm. Second-order upwind spatial and first-order temporal discretization schemes are used. Based on the prior studies, SST (Menter) k–ω turbulence model is implemented [7, 13]. The transient simulation is initialized at t = 0, and appropriate time step Δt is chosen based on the velocity of flow and also on grid size in the direction of flow. Grid independence study is carried out for the proper selection of grid size.

5 Analysis

Fourier series expansion method is used for deriving hydrodynamic derivatives from estimated hydrodynamic forces/moments. In this method, obtained hull forces/moments are numerically integrated over the full cycle using trapezoidal integration rule to express as sine and cosine terms and which are compared with the coefficients of the mathematical model of Son and Nomoto [3]. Hydrodynamic forces and moments on the ship hull can be expressed as

$$ f(t) = \sum\limits_{m = 0}^{\infty } {(a_{m} \cos m\omega_{0} t + b_{m} \sin m\omega_{0} t)} $$

(13)

$$ a_{0} = \frac{1}{T}\int\limits_{0}^{T} {f(t)\;{\text{d}}t} $$

(14)

$$ a_{m} = \frac{2}{T}\int\limits_{0}^{T} {f(t)\cos m\omega_{0} t\;{\text{d}}t} $$

(15)

$$ b_{m } = \frac{2}{T}\int\limits_{0}^{T} {f(t)\sin m\omega_{0} t\;{\text{d}}t} $$

(16)

6 Results and Discussion

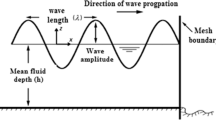
Pure sway and pure yaw modes of PMM are numerically simulated for a container ship in head sea condition with a model wave height of 0.056 m and model wave period of 2 s (Table 1 gives prototype and model details). Estimated total forces/moments from the pure sway mode of PMM tests include both hydrodynamic forces and wave forces (Figs. 7, 8 and 9). Hence, for deriving the hydrodynamic derivatives, hydrodynamic forces need to be filtered from the estimated total forces. Fast Fourier transform (FFT) technique is used to convert the obtained time series to frequency domain signal. From frequency plots (Figs. 10 and 11), lowest frequency peak corresponding to prescribed frequency of PMM oscillation is separated, and this lower frequency signal is converted to time domain (Figs. 12, 13 and 14) for deriving hydrodynamic derivatives.

Fig. 7

Surge force in PMM pure sway mode in wave condition

Fig. 8

Sway force in PMM pure sway mode in wave condition

Fig. 9

Yaw moment in PMM pure yaw mode in wave condition

Fig. 10

Frequency domain representation of sway force in PMM pure sway mode

Fig. 11

Frequency domain representation of yaw moment in PMM pure sway mode

Fig. 12

Surge force in PMM pure sway mode (with and without wave effect)

Fig. 13

Sway force in PMM pure sway mode (with and without wave effect)

Fig. 14

Yaw moment in PMM pure sway mode (with and without wave effect)

Estimated forces and moments from the pure yaw mode of PMM simulation are shown in Figs. 15, 16 and 17. Forces/moment time signal contains noises, and it is filtered using FFT technique. Lower frequency peak in frequency domain plot (Figs. 18 and 19) is filtered and converted to time domain (Figs. 20, 21 and 22). Hydrodynamic derivatives are derived from the filtered time series using Fourier series expansion method and are compared with the calm water derivatives (Tables 2 and 3). Variation of turning parameters in waves is analyzed (Tables 3 and 4).

Fig. 15

Surge force in PMM pure yaw mode in wave condition

Fig. 16

Sway force in PMM pure yaw mode in wave condition

Fig. 17

Yaw moment in PMM pure yaw mode in wave condition

Fig. 18

Frequency domain representation of sway force in PMM pure yaw mode

Fig. 19

Frequency domain representation of yaw moment in PMM pure yaw mode

Fig. 20

Surge force in PMM pure yaw mode (with and without wave effect)

Fig. 21

Sway force in PMM pure yaw mode (with and without wave effect)

Fig. 22

Yaw moment in PMM pure yaw mode (with and without wave effect)

Table 2 Wave effect on hydrodynamic derivatives (pure sway test)

Table 3 Wave effect on hydrodynamic derivatives (pure yaw test)

Table 4 Wave effect on turning parameters

7 Conclusion

In the present study, pure sway and pure yaw tests of planar motion mechanism are carried out for container ship in head sea condition, and dependency of hydrodynamic derivatives on head waves is investigated. CFD analyses are performed, and it is observed that sway-dependent and yaw-dependent hydrodynamic derivatives appearing in the maneuvering equation of motion varied significantly in the presence of waves. First-order velocity-dependent derivatives obtained from pure sway test like $Y_{v}^{{\prime }}$ and $N_{v}^{{\prime }}$ show a variation up to 20% in the presence of waves. Sway-dependent third-order derivative $Y_{vvv}^{{\prime }}$ shows a higher variation up to 111.38% from still water condition to wave condition, but yaw-dependent third-order derivatives $N_{vvv}^{{\prime }}$ show a less variation of 13% for the same condition. Similarly, first-order derivatives obtained from pure yaw test like $Y_{r}^{{\prime }} ,N_{r}^{{{\prime } }}$ show a variation up to 18% in the presence of head sea condition and acceleration derivatives like $Y_{{\dot{r}}}^{{\prime }}$, $N_{r}^{{\prime }}$ show a variation of 16 and 7% respectively for the same. Third-order derivatives obtained from pure yaw tests like $Y_{rrr}^{{\prime }} ,N_{rrr}^{{\prime }}$ show a higher variation of 27.5, 79.02% respectively in wave condition compared to calm water. The effect of these derivatives on turning circle maneuver is investigated. Turning circle radius and tactical diameter of the vessel are found to be reduced by 16.08, 20.39% respectively compared to calm water condition. Advance and transfer also have a considerable variation up to 25%, and the trajectory in waves is found to drift toward the direction of wave propagation. The results of simulation indicated that wave has a considerable influence on hydrodynamic derivatives and effects of wave on ship maneuverability cannot be neglected and this study can be extended by conducting the combined mode of PMM simulation in the same wave condition to simulate the maneuvering trajectory of ship in waves.