Keywords

1 Introduction

Extreme wave conditions influence all the coastal and offshore engineering applications. Therefore, the prediction of extreme wave climate is prerequisite for a variety of coastal activities like the structural design of port and harbour infrastructures, optimisation of marine energy converters, planning of beach management schemes and for flood risk analysis. In recent years, marine energy from tidal currents and waves [1, 2] has been identified as an important source of low carbon sustainable energy. This incentive is evident in the countries with large potential for exploiting these wave energy resources like Australia, the UK and also developing countries like India. This is imperative as the prevailing marine environment is expected to change in the coming years due to global warming.

Regarding the efficiency and survivability of the marine energy-converting devices, coastal and offshore structures, one critical factor is the information on the prevailing extreme sea-state parameters in the vicinity of these structures, like 100 and 1000-year extreme wave heights. The lesser return period would be associated with a lesser wave height return values but more risk and vice versa, depending on the structural importance. The design wave provides ample opportunity to decide on the risk involved as it is associated with a return period that is proportional to the life of the structure. For example, in the design of sea defences safety control system of The Netherlands, return values of up to 10,000-year are used as the country lies below the mean sea level. Also for flood risk area mapping in the UK, a 1000-year return value is used.

Any underestimation of these extreme conditions could adversely affect the survivability of the structures leading to catastrophic failure, while an overestimate would inevitably lead to over design, making the return on investment financially unattractive. The understanding of extreme conditions of waves is of interest not only to the research community but also to the industries because of the economic aspect. Any traditional method of estimating extreme wave heights consists of gathering all the available Hs data for a number of years in a single sample and fitting a suitable parametric model to the data. As the extreme values are unique occurrence events and fall outside the range of the available observations, which implies that an extrapolation to the desired low probability of occurrence is required [3,4,5].

Many researchers in the past have proposed different approaches for extreme wave analysis. As there are no theoretical means to determine the most appropriate method for extreme wave analysis, a number of methods were typically used in different studies and the one achieving the best fit to the data and the method which results in reliable return values generally is being accepted.

In many studies, the interest is being centred on identifying the most reliable approach for estimating the extreme order statistics. Samayam et al. [6] investigated different approaches for the return value estimation like the generalised extreme value distribution (GEV) method based on annual maxima sample, the generalised Pareto distribution (GPD) method based on peaks over threshold sample, equivalent triangular storm (ETS) model based on the concept of replacing the sequence of actual storms with a sequence of equivalent triangular storms and the polynomial approximation method [7] based on extrapolating the tail of the provision function. In their study, they have also introduced a statistical approach to validate the reliability of the return values from a particular extreme wave estimation method and thereby identified GEV and GPD methods showing high variation in underestimating or overestimating of return values whereas the polynomial approximation method showed consistency in estimating return values for both buoy and simulated data. Hence, in this study, the extreme wave heights for different return periods were estimated by considering the polynomial approximation method of extreme wave analysis.

Majority of the Indian seas experience comparatively mild waves under normal weather conditions. When strong monsoon winds prevail due to cyclones, higher waves can be experienced at the exposed locations. When these cyclones pass over or in the close vicinity of the shore, which results in higher wave heights. Extreme wave conditions in India occur mainly due to tropical cyclones. Isolated maritime structures such as wind turbine towers and oil-drilling rigs have to be designed to resist the largest possible wave at the site. In view of this variable and often unpredictable character of the wave forces to which marine structures are subjected to, it is of utmost importance to arrive at the design wave height with greater caution after a rigorous analysis. Hence, in the present study, the extreme wave heights for different return periods were estimated not only for Hs but also for Hmax, assuming the individual wave height measurements are Rayleigh distributed.

2 Description of the Significant Wave Height Data and Study Area

For the modelling of extreme wave conditions in space and time, space-time significant wave height (Hs) data is needed. It is evident that a quality data set with sufficient resolution in both time and space is a necessary requirement for a better prediction of the extremes. Several sources of data acquisition have been explored such as observations from in situ measurements, altimeter measurements, modelling of waves from winds and also data assimilation techniques. In this particular study, we chose ERA-Interim significant wave height data from European Centre for Medium-Range Weather Forecasts (ECMWF) because they have a regular coverage for the whole World Oceans, in particular, the Indian coast. The wave climate parameters with 6-hourly fields covering the whole globe can be obtained, with the best spatial resolution of 0.125° × 0.125°. Furthermore, these numerically simulated ERA-Interim wave data sets have regular and long continuous series, which is important for the statistical aims of extreme wave analysis.

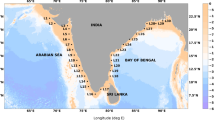
The Indian coastline has a wide territory which extends from 5°N to 25°N latitudes and at longitudes, 65°E–90°E. In order to carry out the extreme wave analysis, 11 important major port locations in India were considered. The selected sites are shown in Fig. 1 and presented in Table 1 along with their coordinates. The main criterion for the choice of these locations is the rapid development of major infrastructure in and around these port locations. The estimates of extreme wave height return values are based on ERA-Interim significant wave height data, covering a period of 36 years i.e., from 1979 to 2014 obtained by extracting this data of resolution 0.125° × 0.125° nearest to the selected port locations.

Fig. 1
figure 1

Major port locations along the Indian coast

Full size image
Table 1 Coordinates of the major ports along the Indian coast and extreme wave heights (m) for different return periods
Full size table

3 Methodology of Polynomial Approximation Method

The polynomial approximation method involves the construction of an analytical approximation Fap(H), aimed for its extrapolation beyond an observed maximum value HM. The approximation should be restricted to a shorter domain lying above the uppermost mode of the histogram considered of the function F(H). The domain suitable for constructing approximation Fap(H) can be determined by the following condition,

$$H_{\text{l}} \le H \le H_{\text{h}} \le H_{\text{M}}$$
(1)

where Hl and Hh are the lower and the upper edges of the domain of F(H).

The number of points (NM) considered in the histogram is HM/ΔH and NS is defined as,

$$N_{\text{S}} = \left( {H_{\text{M}} - H_{\text{h}} } \right) /\Delta H$$
(2)

The number of points (NT) used for constructing the approximation function, Fap(H) is defined as,

$$N_{\text{T}} = \left( {H_{\text{h}} - H_{\text{l}} } \right) /\Delta H + 1$$
(3)

The approximation function, Fap(H) should be constructed in the logarithmic coordinates due to few values in the tail of F(H), providing importance to the values in the tail. This allows accounting for a strong variability of the tail of function F(H) in the domain near the maximum value of the series (HM) depending on the length of the series.

To exclude the application of fixed statistics, the approximation function Fap(H) should be considered in the form of a polynomial of degree n, the value of which may vary.

The statistical distribution fitted to the provision function is given as,

$$F_{\text{ap}} (H) = \exp \left[ {\sum\limits_{i = 0}^{i = n} {a_{k} H^{k} } } \right]$$
(4)

After obtaining the approximation function, Fap(H) from Eq. (4), the return value, HR, appearing once for NR years, can be deduced from the following formula,

$$F(H_{R} ) = \Delta t/8760 \cdot N_{R}$$
(5)

where \(\Delta t\) is the interval of significant wave height data observations.

4 Analysis of Extreme Waves Using Significant Wave Height Data

The polynomial approximation method has been used to evaluate extreme wave heights for different return periods at major port locations. Figure 2 shows the application of polynomial approximation method for a series of Hs at four of the port locations from which we can observe the adaptation of polynomial approximations to the real behaviour of the tail of the provision function. The provision function has been built in logarithmic coordinates due to a fewer number of values in the tail of F(H), ensuring importance to the tail values.

Fig. 2
figure 2

Application of polynomial approximation method for the series of Hs data at Kolkata and Paradip

Full size image

5 Extreme Wave Analysis Using Maximum Wave Height Data

The marine structures and devices operating in marine environments are continuously exposed to the forces from the waves. During extreme events, or over a period of time, for example, by fatigue, wear, corrosion, failure to withstand such forces may lead to severe consequences. Hence, these extreme wave conditions need to be analysed with a high degree of confidence to minimise the chances of such failures to acceptable levels. Even though the future marine environment will tend to be rougher than the historic and current marine environment, the uncertainty of the future wave climate is considerably large. In view of this variable and often unpredictable character of the wave forces to which marine structures are subjected to, it is important to arrive at the design wave height with utmost caution after a rigorous analysis.

According to Liu and Burcharth [8], the conservative method for the estimation of the design individual maximum wave height involves first to obtain the design significant wave height corresponding to a certain exceedance probability within a lifetime of the structure, based on the statistical extreme wave analysis. The design individual maximum wave height is then calculated with the assumption that the individual wave heights follow the Rayleigh distribution, as the expected maximum individual wave height associated with the design significant wave height. According to them, the expected maximum individual Hmax associated with the design Hs is given as,

$$(H_{ \hbox{max} } )_{\text{mean}} \approx \left( {\sqrt {\frac{\ln N}{2}} + \frac{0.577}{{\sqrt {8\ln N} }}} \right)H_{\text{s}}^{100}$$
(6)

where N is the number of individual waves related to \(H_{\text{s}}^{100}\). However, the exceedance probability of such a design individual maximum wave height within the lifetime of the structure is unknown, which calls for an additional site-specific analysis.

In the present study by an assumption that the individual wave heights of ERA-Interim data follow the Rayleigh distribution, in which case Longuet Higgins [9] suggested that the range of Hmax could be 1.6Hs–2Hs. Using this assumption, short-term statistics of individual waves and long-term statistics of sea states may be combined to obtain long-term distributions of individual waves. Hence, in this section, the extreme wave heights for different return periods were estimated not only from Hs but also from the maximum wave heights like 1.6Hs, 1.8Hs and 2.0Hs at the major ports. At each of these locations, the assessment was carried out by the polynomial approximation method of extreme wave analysis.

The resulted return values for different return periods are mentioned as \(H_{{1.6{ \hbox{max} }}}^{R} ,H_{{1.8{ \hbox{max} }}}^{R}\) and \(H_{{2.0{ \hbox{max} }}}^{R}\), respectively. On the other hand, it is illuminating to perceive whether the variability and trend statistics of the \(H_{{1.6{ \hbox{max} }}}^{R} ,H_{{1.8{ \hbox{max} }}}^{R}\) and \(H_{{2.0{ \hbox{max} }}}^{R}\) values are analogous to the values \(1.6H_{\text{s}}^{R} ,1.8H_{\text{s}}^{R}\) and \(2.0H_{\text{s}}^{R}\), which are nothing but the extreme wave heights for different return periods (R) estimated from Hs and multiplied with 1.6, 1.8 and 2.0, respectively. The aforementioned analysis at all of the 11 major port locations along the Indian coast is presented in Fig. 3. From the figures, it can be observed that the trends and slopes of both of the approaches are almost similar at most of the locations except at Kochi. This is because at Kochi the outlier Hs values in the time series are much higher and when these outliers are again multiplied by 1.8 or 2.0, the attained values became more assertive which resulted in anomalous return values. This kind of anomaly can be perceived rarely, but it is a major shortcoming of this approach.

Fig. 3
figure 3

Variation of wave height return values for Hs and Hmax at different port locations along the Indian coast

Full size image

Further comparison of these two different return value series was performed by obtaining the Covariance and Root mean square error (RMSE), which is depicted in Table 2. Covariance is a measure of the joint variability of two different random variables. Therefore, the sign of the covariance shows the tendency in the linear relationship between the variables. The RMSE was estimated in order to check the level of deviation between these two different return value series. From the aforementioned table, we can notice that the covariance values are always positive indicating the similar linear behaviour between them and at Paradip and Kochi, higher RMSE values can be seen, indicating the outlier Hs values, which results in anomalous return values.

Table 2 Statistical relation between different return value series
Full size table

Considering the above observations and results, both the approaches of estimating design individual maximum wave height have several uncertainties, however, the estimated return values \(1.6H_{\text{s}}^{R} ,1.8H_{\text{s}}^{R}\) and \(2.0H_{\text{s}}^{R}\) are very close to the values of \(H_{{1.6{ \hbox{max} }}}^{R} ,H_{{1.8{ \hbox{max} }}}^{R}\) and \(H_{{2.0{ \hbox{max} }}}^{R}\), and the anomalous outlier phenomenon (Kochi in Fig. 3) does not appear in the former approach. Further, this approach is straightforward and results in the same values as that of \(H_{{1.6{ \hbox{max} }}}^{R} ,H_{{1.8{ \hbox{max} }}}^{R}\) and \(H_{{2.0{ \hbox{max} }}}^{R}\). The aforementioned analysis will offer guidance on the design of marine works and structures normally related to the port infrastructure and also for the design of beach management schemes.

6 Conclusions

The polynomial approximation method has been used to evaluate extreme wave heights for different return periods at major port locations along the Indian coast. This awareness aids in the efficient design of the structures related to ports, so as to withstand the wave forces that impact on them resulting from extreme wave conditions during their lifetime. To arrive at the design wave height, a rigorous analysis was carried out with utmost caution by estimating extreme wave heights for different return periods not only from Hs but also from the maximum wave heights like 1.6Hs, 1.8Hs and 2.0Hs and a detailed analogous investigation was carried out between the return values series of \(H_{{1.6{ \hbox{max} }}}^{R} ,H_{{1.8{ \hbox{max} }}}^{R}\) and \(H_{{2.0{ \hbox{max} }}}^{R}\) and \(1.6H_{\text{s}}^{R} ,1.8H_{\text{s}}^{R}\) and \(2.0H_{\text{s}}^{R}\). This analysis will provide an ample opportunity to decide on the risk involved as it is associated with different return periods that is proportional to the life of the port-related structures.