Approximate Bit Error Rate of DPSK with Imperfect Phase Noise in TWDP Fading

Abstract

This study provides closed-form expressions for average bit error rate (ABER) of differential phase shift keying (DPSK) with phase error in two-wave with diffuse power (TWDP) fading. It is considered that the envelope of phase error is Gaussian distributed. The effect of phase synchronization on wireless system is studied for different values of TWDP fading parameters and phase error. The analytical results are evaluated to study the impact of phase error on the system performance. Also, the results are compared with the case of perfectly synchronized.

1 Introduction

The performance of PSK with noisy phase reference has been a topic of interest for many researchers since the 1960s. Initial work on modeling the phase error was done by Tikhonov and Viterbi. Since then a lot of work has been done to study the effect of phase error on different digital modulation schemes over various fading models such as Rayleigh, Nakagami-m and Rician [1,2,3,4,5,6,7]. In all these papers, the effects of imperfect carrier synchronization have been studied by assuming the phase distribution either Gaussian or Tikhonov. However, phase synchronization errors can have a significant effect on the receiver’s capability to make the correct decisions. The problem gets more severe as data rates increase due to phase error. In 2002, a fading model was proposed by Durgin et al. which could be used to model fading scenarios having two specular paths in addition to the diffusely propagating power [8]. This fading model is known as TWDP and can be used to characterize the fading scenarios which are more severe than Rayleigh fading. The practical significance of this model comes from modern uses of wireless channels in applications such as data transmission in dynamic environments such as mobile personal devices (such as smartphones or smart/connected automobiles) and Internet service in aircraft that have become pervasive in recent years.

The existing fading models such as Rayleigh and Rician fading are included in TWDP fading as special cases. The error performance analysis of various digital modulation schemes in TWDP fading is reported in the literature [9,10,11,12]. However, till date no work is available on the analysis of modulation schemes with phase noise error in TWDP fading model. In this paper, we derive the approximate closed-form expression for average BEP of DPSK with noisy phase reference in TWDP fading channel. In Sect. 2, the PDF of TWDP fading model is presented. In Sect. 3, the PDF approach is used to derive the ABER of DPSK with noisy phase reference over TWDP fading model. The numerical results are evaluated and discussed in Sect. 4. Section 5 holds the conclusion of the paper.

2 TWDP Fading Model

The TWDP fading model is having two specular components with some Rayleigh distributed diffuse power. The instantaneous signal-to-noise ratio (SNR) is defined as $\gamma = r^{2} E_{b} /N_{0}$, and the average SNR is defined as $\bar{\gamma } = E\left( {r^{2} } \right)\frac{{E_{b} }}{{N_{0} }}$. The PDF of SNR $(\gamma )$ for TWDP fading channel can be evaluated as [9]:

$$p_{\gamma } \left( \gamma \right) = \frac{\eta }{2}\sum\limits_{i = 1}^{L} {a_{i} \sum\limits_{j = 0}^{1} {\exp \left( { - P_{2i - j} - \eta \gamma } \right)} } I_{0} \left( {2\sqrt {P_{2i - j} \eta \gamma } } \right),$$

(1)

where $\eta = K + 1/\bar{\gamma }$, $P_{2i - j} = K\left[ {1 + \left( { - 1} \right)^{j} \Delta \cos \left( {\pi \left( {\frac{i - 1}{2L - 1}} \right)} \right)} \right]$, $\Delta$ denotes the relative strength of two specular components, K is defined as ratio of specular power to diffuse power, and L is the order of PDF. The TWDP fading can be reduced to special cases [9] of fading such as Rayleigh fading (K = 0) and Rician fading (K > 0, ∆ = 0).

3 Performance Analysis

The conditional BER of DPSK with noisy phase reference over AWGN channel can be expressed as [13]:

$$P\left( {e\text{|}\gamma ,\phi } \right) = \frac{1}{2}\exp \left( { - \gamma \,\cos^{2} \phi } \right),$$

(2)

where ϕ represents the phase error. It is considered that ϕ is Gaussian distributed with zero mean and $2\sigma^{2}$ variance, i.e., CƝ (0, 2σ²). The PDF of ϕ can be given by:

$$p_{\phi } \left( \phi \right) = \frac{1}{{\sqrt {2\pi \sigma^{2} } }}\exp \left( {\frac{{ - \phi^{2} }}{{2\sigma^{2} }}} \right),$$

(3)

The ABER of a modulation scheme with phase noise error over a fading channel can be obtained by performing a twofold integration, first over the PDF of ϕ and second over the PDF of fading model [2],

$$P_{e} = \int\limits_{0}^{\infty } {\int\limits_{ - \pi }^{\pi } {P\left( {e|\gamma ,\phi } \right)p_{\phi } \left( \phi \right)p_{\gamma } \left( \gamma \right){\text{d}}\phi \,{\text{d}}\gamma } } ,$$

(4)

To derive the ABER of DPSK with Gaussian distributed phase error over TWDP fading model, first solve the inner integral of (4) as:

$$P\left( {e|\gamma } \right) = \int\limits_{ - \pi }^{\pi } {P\left( {e|\gamma ,\phi } \right)p_{\phi } \left( \phi \right){\text{d}}\phi } ,$$

(5)

Substitute $P\left( {e\text{|}\gamma ,\phi } \right)$ and $p_{\phi } \left( \phi \right)$ from (2) and (3), respectively, into (5), and we get:

$$P\left( {e\text{|}\gamma } \right) = \int\limits_{ - \pi }^{\pi } {\frac{1}{2}} \exp \left( { - \gamma \,\cos^{2} \phi } \right) \times \frac{1}{{\sqrt {2\pi \sigma^{2} } }}\exp \left( {\frac{{ - \phi^{2} }}{{2\sigma^{2} }}} \right){\text{d}}\phi ,$$

(6)

By using the small angle approximation, $\cos \left( {\Delta \phi } \right) \cong 1 - \frac{{\left( {\Delta \phi } \right)^{2} }}{2}$, (6) can be rewritten as:

$$P\left( {e\text{|}\gamma } \right) = \frac{{\exp \left( { - \gamma } \right)}}{{2\sqrt {2\pi \sigma^{2} } }}\int\limits_{ - \pi }^{\pi } {\exp \left( { - \phi^{2} \left( {\frac{1}{{2\sigma^{2} }} - \gamma } \right)} \right){\text{d}}\phi } ,$$

(7)

Now by employing the general formula, i.e., $\int_{ - \pi }^{\pi } {\exp \left( { - x^{2} } \right){\text{d}}x} \simeq \sqrt \pi$, the conditional BER of DPSK with Gaussian phase error over AWGN channel can be expressed as:

$$P\left( {e\text{|}\gamma } \right) = \frac{{\exp \left( { - \gamma } \right)}}{{2\sqrt {1 - 2\sigma^{2} \gamma } }},$$

(8)

Now solving the outer integral of (4) over PDF of TWDP fading, we get

$$P_{e} = \int\limits_{0}^{\infty } {P\left( {e\text{|}\gamma } \right)p_{\gamma } \left( \gamma \right){\text{d}}\gamma } ,$$

(9)

By substituting $P\left( {e\text{|}\gamma } \right)$ and $p_{\gamma } \left( \gamma \right)$ from (8) and (1) into (9), we get:

$$P_{e} = \int\limits_{0}^{\infty } {\frac{{\exp \left( { - \gamma } \right)}}{{2\sqrt {1 - 2\sigma^{2} \gamma } }}} \times \frac{\eta }{2}\sum\limits_{i = 1}^{L} {a_{i} } \sum\limits_{j = 0}^{1} {\exp \left( { - P_{2i - j} - \eta \gamma } \right)} I_{0} \left( {2\sqrt {P_{2i - j} \eta \gamma } } \right){\text{d}}\gamma ,$$

(10)

Put $\sigma_{\phi }^{2} = \left( {C\gamma } \right)^{ - 1}$ in (10), and rearrange (10) as:

$$P_{e} = \frac{\eta }{4}\sum\limits_{i = 1}^{L} {a_{i} } \sum\limits_{j = 0}^{1} {\exp \left( { - P_{2i - j} } \right)\frac{1}{{\sqrt {1 - \frac{2}{C}} }}} \int\limits_{0}^{\infty } {\exp \left( { - \gamma \left( {1 + \eta } \right)} \right)} I_{0} \left( {2\sqrt {P_{2i - j} \eta \gamma } } \right){\text{d}}\gamma ,$$

(11)

By using the formula given in the appendix, the final ABER expression is calculated as:

$$P_{e} = \frac{\eta }{4}\sum\limits_{i = 1}^{L} {a_{i} } \sum\limits_{j = 0}^{1} {\exp \left( { - P_{2i - j} } \right)} \left( {1 - \frac{2}{C}} \right)^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0pt} 2}}} \times \frac{1}{1 + \eta }M\left( {1;1;\frac{{P_{2i - j} \eta }}{1 + \eta }} \right),\quad {\text{C}} > 2.$$

(12)

where M(a; b; c) is confluent hypergeometric function.

4 Numerical Results and Discussion

The numerical results are provided for the ABER of partially coherent differential PSK over TWDP fading model. By using (12), the results are plotted in Figs. 1, 2, and 3. As mentioned in (12), these results are valid only for value of C greater than 2. The results are taken for different parameters such as C, Δ, and K. The value of imperfect synchronization factor (C) is taken to be 3, 10, and ∞. When C = ∞, the DPSK modulation is considered to be having no phase error. For low values of C, the phase error is more, and as expected, the degradation is severe. As value of C increases, the degradation becomes less severe and closer to the perfectly synchronization case.

Fig. 1

ABER versus SNR for DPSK with phase error with fixed K and varying C and Δ

Fig. 2

ABER versus SNR for DPSK with phase error with fixed Δ and varying C and K

Fig. 3

ABER versus C (in dB) for DPSK modulation for fixed K, SNR, and Δ

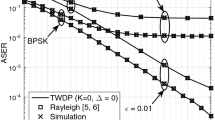
In Fig. 1, results are plotted for a combination of different values of C and ∆ and for fixed value of K. It is observed that the performance of system deteriorates as ∆ approaches 1.

Similarly, in Fig. 2, results are plotted for fixed value of ∆ with different values of C and K. The results demonstrated that the ABER decreases as the value of specular power (K) increases.

Figure 3 shows the results for ABER versus C for fixed values of ∆, K, and SNR (in dB). The plot depicts that the performance of system improves as the value of C increases; i.e., as the phase error decreases, the ABER also decreases.

5 Conclusion

This paper analyzed the performance of ABER of partially coherent DPSK in TWDP fading channels. The closed-form expressions are derived for ABER which is a convenient tool for error performance analysis. The final expression of unconditional ABER of DPSK along with Gaussian phase error over TWDP fading is valid only for value of C greater than 2. The analysis depicted that if the imperfect synchronization factor, ‘C’ increases; the system performance is improved and is closed to perfectly synchronization case.

Appendix

The expression in (11) can be further solved by using identity given in ([14], 6.6.14.3) as:

$$\int\limits_{0}^{\infty } {\exp \left( { - \alpha x} \right)} I_{2v} \left( {2\sqrt {\beta x} } \right){\text{d}}x = \frac{1}{{\sqrt {\alpha \beta } }}\exp \left( {\frac{\beta }{2\alpha }} \right)\frac{{\Gamma \left( {v + 1} \right)}}{{\Gamma \left( {2v + 1} \right)}}M_{ - 1/2,v} \left( {\frac{\beta }{\alpha }} \right)$$

Now, (11) can be simplified as:

$$\begin{aligned} P_{e} & = \frac{\eta }{4}\sum\limits_{i = 1}^{L} {a_{i} } \sum\limits_{j = 0}^{1} {\exp \left( { - P_{2i - j} } \right)} \left( {1 - \frac{2}{C}} \right)^{ - 1/2} \exp \left( {\frac{{P_{2i - j} \eta }}{{2\left( {1 + \eta } \right)}}} \right) \\ & \quad \times \frac{1}{{\sqrt {\left( {1 + \eta } \right)P_{2i - j} \eta } }}M_{ - 1/2,0} \left( {\frac{{P_{2i - j} \eta }}{1 + \eta }} \right) \\ \end{aligned}$$

(13)

Use $M_{k,s} \left( z \right) = \exp \left( {\frac{ - z}{2}} \right)z^{s + 1/2} M\left( {s - k + \frac{1}{2};1 + 2s;z} \right)$ [14] in (13), and the final equation can be obtained as given in (12).