Keywords

1 Introduction

Many authors have analyzed the thermal convection in a horizontal fluid-saturated porous medium, but very few have dealt with the thermal convection in an inclined porous layer in the last decade. The current investigation on thermal convection caused by an internal heat generation with an inclined porous medium is vital due to many real-life problems such as geophysical, the hydrology of aquifers, underground energy, transport and environmental problems, etc. The interest in the inclined porous layer with the thermal convective instability situation arises most relative to the transport in groundwater and in the exploitation of geothermal reservoirs. Other important areas are like the transport of pollutants, oil extracting, and food processing [1, 2]. The mechanism of thermal transport has a major application in environmental problems [3]. The convection in porous layer has been surveyed in the literature [4, 5].

In the literature first time, the inclined porous medium is analyzed by Bories and Combarnous [6], and later, it is extended by Weber [7]. Improving these studies, an inclined porous medium was continued by Caltagirone and Bories [8]. Rees and Bassom [9] studied the thermal convection properties in an inclined layer, and they mentioned some of the outstanding results using linear stability analysis. Thermal convection in a saturated porous layer with internal heat source and mass flow is studied by Matta et al. [10]. The fluid flow in an inclined porous layer is carried out by Barletta and Storesletten [11], and further a fixed heat flux along the walls of the inclined porous medium is studied by Rees and Barletta[12]; also, the thermal convection of Darcy flow in an inclined layer is extended by Barletta and Rees [13]. A note is also given by Nield [14] on the inclined porous layer to give the answers for well-preferred patterns of the natural thermal convection, and then after, Nield et al. [15] find out the importance of the viscous dissipation effect of thermal instability in an inclined porous layer. A little set of articles on the inclined porous medium is available in the surveyed book of Nield and Bejan [16].

The importance of this analysis is to study the thermal convection on the inclined porous medium with the influence of an internal heat source. The applied thermal gradient and heat source lead to a possibly thermal instability in the inclined porous medium. The problem stated that equations have been modified as an eigenvalue problem, which is evaluated numerically by applying the Chebyshev-Tau method.

Fig. 1
figure 1

The physical system

Full size image

2 Mathematical Formulation

Let us choose an infinite length-inclined fluid-saturated porous layer with vertical height H considered as shown in Fig. 1. The inclination angle of porous layer is \(\phi \), which is along the \(x^{*}\)-axis. \(z^{*}\)-axis is taken vertically upward. The vertical thermal difference along the walls is \(\triangle {T}\). The fluid flow inside the porous medium is applicable the Darcy law and Boussinesq approximation. The governing equations in nondimensional form are

$$\begin{aligned} \nabla \cdot {\mathbf{{q}}=0} \;, \end{aligned}$$
(1)
$$\begin{aligned} \mathbf{{q}}+ \nabla {P}=R_z\theta \left[ \sin (\phi )e_{1}+\cos (\phi )e_{3}\right] \;, \end{aligned}$$
(2)
$$\begin{aligned} \frac{\partial {\theta }}{\partial {t} } +\mathbf{{q}}\cdot \nabla \theta =\nabla ^{2}\theta +Q\;, \end{aligned}$$
(3)

and the corresponding boundary conditions are

$$\begin{aligned} \left. \begin{matrix} z = 0\; : \quad w = 0, \quad \theta = 1 \\ z = 1\; : \quad w = 0, \quad \theta = 0 \end{matrix}\right\} \end{aligned}$$
(4)

The corresponding dimensionless variables were used for dimensionless governing equations,

$$\begin{aligned} \left( x,y,z\right) = \frac{1}{H}\left( x^{*},y^{*},z^{*}\right) , \quad t= \frac{\alpha _{m}t^{*}}{aH^{2}}\;, \quad \mathbf{q}= \frac{H\mathbf{q}^{*}}{\alpha _{m}}\;, \quad P = \frac{{K}P^{*}}{\mu \alpha _{m}}, \end{aligned}$$
$$\begin{aligned} T^{*}=T_0+\theta {\triangle T }\;, \quad Q =\frac{H^{2}Q^{*}}{k_{m}{\triangle T }}, \end{aligned}$$
(5)

where

$$\begin{aligned} \alpha _m=\frac{k_{m}}{\left( \rho c_p\right) _f},a=\frac{\left( \rho c\right) _m}{\left( \rho c_p\right) _f}, R_z= \frac{\rho _{0}g\gamma _{T}KH\triangle T}{\mu \alpha _{m}}. \end{aligned}$$
(6)

Here, the velocity is notated as \(\mathbf{q}^{*}\), \(T^{*}\) is the temperature, \(P^{*}\) is the pressure, \(Q^{*}\) is a heat source, and g is the gravitational acceleration, where the subscripts m and f are referred to porous medium and fluid, respectively. Here, K is the permeability of the porous layer. Also, \(\rho \), c, \(k_{m}\), and \(\mu \) denote the density, specific heat, thermal conductivity, and viscosity, respectively. Also, \(\gamma _{T}\) is the thermal expansion coefficient and the vertical thermal Rayleigh number is \(R_z\).

3 Basic State Solution

The nondimensional governing Eqs. (1)–(3), corresponding to (4), has a steady-state solution as follows:

$$\begin{aligned} u_{s} =u\left( z\right) \;, v_{s} =0,w_{s} =0, P_{s} =P\left( x,y,z\right) ,\theta _{s}=\theta \left( z\right) \;. \end{aligned}$$
(7)

There is no net flow along the x-axis, and then \(\int ^{1}_{0}u(z)dz=0\). Hence, the steady-state solution is in the form of flow velocity and temperature in the given porous layer.

$$\begin{aligned} u_s=R_z\sin (\phi )\left[ \frac{Q}{2}\left( z-z^2-\frac{1}{6}\right) -z+\frac{1}{2}\right] \;, \end{aligned}$$
$$\begin{aligned} v_s=0 \;, w_s=0, T_{s}=\frac{Q}{2}\left( z-z^2\right) +1-z\;. \end{aligned}$$
(8)

4 Linear Stability Analysis

An arbitrarily disturbance quantities of the basic flow are defined as \(\mathbf{q}=\mathbf{q}_{s} +\epsilon \;\overline{\mathbf{q}}\), \(\theta =\theta _{s} +\epsilon \;\overline{\theta }\) and \(P=P_{s} +\epsilon \;\overline{P}\), where \(\epsilon \) is the perturbation parameter and submitted these disturbances in dimensionless governing Eqs. (1)–(3), and thereafter, by neglecting the nonlinear terms, got the linear system in the following form:

$$\begin{aligned} \nabla \cdot {\overline{\mathbf{q}}=0} \;, \end{aligned}$$
(9)
$$\begin{aligned} \overline{\mathbf{q}}+\nabla \overline{P}=\left[ R_z\overline{\theta }\right] \left( \sin (\phi )e_{1}+\cos (\phi )e_{3}\right) \;, \end{aligned}$$
(10)
$$\begin{aligned} \frac{\partial {\overline{\theta }}}{\partial {t} } +\mathbf{q}_s\cdot \nabla \overline{\theta }+\overline{\mathbf{q}}\cdot \nabla \theta _s=\nabla ^{2}\overline{\theta }\;, \end{aligned}$$
(11)

where

$$\begin{aligned} \nabla \theta _s=\left( 0,0,\frac{{Q}}{2}\left( 1-2z\right) -1\right) . \end{aligned}$$

The boundary conditions at the walls are

$$\begin{aligned} \left. \begin{matrix} z = 0\; : \quad \overline{w} = 0, \quad \overline{\theta } = 1 \\ z = 1\; : \quad \overline{w} = 0, \quad \overline{\theta } = 0\; \end{matrix}\right\} \end{aligned}$$
(12)

These conditions in Eq. (12) are clear that there is a zero perturbation in the velocity and temperature along the plates. The solution of Eqs. (9)–(11) funded in the form of normal modes

$$\begin{aligned} \left[ \overline{P},\overline{\theta },\overline{\mathbf{q}} \right] =\left[ P\left( z\right) ,\theta \left( z\right) ,\mathbf{q}\left( z\right) \right] \exp \left\{ i\left[ k{x}+l{y}\right] +\sigma {t}\right\} \;, \end{aligned}$$
(13)

thereafter eliminates P from Eq. (10), and we get

$$\begin{aligned} \left( D^{2}-\alpha ^{2}\right) w+\left( \alpha ^{2}\cos (\phi )\theta +{i}k{\sin (\phi )}D\theta \right) R_z=0, \end{aligned}$$
(14)
$$\begin{aligned} \left( D^{2}-\alpha ^{2}-{i}{k}{u_s}\right) \theta - \left( \frac{{Q}}{2}\left( 1-2z\right) -1\right) w=\sigma \theta . \end{aligned}$$
(15)

Here, \(D=\frac{d}{dz}\), and Eqs. (14)–(15) subject to boundary conditions (4) give an eigenvalue problem for thermal Rayleigh number \(R_{z}\) with k and l wave numbers along x and y directions. In the above, \(\alpha =\sqrt{k^{2}+l^{2}}\) is the overall wave number.

5 Results Analysis

The thermal instability analysis in an inclined fluid-saturated porous layer with effect of heat source is studied. The inclination angle \(\phi \) is tested from \(0^\circ \) to \(80^\circ \). The critical thermal Rayleigh number (\(R_{z}\)) is defined as the minimum of all \(R_{z}\) values as the wave number (\(\alpha \)) is varied. The results are shown in Figs. 2, 3, and 4.

Fig. 2
figure 2

Variation of \(R_{z}\) with \(\phi \)

Full size image
Fig. 3
figure 3

Variation of \(R_{z}\) with Q

Full size image
Fig. 4
figure 4

Variation of \(T_s\) with z

Full size image

Variation of \(R_{z}\) is shown as a function of \(\phi \) for different values of Q as given in Fig. 2. In the absence of heat source (\(Q=0\)), the critical value of \(R_{z}\) is increasing slowly upto \(\phi <50^{0}\), and thereafter the value of \(R_{z}\) is increasing very fast, which indicate that as inclination angle increases, the system is stabilizing.

The response of critical values of \(R_{z}\) as a function of heat source (Q) is given in Fig. 3, for the absence and presence of an inclined angle (\(\phi \)). When the internal heat source increases, then the critical \(R_{z}\) values are decreased, which means flow is destabilized due to enhancement of the heat source. The inclination angle (\(\phi \)) is increased from \(0^\circ \) to \(40^\circ \), and then the critical values of \(R_{z}\) also enhance, and it indicates that the flow is stable.

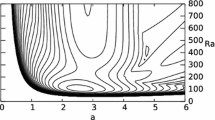
The thermal contours are shown in Fig. 4 in the absence and presence of heat source Q. It is interesting to observe that the thermal profiles are parabolic in the presence of heat source. It is clearly appeared that as an internal heat source increases, the global temperature is also increased.

6 Conclusion

In this work, investigate the Hadley flow analysis of an inclined porous medium with effect of heat source studied by linear stability analysis. The critical value of \(R_{z}\) is studied in the longitudinal rolls, and those are investigated for various combinations of the flow field parameters. It is concluded from the figures that

  • As inclination angle increases, it causes the strong stabilization irrespective of heat source.

  • As heat source increases, it causes the strong destabilization irrespective of inclination angle.

  • It is clear that overall the considerable changes appeared in the \(R_{z}\) subject to inclination angle and heat source.