Keywords

1 Introduction

Over the past several decades, we have enjoyed exponential growth of computational power, namely, Moore’s law. Nowadays even smart phone or tablet PC is much more powerful than super computers in 1980s. People are still seeking more computational power, especially for artificial intelligence (machine learning), chemical and material simulations, and forecasting complex phenomena like economics, weather and climate. In addition to improving computational power of conventional computers, i.e., more Moore’s law, a new generation of computing paradigm has been started to be investigated to go beyond Moore’s law. Among them, natural computing seeks to exploit natural physical or biological systems as computational resource. Quantum reservoir computing is an intersection of two different paradigms of natural computing, namely, quantum computing and reservoir computing.

Regarding quantum computing, the recent rapid experimental progress in controlling complex quantum systems motivates us to use quantum mechanical law as a new principle of information processing, namely, quantum information processing (Nielsen and Chuang 2010; Fujii 2015). For example, certain mathematical problems, such as integer factorisation, which are believed to be intractable on a classical computer, are known to be efficiently solvable by a sophisticatedly synthesized quantum algorithm (Shor 1994). Therefore, considerable experimental effort has been devoted to realizing full-fledged universal quantum computers (Barends et al. 2014; Kelly et al. 2015). In the near feature, quantum computers of size \(>50\) qubits with fidelity \(>99\%\) for each elementary gate would appear to achieve quantum computational supremacy beating simulation on the-state-of-the-art classical supercomputers (Preskill 2018; Boixo et al. 2018). While this does not directly mean that a quantum computer outperforms classical computers for a useful task like machine learning, now applications of such a near-term quantum device for useful tasks including machine learning has been widely explored. On the other hand, quantum simulators (Feynman 1982) are thought to be much easier to implement than a full-fledged universal quantum computer. In this regard, existing quantum simulators have already shed new light on the physics of complex many-body quantum systems (Cirac and Zoller 2012; Bloch et al. 2012; Georgescu et al. 2014), and a restricted class of quantum dynamics, known as adiabatic dynamics, has also been applied to combinatorial optimisation problems (Kadowaki and Nishimori 1998; Farhi et al. 2001; Rønnow et al. 2014; Boixo et al. 2014). However, complex real-time quantum dynamics, which is one of the most difficult tasks for classical computers to simulate  (Morimae et al. 2014; Fujii et al. 2016; Fujii and Tamate 2016) and has great potential to perform nontrivial information processing, is now waiting to be harnessed as a resource for more general purpose information processing.

Physical reservoir computing, which is the main subject throughout this book, is another paradigm for exploiting complex physical systems for information processing. In this framework, the low-dimensional input is projected to a high-dimensional dynamical system, which is typically referred to as a reservoir, generating transient dynamics that facilitates the separation of input states (Rabinovich et al. 2008). If the dynamics of the reservoir involve both adequate memory and nonlinearity (Dambre et al. 2012), emulating nonlinear dynamical systems only requires adding a linear and static readout from the high-dimensional state space of the reservoir. A number of different implementations of reservoirs have been proposed, such as abstract dynamical systems for echo state networks (ESNs) (Jaeger and Haas 2004) or models of neurons for liquid state machines (Maass et al. 2002). The implementations are not limited to programs running on the PC but also include physical systems, such as the surface of water in a laminar state (Fernando and Sojakka 2003), analogue circuits and optoelectronic systems (Appeltant et al. 2011; Woods and Naughton 2012; Larger et al. 2012; Paquot et al. 2012; Brunner et al. 2013; Vandoorne et al. 2014), and neuromorphic chips (Stieg et al. 2012). Recently, it has been reported that the mechanical bodies of soft and compliant robots have also been successfully used as a reservoir (Hauser et al. 2011; Nakajima et al. 2013a, b, 2014, 2015; Caluwaerts et al. 2014). In contrast to the refinements required by learning algorithms, such as in deep learning (LeCun et al. 2015), the approach followed by reservoir computing, especially when applied to real systems, is to find an appropriate form of physics that exhibits rich dynamics, thereby allowing us to outsource a part of the computation.

Quantum reservoir computing (QRC) was born in the marriage of quantum computing and physical reservoir computing above to harness complex quantum dynamics as a reservoir for real-time machine learning tasks (Fujii and Nakajima 2017). Since the idea of QRC has been proposed in Fujii and Nakajima (2017), its proof-of-principle experimental demonstration for non-temporal tasks (Negoro et al. 2018) and performance analysis and improvement (Nakajima et al. 2019; Kutvonen et al. 2020; Tran and Nakajima 2020) has been explored. The QRC approach to quantum tasks such as quantum tomography and quantum state preparation has been recently garnering attention (Ghosh et al. 2019a, b, 2020). In this book chapter, we will provide a broad picture of QRC and related approaches starting from a pedagogical introduction to quantum mechanics and machine learning.

The rest of this paper is organized as follows. In Sect. 2, we will provide a pedagogical introduction to quantum mechanics for those who are not familiar to it and fix our notation. In Sect. 3, we will briefly mention to several machine learning techniques like, linear and nonlinear regressions, temporal machine learning tasks and reservoir computing. In Sect. 4, we will explain QRC and related approaches, quantum extreme learning machine (Negoro et al. 2018) and quantum circuit learning (Mitarai et al. 2018). The former is a framework to use quantum reservoir for non-temporal tasks, that is, the input is fed into a quantum system, and generalization or classification tasks are performed by a linear regression on a quantum enhanced feature space. In the latter, the parameters of the quantum system are further fine-tuned via the gradient descent by measuring an analytically obtained gradient, just like the backpropagation for feedforward neural networks. Regarding QRC, we will also see chaotic time series predictions as demonstrations. Section 5 is devoted to conclusion and discussion.

2 Pedagogical Introduction to Quantum Mechanics

In this section, we would like to provide a pedagogical introduction to how quantum mechanical systems work for those who are not familiar to quantum mechanics. If you already familiar to quantum mechanics and its notations, please skip to Sect. 3.

2.1 Quantum State

A state of a quantum system is described by a state vector,

$$\begin{aligned} |\psi \rangle = \left( \begin{array}{c} c_1 \\ \vdots \\ c_d \end{array} \right) \end{aligned}$$
(1)

on a complex d-dimensional system \(\mathbb {C}^d\), where the symbol \(| \cdot \rangle \) is called ket and indicates a complex column vector. Similarly, \(\langle \cdot |\) is called bra and indicates a complex row vector, and they are related complex conjugate,

$$\begin{aligned} \langle \psi | = |\psi \rangle ^{\dag } = \left( \begin{array}{ccc} c^*_1&\ldots&c^*_d \end{array} \right) . \end{aligned}$$
(2)

With this notation, we can write an inner product of two quantum state \(|\psi \rangle \) and \(|\phi \rangle \) by \(\langle \psi | \phi \rangle \). Let us define an orthogonal basis

$$\begin{aligned} |1\rangle = \left( \begin{array}{c} 1 \\ 0 \\ \vdots \\ \vdots \\ 0 \end{array} \right) ,... \;\;\; |k\rangle = \left( \begin{array}{c} 0 \\ \vdots \\ 1 \\ 0 \\ \vdots \end{array} \right) ,... \;\;\; |d\rangle = \left( \begin{array}{c} 0 \\ \vdots \\ \vdots \\ \vdots \\ d \end{array} \right) , \end{aligned}$$
(3)

a quantum state in the d-dimensional system can be described simply by

$$\begin{aligned} |\psi \rangle = \sum _{i=1}^{d} c_i | i\rangle . \end{aligned}$$
(4)

The state is said to be a superposition state of \(|i\rangle \). The coefficients \(\{c_i\}\) are complex, and called complex probability amplitudes. If we measure the system in the basis \(\{ |i \rangle \}\), we obtain the measurement outcome i with a probability

$$\begin{aligned} p_i = | \langle i | \psi \rangle |^2 = | c_i | ^2 , \end{aligned}$$
(5)

and hence the complex probability amplitudes have to be normalized as follows

$$\begin{aligned} |\langle \psi | \psi \rangle |^2 = \sum _{i=1}^d |c_i|^2 =1. \end{aligned}$$
(6)

In other words, a quantum state is represented as a normalized vector on a complex vector space.

Suppose the measurement outcome i corresponds to a certain physical value \(a_i\), like energy, magnetization and so on, then the expectation value of the physical valuable is given by

$$\begin{aligned} \sum _i a_i p_i = \langle \psi | A |\psi \rangle \equiv \langle A \rangle , \end{aligned}$$
(7)

where we define an hermitian operator

$$\begin{aligned} A = \sum _i a_i |i\rangle \langle i|, \end{aligned}$$
(8)

which is called observable, and has the information of the measurement basis and physical valuable.

The state vector in quantum mechanics is similar to a probability distribution, but essentially different form it, since it is much more primitive; it can take complex value and is more like a square root of a probability. The unique features of the quantum systems come from this property.

2.2 Time Evolution

The time evolution of a quantum system is determined by a Hamiltonian H, which is a hermitian operator acting on the system. Let us denote a quantum state at time \(t=0\) by \(|\psi (0)\rangle \). The equation of motion for quantum mechanics, so-called Schrödinger equation, is given by

$$\begin{aligned} i \frac{\partial }{\partial t} |\psi (t)\rangle = H |\psi (t)\rangle . \end{aligned}$$
(9)

This equation can be formally solved by

$$\begin{aligned} |\psi (t) \rangle = e^{-i H t } |\psi (0)\rangle . \end{aligned}$$
(10)

Therefore, the time evolution is given by an operator \(e^{-i H t}\), which is a unitary operator and hence the norm of the state vector is preserved, meaning the probability conservation. In general, the Hamiltonian can be time dependent. Regarding the time evolution, if you are not interested in the continuous time evolution, but in just its input and output relation, then the time evolution is nothing but a unitary operator U

$$\begin{aligned} |\psi _\mathrm{out} \rangle = U |\psi _\mathrm{in} \rangle . \end{aligned}$$
(11)

In quantum computing, the time evolution U is sometimes called quantum gate.

2.3 Qubits

The smallest nontrivial quantum system is a two-dimensional quantum system \(\mathbb {C}^2\), which is called quantum bit or qubit:

$$\begin{aligned} \alpha |0\rangle + \beta |1\rangle , \;\;\; (|\alpha |^2 + |\beta |^2 = 1). \end{aligned}$$
(12)

Suppose we have n qubits. The n-qubit system is defined by a tensor product space \((\mathbb {C}^2)^{\otimes n}\) of each two-dimensional system as follows. A basis of the system is defined by a direct product of a binary state \(|x_k\rangle \) with \(x_k \in \{ 0,1\}\),

$$\begin{aligned} |x_1 \rangle \otimes | x_2 \rangle \otimes \cdots \otimes |x_n \rangle , \end{aligned}$$
(13)

which is simply denoted by

$$\begin{aligned} |x_1 x_2 \cdots x_n \rangle . \end{aligned}$$
(14)

Then, a state of the n-qubit system can be described as

$$\begin{aligned} |\psi \rangle = \sum _{x_1 ,x_2 ,\ldots ,x_n} \alpha _{x_1 ,x_2, \ldots ,x_n} |x_1 x_2 \cdots x_n \rangle . \end{aligned}$$
(15)

The dimension of the n-qubit system is \(2^n\), and hence the tensor product space is nothing but a \(2^n\)-dimensional complex vector space \(\mathbb {C}^{2^n}\). The dimension of the n-qubit system increases exponentially in the number n of the qubits.

2.4 Density Operator

Next, I would like to introduce operator formalism of the above quantum mechanics. This describes an exactly the same thing but sometimes the operator formalism would be convenient. Let us consider an operator \(\rho \) constructed from the state vector \(|\psi \rangle \):

$$\begin{aligned} \rho = |\psi \rangle \langle \psi |. \end{aligned}$$
(16)

If you chose the basis of the system \(\{ |i \rangle \}\) for the matrix representation, then the diagonal elements of \(\rho \) corresponds the probability distribution \(p_i = |c_i |^2\) when the system is measured in the basis \(\{ |i \rangle \}\). Therefore, the operator \(\rho \) is called a density operator. The probability distribution can also be given in terms of \(\rho \) by

$$\begin{aligned} p_i = \mathrm{Tr}[ |i \rangle \langle i | \rho ], \end{aligned}$$
(17)

where \(\mathrm{Tr}\) is the matrix trace. An expectation value of an observable A is given by

$$\begin{aligned} \langle A \rangle = \mathrm{Tr}[A\rho ]. \end{aligned}$$
(18)

The density operator can handle a more general situation where a quantum state is sampled form a set of quantum states \(\{ |\psi _k \rangle \}\) with a probability distribution \(\{ q_k \}\). In this case, if we measure the system in the basis \(\{ | i\rangle \langle i|\}\), the probability to obtain the measurement outcome i is given by

$$\begin{aligned} p_i = \sum _k q_k \mathrm{Tr}[|i \rangle \langle i | \rho _k], \end{aligned}$$
(19)

where \(\rho _k = | \psi _k \rangle \langle \psi _k |\). By using linearity of the trace function, this reads

$$\begin{aligned} p_i = \mathrm{Tr}[|i \rangle \langle i | \sum _k q_k \rho _k]. \end{aligned}$$
(20)

Now, we interpret that the density operator is given by

$$\begin{aligned} \rho = \sum _k q_k |\psi _k \rangle \langle \psi _k | . \end{aligned}$$
(21)

In this way, a density operator can represent classical mixture of quantum states by a convex mixture of density operators, which is convenient in many cases. In general, a positive and hermitian operator \(\rho \) being subject to \(\mathrm{Tr} [\rho ] = 1\) can be a density operator, since it can be interpreted as a convex mixture of quantum states via spectral decomposition:

$$\begin{aligned} \rho = \sum \lambda _i | \lambda _i \rangle \langle \lambda _i | , \end{aligned}$$
(22)

where \(\{ |\lambda _i \rangle \}\) and \(\{ \lambda _i \}\) are the eigenstates and eigenvectors, respectively. Because of \(\mathrm{Tr}[\rho ] =1\), we have \(\sum _i \lambda _i =1\).

From its definition, the time evolution of \(\rho \) can be given by

$$\begin{aligned} \rho (t) = e^{-i H t} \rho (0) e^{iHt} \end{aligned}$$
(23)

or

$$\begin{aligned} \rho _\mathrm{out} = U \rho _\mathrm{in} U^{\dag }. \end{aligned}$$
(24)

Moreover, we can define more general operations for the density operators. For example, if we apply unitary operators U and V with probabilities p and \((1-p)\), respectively, then we have

$$\begin{aligned} \rho _\mathrm{out} = p U \rho U ^{\dag } + (1-p) V \rho V ^{\dag }. \end{aligned}$$
(25)

As another example, if we perform the measurement of \(\rho \) in the basis \(\{ |i \rangle \}\), and we forget about the measurement outcome, then the state is now given by a density operator

$$\begin{aligned} \sum _i \mathrm{Tr}[|i \rangle \langle i | \rho ] |i \rangle \langle i | = \sum _i |i \rangle \langle i | \rho |i \rangle \langle i |. \end{aligned}$$
(26)

Therefore, if we define a map from a density operator to another, which we call superoperator,

$$\begin{aligned} \mathcal {M} (\cdots ) = \sum _i |i \rangle \langle i | (\cdots ) |i \rangle \langle i |, \end{aligned}$$
(27)

the above non-selective measurement (forgetting about the measurement outcomes) is simply written by

$$\begin{aligned} \mathcal {M} (\rho ). \end{aligned}$$
(28)

In general, any physically allowed quantum operation \(\mathcal {K}\) that maps a density operator to another can be represented in terms of a set of operators \(\{K_i \}\) being subject to \(K_i ^{\dag } K_i = I\) with an identity operator I:

$$\begin{aligned} \mathcal {K}(\rho ) = \sum _i K_i \rho K^{\dag }_i. \end{aligned}$$
(29)

The operators \(\{K_i\}\) are called Kraus operators.

2.5 Vector Representation of Density Operators

Finally, we would like to introduce a vector representation of the above operator formalism. The operators themselves satisfy axioms of the linear space. Moreover, we can also define an inner product for two operators, so-called Hilbert–Schmidt inner product, by

$$\begin{aligned} \mathrm{Tr} [A^{\dag } B ] . \end{aligned}$$
(30)

The operators on the n-qubit system can be spanned by the tensor product of Pauli operators \(\{ I, X, Y,Z\}^{\otimes n}\),

$$\begin{aligned} P({\boldsymbol{i}}) =\bigotimes _{k=1}^{n} \sigma _{i_{2k-1}i_{2k}}. \end{aligned}$$
(31)

where \(\sigma _{ij}\) is the Pauli operators:

$$\begin{aligned} I=\sigma _{00}= \left( \begin{array}{cc} 1 &{} 0 \\ 0 &{} 1 \end{array} \right) , X= \sigma _{10}= \left( \begin{array}{cc} 0 &{} 1 \\ 1 &{} 0 \end{array} \right) , Z=\sigma _{01}= \left( \begin{array}{cc} 1 &{} 0 \\ 0 &{} -1 \end{array} \right) , Y=\sigma _{11}= \left( \begin{array}{cc} 0 &{} -i \\ i &{} 0 \end{array} \right) .\qquad \end{aligned}$$
(32)

Since the Pauli operators constitute a complete basis on the operator space, any operator A can be decomposed into a linear combination of \(P({\boldsymbol{i}})\),

$$\begin{aligned} A = \sum _ {{\boldsymbol{i}}} a_{{\boldsymbol{i}}} P({\boldsymbol{i}}). \end{aligned}$$
(33)

The coefficient \(a_{{\boldsymbol{i}}}\) can be calculated by using the Hilbert–Schmidt inner product as follows:

$$\begin{aligned} a_{{\boldsymbol{i}}} = \mathrm{Tr}[P({\boldsymbol{i}})A]/2^n, \end{aligned}$$
(34)

by virtue of the orthogonality

$$\begin{aligned} \mathrm{Tr} [P({\boldsymbol{i}})P({\boldsymbol{j}})] /2^n = \delta _{{\boldsymbol{i}},{\boldsymbol{j}}}. \end{aligned}$$
(35)

The number of the n-qubit Pauli operators \(\{ P ({\boldsymbol{i}})\}\) is \(4^n\), and hence a density operator \(\rho \) of the n-qubit system can be represented as a \(4^n\)-dimensional vector

$$\begin{aligned} {\boldsymbol{r}} = \left( \begin{array}{c} r_{00\ldots 0} \\ \vdots \\ r_{11\ldots 1} \end{array} \right) , \end{aligned}$$
(36)

where \(r_{00\ldots 0}=1/2^n\) because of \(\mathrm{Tr}[\rho ]=1\). Moreover, because \(P({\boldsymbol{i}})\) is hermitian, \({\boldsymbol{r}}\) is a real vector. The superoperator \(\mathcal {K}\) is a linear map for the operator, and hence can be represented as a matrix acting on the vector \({\boldsymbol{r}}\):

$$\begin{aligned} \rho ' = \mathcal {K}(\rho ) \Leftrightarrow {\boldsymbol{r}}' = K {\boldsymbol{r}}, \end{aligned}$$
(37)

where the matrix element is given by

$$\begin{aligned} K_{{\boldsymbol{i}}{\boldsymbol{j}}} = \mathrm{Tr}[ P({\boldsymbol{i}}) \mathcal {K} \left( P({\boldsymbol{j}}) \right) ]/2^n . \end{aligned}$$
(38)

In this way, a density operator \(\rho \) and a quantum operation \(\mathcal {K}\) on it can be represented by a vector \({\boldsymbol{r}}\) and a matrix K, respectively.

3 Machine Learning and Reservoir Approach

In this section, we briefly introduce machine learning and reservoir approaches.

3.1 Linear and Nonlinear Regression

A supervised machine learning is a task to construct a model f(x) from a given set of teacher data \(\{ x^{(j)},y^{(j)} \}\) and to predict the output of an unknown input x. Suppose x is a d-dimensional data, and f(x) is one dimensional, for simplicity. The simplest model is linear regression, which models f(x) as a linear function with respect to the input:

$$\begin{aligned} f(x) = \sum _{i=1}^{d} w_i x_i + w_0. \end{aligned}$$
(39)

The weights \(\{w_i\}\) and bias \(w_0\) are chosen such that an error between f(x) and the output of the teacher data, i.e. loss, becomes minimum. If we employ a quadratic loss function for given teacher data \( \{ \{x^{(j)}_i\} , y^{(j)}\}\), the problem we have to solve is as follows:

$$\begin{aligned} \min _{\{w_i\}} \sum _j (\sum _{i=0}^{d} w_i x^{(j)}_i - y^{(j)})^2, \end{aligned}$$
(40)

where we introduced a constant node \(x_0 =1\). This corresponds to solving a superimposing equations:

$$\begin{aligned} \mathbf {y} = \mathbf {X} \mathbf {w}, \end{aligned}$$
(41)

where \(\mathbf {y} _j = y^{(j)}\), \(\mathbf {X}_{ji} = x^{(j)}_i\), and \(\mathbf {w}_i = w_i\). This can be solved by using the Moore–Penrose pseudo inverse \(\mathbf {X}^{+}\), which can be defined from the singular value decomposition of \(\mathbf {X} = U D V^{T}\) to be

$$\begin{aligned} \mathbf {X}^{+} = V D U^{T}. \end{aligned}$$
(42)

Unfortunately, the linear regression results in a poor performance in complicated machine learning tasks, and any kind of nonlinearity is essentially required in the model. A neural network is a way to introduce nonlinearity to the model, which is inspired by the human brain. In the neural network, the d-dimensional input data x is fed into N-dimensional hidden nodes with an \(N\times d\) input matrix \(W^\mathrm{in}\):

$$\begin{aligned} W^\mathrm{in} x. \end{aligned}$$
(43)

Then, each element of the hidden nodes is now processed by a nonlinear activation function \(\sigma \) such as \(\tanh \), which is denoted by

$$\begin{aligned} \sigma ( W^\mathrm{in} x). \end{aligned}$$
(44)

Finally, the output is extracted by an output weight \(W^\mathrm{out}\) (\(1 \times N\) dimensional matrix):

$$\begin{aligned} W^\mathrm{out} \sigma ( W^\mathrm{in} x). \end{aligned}$$
(45)

The parameters in \(W^\mathrm{in}\) and \(W^\mathrm{out}\) are trained such that the error between the output and teacher data becomes minimum. While this optimization problem is highly nonlinear, a gradient based optimization, so-called backpropagation, can be employed. To improve a representation power of the model, we can concatenate the linear transformation and the activation function as follows:

$$\begin{aligned} W^\mathrm{out} \sigma \left( W^{(l)} \ldots \sigma \left( W^{(1)} \sigma ( W^\mathrm{in} x) \right) \right) , \end{aligned}$$
(46)

which is called multi-layer perceptron or deep neural network.

3.2 Temporal Task

The above task is not a temporal task, meaning that the input data is not sequential but given simultaneously like the recognition task of images for hand written language, pictures and so on. However, for a recognition of spoken language or prediction of time series like stock market, which are called temporal tasks, the network has to handle the input data that is given in a sequential way. To do so, the recurrent neural network feeds the previous states of the nodes back into the states of the nodes at next step, which allows the network to memorize the past input. In contrast, the neural network without any recurrency is called a feedforward neural network.

Let us formalize a temporal machine learning task with the recurrent neural network. For given input time series \(\{ x_k \}_{k=1}^{L}\) and target time series \(\{ \bar{y}_k \}_{k=1}^{L}\), a temporal machine learning is a task to generalize a nonlinear function,

$$\begin{aligned} \bar{y}_k = f(\{ x_j\}_{j=1}^{k}). \end{aligned}$$
(47)

For simplicity, we consider one-dimensional input and output time series, but their generalization to a multi-dimensional case is straightforward. To learn the nonlinear function \(f(\{ x_j\}_{j=1}^{k})\), the recurrent neural network can be employed as a model. Suppose the recurrent neural network consists of m nodes and is denoted by m-dimensional vector

$$\begin{aligned} {\boldsymbol{r}}=\left( \begin{array}{c} r_1 \\ \vdots \\ r_m \end{array} \right) . \end{aligned}$$
(48)

To process the input time series, the nodes evolve by

$$\begin{aligned} {\boldsymbol{r}}(k+1) = \sigma [W {\boldsymbol{r}}(k) +W^\mathrm{in} x_k], \end{aligned}$$
(49)

where W is an \(m \times m\) transition matrix and \(W^\mathrm{in}\) is an \(m \times 1\) input weight matrix. Nonlinearity comes from the nonlinear function \(\sigma \) applied on each element of the nodes. The output time series from the network is defined in terms of a \(1 \times m\) readout weights by

$$\begin{aligned} y_k = W^\mathrm{out} {\boldsymbol{r}}(k). \end{aligned}$$
(50)

Then, the learning task is to determine the parameters in \(W^\mathrm{in}\), W, and \(W^\mathrm{out}\) by using the teacher data \(\{ x_k , \bar{y}_k \}_{k=1}^{L}\) so as to minimize an error between the teacher \(\{ \bar{y}_k \}\) and the output \(\{ y_k \}\) of the network.

3.3 Reservoir Approach

While the representation power of the recurrent neural network can be improved by increasing the number of the nodes, it makes the optimization process of the weights hard and unstable. Specifically, the backpropagation-based methods always suffer from the vanishing gradient problem. The idea of reservoir computing is to resolve this problem by mapping an input into a complex higher dimensional feature space, i.e., reservoir, and by performing simple linear regression on it.

Let us first see a reservoir approach on a feedforward neural network, which is called extreme learning machine (Huang et al. 2006). The input data x is fed into a network like multi-layer perceptron, where all weights are chosen randomly. The states of the hidden nodes at some layer are now regarded as basis functions of the input x in the feature space:

$$\begin{aligned} \{ \phi _1 (x), \phi _2 (x),\ldots , \phi _N(x)\}. \end{aligned}$$
(51)

Now, the output is defined as a linear combination of these

$$\begin{aligned} \sum _i w_i \phi _i (x) + w_0 \end{aligned}$$
(52)

and hence the coefficients are determined simply by the linear regression as mentioned before. If the dimension and nonlinearity of the the basis functions are high enough, we can model a complex task simply by the linear regression.

The echo state network is similar but employs the reservoir idea for the recurrent neural network (Jaeger and Haas 2004; Maass et al. 2002; Verstraeten et al. 2007), which has been proposed before extreme learning machine appeared. To be specific, the input weights \(W^\mathrm{in}\) and weight matrix W are both chosen randomly up to an appropriate normalization. Then, the learning task is done by finding the readout weights \(W^\mathrm{out}\) to minimize the mean square error

$$\begin{aligned} \sum _{k} (y_k - \bar{y}_k)^2. \end{aligned}$$
(53)

This problem can be solved stably by using the pseudo inverse as we mentioned before.

For both feedforward and recurrent types, the reservoir approach does not need to tune the internal parameters of the network depending on the tasks as long as it posses sufficient complexity. Therefore, the system, to which the machine learning tasks are outsourced, is not necessarily the neural network anymore, but any nonlinear physical system of large degree of freedoms can be employed as a reservoir for information processing, namely, physical reservoir computing (Fernando and Sojakka 2003; Appeltant et al. 2011; Woods and Naughton 2012; Larger et al. 2012; Paquot et al. 2012; Brunner et al. 2013; Vandoorne et al. 2014; Stieg et al. 2012; Hauser et al. 2011; Nakajima et al. 2013a, b, 2014, 2015; Caluwaerts et al. 2014).

4 Quantum Machine Learning on Near-Term Quantum Devices

In this section, we will see QRC and related frameworks for quantum machine learning. Before going deep into the temporal tasks done on QRC, we first explain how complicated quantum natural dynamics can be exploit as generalization and classification tasks. This can be viewed as a quantum version of extreme learning machine (Negoro et al. 2018). While it is an opposite direction to reservoir computing, we will also see quantum circuit learning (QCL) (Mitarai et al. 2018), where the parameters in the complex dynamics is further tuned in addition to the linear readout weights. QCL is a quantum version of a feedforward neural network. Finally, we will explain quantum reservoir computing by extending quantum extreme learning machine for temporal learning tasks.

4.1 Quantum Extreme Learning Machine

The idea of quantum extreme learning machine lies in using a Hilbert space, where quantum states live, as an enhanced feature space of the input data. Let us denote the set of input and teacher data by \(\{ x^{(j)}, \bar{y}^{(j)} \}\). Suppose we have an n-qubit system, which is initialized to

$$\begin{aligned} |0\rangle ^{\otimes n}. \end{aligned}$$
(54)

In order to feed the input data into quantum system, a unitary operation parameterized by x, say V(x), is applied on the initial state:

$$\begin{aligned} V(x)|0\rangle ^{\otimes n}. \end{aligned}$$
(55)

For example, if x is one-dimensional data and normalized to be \(0 \le x \le 1\), then we may employ the Y-basis rotation \(e^{-i \theta Y}\) with an angle \(\theta = \arccos (\sqrt{x})\):

$$\begin{aligned} e^{-i \theta Y} |0\rangle = \sqrt{x} |0\rangle + \sqrt{1-x} |1\rangle . \end{aligned}$$
(56)

The expectation value of Z with respect to \(e^{-i \theta Y} |0\rangle \) becomes

$$\begin{aligned} \langle Z \rangle = 2x -1, \end{aligned}$$
(57)

and hence is linearly related to the input x. To enhance the power of quantum enhanced feature space, the input could be transformed by using a nonlinear function \(\phi \):

$$\begin{aligned} \theta = \arccos (\sqrt{\phi (x)}). \end{aligned}$$
(58)

The nonlinear function \(\phi \) could be, for example, hyperbolic tangent, Legendre polynomial, and so on. For simplicity, below we will use the simple linear input \(\theta = \arccos (\sqrt{x})\).

If we apply the same operation on each of the n qubits, we have

$$\begin{aligned} V(x) |0\rangle ^{\otimes n}= & {} (\sqrt{x} |0\rangle + \sqrt{1-x} |1\rangle )^{\otimes n} \nonumber \\= & {} (1-x)^{n/2} \sum _{i_1,\ldots ,i_n} \prod _k \sqrt{ \frac{x}{1-x} }^{i_k} |i_1,\ldots ,i_n\rangle . \end{aligned}$$
(59)

Therefore, we have coefficients that are nonlinear with respect to the input x because of the tensor product structure. Still the expectation value of the single-qubit operator \(Z_k\) on the kth qubit is \(2x-1\). However, if we measure a correlated operator like \(Z_1 Z_2\), we can obtain a second-order nonlinear output

$$\begin{aligned} \langle Z_1 Z_2 \rangle = (2x-1)^2 \end{aligned}$$
(60)

with respect to the input x. To measure a correlated operator, it is enough to apply an entangling unitary operation like CNOT gate \(\Lambda (X)=|0\rangle \langle 0| \otimes I + |1\rangle \langle 1| \otimes X\):

$$\begin{aligned} \langle \psi | \Lambda _{1,2}(X) Z_1 \Lambda _{1,2}(X) |\psi \rangle = \langle \psi | Z_1 Z_2 | \psi \rangle . \end{aligned}$$
(61)

In general, an n-qubit unitary operation U transforms the observable Z under the conjugation into a linear combination of Pauli operators:

$$\begin{aligned} U^{\dag } Z_1 U = \sum _{{\boldsymbol{i}}} \alpha _{{\boldsymbol{i}}} P({\boldsymbol{i}}). \end{aligned}$$
(62)

Thus if you measure the output of the quantum circuit after applying a unitary operation U,

$$\begin{aligned} U V(x) |0\rangle ^{\otimes n}, \end{aligned}$$
(63)

you can get a complex nonlinear output, which could be represented as a linear combination of exponentially many nonlinear functions. U should be chosen to be appropriately complex with keeping experimental feasibility but not necessarily fine-tuned.

Fig. 1
figure 1

The expectation value \(\langle Z \rangle \) of the output of a quantum circuit as a function of the input \((x_0,x_1)\)

Full size image

To see how the output behaves in a nonlinear way with respect to the input, in Fig. 1, we will plot the output \(\langle Z \rangle \) for the input \((x_0,x_1)\) and \(n=8\), where the inputs are fed into the quantum state by the Y-rotation with angles

$$\begin{aligned} \theta _{2k} = k \arccos (\sqrt{x_0}) \end{aligned}$$
(64)
$$\begin{aligned} \theta _{2k+1} = k \arccos (\sqrt{x_1}) \end{aligned}$$
(65)

on the 2kth and \((2k+1)\)th qubits, respectively. Regarding the unitary operation U, random two-qubit gates are sequentially applied on any pairs of two qubits on the 8-qubit system.

Suppose the Pauli Z operator is measured on each qubit as an observable. Then, we have

$$\begin{aligned} z_i = \langle Z_i \rangle , \end{aligned}$$
(66)

for each qubit. In quantum extreme learning machine, the output is defined by taking linear combination of these n output:

$$\begin{aligned} y = \sum _{i=1}^{n} w_i z_i . \end{aligned}$$
(67)

Now, the linear readout weights \(\{ w_i \}\) are tuned so that the quadratic loss function

$$\begin{aligned} L = \sum _j (y^{(j)}- \bar{y}^{(j)})^2 \end{aligned}$$
(68)

becomes minimum. As we mentioned previously, this can be solved by using the pseudo inverse. In short, quantum extreme learning machine is a linear regression on a randomly chosen nonlinear basis functions, which come from the quantum state in a space of an exponentially large dimension, namely quantum enhanced feature space. Furthermore, under some typical nonlinear function and unitary operations settings to transform the observables, the output in Eq. (67) can approximate any continuous function of the input. This property is known as the universal approximation property (UAP), which implies that the quantum extreme learning machine can handle a wide class of machine learning tasks with at least the same power as the classical extreme learning machine (Goto et al. 2020).

Here we should note that a similar approach, quantum kernel estimation, has been taken in Havlicek et al. (2019) and Kusumoto et al. (2021). In quantum extreme learning machine, a classical feature vector \( \phi _i(x) \equiv \langle \Phi (x) |Z_i | \Phi (x) \rangle \) is extracted from observables on the quantum feature space \(|\Phi (x) \rangle \equiv V(x)|0\rangle ^{\otimes n}\). Then, linear regression is taken by using the classical feature vector. On the other hand, in quantum kernel estimation, quantum feature space is fully employed by using support vector machine with the kernel functions \(K(x,x') \equiv \langle \Phi (x) | \Phi (x') \rangle \), which can be estimated on a quantum computer. While classification power would be better for quantum kernel estimation, it requires more quantum computational costs both for learning and prediction in contrast to quantum extreme learning machine.

Fig. 2
figure 2

a The quantum circuit for quantum extreme learning machine. The box with \(theta _k\) indicates Y-rotations by angles \(\theta _k\). The red and blue boxes correspond to X and Z rotations by random angles, Each dotted-line box represents a two-qubit gate consisting of two controlled-Z gates and 8 X-rotations and 4 Z-rotations. As denoted by the dashed-line box, the sequence of the 7 dotted boxes is repeated twice. The readout is defined by a linear combination of \(\langle Z_i \rangle \) with constant bias term 1.0 and the input \((x_0,x_1)\). b (Left) The training data for a two-class classification problem. (Middle) The readout after learning. (Right) Prediction from the readout with threshold at 0.5

Full size image

In Fig. 2,we demonstrate quantum extreme learning machine for a two-class classification task of a two-dimensional input \(0\le x_0, x_1 \le 1\). Class 0 and 1 are defined to be those being subject to \((x_0 -0.5)^2 + (x_1-0.5)^2 \le 0.15\) and \(>0.15\), respectively. The linear readout weights \(\{ w_i\}\) are learned with 1000 randomly chosen training data and prediction is performed with 1000 randomly chosen inputs. The class 0 and 1 are determined whether or not the output y is larger than 0.5. Quantum extreme learning machine with an 8-qubit quantum circuit shown in Fig. 2a succeeds to predict the class with \(95\%\) accuracy. On the other hand, a simple linear regression for \((x_0,x_1)\) results in \(39\%\). Moreover, quantum extreme learning machine with \(U=I\), meaning no entangling gate, also results in poor, \(42\%\). In this way, the feature space enhanced by quantum entangling operations is important to obtain a good performance in quantum extreme learning machine.

4.2 Quantum Circuit Learning

In the split of reservoir computing, dynamics of a physical system is not fine-tuned but natural dynamics of the system is harnessed for machine learning tasks. However, if we see the-state-of-the-art quantum computing devices, the parameter of quantum operations can be finely tuned as done for universal quantum computing. Therefore, it is natural to extend quantum extreme learning machine by tuning the parameters in the quantum circuit just like feedfoward neural networks with backpropagation.

Using parameterized quantum circuits for supervised machine leaning tasks such as generalization of nonlinear functions and pattern recognitions have been proposed in Mitarai et al. (2018), Farhi and Neven (2018), which we call quantum circuit learning. Let us consider the same situation with quantum extreme learning machine. The state before the measurement is given by

$$\begin{aligned} UV(x) |0\rangle ^{\otimes n}. \end{aligned}$$
(69)

In the case of quantum extreme learning machine, the unitary operation for a nonlinear transformation with respect to the input parameter x is randomly chosen. However, the unitary operation U may also be parameterized:

$$\begin{aligned} U(\{ \phi _k \}) = \prod _{k} u( \phi _k ). \end{aligned}$$
(70)

Thereby, the output from the quantum circuit with respect to an observable A

$$\begin{aligned} \langle A (\{ \phi _k\},x) \rangle = \langle 0|^{\otimes n} V^{\dag }(x) U(\{ \phi _k \})^{\dag } Z_i U(\{ \phi _k \})V(x) |0 \rangle ^{\otimes n} \end{aligned}$$
(71)

becomes a function of the circuit parameters \(\{ \phi _k\}\) in addition to the input x. Then, the parameters \(\{ \phi _k\}\) are tuned so as to minimize the error between teacher data and the output, for example, by using the gradient just like the output of the feedforward neural network.

Let us define a teacher dataset \(\{ x^{(j)}, y^{(j)}\}\) and a quadratic loss function

$$\begin{aligned} L(\{ \phi _k\}) = \sum _j (\langle A (\{ \phi _k\},x^{(j)}) \rangle - y^{(j)})^2. \end{aligned}$$
(72)

The gradient of the loss function can be obtained as follows:

$$\begin{aligned} \frac{\partial }{\partial \phi _l } L(\{ \phi _k\})= & {} \frac{\partial }{\partial \phi _l } \sum _j (\langle A (\{ \phi _k\},x^{(j)}) \rangle - y^{(j)})^2 \end{aligned}$$
(73)
$$\begin{aligned}= & {} \sum _j 2(\langle A (\{ \phi _k\},x^{(j)}) \rangle - y^{(j)}) \frac{\partial }{\partial \phi _l } \langle A (\{ \phi _k\},x^{(j)}) \rangle . \end{aligned}$$
(74)

Therefore, if we can measure the gradient of the observable \(\langle A (\{ \phi _k\},x^{(j)}) \rangle \), the loss function can be minimized according to the gradient descent.

If the unitary operation \(u(\phi _k)\) is given by

$$\begin{aligned} u(\phi _k) = W_k e^{-i (\phi _k/2) P_k}, \end{aligned}$$
(75)

where \(W_k\) is an arbitrary unitary, and \(P_k\) is a Pauli operator. Then, the partial derivative with respect to the lth parameter can be analytically calculated from the outputs \(\langle A (\{ \phi _k\},x^{(j)}) \rangle \) with shifting the lth parameter by \(\pm \epsilon \) (Mitarai et al. 2018; Mitarai and Fujii 2019):

$$\begin{aligned}&\frac{\partial }{\partial \phi _l } \langle A (\{ \phi _k\},x^{(j)}) \rangle \nonumber \\= & {} \frac{1}{2 \sin \epsilon } ( \langle A (\{ \phi _1 ,\ldots , \phi _l + \epsilon , \phi _{l+1},\ldots \},x^{(j)}) \rangle - \langle A (\{ \phi _1 ,\ldots , \phi _l - \epsilon , \phi _{l+1},\ldots \},x^{(j)}) \rangle ). \nonumber \\&\end{aligned}$$
(76)

By considering the statistical error to measure the observable \(\langle A \rangle \), \(\epsilon \) should be chosen to be \(\epsilon = \pi /2\) so as to make the denominator maximum. After measuring the partial derivatives for all parameters \(\phi _k\) and calculating the gradient of the loss function \(L(\{ \phi _k\})\), the parameters are now updated by the gradient descent:

$$\begin{aligned} \theta _l ^{(m+1)} = \theta _l ^{(m)} - \alpha \frac{\partial }{\partial \phi _l} L(\{ \phi _k\}). \end{aligned}$$
(77)

The idea of using the parameterized quantum circuits for machine learning is now widespread. After the proposal of quantum circuit learning based on the analytical gradient estimation above (Mitarai et al. 2018) and a similar idea (Farhi and Neven 2018), several researches have been performed with various types of parameterized quantum circuits (Schuld et al. 2020; Huggins et al. 2019; Chen et al. 2018; Glasser et al. 2018; Du et al. 2018) and various models and types of machine learning including generative models (Benedetti et al. 2019a; Liu and Wang 2018) and generative adversarial models (Benedetti et al. 2019b; Situ et al. 2020; Zeng et al. 2019; Romero and Aspuru-Guzik 2019). Moreover, an expression power of the parameterized quantum circuits and its advantage against classical probabilistic models have been investigated (Du et al. 2020). Experimentally feasible ways to measure an analytical gradient of the parameterized quantum circuits have been investigated (Mitarai and Fujii 2019; Schuld et al. 2019; Vidal and Theis 2018). An advantage of using such a gradient for the parameter optimization has been also argued in a simple setting (Harrow and John 2019), while the parameter tuning becomes difficult because of the vanishing gradient by an exponentially large Hilbert space (McClean et al. 2018). Software libraries for optimizing parameterized quantum circuits are now developing  (Bergholm et al. 2018; Chen et al. 2019). Quantum machine learning on near-term devices, especially for quantum optical systems, is proposed in Steinbrecher et al. (2019), Killoran et al. (2019). Quantum circuit learning with parameterized quantum circuits has been already experimentally demonstrated on superconducting qubit systems (Havlicek et al. 2019; Wilson et al. 2018) and a trapped ion system (Zhu et al. 2019).

4.3 Quantum Reservoir Computing

Now, we return to the reservoir approach and extend quantum extreme learning machine from non-temporal tasks to temporal ones, namely, quantum reservoir computing (Fujii and Nakajima 2017). We consider a temporal task, which we explained in Sect. 3.2. The input is given by a time series \(\{ x_k\}_{k}^{L}\) and the purpose is to learn a nonlinear temporal function:

$$\begin{aligned} \bar{y}_k = f(\{ x_j \}_{j}^{k}). \end{aligned}$$
(78)

To this end, the target time series \(\{ \bar{y}_k \}_{k=1}^{L}\) is also provided as teacher.

Contrast to the previous setting with non-temporal tasks, we have to fed input into a quantum system sequentially. This requires us to perform an initialization process during computation, and hence the quantum state of the system becomes mixed state. Therefore, in the formulation of QRC, we will use the vector representation of density operators, which was explained in Sect. 2.5.

In the vector representation of density operators, the quantum state of an N-qubit system is given by a vector in a \(4^N\)-dimensional real vector space, \({\boldsymbol{r}} \in \mathbb {R}^{4^N}\). In QRC, similarly to recurrent neural networks, each element of the \(4^N\)-dimensional vector is regarded as a hidden node of the network. As we seen in Sect. 2.5, any physical operation can be written as a linear transformation of the real vector by a \(4^N \times 4^N\) matrix W:

$$\begin{aligned} {\boldsymbol{r}}' = W {\boldsymbol{r}}. \end{aligned}$$
(79)

Now we see, from Eq. (79), a time evolution similar to the recurrent neural network, \({\boldsymbol{r}}' = \tanh ( W {\boldsymbol{r}} )\). However, there is no nonlinearity such as \(\tanh \) in each quantum operation W. Instead, the time evolution W can be changed according to the external input \(x_k\), namely \(W_{x_k}\), which contrasts to the conventional recurrent neural network where the input is fed additively \(W {\boldsymbol{r}} + W^\mathrm{in} x_k\). This allows the quantum reservoir to process the input information \(\{x_k\}\) nonlinearly, by repetitively feeding the input.

Fig. 3
figure 3

a Quantum reservoir computing. b Virtual nodes and temporal multiplexing

Full size image

Suppose the input \(\{ x_k\}\) is normalized such that \(0 \le x_k \le 1\). As an input, we replace a part of the qubits to the quantum state. The density operator is given by

$$\begin{aligned} \rho _{x_k} = \frac{I+(2 x_k - 1)Z}{2}. \end{aligned}$$
(80)

For simplicity, below we consider the case where only one qubit is replaced for the input. Corresponding matrix \(S_{x_k}\) is given by

$$\begin{aligned} (S_{x_k})_{{\boldsymbol{j}}{\boldsymbol{i}}} = \mathrm{Tr}\left\{ P({\boldsymbol{j}}) \frac{I+(2x_k-1)Z}{2} \otimes \mathrm{Tr}_\mathrm{replace} [P({\boldsymbol{i}})] \right\} /2^N, \end{aligned}$$
(81)

where \(\mathrm{Tr}_\mathrm{replace}\) indicates a partial trace with respect to the replaced qubit. With this definition, we have

$$\begin{aligned} \rho ' = \mathrm{Tr}_\mathrm{replace}[\rho ] \otimes \rho _{x_k} \Leftrightarrow {\boldsymbol{r}}' = S_{x_k} {\boldsymbol{r}}. \end{aligned}$$
(82)

The unitary time evolution, which is necessary to obtain a nonlinear behavior with respect to the input valuable \(x_k\), is taken as a Hamiltonian dynamics \(e^{-i H \tau }\) for a given time interval \(\tau \). Let us denote its representation on the vector space by \(U_\tau \):

$$\begin{aligned} \rho ' = e^{-i H \tau } \rho e^{i H \tau } \Leftrightarrow {\boldsymbol{r}}' = U_{\tau } {\boldsymbol{r}}. \end{aligned}$$
(83)

Then, a unit time step is written as an input-depending linear transformation:

$$\begin{aligned} {\boldsymbol{r}}((k+1)\tau ) = U_\tau S_{x_k} {\boldsymbol{r}}(k\tau ). \end{aligned}$$
(84)

where \({\boldsymbol{r}}(k\tau )\) indicates the hidden nodes at time \(k\tau \).

Since the number of the hidden nodes are exponentially large, it is not feasible to observe all nodes from experiments. Instead, a set of observed nodes \(\{\bar{r}_l\}_{l=1}^{M}\), which we call true nodes, is defined by a \(M \times 4^N \) matrix R,

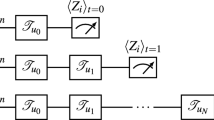
$$\begin{aligned} \bar{r}_l (k\tau ) = \sum _{{\boldsymbol{i}}} R_{l{\boldsymbol{i}}} r_{{\boldsymbol{i}}}(k\tau ). \end{aligned}$$
(85)

The number of true nodes M has to be a polynomial in the number of qubits N. That is, from exponentially many hidden nodes, a polynomial number of true nodes are obtained to define the output from QR (see Fig. 3a):

$$\begin{aligned} y_k = \sum _l W^\mathrm{out}_l \bar{r}_l (k\tau ), \end{aligned}$$
(86)

where \(W_\mathrm{out}\) is the readout weights, which is obtained by using the training data. For simplicity, we take the single-qubit Pauli Z operator on each qubit as the true nodes, i.e.,

$$\begin{aligned} \bar{r}_l = \mathrm{Tr}[Z_l \rho ], \end{aligned}$$
(87)

so that if there is no dynamics these nodes simply provide a linear output \((2x_k -1)\) with respect to the input \(x_k\).

Moreover, in order to improve the performance we also perform the temporal multiplexing. The temporal multiplexing has been found to be useful to extract complex dynamics on the exponentially large hidden nodes through the restricted number of the true nodes (Fujii and Nakajima 2017). In temporal multiplexing, not only the true nodes just after the time evolution \(U_\tau \), also at each of the subdivided V time intervals during the unitary evolution \(U_{\tau }\) to construct V virtual nodes, as shown in Fig. 3b. After each input by \(S_{x_k}\), the signals from the hidden nodes (via the true nodes) are measured for each subdivided intervals after the time evolution by \(U_{ v \tau /V}\) (\(v=1,2,\ldots V\)), i.e.,

$$\begin{aligned} {\boldsymbol{r}}(k\tau +(v/V)\tau ) \equiv U_{(v/V)\tau } S_{x_{k}} {\boldsymbol{r}}(k\tau ). \end{aligned}$$
(88)

In total, now we have \(N \times V\) nodes, and the output is defined as their linear combination:

$$\begin{aligned} y_k = \sum _{l=1}^{N} \sum _{v=1}^{V} W^\mathrm{out}_{j,v} \bar{r}_{l}(k\tau +(v/V)\tau ). \end{aligned}$$
(89)

By using the teacher data \(\{ \bar{y}_k \}_{k}^{L}\), the linear readout weights \(W^\mathrm{out}_{j,v}\) can be determined by using the pseudo inverse. In Fujii and Nakajima (2017), the performance of QRC has been investigated extensively for both binary and continuous inputs. The result shows that even if the number of the qubits are small like 5–7 qubits the performance as powerful as the echo state network of the 100–500 nodes have been reported both in short term memory and parity check capacities. Note that, although we do not go into detail in this chapter, the technique called spatial multiplexing (Nakajima et al. 2019), which exploits multiple quantum reservoirs with common input sequence injected, is also introduced to harness quantum dynamics as a computational resource. Recently, QRC has been further investigated in Kutvonen et al. (2020), Ghosh et al. (2019a), Chen and Nurdin (2019). Specifically, in Ghosh et al. (2019a), the authors use quantum reservoir computing to detect many-body entanglement by estimating nonlinear functions of density operators like entropy.

4.4 Emulating Chaotic Attractors Using Quantum Dynamics

To see a performance of QRC, here we demonstrate an emulation of chaotic attractors. Suppose \(\{ x_k\}_k^{L}\) is a discretized time sequence being subject to a complex nonlinear equation, which might has a chaotic behavior. In this task, the target, which the network is to output, is defined to be

$$\begin{aligned} \bar{y}_{k} = x_{k+1} = f(\{x_{j}\}_{j=1}^{k}). \end{aligned}$$
(90)

That is, the system learns the input of the next step. Once the system successfully learns \(\bar{y}_{k}\), by feeding the output into the input of the next step of the system, the system evolves autonomously.

Fig. 4
figure 4

Demonstrations of chaotic attractor emulations. a Lorenz attractor. b Mackey–Glass system. c Rössler attractor. d Hénon map. The dotted line shows the time step when the system is switched from teacher forced state to autonomous state. In the right side, delayed phase diagrams of learned dynamics are shown

Full size image

Here, we employ the following target time series from chaotic attractors: (i) Lorenz attractor,

$$\begin{aligned} \frac{dx}{dt}= & {} a (y-x), \end{aligned}$$
(91)
$$\begin{aligned} \frac{dy}{dt}= & {} x (b-z) - y, \end{aligned}$$
(92)
$$\begin{aligned} \frac{dz}{dt}= & {} xy - cz, \end{aligned}$$
(93)

with \((a,b,c)=(10,28,8/3)\), (ii) the chaotic attractor of Mackey–Glass equation,

$$\begin{aligned} \frac{d}{dt} x(t) = \beta \frac{x(t-\tau )}{1+x(t-\tau )^n} - \gamma x(t) \end{aligned}$$
(94)

with \((\beta , \gamma , n) = (0.2, 0.1 , 10)\) and \(\tau = 17\), (iii) Rössler attoractor,

$$\begin{aligned} \frac{dx}{dt}= & {} -y-z, \end{aligned}$$
(95)
$$\begin{aligned} \frac{dy}{dt}= & {} x+ay, \end{aligned}$$
(96)
$$\begin{aligned} \frac{dz}{dt}= & {} b+z(x-c), \end{aligned}$$
(97)

with (0.2, 0.2, 5.7), and (iv) Hénon map,

$$\begin{aligned} x_{t+1} = 1-1.4x_t +0.3x_{t-1}. \end{aligned}$$
(98)

Regarding (i)-(iii), the time series is obtained by using the fourth-order Runge–Kutta method with step size 0.02, and only x(t) is employed as a target. For the time evolution of quantum reservoir, we employ a fully connected transverse-field Ising model

$$\begin{aligned} H = \sum _{ij} J_{ij} X_i X_j + h Z_i, \end{aligned}$$
(99)

where the coupling strengths are randomly chosen such that \(J_{ij}\) is distributed randomly from \([-0.5,0.5]\) and \(h=1.0\). The time interval and the number of the virtual nodes are chosen to be \(\tau = 4.0\) and \(v=10\) so as to obtain the best performance. The first \(10^4\) steps are used for training. After the linear readout weights are determined, several \(10^3\) steps are predicted by autonomously evolving the quantum reservoir. The results are shown in Fig. 4 for each of (a) Lorenz attractor, (b) the chaotic attractor of Mackey–Glass system, (c) Rössler attractor, and (d) Hénon map. All these results show that training is done well and the prediction is successful for several hundreds steps. Moreover, the output from the quantum reservoir also successfully reconstruct the structures of these chaotic attractors as you can see from the delayed phase diagram.

5 Conclusion and Discussion

Here, we reviewed quantum reservoir computing and related approaches, quantum extreme learning machine and quantum circuit learning. The idea of quantum reservoir computing comes from the spirit of reservoir computing, i.e., outsourcing information processing to natural physical systems. This idea is best suited to quantum machine learning on near-term quantum devices in noisy intermediate quantum (NISQ) era. Since reservoir computing uses complex physical systems as a feature space to construct a model by the simple linear regression, this approach would be a good way to understand the power of a quantum enhanced feature space.