Keywords

1 Introduction

Variability in manufacturing process and production is inevitable. Assembling parts are known as mating parts. There are two mating parts in a radial assembly, namely male and female parts. However, in a complex radial assembly, more than one hole or shaft can be present. In this study, a hole (male) and a shaft (female) are considered. For interchangeable manufacturing, mating parts are assembled in random order, which results in their clearance variation being the sum of tolerances of both parts. Optimization is done for finding the best grouping of selective assembly. In order to minimize the clearance variation conventionally, manufacturing tolerances needed to be reduced by improving the process or the machine. Therefore, selective assembly is considered to be the best possible method for obtaining minimum clearance variation, as it is economical and quite simple.

Mansoor [15] categorized and minimized the problem of mismatching for selective assembly. Pugh [17] recommended a methodology for segregating population from the mating parts. Pugh [18] presented a technique to shortlist components having large variance. He identified and analyzed the effects of three sources of error produced while applying this method. Fang and Zhang [3] proposed an algorithm by introducing two prerequisite principles to match probabilities of mating parts. They found an effective approach to avoid the unforeseen loss of production cost. This method is appropriate when the required clearance is more than the difference in standard deviations of parts. Chan and Linn [1] developed method for grouping the parts having dissimilar distribution to ensure that mating parts’ probability is equal to the equivalent groups maintaining dimensional constraints. It also minimizes the production of excess parts and uses another concept of skipping certain portions of shafts or holes so that more mating groups can be made.

Kannan and Jayabalan [4] analyzed a ball bearing assembly with three mating parts (inner race, ball, and outer race) and suggested a method of grouping complex assemblies to minimize excess parts and to satisfy the clearance requirements. Kannan and Jayabalan [5] investigated linear assembly having three parts and suggested method for finding smaller assembly variations having minimum excessive parts. Kannan et al. [7] proposed two methods (uniform grouping and equal probability) to achieve group tolerances which are uniform and to avoid surplus parts in method 1. The group tolerances are designed such that they satisfy the clearance requirements, and the excess parts are minimalized in method 2. Kannan et al. [6] have used GA to select the best combination to minimize the clearance variation and excess parts when the parts are assembled linearly for selective assembly.

This paper is arranged as follows: Section 2 provides the details about mathematical model of selective assembly system that has been used for optimization. Section 3 provides the framework of CI algorithm. Section 4 comprises of the results and discussion that are obtained by optimization of selective assembly. Conclusion and the future scope are given in Sect. 5.

2 Selective Assembly System

Selective assembly is a cost-effective approach to attaining necessary clearance variation in the resultant assembled product from the low precision elements. More often, due to manufacturing limitations and errors, the individual elements have high tolerance limits. Clearance is the difference in the dimensions of the elements. Clearance is one of the zenith priorities for the determination of the quality of the output product. The mating parts characteristically have different standard deviations as a virtue of their manufacturing processes. When from these elements, high-precision assemblies need to be manufactured, and the concept of selective assembly is adopted. The most important benefit of this concept is the low-cost association with the process.

Pugh [17] proposed the idea of partitioning the universal set of the mating part population into a number of groups. Generally, the mating parts include a female part and a male part (hole and shaft respectively in this case). After the creation of groups of these parts, assembly is done by the combination of these individual groups, thereby reducing the overall clearance variation of the assembly. It is a known fact that the actual manufactured product dimensions generally have a normal distribution with the standard deviation of 6σ. However, for very high-precision applications like aerospace. 8σ may also be used [6].

For minimizing clearance variation and reducing computational time, a new system of selective assembly is proposed here to solve the problem of hole and shaft assemblies. Instead of assembling corresponding groups, different combinations of the selective groups are assembled, and the best combination is found using CI.

Each of the groups will have a specific tolerance corresponding to them for female and male elements. The mathematical formulation of the desired clearance is provided below:

$$ \begin{aligned} {\text{Max}}. \,{\text{Clearance}} & = \left( {N \times \left( {{\text{Group}}\,{\text{clearance}}\,{\text{width}}\,{\text{of}}\,{\text{hole}}} \right)} \right) \\ & \quad + \left( {M \times \left( {{\text{Group}}\,{\text{clearance}}\,{\text{width}}\,{\text{of}}\,{\text{shaft}}} \right)} \right) \\ \end{aligned} $$
(1)
$$ \begin{aligned} {\text{Min}}. \,{\text{Clearance}} & = \left( {\left( {N - 1} \right) \times \left( {{\text{Group}}\,{\text{clearance}}\,{\text{width}}\,{\text{of}}\,{\text{hole}}} \right)} \right) \\ & \quad + \left( {\left( {M - 1} \right) \times \left( {{\text{Group}}\,{\text{clearance}}\,{\text{width}}\,{\text{of}}\,{\text{shaft}}} \right)} \right) \\ \end{aligned} $$
(2)
$$ {\text{Overall}}\,{\text{Clearance}} = {\text{Max}}.\,{\text{Clearance}} - {\text{Min}}.\,{\text{Clearance}} $$
(3)

where N represents the group number of the hole used for combining and M represents the group number of the shaft used for combining, for example, for group 3:

$$ {\text{Max}}.\,{\text{Clearance}} = \left( {3 \times 2} \right) + \left( {3 \times 3} \right) = 15 $$
(4)
$$ {\text{Min}}. \,{\text{Clearance}} = \left( {2 \times 2} \right) + \left( {2 \times 3} \right) = 10 $$
(5)

Similarly, we find the remaining clearance ranges as follows:

Group 1—5 mm; group 2—10 mm; group 3—15 mm; group 4—20 mm; group 5—25 mm; group 6—30 mm.

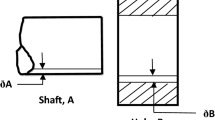
In selective assembly (refer to Fig. 1), the groups made can be assembled interchangeably [6] (i.e., first group of holes may be assembled with fifth group of shafts). In our case, we have considered six group categorization and group width of 3 and 2 mm for hole and shaft, respectively.

Fig. 1
figure 1

Traditional method of selective assembly

Full size image

3 Cohort Intelligence Algorithm

Cohort intelligence is a recent ramification of artificial intelligence. The algorithm is inspired from the behavior of self-supervised candidates such as natural and social tendency in cohort, which was represented in Kulkarni et al. [13]. The algorithm refers to learning of self-supervised behavior of candidates in a cohort and adapts to behavior of other candidates, which it intends to follow. In this, interaction of candidates takes place, which helps the candidates to learn from one another. The candidates update/improve their behavior, ultimately improving behavior of entire candidates in cohort by embracing qualities of other candidates. Roulette wheel approach is used for the selection of candidate to be followed, interact, and compete with. This in turn allows the candidates to follow candidates having either best or worst behavior. The convergence of candidates in cohort takes place when all the candidates reach to the optimal solution using the above technique. The detailed procedure of CI algorithm can be found in Dhavle et al. [2] and Kulkarni et al. [13].

Krishnasamy et al. [8] have used a data clustering, hybrid evolutionary algorithm combining K-mean and modified cohort intelligence. In UCI Machine Learning Repository, various data sets were considered and its performances were noted down. Using hybrid K-MCI, they were able to achieve promising results having quality solutions and good convergence speed. Kulkarni et al. [9, 11] proposed and applied metaheuristic of CI to two constraint handling approaches, namely static (SCI) and dynamic (DCI) penalty functions. Also, mechanical engineering domain-related three real-world problems were also improved to obtain optimal solution. The robustness and applicability of CI were compared with the help of different nature-inspired optimization algorithm. CI has recently been applied to fractional proportional-integral-derivative (PID) controller parameters. Shah et al. [20] designed the fractional PID controller with the help of CI method and compared the validation of the result with the help of existing algorithms such as PSO, improved electromagnetic algorithm, and GA, in which best cost function, function evaluation, and computational time in comparison with other algorithms, which inherently demonstrated the robustness of CI method in control domain also, is yielded. Patankar and Kulkarni [16] proposed seven variations of CI and validated for three uni-modal unconstraint and seven multimodal test functions. This analysis instigated the strategy for working in a cohort. The choice of the right variation may also further opens doors for CI to solve different real-world problems. Shastri et al. [21] used CI approach for solving probability-based constrained handling approach and some inequality-based constrained handling problems. CI was found to be highly efficient by comparing its performance for robustness, computational time, and various static parameters and its further usage in solving more real-world problems. Kulkarni and Shabir [12] have applied CI to solve NP-hard combinatorial problem, in which the problem was successfully solved showing its efficiency and improved rate of convergence. Hence, it has also been used to solve some combinatorial problems. Dhavle et al. [2] applied the CI method for optimal design and inherently reducing the total cost of the shell and tube heat exchanger. Promising results were obtained for all the three cases, which were considered for optimizing the total cost of the complex design of STHE and obtaining least computational time and function evaluation in comparison with other algorithms, showing its applicability and robustness for different complex systems in mechanical engineering domain. Sarmah and Kulkarni [19] applied CI in two steganographic techniques, which use JPEG compression on gray scale image to hide secret text. In this, CI provides good result, in comparison with other algorithms, and reveals the hidden secret text. Kulkarni et al. [10] have applied CI algorithm to various problems such as travelling salesman problem, sea cargo mix problem, and cross-border shippers problem. The flowchart of the CI algorithm applying for selective assembly is given in Fig. 2.

Fig. 2
figure 2

Flowchart for application of CI to selective assembly

Full size image

4 Results and Discussions

Two methods were used to obtain the optimized clearance variance. One was adopting CI while using roulette wheel (Table 1), and the other was without using the roulette wheel (Table 2). For comparison, four cases are considered for each method, and these four cases included variation in the number of candidates that are 5, 10, 15, and 20. The number of iterations is kept 500 as constant throughout the study. The algorithm code was written in MATLAB R2016b running on Windows 10 operating system using Intel Core i3, 2.7 GHz processor with 4 GB of RAM.

Table 1 Using roulette wheel concept
Full size table
Table 2 Without roulette wheel concept
Full size table

In the case of non-roulette wheel, the candidates follow the best-performing candidate. In case their performance does not improve, the candidate goes back to its original behavior; i.e., if the updated combination of the candidate yields worse clearance behavior, it goes back to its original combination. However, in the case of using roulette wheel, there are no criteria to follow the best-performing candidate. Therefore, we may get a lower value of clearance variation in one solution, but because of randomization, the next solution may tend to increase the clearance variation value. In spite of this, convergence is achieved fairly faster than before and is highly reliable for higher number of candidates. Please note that the element of a candidate to be changed are randomised in both cases.

In case of using the roulette wheel, we can see that in Fig. 3, the initial value of minimum clearance variation is 19. However, because of no limiting criteria and randomization, this value shoots up and down before converging at the lowest possible value of 10.

Fig. 3
figure 3

Graph depicting minimum value of clearance variation for each iteration using roulette wheel for 20 candidates and 200 iterations

Full size image

In the case of not using the roulette wheel, we can see that in Fig. 4, the initial value of minimum clearance variation is 21. However, because the algorithm follows the best-performing candidate, we see that the solution improves with each successive iteration and converges at the lowest possible value of 10. Moreover, because of this, the convergence is achieved in lesser number of iterations. We can clearly infer from the tables and the figures that as we keep on increasing the number of candidates, we tend to get a near-perfect value of clearance variation at convergence. One of the primary reasons for this occurrence is that the solution depends on having a candidate with low clearance variation in the initial set. Because of randomization, the chances of getting this are lower if you have lower number of candidates. Therefore, as we keep on increasing the number of candidates, the chances of having a lower clearance variation candidate increases, hence improving our overall solution. However, in reality, we will be solving this model with hundreds or thousands of candidates, therefore making it a very reliable tool to use.

Fig. 4
figure 4

Graph depicting minimum value of clearance variation for each iteration without using roulette wheel for 20 candidates and 100 iterations

Full size image

5 Conclusion and Future Scope

Two variations of cohort intelligence are used to obtain the optimized clearance variation. It is noteworthy that this minimum clearance is a function of group width of both, male and female mating elements of the assembly. This is better than interchangeable assembly, as in that case, it is the sum of both tolerances which will always be greater than the solution obtained by this method. One of the most important aspects of this method is the extent up to which it curbs the computational time. It was also observed that on increasing the number of candidates, premature convergence is avoided, thus resulting in better outputs showing the robustness of CI algorithm. In the future, algorithms can be modified to achieve optimal solution using lesser number of candidates. This method can further be extended for linear selective assemblies. Also, further variations of CI can be applied to solve similar problems.