1 Introduction

Citizens today are immersed in data, and as a result, promoting statistical literacy has become a fundamental responsibility. Many school curricula have introduced statistics and probability courses to help students become competent in everyday decision-making regarding data. This literacy involves being able to read and interpret data in tables, graphs and summaries, and being able to use such tools to make arguments that include evidence of their validity (Ben-Zvi & Garfield, 2004). In order for a citizen to participate in democratic society in an informed manner, the early and progressive development of abilities with graphs is necessary. This includes the reading, writing and interpretation of graphical representations. Statistical literacy gives a person the ability to critically interpret and evaluate information, surveys and statistics studies appearing in media coverage, as well as to appreciate the value of statistics in everyday life, civic life and professional life as consumers of data (del Pino & Estrella, 2012).

In this chapter, we look at the challenging process of representing (modelling) for pupils in the first years of school. This involves exploration of a set of raw data before they then go on to build their own representations to reveal and provide evidence of the behaviour of the data, its patterns and relationships.

2 Background

2.1 Statistical Literacy

The ideas of Cobb and Moore (1997) have been repeated many times in statistics education, particularly the notions that “data are not just numbers, they are numbers with a context” (p. 801) and “in data analysis, context provides meaning” (p. 803). We believe that data are the centre of statistics and they must, therefore, occupy the same position in school statistics teaching and learning. In order to achieve meaningful statistics instruction, the students must learn about and develop data sense, i.e. a certain numerical sense within a context that provides meaning.

Working with problems and data in context is an opportunity to build authentic literacy and to begin to cement statistics thinking, as expressed by Pfannkuch and Wild (2000). The introduction of exploratory data analysis (EDA) (Tukey, 1977) changed the teaching paradigm for statistics learning, because, as opposed to simply answering set questions, it proposed more flexible and exploratory analysis in search of what can be found in the data. EDA applies methods and ideas needed to organise, represent and describe data, using visual representations such as tables, diagrams, graphs and others, as well as numerical summaries.

It takes time to develop statistical ideas linked to this literacy, and it is therefore advisable to begin in the first years of school (English, 2010, 2013; Franklin & Garfield, 2006; Shaughnessy, 2006). Several research studies into statistics education have looked at graphical representations (e.g. Aoyama, 2007; Estrella, Olfos, Morales, & Vidal-Szabó, 2017; Friel, Curcio, & Bright, 2001; Pérez-Echeverría, Martí, & Pozo, 2010), proposing exploratory data analysis as an effective focus for gaining literacy in this area (e.g. Ben-Zvi & Arcavi, 2001; Ben-Zvi & Garfield, 2004; Burgess, 2011; Estrella & Olfos, 2013; National Council of Teacher of Mathematics [NCTM], 2000, 2009; Shaughnessy, 2006). Regarding graphical representations, Pfannkuch and Wild (2004) believe that even simpler tools such as statistical graphs can be considered statistical models, since they are a statistical way to represent and think about reality.

2.2 Representations in Statistics Education

Chilean primary school curricula suggest that students should be able to argue and discuss solutions they present to certain problems, supporting their reasoning with the use of different ways to communicate their ideas, including representations (Chilean Ministry of Education [MINEDUC], 2012). The mathematics curriculum states that students should be able to use a wide variety of representations and apply them fluidly. However, this requirement limits students’ learning to simply using and reproducing pictorial representations, such as diagrams, figures and graphs, to communicate (MINEDUC, 2012). As with many primary school curricula, it fails to consider the production of original and unique representations by the students themselves.

Our perspective aims to revitalise the spirit of EDA to place focus on original representations that emerge from decisions made by the students in search of better comprehension of how data behave, which is not necessarily achieved with representations from standardised school reproductions established by the curriculum. Statistics learning includes opportunities to select methods to graph and analyse data, and in statistics, the choice of how to analyse the data is equally (if not more) important than the accounts and calculations used to carry out the procedure (Garfield & Franklin, 2011, p. 136). Very few studies explore students’ interactions with different representations (e.g. Estrella et al., 2017; Martí, 2009; Pérez-Echevarría, & Scheurer, 2009), although the interpretation and construction of representations can lead to better comprehension of statistical concepts (Duval, 1995; Tippett, 2016). This lack of attention on how to work with representation in schools can limit students’ learning regarding representation (diSessa, 2004).

There is very little systematic research that looks at the role of the signs that comprise a representation built by students (e.g. Earnest, 2015; English, 2012; Estrella et al., 2017; Martí, 2009). Research into students with a high level of understanding of the number line and of the structure of a rectangular grid shows that they possess the capacity to acquire graphical abilities quicker than others (Mulligan, Mitchelmore, English, & Crevensten, 2013). Therefore, it is necessary to document, describe and classify the models and representations students use, as well as the explanations they give for their statistical ideas as solution alternatives for a given problem that requires data management. Hence, a contribution to the area of statistics education would be to provide evidence of the components of data representation and thus demonstrate the improved understanding of the behaviour of data shown by some students in the representations they build.

2.3 Reading and Building Our Own Representations

The process of deciding what to do with a set of data in order to understand its behaviour is critical. Reading previously constructed data representations has been studied (e.g. Curcio, 1987; Shaugnessy, Garfield, & Greer, 1996), but there are few studies on the creation of data representations (either typical or invented) and the complexity of building them.

The following section describes some concepts that support our teaching proposal and its aim to develop statistical thinking: meta-representational competence (MRC), some components of representation, transnumeration, statistical thinking and data sense.

3 Conceptual Framework

3.1 Meta-Representational Competence

MRC describes the complete range of abilities that a subject possesses to be able to build and use external representations (diSessa, 2004; diSessa & Sherin, 2000). It includes the ability to select, produce and use representations constructively, and to criticise and modify, understand and explain and even design new representations (see Table 14.1).

Table 14.1 Aspects of meta-representational competence
Full size table

MRC recognises the native ability of students to create their own representations, an ability that is gradually developed through cultural practices inside and outside the classroom. MRC also identifies two main categories of native ability in students: first, a wide range of resources to design representations, including perceptual attributes, such as length, size, numerosity, colour and second, judgement of the representation. The term representational competence covers a wide range of activities involved in representing, while the prefix “meta” is added in order to avoid limiting the term to typical representations or those taught in school as methods of reproduction.

3.2 Some Components of Representations

In the construction of data representations, coordination among statistical, numerical and geometric components associated with data organisation is activated. These are assumed to have been built on mathematics abilities in the early development of the students. The ability to represent requires coordination between geometric and numerical quantities (Duval, 2014; Earnest, 2015; Estrella et al., 2017).

As a component of statistical structure, the concept “variable” crosses all areas of statistics and is central to data representations and their behaviour. A variable is understood as any measurable characteristic of a set of individuals that can take different values and can be categorised.

As a component of numerical structure, “frequency” is the cardinal number corresponding to each category of a variable. When part of a representation, it is aligned with other frequencies, but separated from the qualitative variable. Therefore, in determining absolute frequency it is necessary to obtain the cardinal number for the whole set. Through understanding the principle of cardinality, students can relate sets of different sizes depending on their quantity.

Estrella, Olfos, Vidal-Szabô, Morales and Estrella (2018) define some components of geometric structure in a graphical data representation, including base-line, linearity-graph and unit-of-equal-size. The first establishes the base on which the data representation is placed and then built. The second allows comparison of heights or ordered distribution over a physical space, and the last gives the visual equivalency between each data point. Specifically, the base-line component is the base given by a line (either explicit or implicit) on which the data organisation begins in order for the representation to then be built, and linearity-graph is the linearity characteristic of data organisation into columns or rows, in which unit-of-equal-size is simultaneously respected along with the conservation of the space between each unit of data represented. These components are essential for comparing and visualising a relationship among the data.

3.3 Transnumeration

This is a type of statistical thinking that is carried out when beginning a process of transforming data into a representation or changing a representation or coordination of representations, with the intention of gaining better understanding (Pfannkuch & Wild, 2004). This dynamic process involves interpreting the information received from the data representations, returning to the context to make assertions, answering questions or asking new ones. The transnumeration process comprises transnumeration techniques, such as creating a new variable, changing the type of variable, organising the data differently or representing it visually, sorting data, forming groups, graphing a graph or table, calculating central tendency or measure of the spread, calculating frequencies, selecting and analysing a subset of the data (Chick, 2003).

3.4 Statistical Thinking

This is a way of thinking that involves the inductive reasoning common to statistical processes (e.g. identification of data patterns). This type of thinking includes generalisation through the relationships between covariant quantities (e.g. correlation), the representation of these relationships in different ways using natural language, symbolic expressions, tables and graphs, and fluid reasoning between representations to interpret and predict the behaviour of functions (Blanton, Levi, Crites, & Dougherty, 2011).

3.5 Data Sense

This conceptual framework ends with the notion of data sense, which we have built and presented based on the idea of numerical sense reviewed by Berch (2005). Therefore, the proposed elements of data sense come from key ideas and techniques common in statistical processes (Burrill & Biehler, 2011). They include the ability to do the following:

  1. 1.

    Approximate or estimate based on data behaviour.

  2. 2.

    Make data comparisons of numerical magnitude in different data representations.

  3. 3.

    Use numbers and quantitative methods to communicate, process and interpret information from the data and from contextual knowledge.

  4. 4.

    Recognise the need for data, searching for links between the new information and prior conceptual knowledge.

  5. 5.

    Understand numbers in context as reference points for measuring variability in the uncertain real world.

  6. 6.

    Move seamlessly between real-world quantities and the world of statistical data.

  7. 7.

    Represent data units in multiple ways depending on the context and the aim of the data representation, moving between different representations to gain a better understanding of the behaviour of the data and to make predictions beyond the data.

  8. 8.

    Think or speak in a sensible manner about the behaviour of the data in a statistical problem, without making any precise calculations.

  9. 9.

    Recognise research as a statistical process that includes a problem, plan, data collection, data analysis and drawing of conclusions, using the data as evidence.

  10. 10.

    Be aware that a research process is taking place with a real experience with data and the understanding of statistical concepts, using everyday decision-making.

4 Methodology

4.1 Participants and Context

This study details the experiences of five pupils who attend the same Chilean school, and whose performance is average. Three are preschool pupils, 5 years old, (from a class with 27 pupils) and two are primary pupils, 7 years old, (from a class of 38 pupils). The pupils experienced an open-ended data organisation lesson without prior instruction. Both lessons were designed by teachers at their school (one group of four preschool teachers and another group of second grade 4) during eight sessions carried out at the school and mediated by four researchers. The researchers asked the teachers to participate in a course on school-level statistics through lesson study (Estrella, Mena-Lorca, & Olfos, 2018; Isoda, Arcavi, & Mena, 2007; Isoda & Olfos, 2009) and to promote the connection between theory and practice in statistics education.

4.2 Statistics Lesson Design by Teachers in Lesson Study

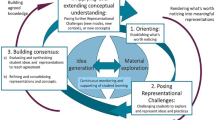
Figure 14.1 shows the lesson study cycle as formulated and used by the groups of teachers. They worked together to formulate their considerations regarding learning statistics and made professional decisions in order to design their lesson plan.

Fig. 14.1
figure 1

Lesson study cycle implemented for statistics

Full size image

We then analysed the representations built by the pupils with pen and paper when performing an open data organisation task with categorical variables (grade K: “the class’s favourite sports activities”; and grade 2: “water consumption in the home”), including some video-recorded transcriptions of pupil interviews. After describing and analysing the cases, students’ MRC is studied based on the representations, transnumeration techniques used in the statistical process, the data sense and the components demonstrated in the representations.

The cases presented here were selected to answer the central statistics question of each lesson, respectively, due to the richness of the productions made by the pupils while completing the lesson, and their degree of participation when expressing their ideas during the lesson and in the interview.

5 Statistics Lessons in Preschool and School

5.1 Preschool Lesson (Three Preschool Pupils)

A group of teachers of grade K developed a lesson with a theme that would be interesting to the children. The pupils were asked about their favourite sports activity with the idea that the most popular answer would then be organised for the children during one of their break times. This group met for 120 min a week for two months. They planned a lesson and implemented it on three occasions, improving it each time in terms of the teaching for their students’ statistics learning. The teachers were involved in a research cycle (Wild & Pfannkuch, 1999) known as Problem, Plan, Data, Analysis and Conclusions (PPDAC). They experienced the entire statistical process and took it to the classroom in order for their pupils to then conduct the same cycle in a statistics learning setting using the EDA paradigm (Ben-Zvi, 2016), applying real data from the school context. The central question of the statistics lesson was: What is our class’s favourite sports activity?

  • Grade K Cases: Juan, José and Maria

The data representation performed by the pupils of grade K contained two critical moments.

Moment 1: The pupils gave evidence of categorisation of the variables (the class’s favourite sports activity) and therefore, of implicit comprehension of the concept of variable, by showing in their data representation six activities classified by type (jumping, running, skating, bike-riding, playing basketball and playing football).

Moment 2: After observing the presentation of the representations of their classmates, three pupils showed their data representation to the class, and one of them, on his own initiative, asked for a pencil and wrote down the cardinal number of each categorised activity, thus answering the questions of the statistics task regarding the class’s favourite sports activity.

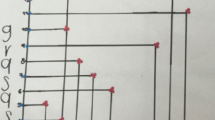
The pupils demonstrated understanding of the statistics component variable and its categorisation. However, the geometric component was less developed, since the data were cut out in different sizes and shapes, and not all were placed on the same base-line (see third category in Fig. 14.2). For this grade, the subsequent emergence of the numerical component was notable. In this case, it was the frequency of the variable, and in the answer, the pupil not only stated the cardinal number “10”, but also the context, “the favourite activity is bike-riding”.

Fig. 14.2
figure 2

Preschool pupils’ data representation, and the moment they calculated and recorded frequency

Full size image

At several times, the pupils applied transnumeration techniques (see grey boxes in Fig. 14.3), by ordering the data and grouping them to represent them, creating a new variable (frequency) and analysing a subset of the data.

Fig. 14.3
figure 3

Suggested components of data sense and transnumeration techniques in the task of representing data performed by three preschool children

Full size image

The preschool pupils participated in a lesson that allowed them to build the categories of the variable, absolute frequency, functionally, and to use subitizing and counting strategies (see Figs. 14.2 and 14.3). This learning experience allowed them to develop their data sense, as the pupils were able to express their ideas on the behaviour of the data without making precise calculations (Moment 1) and to demonstrate their ability to use numbers and cardination to communicate and process the data in order to obtain information from their contextual knowledge (Moment 2).

With regard to MRC, this group of pupils demonstrated the aspects of invention and learning, as they created and designed their own representations. The learning aspect was shown at the moment when the pupils became aware of their own understanding of the data representation they had built and of the usefulness of absolute frequency to answer the central question.

5.2 Second Grade Lesson (Two Pupils)

The group of four grade 2 teachers designed and studied an open-ended problem lesson related to water consumption in the home. These teachers met for 120 min a week for two months. They discussed and planned the lesson, implementing it over three sessions, as with the grade K lesson.

The statistical situation proposed by the four teachers focused on the question: How can we organise data to help reduce water consumption in the home? The teachers chose real data on the daily water consumption of a Chilean family. The data were given to the students in a worksheet with 36 icons, each representing 1 L of water consumption for a typical family (13 toilets, 10 showers, 8 bathroom sinks, 4 kitchen sinks and 1 garden hose). The students produced different representations of the 36 given data points to answer the central question.

The teachers were involved in the entire statistical process of the PPDAC, which they took to the classroom with the objective that the students would perform the same cycle in an EDA setting and reason with data in a familiar context, such as caring for water use.

  • The Second Grade Cases: Julia and Her Diagram of Data Lists with Frequency

In the organisation and representation produced by Julia (see Fig. 14.4), it can be seen that the construction process she employed began by her choosing and counting of the icons on water consumption (data) given on the worksheet. She then wrote a word related to the icon and drew a square around it. She then wrote “- 13” (i.e. a dash and the number 13) on the square with the word and drew 13 icons and then another border around them. Based on this, we can interpret that Julia counted and classified the icons to identify and write the category of the variable and the cardinal number. She repeated this procedure for the remaining data in an unusual order (in the west) from right to left.

Fig. 14.4
figure 4

Diagram of data lists in the process of being built

Full size image

In Julia’s representation, see Fig. 14.4, it can be seen that she organised the data by separating the quantitative from the qualitative. She built vertical lists with repeating icons characterised by: conservation of unity (icons of similar sizes); linearity-graph use in the bars (vertical lists of icons); and base-line (on which the sign of the categorical variable is written with its cardinal number and the bars).

Julia was interviewed and asked about some of her actions and the characteristics of her representation (see Fig. 14.5). She creatively invented a diagram of the data with frequencies and applied her judgement to the representation she built, thus demonstrating the four aspects of MRC: invention, criticism, functionality and learning (Table 14.1). The decisions Julia took in building her data representation allowed her to compare the data lists and reach correct conclusions based on the relationship of the variable category to its frequency, stating that the use of the highest form of water consumption should be restricted, i.e. the variable category with the highest frequency.

Fig. 14.5
figure 5

Suggested components of data sense and transnumeration techniques in the task of representing data performed by Julia, grade 2

Full size image

  • Manuel and His Absolute Frequency Table

Figure 14.6 shows a different representation produced by Manuel, which is a horizontal table comprised of a rectangle with two rows and five columns. The upper cells show the icons that represent the variable categories, and the lower cells show cardinal numbers for each category, i.e. the absolute frequencies.

Fig. 14.6
figure 6

Icon table of absolute frequencies created by Manuel

Full size image

In the process of building his data representation, Manuel outlined an upper segment and from this drew the cells, filling each with a drawn icon (the categorical variable) and below this he wrote the corresponding cardinal number. This procedure was repeated for each category, drawing a representative icon and thus demonstrating a certain linearity-graph aspect of the cells (verticality of the iconic lists).

Manuel classified the data belonging to the same category of a set of data presented in iconic form and then searched for a relationship that would allow him to answer the question. By observing the repeated data icons, he saw that there was a representative of them for each category of the variable and he expressed this by drawing a single icon. Each iconic data symbol represented a category of the variable, and each category was placed on the header upper of the horizontal table of absolute frequencies.

The context of water use awareness gave meaning to the variable “water consumption” and to the categories that emerged, which were visualised as classes (categories of the variable) and ordered horizontally in the table of frequencies (see Fig. 14.6).

In the interview, Manuel indicated understanding of the tabular data representation as a tool that allowed him to simultaneously verify the cardinal value and the frequency without having to count again. By inventing this data representation, Manuel moved away from the individual data point and presented an (aggregated) global summary, and he recognised the situation context and the functionality of his table of frequencies corresponding to this, thus providing indications of strong MRC, i.e. all the aspects (invention, criticism, functionality and learning) described in Table 14.1. The number sense within the context is articulated with data sense that emerges from the representation used in his discourse to communicate (see Fig. 14.7).

Fig. 14.7
figure 7

Suggested components of data sense and transnumeration techniques in the task of representing data performed by Manuel, grade 2

Full size image

5.3 The Role of the Teacher in Statistics Lessons

In lessons with open problems as proposed by both groups of teachers (preschool and grade 2), it was the pupils who spoke, thought, questioned and built answers; they argued, communicated and discussed with their peers. The role of the teacher was to encourage the pupils to listen to each other, to take an interest in the questions posed by their classmates and to make an effort to understand the presentations they constructed and the underlying statistical concepts they used.

By implementing the PPDAC research cycle in an EDA setting, the teachers experienced the entire statistical process and were therefore aware of the challenge facing the pupils. There were some groups of pupils who initially used the data as drawings without any meaning and who could not understand the complexity of the data organisation, as they had not comprehended the contextual meaning of the data (specifically, 21 of the 27 pre-schoolers, and 8 of the 38 2nd-graders). However, in the end they joined the majority of the groups who presented and were able to detect patterns, irregular questions and trends. In order to induce statistical thinking, the teachers conversed with the groups of pupils, promoting criticism, exploration and visualisation of the behaviour of the data, as they had planned, and thus bringing the pupils’ emerging statistics ideas into play.

6 Conclusions

The first years of school provide an ideal setting for promoting statistics, not only due to the importance of the subject in several different domains of modern society, but also because it reinforces understanding of various mathematical concepts (e.g. numbers, measurement, counting, cardinals, partitions, classification, operations, even distribution, sorting, etc.), while at the same time integrating students into a context in order to awaken the development of their statistical thinking.

Through the products of grade K and grade 2 pupils, we have found evidence of essential components in data representations and of increased understanding of data behaviour acquired by the pupils when freely building their own representations. They used graphs and tables, moving from individual data points to aggregated data. This gave them the opportunity to attain deeper understanding of the characteristics of a data set and its relationships, through individual data manipulation.

The teachers proposed the objective of developing statistics reasoning and not simply learning specific graphical representations, aiming to develop a certain data sense, encouraging the pupils to see the data representations as a whole instead of individually (moving from individual data points to aggregated data).

The experience of preparing lessons as a group allowed the teachers to experience the entire statistical process and then repeat the biggest part of this process with their pupils. This research process included specification of the problem and the central question of the research, data collection, data analysis, data representation, interpretation and discussion of the results, and communication of the conclusions. The pupils then ordered, classified and organised the data, observing that the data vary and detecting the behaviour of most of the data within the context.

In the specific cases described above, there is notable richness in the graph and table meta-representations created by the pupils. Only a few of the pupils, while talking with their classmates, made links between the cardinal numbers and the context (frequency of the associated variable) or between the iconised data and the context (unit-of-equal-size); either this, or they separated the qualitative (categories of the variable) from the quantitative aspects and used the cardinal linearly (frequency). We believe that this shows that the pupils can develop data sense, as the cardinal number gives meaning within context. They demonstrated an interest in the variable, observing its behaviour through the representations they built, and they made sure the icons were of a similar size, spacing them out homogenously, thus allowing comparison between the categories of the variable that emerged from the initial classification. These cases demonstrated the aspects of MRC, transnumeration techniques in action, and the data sense the pupils were developing.

7 Projections and Opportunities

Recently, in statistics education systematic research has begun into statistical reasoning in the first years of pre-school, primary school and secondary school. Several questions have arisen in the field of early statistics, providing new opportunities for research and action from a focus on teachers and teacher trainers, such as the following:

  • Which new demands for statistics teaching are teacher trainers, teachers and first grade pupils facing?

  • How can early statistic thinking be developed progressively in children?

  • What type of teaching promotes early conceptual understanding and attitude comprehension in statistics?

  • Does interdisciplinary lesson study promote effective lessons for thinking statistically?

  • How does the written curriculum allow early move of EDA to informal statistical inference (ISI)?

  • How can data sense that provides statistical literacy be promoted from early infancy?

  • These questions require further research.