Keywords

1 Introduction

Lightweight composite materials are well established in aerospace sector, water transportation, manufacture of high-end cars, bioengineering, composite bridges to name a few. These materials owing to their high strength/stiffness to weight ratio are also being used in repair and rehabilitation works in civil engineering field. The stability of these structures is one of the important parameters to be considered while designing these structures. Bucking phenomenon is critical since it not only affects a particular structural component, but also its neighbouring components as well. Investigation of the whole structure is time-consuming, and hence, small structural components are studied simulating the actual phenomenon. Laminated composite curved panels which are one of the major shell structural components made up of composite materials are studied in this paper. The study is focused on nonlinear dynamic buckling of laminated composite curved panels.

It is noted that the dynamic buckling analysis is carried out for thin-walled plate structures which are subjected to compressive loads by Kubiak [1]. The laminated composite curved panels are subjected to in-plane dynamic compressive loads in many instances. The pulse loads can be characterised as sinusoidal, triangular, rectangular, exponential, etc. The current study is restricted to rectangular loads. Linearised equations for anisotropic, laminated, and sandwich cylindrical shell panels are proposed by Sciuva and Carrera [2]. These cylindrical panels are subjected to normal and uniform shear forces. Analytical and finite element displacement approaches are used to develop approximate solution for elastic stability. The dynamic buckling behaviour of thermo-viscoplastic circular shells is studied by Wei et al. [3]. The analysis is carried out both analytically as well as using finite element method. The authors have developed algebraic equations for maximum initial growth rate for small disturbance. Finite element method is used to study the effect of initial imperfections in cylindrical shells which are subjected to low-velocity impacts. Rahman et al. [4] have developed a finite element method for imperfection-sensitive shell structures in order to implement a reduction method for dynamic buckling. The approach is based on Budiansky’s approach by incorporating inertial forces. The dynamic buckling of stiffened composite cylindrical shells is studied by Patel et al. [5]. The analysis is carried out using finite element software—ABAQUS/Explicit. The model generated is validated using experimental results of collapse test, and the dynamic buckling analysis is carried out. Priyadarsini et al. [6] investigated the experimental and numerical aspects of dynamic buckling of advanced fibre composite cylindrical shells which are subjected to axial compression. Significant work is taken up by Jensen [7] in the study of parametric excitation, where the pulsating loads act on the structures [8]. Some dynamic buckling criteria available in the literature are Volmir’s criterion, Budiansky–Hutchinson criterion, Ari-Gur and Simonetta’s criterion, Petry–Fahlbusch criterion [1]. In the current study, Volmir’s criterion is used to calculate the dynamic buckling loads. According to this criterion, the critical deflection value is assumed to be equal to the thickness of plate.

2 Theory and Formulation

The nonlinear dynamic equilibrium equation solved by ABAQUS/Explicit is given in Eq. (1).

$$ \left[ M \right]\left\{ {\ddot{u}} \right\} + \left[ C \right]\left\{ {\dot{u}} \right\} + \left[ {K\left( {\left\{ u \right\}} \right)} \right]\left\{ u \right\} = \left\{ {F\left( t \right)} \right\} $$
(1)

where [M] is the mass matrix, [C] the damping matrix, [K] the stiffness matrix, which depends on the deformations due to the geometric nonlinearity, {u} the nodal displacement vector, \( \left\{ {\dot{u}} \right\} \) the nodal velocity vector, \( \left\{ {\ddot{u}} \right\} \) the nodal acceleration vector, and {F(t)} the load vector. In the current study, the damping effect is not considered. The nonlinear dynamic equilibrium equation solved is shown in Eq. (2).

$$ \left[ M \right]\left\{ {\ddot{u}} \right\} + \left[ {K\left( {\left\{ u \right\}} \right)} \right]\left\{ u \right\} = \left\{ {F\left( t \right)} \right\} $$
(2)

3 Results and Discussion

The convergence and validation study is carried out using some of the results reported in the literature. Then, the current problem is then discussed.

3.1 Validation and Convergence

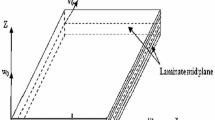
Non-dimensional buckling load is evaluated for a square planed, simply supported, uniformly loaded symmetric cross-ply panel (0°/90°/0°/90°/0°) as shown in Fig. 1. The support conditions are shown in Fig. 2. The material properties and other parameters are taken as: a/b = 1, R/a = 20, a/h = 100, E11 = 40E22, G12 = G13 = 0.5E22, G23 = 0.6E22, and ν12 = 0.25. The non-dimensional buckling load is calculated as, \( \overline{{P_{\text{cr}} }} \) = Pcrb2/E22h3. Table 1 shows the non-dimensional static buckling load for the curved panel along with finite element analysis results presented by Sciuva and Carrera [2] and Patel et al. [8].

Fig. 1
figure 1

Geometry of panel with uniform loading

Full size image
Fig. 2
figure 2

Model showing the support conditions

Full size image
Table 1 Non-dimensional static buckling load
Full size table

The buckling analysis is performed by taking different mesh sizes of the panel. The results with 40 × 40 mesh size match well with the results of Sciuva and Carrera [2] and Patel et al. [8] as shown in Table 1. The same mesh size is taken of dynamic buckling analysis.

3.2 Dynamic Buckling

After the static buckling study, the dynamic buckling analysis is carried out for the same panel used for validation. The pulse loads are the loads having a finite duration. These loads can be a trigonometric, exponential, triangular, etc., functions. In the current study, only rectangular loads are taken into consideration. Figure 3 shows the rectangular loading function taken into consideration for this study. For a particular loading duration, the magnitude of loads is varied and the response is observed. In order to perform dynamic analysis, the material properties presented by Priyadarsini et al. [6] are used. E22 = 9250 MPa and density = 1700 kg/m3. The value of E22 is substituted in the ratios used for the validation study. Table 2 shows the predicted nonlinear dynamic buckling loads.

Fig. 3
figure 3

Rectangular pulse load

Full size image
Table 2 Dynamic buckling loads for laminated composite curved panel
Full size table

Figure 4a–e shows the axial displacement vs time plots for calculating the dynamic buckling load for a loading duration of 0.055 × 10−3 s. For various magnitudes of loads, axial displacement responses are observed. The loads are applied for 0.055 × 10−3 s, and the responses are observed till 0.5 s. The target axial displacement is set in accordance with Volmir’s criterion as the value of thickness = 1 cm, as prescribed by Kubiak [1]. The load which gives a displacement equal to or almost reaches the target value is the dynamic buckling load according to Volmir’s criterion.

Fig. 4
figure 4

a Axial displacement versus time plot of loading duration of 0.055 × 10−3 s. b Axial displacement versus time plot of loading duration of 0.055 × 10−3 s. c Axial displacement versus time plot of loading duration of 0.055 × 10−3 s. d Axial displacement versus time plot of loading duration of 0.055 × 10−3 s. e Axial displacement versus time plot of loading duration of 0.055 × 10−3 s

Full size image

It is observed from Table 2 that in very short duration (0.055 ms), the dynamic buckling load is higher than static buckling load. However, as the loading duration is increased, the dynamic buckling load starts decreasing.

3.2.1 Effect of Aspect Ratio

The effect of aspect ratio is studied on laminated composite curved panel in this section. The ratio b/a is increased keeping a constant and nonlinear dynamic buckling loads are calculated. The pulse loads are applied for various duration. Tables 3, 4, 5, 6, 7, and 8 show the dynamic buckling loads for laminated composite curved panels with different aspect ratios and various loading duration.

Table 3 Dynamic buckling load for 0.1 × 10−3 s
Full size table
Table 4 Dynamic buckling load for 1 × 10−3 s
Full size table
Table 5 Dynamic buckling load for 2.5 × 10−3 s
Full size table
Table 6 Dynamic buckling load for 5 × 10−3 s
Full size table
Table 7 Dynamic buckling load for 7.5 × 10−3 s
Full size table
Table 8 Dynamic buckling load for 10 × 10−3 s
Full size table

Figure 5 shows the effect of aspect ratio on the nonlinear dynamic buckling load of laminated curved panel. It is observed that as the loading duration is increased, the variation of dynamic buckling load is not appreciable. Although for very short durations, 0.1 ms and 1 ms, there is an initial increase in dynamic buckling load, which gradually dissipates as the aspect ratio is increased. Figure 6 shows the deformed shape of the laminated composite curved panel with aspect ratio 2 at point of loading and deformation scale factor = 5.

Fig. 5
figure 5

Effect of aspect ratio on dynamic buckling load

Full size image
Fig. 6
figure 6

Deformed shape of laminated composite curved panel with b/a = 2 and R/a = 20

Full size image

3.2.2 Effect of Radius of Curvature

The effect of radius of curvature is studied on nonlinear dynamic buckling behaviour of laminated composite curved panel in this section. The ratio R/a is varied along with loading duration. For each loading duration, the dynamic buckling loads are calculated.

Figure 7 shows the effect of radius of curvature on nonlinear dynamic buckling behaviour of laminated composite curved panel. It is seen that for a particular loading duration, the variation of dynamic buckling load is less. The variation of dynamic buckling load reduces rapidly for longer duration of application of loads. Figure 8 shows the deformed shape of laminated composite curved panel with R/a = 2, at point of loading and deformation scale factor = 3.

Fig. 7
figure 7

Effect of radius of curvature on dynamic buckling load

Full size image
Fig. 8
figure 8

Deformed shape of laminated composite curved panel with R/a = 2 and b/a = 1

Full size image

4 Conclusion

The conclusions of the study are summarised below.

  1. 1.

    The nonlinear dynamic buckling load for a laminated composite curved panel gradually reduces as the loading duration is increased.

  2. 2.

    When the loading duration is small, the nonlinear dynamic buckling load can be higher than static buckling load.

  3. 3.

    For very short duration of loading, the effect of aspect ratio is significant initially. This gradually reduces as the aspect ratio is increased. When the loading duration is increased, the variation in nonlinear dynamic buckling load is insignificant.

  4. 4.

    For a particular loading duration, the effect of radius of curvature on the variation in nonlinear dynamic buckling load is low. With the increase in loading duration, the effect of radius of curvature is minute.