An Efficient Sparse Coding-Based Data-Mining Scheme in Smart Grid

Abstract

With the availability of Smart Grid, disaggregation, i.e. decomposing a whole electricity signal into its component appliances has gotten more and more attentions. Now the solutions based on the sparse coding, i.e. the supervised learning algorithm that belongs to Non-Intrusive Load Monitoring (NILM) have developed a lot. But the accuracy and efficiency of these solutions are not very high, we propose a new efficient sparse coding-based data-mining (ESCD) scheme in this paper to achieve higher accuracy and efficiency. First, we propose a new clustering algorithm – Probability Based Double Clustering (PDBC) based on Fast Search and Find of Density Peaks Clustering (FSFDP) algorithm, which can cluster the device consumption features fast and efficiently. Second, we propose a feature matching optimization algorithm – Max-Min Pruning Matching (MMPM) algorithm which can make the feature matching process to be real-time. Third, real experiments on a publicly available energy data set REDD [1] demonstrate that our proposed scheme achieves a for energy disaggregation. The average disaggregation accuracy reaches 77% and the disaggregation time for every 20 data is about 10 s.

1 Introduction

Data mining is an efficient technique that shows the interesting patterns or knowledge from huge amount of data. These patterns play an important role in marketing, business, medical analysis, intrusion detection, and other applications where these patterns are of paramount importance for strategic decision making [21].

In Smart Grid, Energy disaggregation, the task of separating the whole energy signal of a residential, commercial, or industrial building into the energy signals of individual appliances, is a kind of important data mining method for energy-saving and by Energy disaggregation, we can disaggregate electricity consumptions to infer what device is used, how often this device is used. If this data is used by the supplier, amount of advertising fees may be saved and they can make a precise advertising for each family. They can even know which device needs to be fixed [24, 25].

Studies on energy disaggregation date back to about thirty years ago. The early approaches look for sharp edges (corresponding to device on/off events) in both the real and reactive power signals, and cluster devices according to these changes in consumption [2,3,4,5,6]. A number of different directions has been explored, [22, 23] computing harmonics of steady-state power to determine more complex device signatures, [24] analyzed the transient noise of a device circuit when the device changes state. But now for costs and convenience more and more researches focus on disaggregate electricity using low-frequency-resolution [7,8,9]. In this paper, we use a novel clustering algorithm based on sparse coding to disaggregate electricity in low frequency data set.

In this paper, we propose a new scheme–ESCD to make Energy disaggregation. The main contributions are as follows:

• 1. In the scheme we first proposes a new clustering algorithm–Probability Based Double Clustering (PBDC) based on Fast Search and Find of Density Peaks Clustering (FSFDP) algorithm in energy disaggregation, which can cluster the device consumption features fast and efficiently.

• 2. Our scheme proposes a feature matching optimization algorithm – Max-Min Pruning Matching (MMPM) algorithm, without any constraint condition, our algorithm can make the feature matching process to be real-time.

• 3. Experiments show that our scheme (ESCD) has a better Energy disaggregation accuracy and real-time performance than the sparse-coding based schemes before.

2 Related Work

The basic problem in this paper is energy disaggregation (the task of determining the component appliance contributions from an aggregated electricity signal) [1]. The user’s behavior of electricity consumption can be obtained by energy disaggregation, the solutions of which are varied. According to different types of basic data sets, the solutions can be divided into two categories. The first is the scheme based on the high frequency data [10,11,12], and the second is based on the low frequency data [7,8,9, 13,14,15,16,17,18]. The schemes based on the high frequency data can obtain more accurate analysis results. But the hardware for data sampling is very expensive. It requires one or more than one sensor per appliance to perform Appliance Load Monitoring (ALM). Namely Intrusive Load Monitoring (ILM) that is contrary to the issue studied in this paper. The scheme based on the low frequency data just requires only a single meter for per house or a building, the scheme is called Non-Intrusive Load Monitoring (NILM). The NILM schemes are divided into supervised [15,16,17] and unsupervised [7,8,9, 18] disaggregation algorithms. Most unsupervised disaggregation algorithms are developed based on the HMM. They can have good results in estimating the total electricity consumption per device, while the analysis for the time-sharing of each device is not good compared to the supervised ones [26]. Most supervised disaggregation algorithms are based on the sparse coding. For example, [16] uses a data set provided by Plugwise which contains ten broad categories of electrical devices from several houses. It models the entire signal of each device over a long period of time, such as a week, as a sparse linear combination of the atoms of an unknown dictionary [27]. However, the drawbacks of the algorithm are that it requires a large training dataset to capture all possible times that the same device may operate and the classification times cost too long. [15] uses the data set REDD, it proposes a concept: powerlets – a small period time, the electricity consumption of device measured by ‘powerlets’ and decoded by Dissimilarity-based Sparse subset Selection (DS3) [19] algorithm. The scheme can achieve the energy disaggregation accuracy of 72%, and the energy disaggregation speed is about 15 s. It is an efficient and accurate scheme, but it requires a lot of constraints, which causes the bad effect on the actual effect of this scheme. We propose a scheme in this paper, which improves the algorithm in [20]. We first use FSFDP algorithm and propose a feature matching optimization algorithm – max-min Pruning algorithm.

3 Preliminaries

We make a brief introduction to fast search and find of density peaks clustering and sparse coding.

3.1 Fast Search and Find of Density Peaks Clustering (FSFDP)

Clustering algorithm is an effective tool for data mining. Specifically, clustering analysis automatically groups things in the absence of category tag information. Each packet is self-identifying and differentiated from other groups [28].

Fast search and find of density peaks Clustering is a clustering algorithm, it is based on the idea that cluster centers are characterized by a higher density than their neighbors, and by a relatively large distance from points with higher densities. In FSFDP, the number of clusters arises intuitively, outliers are automatically spotted and excluded from the analysis, and clusters are recognized regardless of their shape and the dimensionality of the space in which they are embedded [21].

Assume that the data set $\mathrm{{S}} = \left\{ {{x_i}} \right\} _{i = 1}^N$, ${I_S} = \left\{ {1,2, \ldots ,N} \right\}$ to be clustered is the corresponding set of indices, and $d_{ij}$ represents the defined distance between the data points $x_i$ and $x_j$. For any data point $x_i$ in S, we can define two quantities of $\rho _i$ and $\delta _i$, which are the two characteristics of the clustering center mentioned above: local density and distance, respectively.

Local density $\rho _i$ is calculated by two ways: Cut-off kernel or Gaussian kernel.

Cut-off kernel and Gaussian kernel are calculated by Eqs. 1 and 2:

$$\begin{aligned} {{\rho _i} = \sum \limits _{j \in {I_s}\backslash \{ i\} } {\chi ({d_{ij}} - {d_\mathrm{{c}}})} } {\chi (x) = \left\{ \begin{array}{l} 1,x < 0;\\ 0,x \ge 0. \end{array} \right. } \end{aligned}$$

(1)

$$\begin{aligned} {{\rho _i} = \sum \limits _{j \in {I_s}\backslash \{ i\} } {{e^{ - {{(\frac{{{d_{ij}}}}{{{d_c}}})}^2}}}} } \end{aligned}$$

(2)

The parameter $d_c>0$ is the cutoff distance and must be specified in advance. $\rho _i$ represents the number of data points in the S where the distance is less than $d_c$ (regardless of the itself). In Gaussian kernel, the distance between the data point j and i($d_{ij}<d_c$) is greater, the value of $\rho _i$ is greater. The only difference is that the cut-off kernel is a discrete value and the Gaussian kernel is a continuous value, the probability of the latter is conflicting (i.e., the local density values of the same data points with the same distance) are smaller.

We calculate the distance ${\delta _i}$ as follows:

Let $\left\{ {{q_i}} \right\} _{i = 1}^N$ be a descending order of $\left\{ {{\rho _i}} \right\} _{i = 1}^N$, ${\rho _{{q_1}}} \ge {\rho _{{q_2}}} \ge \cdots \ge {\rho _{{q_N}}}$.

$$\begin{aligned} {{\delta _{{q_i}}} = \left\{ {\begin{array}{*{20}{l}} {\mathop {\min \limits _{q_j, \mathrm{{j}}} \{ {d_{{q_i}{q_j}}}\},i \ge 2;}}\\ {\mathop {\max }\limits _{j \ge 2} \{ {d_{{q_i}{q_j}}}\},i = 1.} \end{array}} \right. } \end{aligned}$$

(3)

$$\begin{aligned} {{\delta _i} = \left\{ \begin{array}{l} \mathop {\min }\limits _{j \in I_s^i} \{ {d_{ij}}\},I_s^i \ne \varPhi ;\\ \mathop {\max }\limits _{j \in {I_s}} \{ {d_{ij}}\},I_s^i = \varPhi . \end{array} \right. } \end{aligned}$$

(4)

The set $I_s^i = \{ k \in {I_s}:{\rho _k} > {\rho _i}\}$, when $x_i$ has the maximum local density, $\delta _i$ represents the distance between the data point and $x_i$ with the largest distance from $x_i$ in S, otherwise $\delta _i$ represents the shortest distance that in all data points with local density greater than $x_i$. We can choose some appropriate value of $\rho _i$ and $\delta _i$ as critical value to cluster.

3.2 Sparse Coding

Sparse coding is a class of unsupervised methods for learning sets of over-complete bases to represent data efficiently. The aim of sparse coding is to find a set of basis vectors ${\phi _\mathrm{{i}}}$ such that we can represent an input vector X as a linear combination of these basis vectors [21]:

$$\begin{aligned} {X = \sum \limits _{i = 1}^k {{a_i}} {\phi _\mathrm{{i}}}} \end{aligned}$$

(5)

We define sparsity as having few non-zero components or having few components not close to zero. The requirement that our coefficients ${a_i}$ be sparse means that given a input vector, we would like as few of our coefficients to be far from zero as possible. The choice of sparsity as a desired characteristic of our representation of the input data can be motivated by the observation that most sensory data such as natural images may be described as the superposition of a small number of atomic elements such as surfaces or edges. Other justifications such as comparisons to the properties of the primary visual cortex have also been advanced [22].

We define the sparse coding cost function on a set of m input vectors as [23]:

$$\begin{aligned} {\mathrm{\min \limits _{a_i^{(j)}}}\ \ \ {\phi _i}{\sum \limits _{j = 1}^m {\left\| {{X^{(j)}} - \sum \limits _{i = 1}^k {\mathrm{{a}}_i^{(j)}{\phi _i}} } \right\| } ^2} + \lambda \sum \limits _{i = 1}^k {S(\mathrm{{a}}_i^{(j)})} } \end{aligned}$$

(6)

where S(.) is a sparsity cost function which penalizes ${a_i}$ for being far from zero. We can interpret the first term of the sparse coding objective as a reconstruction term which tries to force the algorithm to provide a good representation of X and the second term as a sparsity penalty which forces our representation of X to be sparse. The constant ${\lambda }$ is a scaling constant to determine the relative importance of these two contributions [29].

Although the most direct measure of sparsity is the ‘L0’ norm $(S({a_i}) = 1(|{a_i}| > 0))$, it is non-differentiable and difficult to optimize in general. In practice, common choices for the sparsity cost S(.) are the ${L_1}$ penalty $S({a_i})=|{a_i}|_1$ and the log penalty $S({a_i}) = \log (1 + a_i^2)$.

In addition, it is also possible to make the sparsity penalty arbitrarily small by scaling down ${a_i}$ and scaling ${\phi _\mathrm{{i}}}$ up by some large constant. To prevent this from happening, we will constrain $\left\| {{\phi ^2}} \right\|$ to be less than some constant C. The full sparse coding cost function including our constraint on $\phi$ is

$$\begin{aligned} {\begin{array}{l} \mathrm{\min \limits _{a_i^{(j)}}}\ \ \ {\phi _i}\sum \limits _{j = 1}^m {{{\left\| {{X^{(j)}} - \sum \limits _{i = 1}^k {\mathrm{{a}}_i^{(j)}{\phi _i}} } \right\| }^2}} + \lambda \sum \limits _{i = 1}^k {S(\mathrm{{a}}_i^{(j)})} \\ \mathrm{{subject\ to\ }}{\left\| \phi \right\| ^\mathrm{{2}}} \le C,\forall i = 1, \ldots ,k \end{array}} \end{aligned}$$

(7)

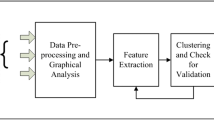
4 Efficient Sparse Coding-Based Data-Mining (ESCD) Scheme

In this section we propose a novel energy disaggregation scheme, ESCD Scheme. Based on sparse coding, this is an efficient and fast scheme for energy disaggregation. First, we carry out a detailed description of the problem. We assume that there are n electrical devices in a building, where $x_i(t)$ denotes the energy signal of device i at time t. y(t) denotes the aggregate energy signal, recorded by a smart meter, at time t. We can write

$$\begin{aligned} {y\left( t \right) = \mathop \sum \limits _{i = 1}^n {x_i}\left( t \right) } \end{aligned}$$

(8)

Given only the whole power consumption $y\left( t \right)$, the goal of energy disaggregation is to recover the power signal of each of the appliances, i.e., to estimate ${x_i}\left( t \right)$ for $\mathrm{{i}} \in \left\{ {1,2,3, \ldots ,\mathrm{{n}}} \right\}$. It is very difficult to solve the formula (8) because ${x_i}\left( t \right)$ represents the $i-th$ electricity consumption of the device at the time t, and the electrical device is operated by the person. We can not judge the human behaviour at time t that we can’t get ${x_i}\left( t \right)$.

In this paper, we model each electrical device with sparse coding. For every $i = 1,2,3,\ldots ,n$, n, we learn a feature matrix from training set whose frequency is q Hz, ${X_i} \in {R^{{m_i} \times {T_w}}}$, ${T_w}$ we call sliding window time represents a continuous period of time from training time ${T_{tr}}$ and ${T_w} \ll {T_{tr}}$. ${m_i}$ represents the number of features in the $i-th$ electrical device. If we have got enough features from the $i-th$ electrical device, we can use the approximation

$$\begin{aligned} {\begin{array}{ll} {T_w}\left( {{x_i}\left( t \right) } \right) &{} \approx {X_i}{a_i}\left( t \right) ,{T_w}\left( {{x_i}\left( t \right) } \right) \\ &{}= \left( {{x_i}\left( t \right) ,{x_i}\left( {t + \frac{1}{\mathrm{{q}}}} \right) ,{x_i}\left( {t + 2 \times \frac{1}{\mathrm{{q}}}} \right) , \ldots ,{x_i}\left( {t + {T_w}} \right) } \right) \end{array}} \end{aligned}$$

(9)

We call the vector ${T_w}\left( {{x_i}\left( t \right) } \right)$ sliding window, ${a_i}\left( t \right)$ is the activations of feature matrix ${X_i}$, ${a_i}\left( t \right)$ is sparse that contain mostly zero elements and only a 1 elements. We propose a matching algorithm to get the ${a_i}\left( t \right)$ so that we can calculate ${X_i}{a_i}\left( t \right)$ to get an approximate solution for each device. Our scheme based on sparse coding is consist of two stages, learning feature matrix and energy matching.

4.1 Learning Feature Matrix

We propose a Probability Based Double Clustering (PBDC) algorithm to learning each of the electrical devices feature matrix. As described above, the time length of training data is ${T_{tr}}$, frequency is q Hz, there are $\left( {{T_{tr}} - {T_w} + 1} \right) \times \mathrm{{q}}$ sliding windows, for each sliding window, we have ${T_w} \times \mathrm{{q}}$ elements. Assume that every sliding window is a data point ${\mathrm{{P}}_{i}} \in \left( {1,\left( {{T_{tr}} - {T_w} + 1} \right) \times \mathrm{{q}}} \right)$, after removing the repeated points we get k unique points set $P_{uniq}$ and a vector representing the repeat times of data points $\mathrm{{R}} = \left( {{r_1},{r_2},{r_3}, \ldots ,{r_k}} \right)$, we define the distance between two point ${d_{ij}} = \left\| {{P_i} - {P_j}} \right\| {}_2$, the distance matrix D is a $\mathrm{{k}} \times \mathrm{{k}}$ scale symmetric matrix with a diagonal of 0, $\mathrm{{D}} = \left\{ {{\mathrm{{d}}_{ij}},\mathrm{{i}},\mathrm{{j}} \in \left\{ {1,2,3, \ldots ,k} \right\} } \right\}$, PBDC algorithm is based on FSFDP, the FSFDP algorithm needs to manually specify the minimum value of $\rho$ and $\delta$ to determine the boundary of the cluster that to determine the number of clustering centres, this operation will lead to the instability of the number of clustering centres and can not get the scheme to be automated.

Fig. 1.

(a) and (b) are the electricity consumption of refrigerator and lighting.

In this paper, the algorithm is improved by setting a upper limit of the number m, when clustering we will compare the difference of m and the number of clusters, and make a automatically correct until the number of clusters is similar to m. In this improved algorithm, it is only necessary to specify the upper limit of the number m of clustering centres before clustering instead of manually specify the minimum value of $\rho$ and $\delta$ during clustering. Therefore, we can have an efficient clustering and the number of clustering centres can be stabilized at a certain controllable value. Every clustering centre is an electrical device feature, a controllable number of electrical device feature is necessary for reduce the algorithm complexity of energy matching.

After first clustering, we find some problem, the clustering result is not what we really want. According to the power consumption of electrical equipment and the relationship between time, as shown in Fig. 1.

It is clear that after the first clustering, the centre point represents the larger distance from the data points, and the result is just judged by the data value difference, this will lead a result that some data points with small value is buried in large. In fact, we need a more comprehensive clustering to make a second clustering for improving this result.

In the second clustering, we need to do cluster for every clusters calculated in the first clustering. And we set the number of cluster by the probability set C that includes the probability $C_i$ of each cluster. Considering the repeated points, the probability $C_i$ of each cluster can be calculated by formula 10 and 11.

$$\begin{aligned} {{\mathrm{{C}}_{i}} = \frac{{num\left( {Cluster_i} \right) }}{{\mathop \sum \nolimits _{i = 1}^k {r_i}}}} \end{aligned}$$

(10)

$$\begin{aligned} {num\left( {Cluster_i} \right) = \mathop \sum \nolimits {r_i},{r_i} \in \left\{ {Cluster_i} \right\} } \end{aligned}$$

(11)

Assume that we need about m features in each electrical device, we can set the upper limit $\mathrm{{m}} \times {\mathrm{{C}}_{i}}$ for each cluster and clustering again. The algorithm details describe in Algorithm 1.

4.2 Energy Matching

According to the first stage, we obtain the feature matrix of each device $X_i$, as seen in formula (9), in this stage, we need to calculate ${a_i}\left( t \right)$. Considering the constraint of ${a_i}\left( t \right)$ that ${a_i}\left( t \right)$ has only one element is 1 and other is 0.

In general, in order to get a globally optimal solution with n electrical devices, if the number of feature matrix in each electrical device $X_i$ is $m_i$, the algorithm complexity is $\mathrm{{O}}\left( \mathop {\prod \limits _{i = 1}^n {m_i}} \right)$. We can find that the complexity of the algorithm increases exponentially with each additional device, and the complexity of this algorithm is unacceptable. We need to do some algorithm optimization, consider that n is a constant determined by the number of equipment and $m_i$ is the number of electrical device feature, it will lead to a poor accuracy if we reduce the $m_i$. We propose a Max-Min Pruning Matching (MMPM) algorithm.

The purpose of the algorithm is to perform the pruning optimization of the matching algorithm under the condition of guaranteeing the global optimum. This optimization can be divided into two operations: minimum pruning and maximum pruning, set the maximum pruning parameters for $arg_{max}$, the pruning threshold for $\mu$. We first discuss the minimum pruning.

The goal of maximum pruning can make sure that we can get the global optimal solution and end the loop as soon as possible when we get the global optimal solution. To do this option, we should get the order j of the maximum element in ${T_w}\left( {y\left( t \right) } \right)$. And then sort in each feature matrix ${X_i},i \in \left\{ {1,2,3 \ldots ,n} \right\}$ by the j-th element in descending order, we set the maximum element of feature matrix $X_i$ in j-th column $max_i$. We calculate the maximum pruning parameters as below

$$\begin{aligned} {ar{g_{max}} = y\left( {t + \left( {j - 1} \right) q} \right) - \mathop \sum \limits _{i = n - i}^n ma{x_i}} \end{aligned}$$

(12)

When $ar{g_{max}} > \mu$, it means that the $arg_{max}$ in remaining loop will large than the pruning threshold, the remaining loop should be cutoff.

The goal of minimum pruning aids to cut the invalid loop when the sliding windows vector is to small. In each loop, we get a remainder energy ${T_w}\left( {r\left( t \right) } \right)$ which is the difference between total energy ${T_w}\left( {\mathrm{{y}}\left( t \right) } \right)$ and the upper loop, we make a minimum pruning judgement condition

$$\begin{aligned} {\mathrm{{min}}\left( {{T_w}\left( {r\left( t \right) } \right) } \right) + \mu < 0} \end{aligned}$$

(13)

If this judgement condition is set up, that proves it the remaining loop will make the $\mathrm{{min}}\left( {{T_w}\left( {r\left( t \right) } \right) } \right)$ more and more small, we should cut off the remaining invalid loop. The algorithm details describe in Algorithm 2.

Fig. 2.

(a) and (b) are the relationship of disaggregation accuracy and time with feature vector numbers.

5 Experiment Analysis

In this section, we evaluate our propose scheme on the real-world REDD data set [1], a publicly available data set for electricity disaggregation. The data set consists of power consumption signals from six different houses, where for each house, the whole electricity consumption as well as electricity consumptions of about twenty different devices are recorded. The signals from each house are collected over a period of two weeks with a low frequency sampling rate of 1/3 Hz. The House 5 data set is excluded because of its data contains very few fluctuation that we could not extract enough features to do energy disaggregation.

In the experiment, in every house we use a month of recorded electricity signals that include 5 important household appliances, one week for learning feature matrix and the rest for energy matching. We set the size of feature matrix as $20 \times m$ that means the size of a feature vector is set to 20 and the numbers of feature vector is set to m. The size of feature vector too small or to large may lead to a low performance because that a small size could cause excessive training and a large size could confusion the features. In order to make a real-time energy matching the numbers of feature vector m must be less than 100. With these settings, we can get five feature matrix for five household appliances, it takes about 10 s to perform energy matching on a temporal window. We compute the disaggregation accuracy, similar to [1]:

$$\begin{aligned} {ac{c_{\mathrm{{energy\ matching}}}} = 1 - \frac{{\sum \limits _{t \in \psi } {\sum \limits _{i = 1}^M {{{\left\| {{\mathrm{{T}}_w}\mathrm{{(}}{\mathrm{{x}}_i}\mathrm{{(t))}} - {{\mathrm{{\tilde{T}}}}_w}\mathrm{{(}}{\mathrm{{x}}_i}\mathrm{{(t))}}} \right\| }_1}} } }}{{2\sum \limits _{t \in \psi } {{{\left\| {{\mathrm{{T}}_w}\mathrm{{(}}{\mathrm{{x}}_i}\mathrm{{(t))}}} \right\| }_1}} }}} \end{aligned}$$

(14)

where $\psi = \{ 1,{T_w} + 1,2{T_w} + 1, \ldots \}$ and the 2 factor in the denominator comes from the that the absolute value results in double counting errors. We compare our method with the PED algorithm [15], FHMM algorithm (in its supervised setting) [1] and a Simple Mean prediction algorithm, which estimates the total consumption percentage of each device and predicts that the whole electricity signal breaks down according to this percentage at all time.

Fig. 3.

(a) and (b) the actual and estimated energy consumption obtained by ESCD scheme for refrigerator and lighting in the House 1

Figure 2 shows the disaggregation accuracy and time of our algorithm for different houses as a function of feature vector numbers m when size of a feature vector is set to 20. Table 1 shows the disaggregation results for all the six houses (exclude the House 5) in the REDD data set. Our algorithm performs better than PED, FHMM and the naive Simple Mean on the data set, achieving about 5.4% higher accuracy overall. Figure 3 shows the actual and estimated energy consumption obtained by our method for refrigerator and lighting in the House 1. Our scheme captures transients and different steady states in each device.

Table 1. Energy disaggregation accuracies (%)

6 Conclusion

In this paper, we propose a new algorithm for energy disaggregation which consists of the two steps of learning feature matrix of power consumption signatures and a energy matching for disaggregation. To learn feature matrix, based on FSFDP algorithm we propose the Probability Based Double Clustering (PBDC) algorithm to learning each of the electrical devices feature matrix, the PBDC algorithm can make a second clustering according to the first clustering points distribution probability and ensure that the clustering can extract sufficient feature vector and avoid excessive training. After we calculate feature matrix of each devices, we propose a Max-Min Pruning Matching (MMPM) energy matching algorithm for disaggregation. The MMPM algorithm can minimize computational complexity make the disaggregation be a real-time calculation. Our experiments are based on a real energy data set, we show that our scheme provides promising results for energy disaggregation.