Integral Super Twisting Sliding Mode Control (ISTSMC) Application in 1DOF Internal Mass Autonomous Underwater Glider (AUG)

Abstract

This paper presents the design and implementation of the integral super twisting sliding mode control for the tracking control of a linearized model of longitudinal plane autonomous underwater glider. The performance of the proposed controller is evaluated in terms of chattering reduction in control input for the nominal system as well as the system in the presence of external disturbance. The controller is designed for the gliding path from 45° to 30° downward and upward. The performance of the proposed controller is compared with the quasi sliding mode control (boundary layer), integral sliding control, and super twisting sliding mode control. The simulation results have shown that the proposed controller is able to eliminate the undesired chattering.in control inputs.

1 Introduction

Underwater offers a wide range of research opportunities. Autonomous underwater vehicles (AUVs) are amongst the popular of underwater vehicles used in underwater for data gathering. While autonomous underwater gliders (AUGs) are considered as a new class of AUVs where the idea was initiated by Henry Stommel in 1989 [1]. However the real operational AUGs are realized more than a decade later when Slocum AUG, Seaglider AUG and Spray AUG were successfully designed, developed, and tested in 2001. The ideal AUG slides the internal movable mass translational and/or rotational and the ballast is pumped back and forth for controlling its position and attitude.

The maneuverability of AUG in underwater is very much depending on the underwater environment. Many control techniques are reported being employed to control the motion of AUG in underwater. The classical control proportional-integral-derivative (PID) controller have been proposed in [2, 3] is based on the single-input-single-output system. The optimal control known as linear quadratic regulator (LQR) was proposed in [4,5,6]. The LQR offers very simple design that involves two tuning parameters Q and R to obtain the optimal performance in which minimizing the cost function (J) and become the solution for the Ricatti’s equation. In [4,5,6], the LQR was designed for the system without perturbation. The nonlinear control approach such as model predictive control (MPC) is proposed in [7, 8] and sliding mode control is proposed in [9]. The MPC is also known as Receding Horizon Control and Moving Horizon Optimal Control. In [7] the MPC is designed for controlling the attitude of the Slocum glider where the control architecture is divided into inner and outer loops. The inner loop is responsible for internal glider configuration and outer loop to control the attitude of the glider. Ian Abraham and Jingang Yi in [8] developed the MPC to control the horizontal plane of the glider. The MPC is integrated with the time suspension technique to enable online tuning capability. The sliding mode control (SMC) is employed by Hai Yang and Jie Ma as in [9] to control the pitch angle and the net buoyancy of the glider. The SMC is formulated for the nonlinear longitudinal plane of the glider. The intelligent method is proposed in [10, 11]. In [10] the homeostatic method is formulated to control the motion of the USM hybrid-driven underwater glider. The algorithm is based on emergent approach which combining the property of artificial neural network (ANN), artificial endocrine system (AES) and artificial immune system (AIS). The neural network (NN) is employed in [11] also to control the motion of the USM hybrid-driven underwater glider. The predictive control is designed based on neural network multilayer (three layer) perceptron with six input nodes, six hidden layer nodes and fourteen output nodes.

In this paper the integral super twisting sliding mode control (ISTSMC) is proposed for the linearized model of the AUG longitudinal plane. The model is linearized using Taylor’s series expansion method as proposed by J. Graver in 2005 [12]. The proposed controller is considered as a new approach in regards to linearized model of the AUG application and will be the contribution for this paper. The paper is organized as follows. The glider system is explained in Sect. 2. In Sect. 3, the controller design procedures are presented. The result and discussion are explained in Sect. 4 and finally the paper is summarized in Sect. 5.

2 Glider System

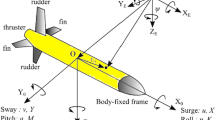
The glider model is discussed in this section. The model is restricted to longitudinal plane dynamics where the internal only move along the x-axis. The detail derivation is shown in [13].

The linearized model of a longitudinal plane is computed using Taylor’s series expansion method. The linearization is performed for the gliding equilibrium as computed by J. Graver in [12]. Consider the following general nonlinear equations.

$$ \begin{array}{*{20}c} {\dot{x}_{1} = f_{1} \left( {x_{1} , \ldots ,x_{n} ,u_{1} , \ldots ,u_{m} } \right)} \\ \vdots \\ {\dot{x}_{n} = f_{n} \left( {x_{1} , \ldots ,x_{n} ,u_{1} , \ldots ,u_{m} } \right)} \\ \end{array} $$

(1)

The approximation of nonlinear equations in (1) is performed by computing the gradient of the nonlinear equations with respect to the state vectors and input vectors respectively. The general linear system is defined in Eq. (2).

$$ \delta \dot{x} = A\delta x + B\delta u + Bh\left( {x,t} \right) $$

(2)

where

$\delta x = x - x_{d}$, $\delta u = u - u_{d}$ and $h\left( {x,t} \right)$ is the disturbance. $u_{d}$ is set to zero then Eq. (2) become

$$ \delta \dot{x} = A\delta x + Bu + Bh\left( {x,t} \right) $$

(3)

The system matrix A and input matrix B are obtained using Eq. (4).

$$ \begin{aligned} & A = \left. {\frac{\partial f}{\partial x}} \right|_{{x_{e,} u_{e} }} \in {\Re }^{n \times n} \\ & B = \left. {\frac{\partial f}{\partial u}} \right|_{{x_{e,} u_{e} }} \in {\Re }^{m \times n} \\ \end{aligned} $$

(4)

The matrices A and B for AUG longitudinal plane for downward and upward glides are given in Eq. (5) and (6) respectively.

$$ \begin{aligned} & A_{d} = \left[ {\begin{array}{*{20}c} 0 & {1.0000} & 0 & 0 & 0 & 0 & 0 \\ { - 7.1379} & {0.0079} & { - 6.5792} & 0 & { - 174.4810} & 0 & { - 0.1708} \\ { - 0.1709} & { - 0.0531} & { - 0.6366} & {1.1003} & {0.8959} & 0 & {0.2537} \\ {0.0439} & {0.1638} & { - 0.3524} & { - 3.4850} & { - 0.0335} & 0 & {0.3251} \\ 0 & 0 & 0 & 0 & 0 & {1.0000} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right] \\ & B_{d} = \left[ {\begin{array}{*{20}c} 0 & 0 \\ { - 0.6782} & 0 \\ { - 0.1249} & 0 \\ { - 0.0002} & 0 \\ 0 & 0 \\ {1.0000} & 0 \\ 0 & {1.0000} \\ \end{array} } \right] \\ \end{aligned} $$

(5)

$$ \begin{aligned} & A_{u} = \left[ {\begin{array}{*{20}c} 0 & {1.0000} & 0 & 0 & 0 & 0 & 0 \\ { - 9.9372} & {0.0797} & {7.1377} & 0 & { - 162.7320} & 0 & { - 0.0617} \\ {0.2732} & {0.0538} & { - 0.7413} & { - 0.4095} & {0.8761} & 0 & { - 0.2556} \\ {0.0810} & {0.1602} & {0.3386} & { - 3.3597} & {0.9299} & 0 & {0.3376} \\ 0 & 0 & 0 & 0 & 0 & {1.0000} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right] \\ & B_{u} = \left[ {\begin{array}{*{20}c} 0 & 0 \\ { - 0.6548} & 0 \\ { - 0.1311} & 0 \\ {0.0020} & 0 \\ 0 & 0 \\ {1.0000} & 0 \\ 0 & {1.0000} \\ \end{array} } \right] \\ \end{aligned} $$

(6)

The AUG has seven states ($\theta ,\omega_{2} ,v_{1} ,v_{3} ,r_{p1} ,\dot{r}_{p1} ,m_{b}$) and two inputs ($u_{1} ,u_{2}$) as defined in Table 1. The eigenvalues of the open loop system for downward and upward glides are depicted in Table 2. The controllability and observability are full rank. The open loop system is stable since all the eigenvalues are laid on left-hand plane (LHP) except three zero eigenvalues indicate marginally stable.

Table 1 Parameter definition

Table 2 The eigenvalues, controllability and observability of AUG open loop system

3 Controller Design

The controllers are designed for the gliding path from 45° to 30° downward and upward. A glide path is specified by a desired gliding angle, $\varsigma_{d}$ and desired speed V _d .

$$ \varsigma_{d} = \theta - \alpha $$

(7)

where θ = pitching angle, α = angle of attack.

$$ V_{d} = \sqrt {v_{1}^{2} + v_{3}^{2} } $$

(8)

The conventional SMC is suffered from chattering phenomena due to high frequency oscillations induced by signum function where in practical, actuators unable to cope with high frequency oscillations. Therefore in this section all the controllers are designed to reduce the chattering and improve the system performance.

Consider the linear time invariant in Eq. (9)

$$ \delta \dot{x} = A\delta x + Bu + Bh\left( {x,t} \right) $$

(9)

where $x\, \in \,R^{n}$, and $u\, \in \,R^{m}$, are the state vectors, and input vectors which satisfies the following assumptions

• 1. The pair $\left( {A,B} \right)$ is controllable.

• 2. $h\left( {x,t} \right)$ is assumed known and in the range of input distribution $B$. $h\left( {x,t} \right)$ is a bounded matched perturbation that is a bounded with a known upper bound as defined in Eq. (10)

  $$ \left| {h\left( {x,t} \right)} \right| \le d $$

  (10)

Section 3.1 explains the controller design for the boundary layer sliding mode control which is also called quasi sliding mode control (QSMC) control design. Section 3.2 and Sect. 3.3 explain the design methodology for integral sliding mode control (ISMC) and super twisting sliding mode control (STSMC) respectively. Finally the proposed controller, integral super twisting (ISTSMC) is explained in Sect. 3.4.

The block diagram of the proposed controller is shown in Fig. 1. Two basic steps are involved in designing SMC based controllers. Firstly, the stable sliding manifold is designed so that the dynamic of the system is confined to the sliding manifold in which output responses converged to the desired values. Secondly control law is designed such that the system trajectory moves towards the sliding manifold, reach the sliding manifold and remain there.

Fig. 1

The block diagram of the integral super twisting sliding mode control (ISTSMC)

3.1 Quasi Sliding Mode Control (QSMC)

The quasi sliding mode control (QSMC) is another name for boundary layer approach. In this method a boundary layer is used to approximate the discontinuous function, signum. This approach is one of the approaches that can be used to reduce chattering phenomena induced by the discontinuous function.

The QSMC sliding manifold and control law are defined in Eqs. (11) and (12) respectively

$$ \sigma_{QSMC} = S\delta x\left( t \right) $$

(11)

$$ u_{QSMC} = u_{eq} + u_{dis} $$

(12)

where $S\, \in \,R^{mxn}$, $u_{eq}$ and $u_{dis}$ are the sliding gain, equivalent control and discontinuous control respectively. The $S$ is chosen such that $SB\, \in \,R^{mxn}$ is non-singular. From the underwater glider state-space system m = 2 and n = 8, therefore the sliding gain has 2 × 8 matrix structure.

The Lyapunov function and its derivative are defined in Eqs. (13) and (14).

$$ V\left( {\sigma_{QSMC} } \right) = \frac{1}{2}\sigma_{QSMC}^{2} $$

(13)

$$ \dot{V}\left( {\sigma_{QSMC} } \right) = \sigma_{QSMC} \dot{\sigma }_{QSMC} = \sigma_{QSMC} (S\left( {A\delta \left( x \right) + Bu + Bh\left( {x,t} \right)} \right) $$

(14)

The equivalent control is defined as $\dot{\sigma }_{QSMC} = 0$ as written in Eq. (15)

$$ u_{eq} = - (SB)^{ - 1} \left( {SA\delta \left( x \right) + SBh\left( {x,t} \right)} \right) $$

(15)

The reachability condition is chosen as in Eq. (16)

$$ u_{dis} = - M\frac{\sigma }{\left| \sigma \right| + \varepsilon } $$

(16)

where $M$ and $\varepsilon$ are the design parameter and boundary layer thickness and both are positive constants.

3.2 Integral Sliding Mode Control (ISMC)

The integral sliding mode control (ISMC) is known as a sliding mode control without reaching phase. The method was proposed by V. Utkin and J. Shi in 1996 [14]. The sliding and control law of the ISMC are defined in Eqs. (17) and (18).

$$ \sigma_{ISMC} \left( t \right) = S\delta x\left( t \right) + z\left( t \right) $$

(17)

$$ u_{ISMC} = u_{0} + u_{1} $$

(18)

where $u_{0}$ is the control law for system without perturbations and $u_{1}$ is the nonlinear control law for rejecting the perturbations. $S \in R^{m \times n}$ is the sliding gain and $z\left( t \right)$ is the integral term.

$u_{0}$ is designed using linear feedback control, linear quadratic regulator (LQR) and is defined as in Eq. (19).

$$ u_{0} = - F\delta x\left( t \right) $$

(19)

The Lyapunov function and its derivative are defined in Eqs. (20) and (21).

$$ V\left( {\sigma_{ISMC} } \right) = \frac{1}{2}\sigma_{ISMC}^{2} $$

(20)

$$ \dot{V}\left( {\sigma_{ISMC} } \right) = \sigma_{ISMC} \dot{\sigma }_{ISMC} = \sigma_{ISMC} (S\left( {A\delta \left( x \right) + B\left( {u_{0} + u_{1} } \right) + Bh\left( {x,t} \right)} \right) + \dot{z}\left( t \right) $$

(21)

and $\dot{z}\left( t \right)$ is chosen as in Eq. (22)

$$ \dot{z}\left( t \right) = - S\left( {A\delta x\left( t \right) + Bu_{0} } \right), z\left( 0 \right) = - S\delta x\left( 0 \right) $$

(22)

Substitute Eq. (22) into Eq. (21), then $u_{1}$ which consists of equivalent control and discontinuous control is defined as in Eq. (23).

$$ u_{1} = - \left( {SB} \right)^{ - 1} \left( {SBh\left( {x,t} \right)} \right) - Msign\left( {\sigma_{ISMC} } \right) $$

(23)

Finally, the overall control law of ISMC is written in Eq. (24)

$$ u_{ISMC} = - F\delta x\left( t \right) - \left( {SB} \right)^{ - 1} \left( {SBh\left( {x,t} \right)} \right) - Msign\left( {\sigma_{ISMC} } \right) $$

(24)

3.3 Super Twisting Sliding Mode Control (STSMC)

The super twisting sliding control (STSMC) was proposed by A. Levant in 1993 [15]. The sliding manifold and control law of STSMC are defined in Eqs. (25) and (26).

$$ \sigma_{STW} = S\delta x\left( t \right) $$

(25)

$$ u_{STW} = u_{1} + u_{2} $$

(26)

where $S \in R^{mxn}$, $u_{1}$ and $u_{2}$ are the sliding gain, continuous control and discontinuous time derivative control, respectively.

The Lyapunov function is defined in Eqs. (27).

$$ V\left( {\sigma_{STW} } \right) = \frac{1}{2}\sigma_{STW}^{2} $$

(27)

The STSMC control law is written in Eq. (28)

$$ u_{STW} = - h\left( {x,t} \right) - \left( {\beta_{1} \left| {\sigma_{STW} } \right|^{{\frac{1}{2}}} sign\left( {\sigma_{STW} } \right) + \beta_{2} \mathop \smallint \limits_{0}^{t} sign\left( {\sigma_{STW} } \right)d\tau } \right) $$

(28)

3.4 Integral Super Twisting Sliding Mode Control (ISTSMC)

The integral super twisting sliding mode control (ISTSMC) is an integration of the integral SMC and super twisting SMC. The sliding manifold and control law are defined based on ISMC as written in Eqs. (29) and (30)

$$ \sigma_{ISTW} \left( t \right) = S\delta x\left( t \right) + z\left( t \right) $$

(29)

$$ u_{ISTW} = u_{0} + u_{1} $$

(30)

where $u_{0}$ is the control law for system without perturbations and $u_{1}$ is the nonlinear control law for rejecting the perturbations. $S \in R^{mxn}$ is the sliding gain and $z\left( t \right)$ is the integral term.

$u_{0}$ was designed using linear feedback control, linear quadratic regulator (LQR) and is defined as in Eq. (31).

$$ u_{0} = - F\delta x\left( t \right) $$

(31)

The Lyapunov function and its derivative are defined in Eqs. (32) and (33).

$$ V\left( {\sigma_{ISTW} } \right) = \frac{1}{2}\sigma_{ISTW}^{2} $$

(32)

$$ \begin{aligned} \dot{V}\left( {\sigma_{ISTW} } \right) & = \sigma_{ISTW} \dot{\sigma }_{ISTW} = \sigma_{ISTW} (S\left( {A\delta \left( x \right) + Bu_{ISTW} + Bh\left( {x,t} \right)} \right) + \dot{z}\left( t \right) \\ & = \sigma_{ISTW} (S\left( {A\delta \left( x \right) + B\left( {u_{0} + u_{1} } \right) + Bh\left( {x,t} \right)} \right) + \dot{z}\left( t \right) \\ \end{aligned} $$

(33)

and $\dot{z}\left( t \right)$ is chosen as in Eq. (34)

$$ \dot{z}\left( t \right) = - S\left( {A\delta x\left( t \right) + Bu_{0} } \right), z\left( 0 \right) = - S\delta x\left( 0 \right) $$

(34)

Substitute Eq. (34) into Eq. (33), then time derivative of sliding manifold is reduced to Eq. (35)

$$ \dot{\sigma }_{ISTW} \left( t \right) = S\left( {Bu_{1} + Bh\left( {x,t} \right)} \right) $$

(35)

$u_{1}$ was defined based on super twisting algorithm is given in Eq. (36)

$$ u_{1} = - \left( {SB} \right)^{ - 1} \left( {Bh\left( {x,t} \right)} \right) + u_{dis} $$

(36)

where

$$ u_{dis} = u_{dis1} + u_{dis2} = - \beta_{1} \left| {\sigma_{ISTW} } \right|^{{\frac{1}{2}}} sign\left( {\sigma_{ISTW} } \right) - \beta_{2} \mathop \smallint \limits_{0}^{t} sign\left( {\sigma_{ISTW} } \right)d\tau $$

(37)

and

$$ u_{dis1} = \left\{ {\begin{array}{*{20}l} { - \beta_{1} \left| {\sigma_{0} } \right|^{1/2} sign\left( {\sigma_{ISTW} } \right)} \hfill & {\sigma_{ISTW} > \sigma_{0} } \hfill \\ { - \beta_{1} \left| {\sigma_{ISTW} } \right|^{1/2} sign\left( {\sigma_{ISTW} } \right) } \hfill & { \left| {\sigma_{ISTW} } \right| \le \sigma_{0} } \hfill \\ \end{array} } \right. $$

(38)

$$ \dot{u}_{dis2} = \left\{ {\begin{array}{*{20}l} { - u_{dis2} } \hfill & {\left| {u_{dis2} } \right| > 1} \hfill \\ { - \beta_{2} sign\left( {\sigma_{ISTW} } \right)} \hfill & {\left| {u_{dis2} } \right| \le 1} \hfill \\ \end{array} } \right. $$

(39)

Finally the control law for ISTSMC is written in Eq. (40).

$$ u_{ISTW} = - F\delta x\left( t \right) - \left( {SB} \right)^{ - 1} \left( {SBh\left( {x,t} \right)} \right) - \left( {\beta_{1} \left| \sigma \right|^{{\frac{1}{2}}} sign\left( \sigma \right) + \beta_{2} \mathop \smallint \limits_{0}^{t} sign\left( \sigma \right)d\tau } \right) $$

(40)

The closed loop error dynamic is computed by substituting back Eq. (36) into Eq. (35) gives the time derivative of Lyapunov function

$$ \dot{V}\left( {\sigma_{ISTW} } \right) = \sigma_{ISTW} \dot{\sigma }_{ISTW} = \sigma_{ISTW} ( - \beta_{1} \left| \sigma \right|^{{\frac{1}{2}}} sign\left( \sigma \right) - \beta_{2} \mathop \smallint \limits_{0}^{t} sign\left( \sigma \right)d\tau ) $$

(41)

To ensure the sufficient conditions for finite time convergence, the conditions in Eq. (42a, 42b) must be satisfied [16].

$$ \beta_{1}^{2} \ge \frac{{4C_{0} K_{M} \left( {\beta_{2} + C_{0} } \right)}}{{K_{m}^{2} K_{m} \left( {\beta_{2} - C_{0} } \right)}} $$

(42a)

$$ \beta_{2} > \frac{{C_{0} }}{{K_{m} }} $$

(42b)

4 Result and Discussion

This section presents the simulation results and discussions. The simulation is done using the parameters adopted from Graver (2005) [12]. The controllers are simulated for the gliding from 45° to 30° downward and upward using MATLAB/SIMULINK software. The simulations are performed for the nominal system and also for the system with induced external disturbance. The desired values of the observed parameters are shown in Table 3.

Table 3 Desired parameters’ values

The sliding gain, S is chosen to be the same for all controllers. The same sliding gain and linear feedback gain are used for the nominal system and system with external disturbance. The linear feedback gain, F and sliding gain, S for the downward and upward glides are written in Eqs. (43–46). No tunings are performed for the sliding gain and feedback gain. The tunings are performed for other controllers’ parameters only. All the controllers’ parameters for nominal system and system with external disturbance are depicted in Table 4 and Table 5, respectively.

Table 4 Controllers’ parameters (without disturbance)

Table 5 Controllers’ parameters (with disturbance)

$$ S_{d} = \left[ {\begin{array}{*{20}c} { - 197.223} & { - 107.5742} \\ { - 0.6370} & {0.0269} \\ \end{array} \begin{array}{*{20}c} {24.8201} & {0.5956} & {647.5100} \\ {56.3215} & {15.0971} & {33.0080} \\ \end{array} \begin{array}{*{20}c} { 8.1147} & {0.7552} \\ {7.8103} & {6.5436} \\ \end{array} } \right] $$

(43)

$$ S_{u} = \left[ {\begin{array}{*{20}c} { - 75.0704} & { - 73.9775} \\ { - 0.3635} & { - 0.0023} \\ \end{array} \begin{array}{*{20}c} { - 18.0774} & {0.1523} & {409.6529} \\ { - 13.1394} & {1.9503} & {7.1941} \\ \end{array} \begin{array}{*{20}c} { 5.9687} & {0.2550} \\ { - 1.4724} & {4.2390} \\ \end{array} } \right] $$

(44)

$$ F_{d} = \left[ {\begin{array}{*{20}c} { - 107.3832} & { - 74.4613} \\ {4.9429} & { - 1.1047} \\ \end{array} \begin{array}{*{20}c} {29.8753} & {312.7714} & {827.4601} \\ {58.5956} & {51.8619} & {122.73000} \\ \end{array} \begin{array}{*{20}c} { 15.8377} & {3.5445} \\ {10.2141} & {7.4767} \\ \end{array} } \right] $$

(45)

$$ F_{u} = \left[ {\begin{array}{*{20}c} { - 44.0298} & { - 33.8326} \\ {4.3815} & {2.6488} \\ \end{array} \begin{array}{*{20}c} { - 25.1949} & {225.0394} & {623.4317} \\ { - 21.5701} & {18.9855} & {48.1683} \\ \end{array} \begin{array}{*{20}c} { 16.4489} & {2.3837} \\ {1.3245} & {5.4174} \\ \end{array} } \right] $$

(46)

The simulation results for the nominal system and system with induced external disturbance are shown in Figs. 2, 3, 4, 5, 6, 7, 8 and 9 and Figs. 10, 11, 12, 13, 14, 15, 16 and 17 respectively. Figures 2, 3, 4 and 5 show that all the designed controllers are able to converge to the vicinity of the desired values with proposed controller shows the smallest steady-state error for all the observed outputs. The STSMC provides the highest steady error for the glide and pitch angles, however smaller errors show in ballast mass and net buoyancy. The ISMC provides second highest accuracy in glide and pitching angles, however the worst performance is shown in ballast mass and net buoyancy for the upward glide. The QSMC produce slightly better performance than the STSMC in glide and pitch angles and the worst performance shown in ballast mass and net buoyance for the downward glide. However, the proposed controller provides slower response (i.e. higher convergence time), in some cases.

Fig. 2

DOWNWARD—Glide angle ($\xi$) and pitch angle (θ)—Without disturbance

Fig. 3

UPWARD—Glide angle ($\varvec{\xi}$) and pitch angle (θ)—Without disturbance

Fig. 4

DOWNWARD—Ballast mass, m _b and net buoyancy, m _em —Without disturbance

Fig. 5

UPWARD—Ballast mass, m _b and net buoyancy, m _em —Without disturbance

Fig. 6

DOWNWARD—Control inputs u₁ and u₂—Without disturbance

Fig. 7

UPWARD—Control inputs u₁ and u₂—Without disturbance

Fig. 8

DOWNWARD—Sliding surfaces s₁ and s₂—Without disturbance

Fig. 9

UPWARD—Sliding surfaces s₁ and s₂—Without disturbance

Fig. 10

DOWNWARD—Glide angle ($\xi$) and pitch angle (θ)—With disturbance

Fig. 11

UPWARD—Glide angle ($\xi$) and pitch angle (θ)—With disturbance

Fig. 12

DOWNWARD—Ballast mass, m _b and net buoyancy, m _em —With disturbance

Fig. 13

UPWARD—Ballast mass, m _b and net buoyancy, m _em —With disturbance

Fig. 14

DOWNWARD—Control inputs u₁ and u₂—With disturbance

Fig. 15

UPWARD—Control inputs u₁ and u₂—With disturbance

Fig. 16

DOWNWARD—Sliding surfaces s₁ and s₂—With disturbance

Fig. 17

UPWARD—Sliding surfaces s₁ and s₂—With disturbance

From Figs. 6 and 7, all the controllers are able to stabilize in the vicinity of origin. The highest control effort in u ₂ for both glides is seen in ISMC, the STSMC shows the highest control effort in u ₁ for downward glide and the QSMC provides the highest control effort in u ₁ for upward glide, whereas the proposed controller demonstrates the lowest control effort in both input channels for both downward and upward glides with no undesired chattering. The sliding surface responses of all controllers in Figs. 8 and 9 are also stabilized in the vicinity of origin with the proposed controller provides no undesired chattering in its sliding surface responses.

The step input disturbance with magnitude of 1 is induced to both control input channels begins from t = 25 s. From Figs. 10, 11, 12 and 13, all the controllers are able to reject the induced disturbance with errors. The QSMC and STSMC show all the observed outputs are deviated from the desired values whereas the ISMC and the proposed controller are able to stabilize within the desired values with proposed controller gives the smallest steady-state error. The control effort of both channels for QSMC, ISMC and STSMC are not stabilized in the vicinity of origin as shown in Figs. 14 and 15 and the undesired chattering is also clearly can be observed. The proposed controller is able to stabilize to origin with no undesired chattering. The sliding surface responses in Figs. 16 and 17 have shown that the QSMC, ISMC and STSMC unable to stabilize within the origin with QSMC shows the highest deviation from origin for s ₁ and ISMC for s ₂ . Therefore, it can be concluded that the QSMC, ISMC and STSMC have lost their sliding mode. The sliding surfaces of the proposed controller are able to converge to zero and remain there and no undesired chattering is observed. The comparative analysis of all controllers is summarized Table 6.

Table 6 Comparative analysis of the controller

5 Conclusion

In this paper the integral super twisting (ISTSMC) is proposed for robust tracking for a linearized model of longitudinal plane of AUG. The performance of the proposed controller is compared with three other SMC controllers. Since the performance of the proposed controller is evaluated in terms of chattering reduction, therefore only controllers in SMC family are chosen for this work. The simulation results have shown that the proposed controller demonstrates the smallest steady-error and lowest control effort. The undesired chattering is also eliminated. The inconsistency performance is shown in QSMC, ISMC and STSMC may due to manual tuning and also the performance of the controllers only depend on the controllers’ gains. Therefore, in the future, the optimization method can be used to optimize the controllers’ gains, linear feedback gain and sliding gain and thus improve the performance of the controllers.