Keywords

1 Introduction

One of the most important characteristics for image analysis is its texture. Background subtraction (BS) Wu et al. [1] is one of the main steps in computer vision applications. Many challenging situations were faced by BS such as illumination changes, dynamic environments, inclement weather, camera jitter, noise, and shadows. For effective analysis, a descriptor histogram should be made that allows efficient matching of images. A good descriptor should have the following features: (i) tolerance to illumination changes, (ii) invariance to scale and rotation, (iii) robust to noise, and (iv) ability to capture nuances between images. Numerous local texture descriptors recently have attracted considerable attention, especially the local binary pattern (LBP) because it is simple to implement. However, the LBP operator produces a long feature set since it only adopts the first-order gradient information between the center pixel and its neighbors.

In this paper, we propose to modify G. Xue et al. [2], by combining it with the technique suggested by C. T. Ferraz et al. [3] so that the resulting method can capture nuances between images while preserving the advantages of G. Xue et al. [2]. In the same way, we also propose to modify C. Silva et al. [4] with the help of C. T. Ferraz et al. [3] technique.

The rest of the paper is organized as follows. Section 2 gives a brief literature review of the presently followed local description methods. Section 3 gives the basic idea and definitions of a few existing descriptors. Our proposed methods would be present in Sect. 4. We have considered a few existing local descriptors and compared their performances with our proposed methods in Sect. 5. Finally, we conclude our paper in Sect. 6.

2 Related Work

Various methods for texture classification are proposed in the literature. Firstly, in T. Ojala et al. [5] LBP was introduced as an approach for texture classification. After witnessing the success of LBP in texture classification, LBP finds its way into various classification problems such as facial recognition as proposed in T. Ahonen et al. [6]. The original LBP was rotation variant which sometimes can be seen as a disadvantage. To tackle this issue, in T. Ojala et al. [7] extended version of LBP was introduced which was rotation invariant. Later it was found out that LBP was sensitive to global intensity variations and also to local intensity along edge components. To handle these shortcomings in Bongjin Jun and Daijin Kim [8] a new method was introduced called local gradient pattern (LGP). LGP was shown to have higher discriminant power than LBP in the case of facial recognition. To improve recognition rate using LBP, in T. Ahonen et al. [6] an efficient method of facial representation was used. This new method of facial representation divides the image into small regions, and then on each region, LBP is applied and eventually the descriptor of each region is combined to form feature vector of the image. In M. Heikkilä et al. [9] a new method was introduced which combines the strengths of both LBP and SIFT operator called Center-Symmetric Local Binary Pattern (CS-LBP). It has many advantages such as low-size feature vector, tolerance to illumination changes, and robustness on flat image areas. Later, in C. Silva et al. [4] a new method called eXtended Center-Symmetric Local Binary Pattern (XCS-LBP) was introduced which combines both the strengths of CS-LBP and CS-LDP operator. Also in C. T. Ferraz et al. [3] a method called Center-Symmetric Local Mapped Pattern (CS-LMP) is presented which outperforms CS-LBP. Now to make this classification computationally efficient in Y. Zheng et al. [10] two approaches were proposed, i.e., dense Center-Symmetric Local Binary Patterns (CS-LBP) and pyramid Center-Symmetric Local Binary/Ternary Patterns (CS-LBP/LTP). These methods are computationally efficient than LBP and CS-LBP. Next, in A. Abdesselam [11] two LBP histograms were constructed, one for edge pixels and one for non-edge pixels. The final feature vector is the weighted combination of the two histograms.

3 Local Descriptors

In this section, we define the CS-LBP, CS-LDP, CS-LMP, and XCS-LBP and give brief explanation about them.

3.1 Center-Symmetric LBP Operator

The CS-LBP operator is a simple extension to the LBP operator which reduces the number of bins in the histogram drastically. For example, if \(P = 8\) and \(R = 1\) in LBP we get 256 bins. Whereas in CS-LBP only 16 bins would be needed. As mentioned in M. Heikkilä et al. [9], the CS-LBP operator produces features which are tolerant to illumination changes and robust in flat image areas and are straightforward to compute. T is a threshold value which is user defined. In our experiments, we always took it as 0. Equation 1 gives the mathematical model of CS-LBP.

$$\begin{aligned} CS-LBP_{(P,R,T)} (x,y) = \sum _{i=0}^{\frac{P}{2}-1} {s(n_i - n_{i + \frac{P}{2}})2^{i}} \end{aligned}$$
(1)

where

$$\begin{aligned} s(x) ={\left\{ \begin{array}{ll} \text {1} &{}\quad \text {if}\, x > T \\ \text {0} &{}\quad \text {otherwise} \end{array}\right. } \end{aligned}$$
(2)

3.2 Center-Symmetric LDP Operator

The CS-LDP operator was introduced by G. Xue et al. [2], and it claims that CS-LBP extracts only the first derivative and cannot extract multilevel derivative features. Hence, CS-LDP was made so that the problem could be alleviated and therefore captures more detailed texture information. This issue is because in CS-LBP the value of the center pixel was not considered whereas in CS-LDP it was considered. The following equation gives us the mathematical model of CS-LDP. Equation 3 gives the mathematical model of CS-LDP.

$$\begin{aligned} CS-LDP_{(P,R)} (x,y) = \sum _{i=0}^{\frac{P}{2}-1} {t((n_i - n_c).(n_c - n_{i + \frac{P}{2}}))2^{i}} \end{aligned}$$
(3)

where

$$\begin{aligned} t(x_1 . x_2) ={\left\{ \begin{array}{ll} \text {0} &{}\quad \text {if}\, x_1 . x_2 > 0 \\ \text {1} &{}\quad \text {otherwise} \\ \end{array}\right. } \end{aligned}$$
(4)

3.3 Center-Symmetric LMP Operator

Another issue of CS-LBP as pointed out by C. T. Ferraz et al. [3] is the following: The symmetric difference was thresholded by 1 or 0 and hence cannot capture the minute differences between images. This problem was mitigated by introducing a sigmoid function instead of a Heaviside step function. In our experiments, the value of \(\beta \) was always considered to be 1 for simplicity. It represents the slope of the sigmoid function. The value b is one less than the number of histogram bins. Equation 5 gives the mathematical model of CS-LMP.

$$\begin{aligned} CS-LMP_{(P,R,f)} (x,y) = round ( \frac{\sum _{i=0}^{\frac{P}{2}-1} {f(n_i - n_{i + \frac{P}{2}})2^{i}}}{\sum _{i=0}^{\frac{P}{2}-1} {2^{i}}})b \end{aligned}$$
(5)

where

$$\begin{aligned} f(x) =\frac{1}{1+e^{\frac{-x}{\beta }}} \end{aligned}$$
(6)

3.4 Extended Center-Symmetric LBP Operator

This operator produces a shorter histogram compared with LBP, and the length of the histogram is equal to that of CS-LBP. However, since the CS-LBP method does not make use of the center pixel C. Silva et al. [4], this approach was modified so that the center pixel value is considered and therefore extracting more information than CS-LBP. Equation 7 gives the mathematical model of XCS-LBP.

$$\begin{aligned} XCS-LBP_{(P,R)} (x,y) = \sum _{i=0}^{\frac{P}{2}-1} {s(g_1(i,c)+g_2(i,c))}2^i \end{aligned}$$
(7)

where

$$\begin{aligned} s(x_1 + x_2) ={\left\{ \begin{array}{ll} \text {1} &{}\quad \text {if}\, x_1 + x_2 \ge 0 \\ \text {0} &{}\quad \text {otherwise} \\ \end{array}\right. } \end{aligned}$$
(8)
$$\begin{aligned} g_1(i,c) = n_i - n_{i + \frac{P}{2}} + n_c, g_2(i,c) = (n_i - n_c)(n_{i + \frac{P}{2}} - n_c) \end{aligned}$$
(9)

The advantages of both CS-LMP, CS-LDP, and XCS-LBP motivated us to make methods which use the features of CS-LMP and CS-LDP, CS-LMP, and XCS-LBP, respectively. For example, the CS-LMP method does not use the center pixel value, and it does not give more detailed texture information. But we know that CS-LDP uses the center pixel value for the histogram calculation which gives more texture information. Therefore, using the features of CS-LMP and CS-LDP, we have discovered a new method which gives more texture information and captures nuances between images.

4 Proposed Local Descriptor Methods

In this section, we propose methods which use the advantages of multiple methods and finally prove it experimentally that it is indeed the case. Firstly, we offer Center-Symmetric Local Derivative Mapped Patterns (CS-LDMP), and next, we recommend eXtended Center-Symmetric Local Mapped Patterns (XCS-LMP).

4.1 Center-Symmetric Local Derivative Mapped Patterns (CS-LDMP)

Here, we propose to modify the threshold function of the CS-LDP operator to an amended version of the sigmoid function. The reason behind this is, as, in CS-LBP, CS-LMP did not consider center pixel values and hence useful texture information was not captured. Moreover, CS-LDP was not able to capture nuances between images. Hence, the proposed CS-LDMP overcame the difficulty and hence performed better than both CS-LDP and CS-LMP. The above results were tested on the CIFAR10 dataset as proposed in A. Krizhevsky and G. Hinton [12].

It is interesting to observe that the original definition of sigmoid function was not used but a modified version was used. In Eq. 3 we can see that the threshold function is a bit different from others like CS-LBP or XCS-LBP. We have changed the sigmoid function so that it looks like a continuous representation of the CS-LDP threshold function. The value b is one less than the number of histogram bins. Equation 10 gives the mathematical model of CS-LDMP.

$$\begin{aligned} CS-LDMP_{(P,R,f)} (x,y) = round(\frac{\sum _{i=0}^{\frac{P}{2}-1} {f((n_i - n_c).(n_c - n_{i + \frac{P}{2}}))2^{i}}}{\sum _{i=0}^{\frac{P}{2} - 1} {2^i}})b \end{aligned}$$
(10)

where

$$\begin{aligned} f(x_1 . x_2) =\frac{1}{1+e^{\frac{x_1 . x_2}{\beta }}} \end{aligned}$$
(11)
Fig. 1.
figure 1

Working of CS-LDMP

Full size image

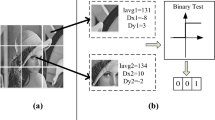
In Fig. 1 the calculation proceeds as follows,

$$ CS-LDMP_{8,1,f}=round((\frac{0.8807x2^0+0.9975x2^1+0.2689x2^2+1x2^3}{15})x15) = 12 $$

4.2 eXtended Center-Symmetric Local Mapped Patterns (XCS-LMP)

In this section, we propose to modify the threshold function of XCS-LBP operator which gives us a new operator XCS-LMP. Similar to the above method, we use the sigmoid function instead of a regular Heaviside function. It would appear that this method can capture minute differences between images, which the earlier XCS-LBP method could not accomplish.

The method of calculation is as follows. First, we calculate the \(g_1\) and \(g_2\) function values and then send the result to the sigmoid function. The results from the sigmoid function from different pairs of pixels are then multiplied with the weighing factors to produce a floating-point number. The result is divided by sum of weighing factors, and then it is rounded off to the nearest integer value. The value b is one less than the number of histogram bins. Equation 12 gives the mathematical model of XCS-LMP.

$$\begin{aligned} XCS-LMP_{(P,R,f)} (x,y) = round(\frac{\sum _{i=0}^{\frac{P}{2}-1} {f(g_1(i,c)+g_2(i,c))}2^i}{\sum _{i=0}^{\frac{P}{2} - 1} {2^i}})b \end{aligned}$$
(12)

where

$$\begin{aligned} f(x_1 + x_2) =\frac{1}{1+e^{\frac{-(x_1 + x_2)}{\beta }}} \end{aligned}$$
(13)
$$\begin{aligned} g_1(i,c) = n_i - n_{i + \frac{P}{2}} + n_c, g_2 (i,c) = (n_i - n_c)(n_{i + \frac{P}{2}} - n_c) \end{aligned}$$
(14)
Fig. 2.
figure 2

XCS-LMP

Full size image

In Fig. 2 the calculation proceeds as follows,

$$ XCS-LMP_{8,1,f}=round((\frac{0.0024x2^0+0.2689x2^1+0.7310x2^2+0.1192x2^3}{15})x15) = 3 $$

5 Experimental Results

Numerous experiments were conducted to illustrate the performances of both of the proposed operators. For coding purposes, we use Python 3.6 with the xgboost library on a Windows 10 OS equipped with Intel(R) Core(TM) i7-6700HQ CPU @ 2.60Ghz 2.60 GHz and 1600MHz DDR3L RAM. The dataset used is CIFAR10 as in A. Krizhevsky and G. Hinton [12]. They contain images of objects such as an airplane, bird, dog. We give the comparison of performances of the following operators: (i) CS-LBP (ii) CS-LDP (iii) CS-LMP (iv) CS-LDMP (v) XCS-LBP (vi) XCS-LMP

Fig. 3.
figure 3

Comparison of transformed images of a car starting with original image, CS-LBP, CS-LDP, CS-LMP, Proposed CS-LDMP, XCS-LBP, Proposed XCS-LMP from left to right

Full size image
Table 1. Accuracy table
Full size table

Color images of the CIFAR10 dataset are first converted to grayscale, for which luminance was used. The following formula for luminance given in C. Kanan and G. W. Cottrell [13] was used, that is, given in Eq. 15.

$$\begin{aligned} G_{luminance} = 0.3R + 0.59G +0.11B \end{aligned}$$
(15)

where \(R , G , and\, B\) are the intensity values of red, blue, and green, respectively. Secondly, we convert the original image to a different image using the local descriptor. Pixels are always compared in a clockwise fashion starting with the top left pixel. After that, we calculate the histogram of the transformed image and store it separately. Finally, we use the Xgboost algorithm as in T. Chen and C. Guestrin [14] for training the algorithm on the extracted features from the algorithm from the extracted features from the corresponding operator.

For analyzing the performances, three evaluation metrics were used: (i) accuracy, (ii) precision vs recall curve, and (iii) receiver operator characteristics curve (ROC Curve). ROC curve is simply the plot between true positive rate and false positive rate. The definitions of the terms are given in Eqs. 16, 17, 18, and 19.

$$\begin{aligned} Accuracy = \frac{TP +TN}{P + F} \end{aligned}$$
(16)
$$\begin{aligned} Precision = \frac{TP}{TP + FP} \end{aligned}$$
(17)
$$\begin{aligned} Recall = True Positive Rate = \frac{TP}{TP + FN} \end{aligned}$$
(18)
$$\begin{aligned} False Positive Rate = \frac{FP}{TN+FP} \end{aligned}$$
(19)
Fig. 4.
figure 4

Precision-recall curve for 1500 estimators

Full size image

where TP = No. of True Positives, TN = No. of True Negatives, P = No. of Positive examples, F = No. of Negative examples, FP = No. of False Positives, FN = No. of False Negatives. The above definitions would be valid for a binary classification problem. Since we would be doing a multi-class classification problem, we should be following a different strategy, i.e., micro-averaged evaluation metric as given in V. Van Asch [15]. Firstly, the accuracy table is given, followed by precision vs. recall curve (PR) and receiver operating characteristics curve (ROC) with the area under each curve (AUC). The PR curve and ROC curve are provided for a specific number of estimators of the xgboost library due to space constraints. Here, Est. indicates the number of estimators used in the xgboost classifier. In Fig. 3, transformed images of a car are given, by different operators.

Fig. 5.
figure 5

Receiver operating characteristics for 1500 estimators

Full size image

Now, performances are analyzed in the following order: accuracy, PR curve, ROC curve. The proposed CS-LDMP operator outperforms the CS-LBP, CS-LDP, and CS-LMP operators concerning accuracy as given in Table 1. When \(est = 800\), CS-LDMP’s accuracy is better than CS-LMP by 20%. Moreover, we can also see that the proposed XCS-LMP operator is giving slightly better accuracy than XCS-LBP operator, and hence better accuracies when compared with the other operators. Secondly, the Precision-Recall Curve in Fig. 4 is observed. It can be for plainly said that the proposed CS-LDMP outperforms CS-LBP, CS-LDP, and CS-LMP operators as the area under the curve (AUC) is greater by 20% with CS-LBP and CS-LMP and 5% higher than CS-LDP. Moreover, at any fixed recall, the precision of the proposed CS-LDMP is greater than CS-LBP, CS-LDP, and CS-LMP. Additionally, XCS-LMP is slightly better than XCS-LBP, which is 0.04 percent regarding AUC, and we can even say that when the recall value is small, precision of XCS-LMP appears to be greater than XCS-LBP. Finally, in the ROC curve as shown in Fig. 5, proposed CS-LDMP has AUC 2.5% more than CS-LBP and CS-LMP and 0.6% more than CS-LDP. However, the AUC of proposed XCS-LMP is very slightly less than XCS-LBP.

6 Conclusion

In this paper, two new local descriptors were presented, proposed CS-LDMP and XCS-LMP. CS-LDMP uses the advantages of CS-LDP and CS-LMP and therefore performs better than them. Therefore, trivially it performs better than CS-LBP. It captures more texture information by using the center pixel information, which is the strength of CS-LDP and captures minute differences between images as in CS-LMP. Proposed XCS-LMP uses the powers of XCS-LBP, robustness to noise, tolerance to illumination changes, and CS-LMP capturing nuances between images. Experimentally, we have shown that proposed CS-LDMP outperforms CS-LBP, CS-LDP, and CS-LMP concerning accuracy, AUC of PR curve and AUC of ROC curve. Additionally, proposed XCS-LMP has a slight improvement over XCS-LBP regarding the same.