Analytical Behavior of Rectangular Plates Under in-Plane and Lateral Dynamic Loads

Abstract

Analytical behavior of rectangular plates with semi-rigid boundary conditions under in-plane and lateral dynamic loads of constant thickness resting on the Winkler foundation is analyzed using a modified Bolotin method. The presentation of the semi-rigid isotropic plate’s frequency in a form analogous to the corresponding frequency of a simply supported plate is postulated, considering the wave numbers as unknown quantities. These two equations are determined from a system of two transcendental equations, obtained from the solution of two auxiliary Levy-type problems. The method was shown to be remarkably accurate when used to determine the natural frequencies of plates with non-simply supported boundary conditions. A natural extension of this research is related to the buckling and lateral vibration of isotropic plates subjected to in-plane forces which are time invariant and constant over the area of the plate, with their principal directions parallel to the plate edges and the dynamic lateral force. It is the purpose of this paper to illustrate this extension and to demonstrate its applicability by the presentation of numerical results for a particular plate.

Wiratman Wangsadinata—Deceased.

1 Introduction

The instability characteristics of isotropic rectangular concrete plate subjected to in-plane and lateral loads are utilized in many areas including engineering design and earthquake-resistant structures. Significant studies have been made by Viswanathan et al. in 2006 on buckling analysis of rectangular plates with variable thickness resting on elastic foundations [1]. The plate was homogeneous with the plate thickness varying using spline function approximation techniques. The plate is fully attached to the foundation. A pair of the rectangular plate’s opposite edges is subjected to compressive uniform load. Two cases of boundary conditions are considered for these edges: clamped–clamped and clamped–simply supported. The deflection equation yields an eigenvalue problem solving in which the critical loads and the mode shapes of buckling are obtained.

In the present work, the buckling of thin isotropic rectangular plates of constant thickness resting on elastic foundation is studied. The boundary condition that is considered for these edges is semi-rigid. The eigenvalue and eigenvector problems are solved by using the modified Bolotin method. The mode shapes of buckling are obtained from the transcendental equation.

Parametric studies of the variation of the critical load with respect to the aspect ratio, foundation stiffness, and variation of thickness of the plate are made. Selected mode shapes of buckling are also presented.

2 Formulation of the Problem

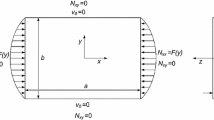
Consider a thin isotropic rectangular plate bounded by x = 0, x = a, y = 0, and y = b as shown in Fig. 1. The isotropic plate is subjected to the in-plane forces N _x and N _y acting on and normal to the edge x = 0; x = a; y = 0; and y = b. Its transverse deflection w(x, y, t) by using the classical plate theory is governed by the fourth-order partial differential equation as follows:

Fig. 1

Isotropic rectangular plate of thin plate on elastic foundation subjected to the in-plane forces

$$\begin{aligned} & D\left( {\frac{{\partial^{4} w(x,y,t)}}{{\partial x^{4} }} + 2\frac{{\partial^{4} w(x,y,t)}}{{\partial x^{2} \partial y^{2} }} + \frac{{\partial^{4} w(x,y,t)}}{{\partial y^{4} }}} \right) - N_{x} \frac{{\partial^{2} w(x,y,t)}}{{\partial x^{2} }} - N_{y} \frac{{\partial^{2} w(x,y,t)}}{{\partial y^{2} }} \\ & \quad + k_{f} w(x,y,t) + \rho h\frac{{\partial^{2} w(x,y,t)}}{{\partial t^{2} }} = p(x,y,t) \\ \end{aligned}$$

(1)

where w(x, y, t) is the transverse displacement of the plate; D is the flexural rigidity of the plate defined by

$$D = \frac{{Eh^{3} }}{{12\left( {1 - \nu^{2} } \right)}},$$

(2)

E is Young’s modulus; h is the plate thickness; k _f is the foundation stiffness; υ is Poisson’s ratio; N _x and N _y are normal forces per unit length of plate in the x- and y-directions, respectively, positive if in tension; and p(x, y, t) is the lateral dynamic load. The forces per unit length are related to the in-plane stresses (σ _x , σ _y , τ _xy ) by N _x  = σ _x h; N _y  = σ _y h and N _xy = τ _xy h. Let us assume N _y  = αN _x and N _xy  = 0 [2].

The isotropic plate is fully attached to the elastic foundation of elastic coefficient k _f . Let the edges x = 0; x = a; y = 0; and y = b be semi-rigid supported, then the boundary conditions can be expressed as follows.

At x = 0 and x = a:

$$w(x,y,t) = 0\,{\text{and}}\,D\left( {\frac{{\partial^{2} w(x,y,t)}}{{\partial x^{2} }} + \nu \frac{{\partial^{2} w(x,y,t)}}{{\partial y^{2} }}} \right) = k_{1} \frac{\partial w(x,y,t)}{\partial x}$$

(3)

At y = 0 and y = b:

$$w(x,y,t) = 0\,{\text{and}}\,D\left( {\frac{{\partial^{2} w(x,y,t)}}{{\partial y^{2} }} + \nu \frac{{\partial^{2} w(x,y,t)}}{{\partial x^{2} }}} \right) = k_{2} \frac{\partial w(x,y,t)}{\partial y}$$

(4)

Adopting the non-dimensional coordinates ξ = x/a; η = y/b, Eq. (1) becomes

$$\frac{{\partial^{4} w}}{{\partial \xi^{4} }} + 2s^{2} \frac{{\partial^{4} w}}{{\partial \xi^{2} \partial \eta^{2} }} + s^{4} \frac{{\partial^{4} w}}{{\partial \eta^{4} }} + \frac{{a^{4} \rho h}}{D}\frac{{\partial^{2} w}}{{\partial t^{2} }} + \frac{{a^{2} N_{x} }}{D}\left( {\frac{{\partial^{2} w}}{{\partial \xi^{2} }} + \alpha s^{2} \frac{{\partial^{2} w}}{{\partial \eta^{2} }}} \right) + \frac{{a^{4} k_{f} }}{D}w = 0$$

(5)

where s is the aspect ratio defined by a/b; α is the ratio between N _x /N _y .

A solution for the displacement w(ξ,η,t) can be expressed by:

$$w(\xi ,\eta ,t) = W_{mn} (\xi ,\eta )\cos \left( {\omega_{mn} t} \right) = X_{m} (\xi )Y_{n} (\eta )\cos \left( {\omega_{mn} t} \right)$$

(6)

where ω _mn is the natural frequency of the plate and W _mn (ξ, η) is the function of position coordinates determined for the mode numbers m and n in the ξ-direction and η-direction, respectively, which can be determined from the first and second auxiliary Levy-type problem [3].

3 Determination of the Eigenfrequencies

In order to solve the non-dimensional Eq. (5) of the problem, the free vibration solution of the problem is set as shown in Eq. (6) above.

3.1 First Auxiliary Levy-Type Problem

Based on the modified Bolotin method, the solution of Eq. (5) for the first auxiliary problem can be expressed in non-dimensional form as:

$$W_{mn} (\xi ,\eta ) = \sum\limits_{m = 1}^{m} {\sum\limits_{n = 1}^{n} {X_{mn} (\xi )\sin \left( {\pi q\eta } \right)} }$$

(7)

Satisfying the semi-rigid boundary conditions along ξ = 0 and ξ = 1:

$$X_{mn} (\xi ) = 0;\left( {\frac{{\partial^{2} W(\xi ,\eta )}}{{\partial \xi^{2} }} + \upsilon s^{2} \frac{{\partial^{2} W(\xi ,\eta )}}{{\partial \eta^{2} }}} \right) = - \overline{{k_{1} }} s\frac{\partial W(\xi ,\eta )}{\partial \xi }$$

(8)

where $\overline{{k_{1} }} = \frac{{k_{1} b}}{D}$ is the non-dimensional rotational stiffness coefficient that varies from 0 to 1.

Substituting Eq. (7) into Eq. (5) and satisfying the boundary conditions according to Eq. (8), the non-dimensional eigenvector in ξ-direction can be expressed as

$$X_{mn} (\xi ) = \sum\limits_{m = 1}^{m} {\sum\limits_{n = 1}^{n} {\cos \left( {p\pi \xi } \right) + F_{1} \sin \left( {p\pi \xi } \right) - \cosh (\beta \pi \xi ) + F_{2} \sinh (\beta \pi \xi )} }$$

(9)

where

$$\beta = \sqrt { - \frac{{s^{2} N_{0} }}{{\pi^{2} }} + p^{2} + 2s^{2} q^{2} }$$

(10)

$$\begin{aligned} F_{1} & = - \frac{{\beta \,\cos \left( {p\pi } \right)}}{{\beta \,\sin \left( {p\pi } \right) - p\,\sinh \left( {\pi \beta } \right)}} + \frac{{\beta \,\cosh \left( {\pi \beta } \right)}}{{\beta \,\sin \left( {p\pi } \right) - p\,\sinh \left( {\pi \beta } \right)}} \\ & \quad - \frac{{p^{2} \pi \,\sinh \left( {\pi \beta } \right)}}{{s\overline{{k_{1} }} \left( {\beta \,\sin \left( {p\pi } \right) - p\,\sinh \left( {\pi \beta } \right)} \right)}} - \frac{{\beta^{2} \pi \,\sinh \left( {\pi \beta } \right)}}{{s\overline{{k_{1} }} \left( {\beta \,\sin \left( {p\pi } \right) - p\,\sinh \left( {\pi \beta } \right)} \right)}} \\ \end{aligned}$$

(11)

$$\begin{aligned} F_{2} & = \frac{{p\,\cos \left( {p\pi } \right)}}{{\beta \,\sin \left( {p\pi } \right) - p\,\sinh \left( {\pi \beta } \right)}} - \frac{{p\,\cosh \left( {\pi \beta } \right)}}{{\beta \,\sin \left( {p\pi } \right) - p\,\sinh \left( {\pi \beta } \right)}} \\ & \quad + \frac{{p^{2} \pi \,\sin \left( {p\pi } \right)}}{{s\overline{{k_{1} }} \left( {\beta \,\sin \left( {p\pi } \right) - p\,\sinh \left( {\pi \beta } \right)} \right)}} + \frac{{\beta^{2} \pi \,\sin \left( {p\pi } \right)}}{{s\overline{{k_{1} }} \left( {\beta \,\sin \left( {p\pi } \right) - p\,\sinh \left( {\pi \beta } \right)} \right)}} \\ \end{aligned}$$

(12)

$$N_{0} = \frac{{b^{2} N_{x} }}{D}$$

(13)

3.2 Second Auxiliary Levy-Type Problem

The solution of Eq. (5) for the second auxiliary problem in non-dimensional form can be expressed as:

$$W_{mn} (\xi ,\eta ) = \sum\limits_{m = 1}^{m} {\sum\limits_{n = 1}^{n} {\sin \left( {\pi p\xi } \right)} } Y_{mn} (\eta )$$

(14)

Satisfying the semi-rigid boundary conditions along η = 0 and η = 1:

$$Y_{mn} (\eta ) = 0;\left( {\frac{{\partial^{2} W(\xi ,\eta )}}{{\partial \eta^{2} }} + \frac{\upsilon }{{s^{2} }}\frac{{\partial^{2} W(\xi ,\eta )}}{{\partial \xi^{2} }}} \right) = - \frac{{\overline{{k_{2} }} }}{s}\frac{\partial W(\xi ,\eta )}{\partial \eta }$$

(15)

where $\overline{{k_{2} }} = \frac{{k_{2} a}}{D}$ is the non-dimensional rotational stiffness coefficient that its value varies from 0 to 1.

Substituting Eq. (3) into Eq. (5) and satisfying the boundary conditions according to Eq. (15), the non-dimensional eigenvector in η-direction can be expressed as:

$$Y_{mn} (\eta ) = \sum\limits_{m = 1}^{m} {\sum\limits_{n = 1}^{n} {\cos \left( {q\pi \eta } \right) + F_{3} \sin \left( {q\pi \eta } \right) - \cosh (\theta \pi \eta ) + F_{4} \sinh (\theta \pi \eta )} }$$

(16)

where

$$\theta = \frac{1}{s}\sqrt {2p^{2} + s^{2} q^{2} - \frac{{s^{2} N_{0} \alpha }}{{\pi^{2} }}}$$

(17)

$$F_{3} = - \frac{{\overline{{k_{2} }} \theta \,\cos \left( {\pi q} \right) - \overline{{k_{2} }} \cosh \left( {\pi \theta } \right) + s\pi \left( {q^{2} + \theta^{2} } \right)\sinh \left( {\pi \theta } \right)}}{{\overline{{k_{2} }} \left( {\theta \,\sin \left( {\pi q} \right) - q\,\sinh \left( {\pi \theta } \right)} \right)}}$$

(18)

$$F_{4} = \frac{{\overline{{k_{2} }} q\,\cos \left( {\pi q} \right) - \overline{{k_{2} }} \cosh \left( {\pi \theta } \right) + s\pi \left( {q^{2} + \theta^{2} } \right)\sinh \left( {\pi q} \right)}}{{\overline{{k_{2} }} \left( {\theta \,\sin \left( {\pi q} \right) - q\,\sinh \left( {\pi \theta } \right)} \right)}}$$

(19)

The unknown quantities p and q which are the number of modes in the x- and y-directions for non-simply supported conditions are calculated from the transcendental equations:

$$\begin{aligned} & - 2s^{2} \overline{k}_{1}^{2} p\beta + 2s^{2} \overline{k}_{1}^{2} p\beta \,\cos \left( {p\pi } \right)\cosh \left( {\pi \beta } \right) \\ & \quad + \left( {s^{2} \overline{k}_{1}^{2} \left( {p^{2} - \beta^{2} } \right) + \pi^{2} \left( {p^{2} + \beta^{2} } \right)^{2} } \right)\sin \left( {p\pi } \right)\sinh \left( {\pi \beta } \right) = 0 \\ \end{aligned}$$

(20)

$$\begin{aligned} & - 2\overline{k}_{2}^{2} q\theta + 2\overline{k}_{2}^{2} q\theta \,\cos \left( {q\pi } \right)\cosh \left( {\pi \theta } \right) \\ & \quad + \left( {\overline{k}_{2}^{2} \left( {q^{2} - \theta^{2} } \right) + s^{2} \pi^{2} \left( {q^{2} + \theta^{2} } \right)^{2} } \right)\sin \left( {q\pi } \right)\sinh \left( {\pi \theta } \right) = 0 \\ \end{aligned}$$

(21)

Once the value of p and q are determined from Eqs. (20)–(21), the non-dimensional critical in-plane stresses for statics condition and the eigenvalues of the system can be expressed as

$$N_{0} = \frac{{p^{4} \pi^{4} + 2s^{2} p^{2} \pi^{4} q^{2} + s^{4} \left( {\overline{{k_{f} }} + \pi^{4} q^{4} } \right)}}{{s^{2} \pi^{2} \left( {p^{2} + s^{2} q^{2} \alpha } \right)}}$$

(22)

$$\overline{{\omega_{mn} }} = \sqrt {p^{4} \pi^{4} + s^{2} p^{2} \pi^{2} \left( { - N_{0} + 2\pi^{2} q^{2} } \right) + s^{4} \left( {\overline{{k_{f} }} + \pi^{4} q^{4} - N_{0} \pi^{2} q^{2} \alpha } \right)}$$

(23)

where $\overline{{k_{f} }} = \frac{{k_{f} a^{4} }}{{\pi^{4} D}}$ is non-dimensional Winkler foundation stiffness.

The eigenmodes of the system are determined as the product of Eqs. (9)–(16).

3.3 Determination of the Time Function

The time function for the system can be solved by using the Duhamel integration. It can be expressed as:

$$\ddot{T}_{mn} (t) + 2\xi \omega_{mn} \dot{T}(t) + \omega_{mn}^{2} T(t) = \frac{{\int\limits_{0}^{a} {X_{mn} (x)dx\int\limits_{0}^{b} {Y_{mn} (y)dy} } }}{{\rho hQ_{mn} }}P(t)\delta \left[ {x - \left( {x_{0} - \Delta xH\left( {t - t_{0} } \right)} \right)} \right]\delta \left[ {y - y_{0} } \right]$$

(24)

where Q _mn is the normalization factor of the eigenmodes that can be expressed as:

$$Q_{mn} = \int\limits_{0}^{a} {\left( {X_{mn} (x)} \right)^{2} } dx\int\limits_{0}^{b} {\left( {Y_{mn} (y)} \right)^{2} } dy$$

(25)

The lateral load, p(x, y, t), that moves suddenly from the initial position at x = x ₀ to the new position at x = x ₁ at time t = t ₀ can be expressed by using the Heaviside unit step function, H[.] [4].

Finally, the generalized dynamic deflection of the system can be solved by multiplying the spatial functions with the temporal function which is the solution of Eq. (24).

4 Numerical Applications, Results, and Discussion

Using the procedure described above, the concrete plate on the Winkler foundation subjected to the in-plane stresses in the x- and y-directions and the lateral load P(t) is analyzed. The plate is suddenly moved from the initial position at x = x ₀ to the new position at x = x ₁ at time t = t ₀. The structural properties of the plate are a = 3 m; s = a/b is varied from 1 to 2; the thickness, h is 0.12 m. The physical characteristics of the plate are ρ = 2400 kg/m³; E = 30.10⁹ N/m²; υ = 0.3; $\overline{{k_{f} }}$ = 1, $\overline{{k_{1} }}$ = 0.5; and $\overline{{k_{2} }}$ = 0.5. The non-dimensional in-plane stresses in the x-direction, N ₀ = 1; α = 1; the lateral load amplitude P ₀ = 10⁵ Nm/m². The initial position of the load at x ₀ = 0.3a, y ₀ = b/2, and t ₀ = 2 s.

4.1 Variation of Aspect Ratio Versus the Critical in-Plane Stress

Figure 2 shows the variation of aspect ratio as the function of the non-dimensional in-plane stresses for the rectangular plate with semi-rigid conditions at all edges. A rectangular plate as shown in Fig. 1 is compressed by in-plane stresses N ₀ along all of the four edges (α = 1). The smallest critical load is obtained for m = 1 and n = 1. Results from Eq. (22) are shown in Fig. 2, which shows that N ₀ = 19.7176.

Fig. 2

Non-dimensional critical buckling loads N ₀  = N _x b ²/D as a function of s = a/b for plate with semi-rigid conditions, $\overline{{k_{1} }} = \overline{{k_{2} }}$ = 0.5

The buckling loads displayed in Fig. 2 are critical values. That is, they are the lowest of the doubly infinite set of bucking eigenvalues that arise for each a/b. For 0.16 ≤ s ≤ 1, then m = 1; for 1 ≤ s ≤ 2, then m = 2; and for s > 2, then m = 3. The critical loads listed in Fig. 2 are only for the range of plate aspect ratios 0.16 ≤ s ≤ 3.

Increasing the aspect ratio s from s = 1 to s = 1.5 results in lowering the non-dimensional value of N ₀ as shown in Fig. 3. The foundation stiffness also plays a very important factor in increasing the value of the critical in-plane stresses.

Fig. 3

Non-dimensional value of N ₀ as a function of non-dimensional value of the foundation stiffness $\overline{{k_{f} }}$ for 2 values of s

4.2 Variation of Foundation Stiffness Versus the Maximum Dynamic Deflection

Figure 4 shows the non-dimensional foundation stiffness coefficient versus the maximum dynamic deflection computed using the value of N ₀  = 10 and $\overline{\omega }$ = 10 and 20. It can be seen from Fig. 3 that by increasing the foundation stiffness coefficient, the maximum dynamic deflection decreases for the value of load’s frequency $\overline{\omega }$ = 10; 20. It is also shown from Fig. 3 that the closer the value of load’s frequency to the value of the first natural frequency of the system, the higher the value of the maximum dynamic deflection.

Fig. 4

Graph of non-dimensional foundation stiffness versus maximum dynamic deflection for the value of s = 1; $\overline{{k_{1} }} = \overline{{k_{2} }}$ = 0.5; N ₀  = 10

4.3 Effect of in-Plane Stress and Lateral Load on Dynamic Deflection

Figure 5 shows the response spectra of the plate subjected to in-plane stresses in x- and y-directions and lateral load p(x, y, t). The lateral load is positioned initially at x = x ₀ and at time t = t ₀ before suddenly moved into a new position at x = x ₂. It can be seen that the maximum dynamic deflection is influenced by the value of N ₀. When the value of N ₀ approaches N _cr, the dynamic deflection will reach maximum value.

Fig. 5

Response spectra of the plate subjected to in-plane stresses and lateral load

Figures 5 and 6 show the various dynamic response of the plate subjected to in-plane stresses and lateral dynamic load that are suddenly moved to its new position for two different values of N ₀ . It can be seen that the dynamic response of the system is higher when the N ₀ is close to the value of N _cr . By increasing the value of in-plane stresses by 10 times for $\overline{\omega }$ = 20, the dynamic response of the system increased by 90.5% for the dynamic deflection. The dynamic response of the system also increased drastically when the frequency of the lateral load approaches the fundamental frequency of the system as shown in Fig. 4.

Fig. 6

Various dynamic response of plate subjected to in-plane stresses and lateral load for the value of s = 1; $\overline{{k_{1} }}$ = $\overline{{k_{2} }}$ = 0.5; α = 1 and $\overline{{k_{f} }}$ = 1

5 Conclusion

The foregoing work has shown how the modified Bolotin method is used to analyze the buckling and the forced vibrations of rectangular plate sitting on the elastic foundation having two opposite edges in semi-rigid conditions. The procedure may be applied to all possible combination of fixed, simply supported, semi-rigid, or free-edge conditions applied continuously along the edges of the plate.

Analytical solutions of the mode number in the x and in the y direction is solved by using two transcendental equations. The whole formulation in this work is based on the assumption that the boundary supports of the plate are semi-rigid with rotational restraint. This is a very realistic assumption, particularly for concrete plates, because one may find that rotational deformations exist along the joints.

Critical in-plane stresses for plates on the Winkler foundation increase linearly with the value of foundation parameter k _f . The load combination of the in-plane compressive stresses in the x- and y-directions as well as the transversal load drastically effects the maximum dynamic deflection of the system, especially when the value of the in-plane stresses converges to the critical value and when the frequency value of the load converges to the fundamental frequency of the system.

The stability and the dynamic analysis presented here would be quite useful for plate structural elements such as concrete plate pavements.