Truss Damage Detection Using Modified Differential Evolution Algorithm with Comparative Studies

Abstract

In this paper, an efficient numerical algorithm is developed for the damage detection of planar and space truss structures based on the modified differential evolution algorithm (mDE) and vibration data. For this purpose, the mathematical programming of the finite element based on the force method and the singular value decomposition technique is presented. The general equilibrium equations in which unknown member forces and reaction forces are taken into account are formulated. The compatibility equations in terms of forces are explicitly presented by using the singular value decomposition method. The modified differential evolution algorithm (mDE) is used as an optimization algorithm of damage detection. The objective function for damage detection is based on vibration data such as natural frequencies and mode shapes. The feasibility and efficiency of the present method are compared with a genetic algorithm (GA) and a particle swarm optimization (PSO) for example. The numerical results show that the proposed strategy based on force method using mDE and vibration data can provide a reliable tool on determining the sites and extents of multiple damages of truss structures.

1 Introduction

The identification of structural damage is an important part of the monitoring and repairing of structural systems during their functional age. In order to improve the safety and life expectancy of structures, it is necessary to detect the damage extents and sites. The damage assessment technique has drawn wide attention from various engineering fields such as aerospace, mechanical, and civil engineering applications. The proposed identification of structural damage prevents the deterioration in a structural system from the impact loads and the responses of the structure. For damage detection and structural health monitoring, techniques based on vibration data have been extensively used. Thus, the damage evaluation of structures has derived wide consideration from engineering fields.

The various computational techniques have been used to solve the damage detection problem such as genetic algorithm (GA), differential evolution algorithm (DE), and particle swarm optimization (PSO). Among non-gradient-based methods, GA has been used widely from damage detection field. The GA is a well-known global optimizer based on the Darwin’s theory of evolution and survival of the fittest and the natural process through reproduction [1]. It makes the mechanisms of biological evolution to perform optimization without information regarding the objective function. Generally, the GA has been shown to be solved various optimization problems through some basic concepts and operators. However, some research work has appeared that it is complex for the simple GA to solve the damage quantification problems properly. To achieve a better detection result, the various optimization algorithms were improved [2,3,4]. Krishnakumar [5] proposed the micro-genetic algorithm based on serial genetic algorithms [6], and Koh and Dyke [2] proposed the use of correlation-based damage detection methods for long-span cable-stayed bridge. Nobahari and Seyedpoor [7] proposed a modified genetic algorithm (MGA) to identify multiple damage and two new tools to recognize the actual damage correctly and rapidly. Also, he used the DE algorithm to solve the optimization problem for detecting actual sites and elements which was demonstrated by truss structures. The GA has discrete design variables, and new attempts based on continuous domain have been proposed such as PSO, DE, and ant colony optimization (ACO).

Turning to the problems of global optimization method, Storn and Price [8] proposed the differential evolution (DE) algorithm as a simple and powerful population-based stochastic method, which has an operation process similar to GA. In order to overcome the shortcomings of the non-gradient-based methods regarding computational time as well as of the gradient-based methods concerning solution accuracy, several variations of DE algorithm have been suggested. Pampara et al. [9] suggested a binary DE using trigonometric functions, in which experimental results indicate the effectiveness of the technique and the viability for the DE to operate in binary space. Zou et al. [10] proposed to solve constrained optimization problems using a modified differential evolution algorithm. Its own crossover rate and scale factor were adjusted using uniform distribution, and mutation phase was modified to enhance the convergence for unconstrained optimization problems. Concerning the damage detection, Vo-Duy et al. [11] used a strain energy-based method and an improved differential evolution algorithm to locate and quantify damage on the laminated composite plate. Also, Dinh-Cong et al. [12] proposed a two-stage damage identification method to identify the location and extent of multiple damages at individual layers in laminated composite beams using DE algorithm. Jena et al. [13] presented a damage detection technique combining analytical and experimental investigations on a cantilever aluminum alloy beam with a transverse surface crack. The damage location and assessment is the third stage and is formulated as a constrained optimization problem and solved using the proposed differential evolution algorithm.

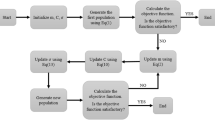
Based on the mentioned researches, the mDE has not yet been used as optimizer for 2D and 3D truss structures based on force method and vibration data until now. In this study, a mDE combined with the free vibration analysis is proposed as a highly efficient algorithm for performing the damage identification of truss structures. The introduced algorithm resolves efficiently the limitation of GA by randomly continuous design variables instead of discrete domain as in the GA. In order to solve the problem, the number of design variables and member types of truss structures are first defined. Design variables are randomly created in the range of lower and upper bounds based on the number of design variables. Consequently, based on the force method with the present mDE in the damage detection process, the results satisfying the required deficiencies of the force method and equilibrium matrices are selected.

2 Theoretical Modeling

In order to build a model for truss structure, the general equations and relations are briefly presented. Several approaches that are similar to those can be found in the literature [14, 15]. For a $d$-dimensional ($d$ = 2 or 3) truss structure with $m$ members, $n$ free nodes, and $n_c$ constrained nodes, its topology can be expressed by a connectivity matrix ${\mathbf {C}}_ s$ [16]. Let $r_c$ be the unknown vector of reaction forces employed to remove all boundary constraints. Therefore, the constrained nodes can now be treated as free nodes. In the context, the general equilibrium equations for all nodes (including constrained nodes) of the discrete truss can be written as follows:

$$\begin{aligned} \bar{\mathbf {A}}\bar{\mathbf {f}}=\bar{\mathbf {p}} \end{aligned}$$

(1)

where $\bar{\mathbf {A}}$ is called the general equilibrium matrix of all nodes, which transforms the vector of member and reaction forces $\bar{\mathbf {f}}$ to the vector of external loads $\bar{\mathbf {p}}$, $\bar{\mathbf {f}}$ is the unknown member and reaction force vector, and $\bar{\mathbf {p}}$ is the external load vector of all nodes.

In this study, the SVD method is used as an effective and numerically stable algorithm in order to extract $r$ compatibility conditions. The SVD is performed on the general equilibrium matrix $\bar{\mathbf {A}}$ instead of the kinematic matrix ${\mathbf {B}}$ (i.e., the transpose of the general equilibrium matrix $\bar{\mathbf {A}}$). The compatibility equations expressed in terms of forces are obtained as follows:

$$\begin{aligned} \mathbf {D}\bar{\mathbf {f}}={\mathbf {p}_{e_o}} \end{aligned}$$

(2)

where $\mathbf {D}$ is the compatibility matrix in terms of forces of all members and ${\mathbf {p}_{e_o}}$ is the virtual force vector in the indeterminate truss caused by member initial elongations ${\mathbf {e}_o}$.

For the free vibration analysis, the extended equation of motion based on the force method can be written as

$$\begin{aligned} \bar{\mathbf {M}}\ddot{\bar{\mathbf {d}}}+\tilde{\mathbf {A}}\bar{\mathbf {f}}=0 \end{aligned}$$

(3)

where $\bar{\mathbf {M}}$ is the extended mass matrix, $\ddot{\bar{\mathbf {d}}}$ is the extended acceleration vector, and $\tilde{\mathbf {A}}$ is the square full-rank matrix coupling the general equilibrium matrix and the compatibility matrix. For this analysis case, it is assumed that element forces are harmonics in time, $\bar{\mathbf {f}}$ = $\bar{\mathbf {F}}$sin($\omega$t), where $\omega$ and $\bar{\mathbf {F}}$ are the circular frequency and corresponding force mode shape, respectively. Therefore, equation [14] can be written as the following eigenvalue problem

$$\begin{aligned} (\tilde{\mathbf {A}}+\omega ^2\mathbf {B})\bar{\mathbf {F}}=0 \end{aligned}$$

(4)

where

$$\begin{aligned} \mathbf {B}=\bar{\mathbf {M}}{\tilde{\mathbf {A}}^{-T}}\mathbf {G} \end{aligned}$$

(5)

and ${\bar{\mathbf {M}}}$ is the extended mass matrix.

3 Structural Damage Detection

To determine the location and extent of the damages more accurately, the natural frequency and the mode shape changes are demanded ${messina_structural_1998,wang_structural_2001}$. In this study, the objective function based on the sum of two formulations is given as follows:

$$\begin{aligned} f (\text{ X }) = f_1(\text{ X }) + f_2(\text{ X }) \end{aligned}$$

(6)

where

$$\begin{aligned} {f_1}(\mathrm{{X}}) = \sum \limits _{i = 1}^n {\frac{{\left| {{\omega _{di}} - {\omega _i}(\mathrm{{X}})} \right| }}{{{\omega _{di}}}}} \end{aligned}$$

(7)

and

$$\begin{aligned} {f_2}(\mathrm{{X}}) = \sum \limits _{i = 1}^n {\sum \limits _{j = 1}^m {\left\| {\frac{{{\Phi _{dj}} - {\Phi _j}(\mathrm{{X}})}}{{{\Phi _{dj}}}}} \right\| } } \end{aligned}$$

(8)

where ${\omega _{i}}$ is the corresponding hypothesis natural frequency which is can be expected from analytic model and ${\omega _{di}}$ is the ith natural frequency of the damaged truss. ${\Phi _{dj}}$ and ${\Phi _j(X)}$ are the jth component of the ith damaged force eigenvector and the jth component of the ith hypothesis force eigenvector, respectively, in ${f}_2$(X). Then, the optimal design problem for damage identification of the truss structure is formulated as follows:

$$\begin{aligned} \begin{aligned} \text {Minimize}~~~~f(X)+\gamma g(X) \\ \end{aligned} \end{aligned}$$

(9)

in which

$$\begin{aligned} \begin{aligned} g(X)=(n_d-n_h)^2~~~~\text {for}~~ n_d>n_h \end{aligned} \end{aligned}$$

(10)

where $x_{i}$ is the damaged elastic modulus of the ith member, $\gamma$ is the penalty parameter, ${n_d}$ and ${n_h}$ are the number of the damaged elements and the number of the healthy elements, respectively. In real life, the healthy members are more than the damaged members in structures. Thus, both algorithms in this study can be accelerated to find better solution using the penalty function ${g(X)}$. In many researches related to the damage detection problem, the damage has been simulated by decreasing one of the stiffness parameters of the element. In this study, the damage of truss structures is simulated by the reduction in the elasticity modulus in each element as

$$\begin{aligned} x_{i}=\frac{E-E_{i}}{E},~~~~~~{i}=1,\dots ,n \end{aligned}$$

(11)

where E is the initial elastic modulus and $E_{i}$ is the final elastic modulus of nth element.

4 Optimization Algorithm

4.1 Differential Evolution Algorithm

Differential evolution (DE) has been first proposed by Storn and Price [8] as a vector-based metaheuristic algorithm. The DE has similarity to genetic algorithms, its use of selection, crossover, and mutation. The DE is a stochastic search algorithm with self-organizing tendency and does not use the information of derivatives [17]. Thus, it is a population-based, derivative-free method. In addition, DE uses real numbers as solution strings, so no encoding and decoding is needed. The main procedure of DE includes mutation, crossover, selection, and initialization of design variables.

4.1.1 Initialization

In the DE algorithm, ${d}$-dimensional real number of design variable vectors is randomly generated as much as population size for global optimum point. The ith vector of the population at any iteration can be expressed by conventional notation as

$$\begin{aligned} X_{i}=\{x_{i,1},x_{i,2},\cdots ,x_{i,d}\} \end{aligned}$$

(12)

where $X_i$ is a vector at ith population and ${d}$ is a number of design variables in $X_i$ vector. It is noted that this vector, called target vector, can be considered as chromosomes. A ${d}$-dimensional vector represents a candidate result to the problem and is randomly made in the domain as follows:

$$\begin{aligned} x_{i,j}=x_{\text {min},j}+rand\times (x_{\text {max},j}-x_{\text {min},j}),~~i=1,\overline{\text {NP}},~~j=1,\bar{n} \end{aligned}$$

(13)

where NP is the population size, $n$ is the number of design variables or dimensions, $rand$ is a uniformly distributed random number in the interval [0,1], $x_{i,j}$ is the jth component of individual $\mathbf x_i$, and $x _{\text {min},j}$ and $x _{\text {max},j}$ are the lower and upper bounds of $x _{j}$, respectively.

4.1.2 Mutation

In the mutation step, DE generates a mutant vector $\mathbf{{v}}_i$ based on the target vector $\mathbf{{x}}_{r_1}$ by using mutation operation at the current iteration. The frequently used some mutation schemes are introduced as below:

$$\begin{aligned} {\mathbf{{v}}_i} = \mathbf{{x}}_{r_1} + F \times (\mathbf{{x}}_{r_2}-\mathbf{{x}}_{r_3}) \end{aligned}$$

(14)

where $\mathbf{{v}}_i$ is a mutation vector and known as a new candidate solution; $\mathbf{{x}}_{r_1}$, $\mathbf{{x}}_{r_2}$, and $\mathbf{{x}}_{r_3}$ are candidate solutions; $r_1$, $r_2$, and $r_3$ are randomly determined from [1, NP] to satisfy the constraints as $r_1$ $\ne$ $r_2$ $\ne$ $r_3$ $\ne$ $i$; the scale factor $F$ can be selected within the range $F$ $\in$ [0, 2].

4.1.3 Crossover

In the crossover process, trial vector $\mathbf{{u}}_i$ is created by combining the target vector $\mathbf{{x}}_{i}$ and the mutant vector $\mathbf{{v}}_{i}$. The combination of these vectors in this process is controlled by a crossover ratio (CR) chosen in the range [0,1]. The CR controls how likely it is that each component of $\mathbf{{u}}_{i}$ comes from the mutant vector $\mathbf{{v}}_{i}$ and is defined by user. The range [0.1,0.8] or 0.5 can get good result at the beginning.

The crossover phase is generally performed two schemes: binomial and exponential. Due to its simplicity, the binomial crossover is employed and defined as follows:

$$\begin{aligned} {u_{i,j}} = \left\{ {\begin{array}{*{20}{l}} {{{v}_{i,j}},~~~~{\text {if}}~(ran{d_{i,j}} < CR)~{\text {or}}~(j = {j_{rand}})}\\ {{x_{i,j}},~~~~\text {otherwise}} \end{array}} \right. \end{aligned}$$

(15)

in which $rand_{i,j}$ is a uniformly distributed random number [0,1] and $j_{rand}$ is the integer chosen from [0,1].

4.1.4 Selection

Finally, the $\mathbf{{u}}_i$ and $\mathbf{{x}}_i$ vectors are compared so that the most fit vector in each pair is kept for the next generation and the least fit is discarded. This selection process is essentially the same as that used in GA and expressed as

$$\begin{aligned} \mathbf{{x}}_i^{new} = \left\{ {\begin{array}{*{20}{l}} {{\mathbf{{u}}_{i}},~~~~{\text {if}}~f({\mathbf{{u}}_i}) \le f({\mathbf{{x}}_i})}\\ {{\mathbf{{x}}_i},~~~~{\text {otherwise}}} \end{array}} \right. \end{aligned}$$

(16)

where $f$($\mathbf{{u}}_{i}$) and $f$($\mathbf{{x}}_{i}$) are the objective functions.

4.2 A Modified Differential Evolution Algorithm

In this section, mutation and selection phases are modified to overcome the drawbacks of the non-gradient- and gradient-based algorithms.

4.2.1 Modification of the Mutation Phase

Two mutation operators are adaptively chosen based on the absolute value of deviation of objective function between the best individual and the entire population in the previous generation (denoted as delta). More specifically, the value of delta is defined by

$$\begin{aligned} delta = \left| \frac{f_{mean}-f_{best}}{f_{best}} \right| \end{aligned}$$

(17)

where $f_{mean}$ is the mean objective function value of the whole population and $f_{best}$ is the objective function value of the best individual. The new mutation scheme is described as follows:

$$\begin{aligned} \mathbf{{v}}_i = \left\{ {\begin{array}{*{20}{l}} {\mathbf{{x}}_{best}+F^k \times (\mathbf{{x}}_{r_1}-\mathbf{{x}}_{r_2})},~~~~{\text {if}}~~ {delta > threshold} \\ {\mathbf{{x}}_{r_1}+F^k \times (\mathbf{{x}}_{r_2}-\mathbf{{x}}_{r_3})},~~~~~~{\text {otherwise}} \end{array} } \right. \end{aligned}$$

(18)

where $F^k$ is a number randomly chosen in [0,1] at the kth iteration; threshold is a criterion value which is chosen based on the stopping criterion of the algorithm.

Fig. 1

Two- and three-dimensional truss structures

Table 1 Induced elastic modulus for 31-bar planar truss

4.2.2 Modification of the Selection Phase

In the DE’s selection, the vectors are compared and unselected individual is worse than its target individual in the pair, but it can be still better than other individuals in the entire population. Consequently, several good information of unselected individuals can be omitted and the convergence speed of the DE algorithm is slow. The good individuals are kept for the next iteration as follows:

$$\begin{aligned} \mathbf{Q}=\mathbf{P}\cup \mathbf{U} \end{aligned}$$

(19)

where $\mathbf P$ and $\mathbf U$ are populations consisting of NP individuals $\mathbf{{x}}_{i}$ and $\mathbf{{u}}_{i}$ with i = 1, $\overline{\text{ NP }}$, respectively; $\mathbf Q$ includes all individuals of $\mathbf P$ and $\mathbf U$. Then, NP best individuals in $\mathbf Q$ are chosen to create a new population for the next iteration. Thus, the best solutions of the whole population are always stored for the next generation and the convergence rate is significantly improved.

Fig. 2

Convergence history of the 31-bar planar truss

5 Numerical Examples

In this section, two- and three-dimensional truss structures are investigated using GA, PSO, and proposed mDE algorithm. The searching process of these algorithms will be stopped when the maximum number of iterations is reached. In all examples, the crossover ratio (CR) for the proposed mDE and GA is set to be 0.6 and 1.0, respectively. Accordingly, all populations have to perform a crossover operation at all generation and there is no use of mutation process. The first three natural frequencies and mode shapes are used for detection. mDE algorithm and PSO find solution in a continuous domain, while results gained by GA are done in a discrete domain. The numerical results obtained by mDE are compared to GA and PSO to illustrate the accuracy and effectiveness of the proposed algorithm.

5.1 31-Bar Planar Truss

The first example is a 31-bar planar truss as shown in Fig. 1 and is modeled using 28 consistent finite elements without internal nodes leading to 25 degrees of freedom. The elasticity modulus $E =$ 70 GPa, the mass density $\rho$ = 2,770 kg/m$^3$, and the area of cross section A = 0.01 m$^2$. For every algorithms, the maximum number of iterations and population size are respectively set to be 500 and 300. In damage case, as damage ratios, the stiffness reduction in elasticity modulus 0.475 and 0.319 is induced at elements 8 and 16, respectively. The detected damages are shown by comparing the ratios of elasticity modulus reduction in GA, PSO, and mDE. Here, GA is considered with four different step points dq = 0.1, 0.05, 0.01, and 0.001.

Table 2 Induced elastic modulus for 25-bar space truss

The obtained results are expressed in Table 1 in comparison with each step points of GA and PSO. From this table, the damage location and extent of proposed algorithm were successfully determined than other cases of GA and agree well with this acquired by PSO. In a narrow discrete domain of search space, GA cannot find exact damage. Thus, GA have some difficulties about the accuracy of the solution if real solutions have many digits after the decimal point. Figure 2 shows the comparison of the convergence of each cases of GA, PSO and mDE at the whole iterations. As shown in the figure, mDE converges faster and lower than GA. For more detail, the mDE converges in 00 iterations with an objective function $f (\text{ X })=3.86 \times 10^{-11}$ in the first damage case, while each step point of GA converges $1.86 \times 10^{-2}$, $6.62 \times 10^{-3}$, $4.19 \times 10^{-2}$, and $1.41 \times 10^{-1}$ corresponding step points 0.1, 0.05, 0.01 and 0.001, respectively.

Fig. 3

Convergence history of the 25-bar space truss

5.2 25-Bar Space Truss

The 25-bar space truss is shown in Fig. 1, with 10 nodes leading to 18 degrees of freedom. The area of cross section A = 0.25 m$^2$, the material density $\rho$ = 7,830 kg/m.$^3$, and the modulus of elasticity E = 210 GPa. Likewise, the maximum number of iterations and population size are, respectively, set to be 500 and 300.

As a case of damage, the stiffness reductions in elasticity modulus 0.383 and 0.294 are induced at elements 6 and 16, respectively. The results gained by this example in comparison with the GA and PSO are presented in Table. 2. It can be seen that the present algorithm has shown excellent performance for damage detection than all step points of GA and agrees well with the result of PSO. When the step point increases, the gained results of GA are less accurate. Moreover, the convergence history of GA, PSO, and mDE are shown in Fig. 3. It demonstrates that mDE converges even faster than GA. Specially, mDE converges as $2.80 \times 10^{-11}$, while each step point of GA converges as $3.37 \times 10^{-2}$, $2.05 \times 10^{-1}$, $1.34 \times 10^{-1}$, and $8.65 \times 10^{-1}$ corresponding to step points dq = 0.1, 0.05, 0.01, and 0.001, respectively, and the value of converged objective function from PSO is $9.76 \times 10^{-7}$.

6 Conclusion

This study proposed the optimization technique which properly determines the locations and extents of multiple damages of planar and space trusses based on the modified differential evolution (mDE) algorithm with comparative studies. To generate the compatibility conditions for indeterminate trusses, the singular value decomposition technique is employed on the general equilibrium equations. The force mode vectors are introduced as eigenvectors in the objective function. The optimization problem has been solved using mDE which has continuous design variables to identify the actual damages. Three illustrated test examples such as planar and space trusses are considered in order to assess the performance of the proposed method. Throughout the numerical examples, the relative performance of mDE, GA, and PSO in the damage detection of trusses is studied. Numerical results show that the combination of the present force method and mDE is far more efficient than PSO and GA with discrete design variables for identifying multiple damages of trusses.