Nonlinear Tracking Control for Image-Based Visual Servoing with Uncalibrated Stereo Cameras

Abstract

This paper considers the problem of uncertain camera pose and camera parameters for a 3-degree-of-freedom (DOF) robot manipulator in nonlinear visual servoing tracking control. To solve this problem, the typical Kalman filter (KF) algorithm is designed to estimate the image Jacobian matrix online, which can reduce the system noises to improve the robustness of the control system. Visual optimal feedback controller is developed to precisely track the desired position of the robot manipulator. In addition, stereo cameras are incorporated into the robot manipulator system such that the tracking errors in both camera image frame and robot base frame can simultaneously converge to zero. Experimental results are included to illustrate the effectiveness of the proposed approach.

1 Introduction

Visual servoing has been generally used in robot manipulator nonlinear tracking control. The traditional robot hand-eye coordination control theories rely on the study of camera calibration technique. However, the calibration accuracy restricts the accuracy of system in practice. The camera pose can be changed and sometimes its working condition can be difficult to realize calibration. Compared with known camera parameters, uncalibrated visual servo system performs higher flexibility and adaptability.

Several visual servoing control methods have been developed to improve the control performance of robot manipulator. Chaumette presented a summary of visual servo control approaches [1]. Farrokh investigated the comparison of the position-based and image-based robot visual servoing methods to improve the dynamics performance and robustness of visual servoing (RVS) system [2]. In [3], it was mentioned that image-based visual servoing (IBVS) is a properer way under the condition of unknown camera parameters. Cai presented a 2-1/2-D visual servoing choosing orthogonal image features to enhance the behavior of tracking system [4]. The image Jocabian matrix, first presented by Weiss, is universally utilized to define the relationship between camera image frame and robot base frame. Zergerogluprovided the analytic solution of the image Jacobian matrix under the condition of ideal camera pose for the problem of position tracking control of a planar robot manipulator with uncertain robot-camera parameters [5]. While in practice, it is impossible to guarantee that the camera imaging plane is parallel to the task plane, that is, the relationship between the two coordinate systems cannot only be defined by one rotation angle. Hence, the control methods based on the direct estimation for the numerical solution of the image Jacobian matrix are widely used in robot hand-eye coordination research field. In [6], discrete-time estimator was developed by using the least squares algorithm. Yoshimi utilized geometric effect and rotational invariance to accomplish alignment [7]. Piepmeier performed online estimation using a dynamic recursive least-squares algorithm [8], while the work [9] addressed robust Jacobian estimation.

In this paper, the nonlinear visual servo controller is developed for a 3-degree-of-freedom (DOF) robot manipulator with fixed uncalibrated stereo cameras configuration. Only one-step robot movement is used to estimate the current image Jacobian matrix completely using Kalman filter (KF) algorithm. Furthermore, the filtering process adopts recursive computing without storing historical data. Then, a simple visual optimal feedback control is designed to achieve nonlinear trajectory tracking.

2 Problem Formulation

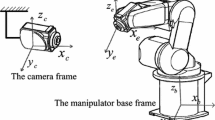
The visual sensor is used to measure the information in robot task space, and intuitively reflects the relationship between the robot end-effector and the target to be tracked. According to [10], the mapping relation between camera image frame and robot base frame is defined as follows:

$$ \dot{s} = J_{I} \left( p \right) \cdot \dot{p} $$

(1)

where $p\left( t \right) = \left( {x_{b} \left( t \right)\;\;y_{b} \left( t \right)} \right)^{\rm T}$ denotes the end-effector position in robot base frame, $s\left( t \right) = \left( {u_{l} \left( t \right)\;\;v_{l} \left( t \right)\;\;u_{r} \left( t \right)\;\;v_{r} \left( t \right)} \right)^{\rm T}$ represents the projected position of the end-effector in stereo camera image frame. The image Jacobian matrix, expressed by $J_{I} \left( q \right) \in {\mathbb{R}}^{4 \times 2}$, is defined as

$$ J_{I} \left( p \right) = \frac{\partial s}{\partial p} = \left( {\begin{array}{*{20}l} {\frac{{\partial u_{l} }}{{\partial x_{b} }}} \hfill & {\frac{{\partial u_{l} }}{{\partial y_{b} }}} \hfill \\ {\frac{{\partial v_{l} }}{{\partial x_{b} }}} \hfill & {\frac{{\partial v_{l} }}{{\partial y_{b} }}} \hfill \\ {\frac{{\partial u_{r} }}{{\partial x_{b} }}} \hfill & {\frac{{\partial u_{r} }}{{\partial y_{b} }}} \hfill \\ {\frac{{\partial v_{r} }}{{\partial x_{b} }}} \hfill & {\frac{{\partial v_{r} }}{{\partial y_{b} }}} \hfill \\ \end{array} } \right) $$

(2)

where $J_{I} \left( p \right)$ is the interaction matrix involving the end-effector position and the intrinsic and extrinsic parameters of cameras. Specifically, the corresponding spatial position can be uniquely determined from the image feature, because the dimension of image feature space is greater than the dimension of robot motion space, which means that the tracking of image space is equivalent to the tracking of robot motion space with stereo cameras configuration.

3 Online Estimation and Visual Optimal Feedback Controller

3.1 Online Estimation

To estimate the image Jacobian matrix online via KF, transforming the image Jacobian matrix into a state vector which can be expressed as the following form:

$$ x = \left( {\begin{array}{*{20}l} {\frac{{\partial s_{1} }}{\partial p}} \hfill & {\frac{{\partial s_{2} }}{\partial p}} \hfill & {\frac{{\partial s_{3} }}{\partial p}} \hfill & {\frac{{\partial s_{4} }}{\partial p}} \hfill \\ \end{array} } \right)^{\rm T} $$

(3)

where $\frac{{\partial s_{i} }}{\partial p} = \left( {\begin{array}{*{20}c} {\frac{{\partial s_{i} }}{{\partial x_{b} }}} & {\frac{{\partial s_{i} }}{{\partial y_{b} }}} \\ \end{array} } \right)^{\rm T}$,$i = 1,2,3,4$,denotes the transposition of $i$ th row vector of the image Jacobian matrix $J_{I} \left( p \right)$.

Based on the definition of $J_{I} \left( p \right)$ in (1), $s$ can be written as

$$ s\left( {k + 1} \right) \approx s\left( k \right) + J_{I} \left( k \right) \cdot \Delta p\left( k \right) = s\left( k \right) + J_{I} \left( k \right) \cdot u\left( k \right) $$

(4)

We define $x$ in (3) as the system state, and the image feature variation $\Delta s\left( k \right) = s\left( {k + 1} \right) - s\left( k \right)$ as the system output $z\left( k \right)$. Hence, the state equation can be derived as follows:

$$ x\left( {k + 1} \right) = x\left( k \right) + \eta \left( k \right) $$

(5)

$$ z\left( k \right) = C\left( k \right) \cdot x\left( k \right) + w\left( k \right) $$

(6)

where $\eta \left( k \right) \in {\mathbb{R}}^{8}$ denotes the state noise and $w\left( k \right) \in {\mathbb{R}}^{4}$ is the observation noise, which are both assumed to be white Gaussian noises shown in (7).

$$ \begin{aligned} & E\left( {\eta \left( k \right)} \right) = 0,\;\;\text{cov} \left\{ {\eta \left( k \right),\eta \left( j \right)} \right\} = R_{\eta } \cdot \delta_{kj} \\ & E\left( {w\left( k \right)} \right) = 0,\;\;\text{cov} \left\{ {w\left( k \right),w\left( j \right)} \right\} = R_{w} \cdot \delta_{kj} \\ & \text{cov} \left\{ {\eta \left( k \right),w\left( j \right)} \right\} = 0 \cdots \forall k,j \\ \end{aligned} $$

(7)

The system input of the state Eqs. (5) and (6) is contained in $C\left( k \right)$:

$$ C\left( k \right) = \left( {\begin{array}{*{20}c} {u^{\rm T} \left( k \right)} & {} & 0 \\ {} & \ddots & {} \\ 0 & {} & {u^{\rm T} \left( k \right)} \\ \end{array} } \right)_{4 \times 8} $$

(8)

Five steps of recursive estimation based on KF algorithm are listed as follows:

Step 1. Predict the next state based on current state

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} \left( k \right) = x\left( {k + 1|k} \right) = x\left( {k|k} \right) $$

(9)

Step 2. Update the uncertainty with respect to the state estimate

$$ P\left( {k + 1|k} \right) = P\left( {k|k} \right) + R_{\eta } $$

(10)

Step 3. The Kalman gain can be computed as

$$ K\left( {k + 1} \right) = P\left( {k + 1|k} \right) \cdot C^{\rm T} \left( k \right) \cdot [C\left( k \right) \cdot P\left( {k + 1|k} \right) \cdot C^{\rm T} \left( k \right) + R_{w} ]^{ - 1} $$

(11)

Step 4. The optimal state estimate value is given by

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} \left( {k + 1} \right) = x\left( {k + 1|k + 1} \right) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} \left( k \right) + K\left( {k + 1} \right) \cdot [z\left( {k + 1} \right) - C\left( k \right) \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} \left( k \right)] $$

(12)

Step 5. Update the state covariance matrix

$$ P\left( {k + 1|k + 1} \right) = [I - K\left( {k + 1} \right) \cdot C\left( k \right)] \cdot P\left( {k + 1|k} \right) $$

(13)

Given any two-step linearly independent test movement $\Delta p_{1} ,\Delta p_{2}$, the corresponding image feature variations $\Delta s_{1} ,\Delta s_{2}$ are gained. Thus, the initial value of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} \left( 0 \right)$ (i.e. $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J}_{I} \left( 0 \right)$) can be obtained:

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J}_{I} \left( 0 \right) = \left( {\Delta s_{1} \;\;\Delta s_{2} } \right) \cdot \left( {\Delta p_{1} \;\;\Delta p_{2} } \right)^{ - 1} $$

(14)

where $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} \left( 0 \right)$ can be remodeled by $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J}_{I} \left( 0 \right)$ using the form in (3).

3.2 Visual Optimal Feedback Controller Design

After online estimation of the image Jacobian matrix, the design of the direct visual feedback controller can be easily established. Define the system error in camera image frame as:

$$ e\left( t \right) = s^{ * } \left( t \right) - s\left( t \right) $$

(15)

where $s^{ * } \left( t \right) = s_{o} \left( t \right)$ denotes the desired image feature describing the image feature of the moving target.

The control objective of this paper is to design a control signal $u = \dot{p}$, which minimize the following objective function

$$ H = \frac{1}{2}e^{\rm T} e $$

(16)

Discretizing the control signal $u$, the optimal control signal at time $k$ is given by

$$ u\left( k \right) = J_{I} \left( k \right)^{ + } \cdot \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{o} \left( {k + 1} \right) - s\left( k \right)} \right) $$

(17)

where $J_{I} \left( k \right)^{ + }$ is Moore–Penrose pseudoinverse of $J_{I} \left( k \right)$.When $J_{I} \left( k \right)$ is of full rank 2, its inverse can be expressed as

$$ J_{I} \left( k \right)^{ + } = \left( {J_{I} \left( k \right)^{\rm T} J_{I} \left( k \right)} \right)^{ - 1} J_{I} \left( k \right)^{\rm T} $$

(18)

The estimation of $k + 1$, denoted by $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{o} \left( {k + 1} \right)$, can be obtained by

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{o} \left( {k + 1} \right) = s_{o} \left( k \right) + \left( {s_{o} \left( k \right) - s_{o} \left( {k - 1} \right)} \right) $$

(19)

Theorem 1

With the configuration of stereo cameras, the control law ( 17 ) guarantees global asymptotic position tracking at any time $k$.

$$ e_{p} \left( k \right) = p^{ * } (k) - p(k) \to 0 $$

(20)

Proof

Substituting (4), (17) and (19) into (16), the objective function is rewritten as the following form:

$$ \begin{aligned} H\left( k \right) & = \frac{1}{2}\left( {s^{ * } \left( k \right) - s\left( k \right)} \right)^{\rm T} \left( {s^{ * } \left( k \right) - s\left( k \right)} \right) \\ & = \frac{1}{2}\left( {s_{o} \left( k \right) - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{o} \left( k \right)} \right)^{\rm T} \left( {s_{o} \left( k \right) - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{o} \left( k \right)} \right) \\ & = \frac{1}{2}\sum\limits_{i = 1}^{4} {\left( {s_{oi} \left( k \right) - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{oi} \left( k \right)} \right)^{2} } \to 0 \\ \end{aligned} $$

(21)

From (21), the difference between the target image feature and its estimation tends to zero via KF algorithm. Under stereo cameras configuration, the convergence of image space is equivalent to the convergence of robot motion space with stereo cameras configuration. Hence, the conclusion of (20) is straightforward. In Eye-to-hand system, the control signal $u\left( k \right)$ is able to guarantee the asymptotic convergence of tracking error.

4 Experimental Verification

In this section, a 3-DOF robot manipulator system is employed as the test-rig to test the proposed control scheme. The configuration of the whole experimental setup is depicted in Fig. 1. The experimental setup is composed of a YASKAWA 6-DOF robot manipulator (rotation part is locked), two fixed pinhole cameras and an upper computer. The control method is written by using Visual C ++ program. The camera frame rate is set as 30 fps.

Fig. 1

A 3-DOF visual robot manipulator test-rig

The robot end-effector performs two-dimensional translation movement, tracking the curve track target on task plane, and uncalibrated stereo cameras are fixed right above the task plane.

The linearly independent test movements lead to the initial state vector is given by

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J}_{I} \left( 0 \right) = \left( {\begin{array}{*{20}c} {3.7608} & {0.0081} & {2.4344} & { - 0.0035} \\ { - 4.0446} & { - 2.3378} & { - 0.4403} & { - 2.4993} \\ \end{array} } \right)^{\rm T} $$

(22)

The variance of the each noise in the state equation and the covariance matrix is set to

$$ R_{\eta } = 0.2 \cdot I_{8} \;\;\;R_{w} = 0.2 \cdot I_{4} \;\;\;P\left( 0 \right) = 15 \cdot I_{8} $$

(23)

Experimental results are shown in Figs. 2 and 3. Figure 2a describes the tracking result of the left camera, Fig. 2b gives the tracking results of the right camera. Figure 3 shows the tracking errors of the left camera and the right camera, respectively. From Figs. 2 and 3, it is found that the output can precisely track the desired trajectory and the tracking errors can converge to zero. Hence, one can conclude that the aforementioned results successfully illustrate that effectiveness of the proposed visual optimal feedback control method.

Fig. 2

Desired trajectory and end-effector trajectory in camera image frame

Fig. 3

Tracking errors in camera image frame

5 Conclusions

In this paper, online estimation of the image Jacobian matrix has been investigated using uncalibrated stereo cameras. This method, which combines KF algorithm and visual optimal feedback control, is presented for a 3-DOF robot manipulator with system noises. KF is utilized to estimate the image Jacobian matrix, and the visual optimal feedback control is designed based on the estimate values. Stereo cameras system is applied to guarantee tracking error converging to zero. Experimental results verify the effectiveness and robustness of the proposed algorithm.