Adaptive Robust Control for a Class of Singular Systems with Actuator Saturation

Abstract

Robust control problem of singular system with actuator saturation is studied. Stability condition for nominal system with actuator saturation is derived based on Lyapunov theory. As nonlinear uncertainty widely exists in real systems, a compensator controller and parameter adaptive law are designed for a class of singular nonlinear systems, and the linear matrix inequality condition is derived for system stability. The results of this paper could be regarded as the extension of singular system theory with actuator saturation. At the end of this article, an example is given to show the correctness and effectiveness of the proposed method.

1 Introduction

Singular systems, also known as descriptor systems, implicit systems and differential algebraic systems, are widely used in the fields of electric power, economy, aviation and chemical industry systems. In recent years, many scholars have carried out research on the control problems of singular system [1, 2]. The robust H _∞ control problem for a class of singular systems was studied in [3]. First, the sufficient condition for solving the H _∞ control problem is given by using the state feedback and the output feedback control method. Then, based on two Hamilton-Jacobi inequalities and a weak coupling condition, the necessary condition of H _∞ control for a class of singular systems by output feedback is given. In [4], two adaptive robust control approaches are proposed for structural and non-structural uncertainty respectively, the first control method achieves asymptotical stability and robustness of the closed-loop singular system, the second approach aims at a more general case where the stability of the system is obtained while avoiding the influence of potential problems such as parametric drift caused by un-modeled dynamics. The robust dissipative control problem was researched in [5], firstly, the sufficient conditions for the strict dissipation of the system are given based on the Lyapunov stability theory, and a state feedback controller is designed to achieve the asymptotic stability of closed-loop systems.

Actuator saturation is a common physical phenomenon in practical systems. In recent years, the analysis and design problems of systems with actuator saturation have attracted the attention of many researchers [6, 7]. However, in the case of actuator saturation, little work has been done for singular systems, especially nonlinear singular systems. Different from [6], we give the existence condition of the stabilization controller based on the Lyapunov indirect method. In [7], the control design of a class of affine singular systems with actuator saturation is studied. State feedback stabilization controller, robust controller and adaptive controller are designed respectively. It should be pointed out that the theorem 4 in [7] cannot be established according to Schur complement lemma.

Adaptive robust control method has been applied to many uncertain systems [8, 9]. In [8], an adaptive robust control method is applied to nonlinear systems with parametric uncertainties and external disturbances, where the system disturbance has an upper bound which can be determined by a known function. In [9], adaptive variable structure control is applied to a nonlinear system with uncertain input-output linearization, in which the uncertainty bound is considered to be known and can be expressed as a product of a known function and a positive constant, and the objective of the adaptive design is to estimate the unknown constants within the system. In this paper, in order to enhance the robustness of the system and the practicality of control method, the system uncertainties are considered to be represented by the product of a known functions set and an unknown adaptive parameter.

In this paper, we study the stabilization and adaptive robust control problem for a class of singular systems with actuator saturation. The Lyapunov stability theory is used to derive the stablizable condition of the system. For the nonlinear uncertainties which exist widely in practical systems, an adaptive compensation controller is designed for matching nonlinear uncertainties, the LMI conditions and control parameter conditions for the system to be robust is derived. Finally, the simulation experiment is carried out for the singular system with disturbance, and the simulation results show the correctness and validity of the proposed method.

2 System Description

We consider the following singular system with nonlinear uncertainty:

$$ E\dot{x}\left( t \right) = Ax\left( t \right) + Bsat\left( u \right) + g\left( {x,p,t} \right) $$

(1)

where, $x \in R^{n}$ is state vector, $u \in R^{m}$ is control input vector, $g\left( {x,p,t} \right)$ is nonlinear uncertainty, $p \in P$ is unknown parameter vector, $P$ is the admissible set of the system. $E \in R^{n \times n}$ is singular matrix, i.e. $rank\;E = r < n$, matrix $A$ and $B$ are real matrices with appropriate dimension. $sat\left( u \right) =$ $\left[ {sat\left( {u_{1} } \right),sat\left( {u_{2} } \right), \cdots ,sat\left( {u_{m} } \right)} \right]^{\text{T}}$, $sat\left( \cdot \right)$ is nonlinear saturation function, defined as:

$$ \begin{aligned} sat\left( {u_{i} } \right) = \left\{ {\begin{array}{*{20}c} {s_{i} ,} & {u_{i} > s_{i} } \\ {u_{i} ,} & { - s_{i} \le u_{i} \le s_{i} ,\,,i = 1,2, \cdots ,m.} \\ { - s_{i} ,} & {u_{i} < - s_{i} } \\ \end{array} } \right. \hfill \\ \hfill \\ \end{aligned} $$

Definition 1

[1]

• (1) If there exist a complex number $s$ such that $\det \left( {sE - A} \right)\not \equiv 0$, then matrix pencil $\left( {E,A} \right)$ is called to be regular;

• (2) If $\deg \left( {\det \left( {sE - A} \right)} \right) = rank\left( E \right)$, then matrix pencil $\left( {E,A} \right)$ is called to be impulse-free;

• (3) If matrix pencil $\left( {E,A} \right)$ is regular, stable and impulse-free, then it is admissible.

Lemma 1

[10] Matrix pencil $\left( {E,A} \right)$ admissible, if and only if there exists matrix $X \in R^{n \times n}$ such that

$$ \begin{aligned} & E^{\text{T}} X = X^{\text{T}} E \ge 0 \\ & A^{\text{T}} X + X^{\text{T}} A < 0. \\ \end{aligned} $$

3 Adaptive Robust Control

The stabilization problem of singular system with actuator saturation can be described as follows:

For the nominal system of system (1):

$$ E\dot{x}\left( t \right) = A\,x\left( t \right) + B\,sat\left( u \right) $$

(2)

Finding a state feedback control law

$$ u\left( t \right) = Kx\left( t \right) $$

(3)

Such that the closed-loop system is asymptotic stable.

Lemma 2

[11] Let $\eta = u - sat\left( u \right)$, there exists a real constant $\varepsilon \in \left( {0,1} \right)$ such that:

$$ \eta^{\text{T}} \eta \le \varepsilon u^{\text{T}} u. $$

The adaptive robust control problem of system (1) can be described by designing the controller $u\left( t \right) = \alpha \left( {x,\theta } \right)$ and the parameter adaptive law $\dot{\hat{\theta }} = \beta \left( {x,\hat{\theta }} \right)$, such that the closed loop system achieves asymptotic stability under the nonlinear uncertainty $g\left( {x,t} \right)$. $g\left( {x,t} \right)$ is a time varying nonlinear perturbation with $g\left( {0,t} \right) = 0$ and satisfies the following Lipschitz condition:

$$ \left\| {g\left( {x_{1} } \right) - g\left( {x_{2} } \right)} \right\| \le \varsigma \left\| {M_{i} \left( {x_{1} - x_{2} } \right)} \right\| $$

(4)

In this article, the nonlinear uncertainty $g\left( {x,p,t} \right)$ is approximated by an RBF neural networks model

$$ \begin{aligned} & \hat{g}\left( {\hat{x},p,t} \right) = \xi^{\text{T}} \left( {\hat{x},t} \right)\hat{\theta }\left( p \right) \\ & \xi \left( {\hat{x},t} \right) = diag\left( {\xi_{1} ,\xi_{2} , \cdots ,\xi_{m} } \right) \\ & \hat{\theta } = \left[ {\hat{\theta }_{1} ,\hat{\theta }_{2} , \cdots ,\hat{\theta }_{m} } \right]^{\text{T}} \\ \end{aligned} $$

where, $\hat{\theta }\left( p \right)$ is unknown adaptive parameter vector, $\xi \left( {\hat{x},t} \right)$ is known Gaussian basis function.

It is assumed that there is an optimal weight matrix $\theta$ such that the approximation error is minimized, i.e.

$$ \theta \triangleq \,\arg \mathop {\hbox{min} }\limits_{{\hat{\theta }}} \left\| {g\left( {x,p,t} \right) - \hat{g}\left( {\hat{x},p,t} \right)} \right\| $$

and this optimal weight matrix is assumed to be piecewise constant, or slow time-varying, i.e. $\dot{\theta } = 0$.

It is shown in [9, 10] that, if $\hat{x}$ is restricted to a compact set $X \subset R^{n}$, for a large enough number hidden layer neurons in neural network, there always exist a constant $\theta$ such that any nonlinear function can be estimated accurately by an RBF networks model.

Theorem 1

For the singular system (1) with actuator saturation and nonlinear uncertainty, if there exists positive definite matrix $P$ such that the following conditions are satisfied:

$$ E^{\text{T}} P = P^{\text{T}} E $$

(5)

$$ P^{\text{T}} A + \frac{1}{2}P^{\text{T}} BB^{\text{T}} P < 0 $$

(6)

then the adaptive robust control problem of system (1) can be solved by the following control law $u\left( t \right)$ which is numerical solutions of the following equation

$$ au^{\text{T}} u + bu + c = 0 $$

(7)

and the adaptive law

$$ \dot{\hat{\theta }} = - \rho^{ - 1} \xi B^{\text{T}} Px $$

(8)

where, $a$,$c$,$\lambda$,$\rho$, are real constants, $b$ is real vector, $a = 0.5\varepsilon$, $b = x^{\text{T}} P^{\text{T}} B$, $c = x^{\text{T}} P^{\text{T}} B\xi^{\text{T}} \hat{\theta }$.

Proof

Using the Lipschitz condition (4), we can always achieve $u\left( t \right)$ from Eq. (7). Select the Lyapunov candidate function

$$ V = \frac{1}{2}x^{\text{T}} P^{\text{T}} Ex + \frac{1}{2}\tilde{\theta }^{\text{T}} \rho \tilde{\theta } $$

where $\tilde{\theta } = \theta - \hat{\theta }$, the derivative of $V$ is

$$ \begin{aligned} & \dot{V} = x^{\text{T}} P^{\text{T}} Ax - x^{\text{T}} P^{\text{T}} B\eta + x^{\text{T}} P^{\text{T}} Bu + x^{\text{T}} P^{\text{T}} B\xi^{\text{T}} \theta + \tilde{\theta }^{\text{T}} \rho \dot{\tilde{\theta }} \\ & \le x^{\text{T}} P^{\text{T}} Ax + \frac{1}{2}x^{\text{T}} P^{\text{T}} BB^{\text{T}} Px + \frac{1}{2}\eta^{\text{T}} \eta + x^{\text{T}} P^{\text{T}} Bu + x^{\text{T}} P^{\text{T}} B\xi^{\text{T}} \theta + \tilde{\theta }^{\text{T}} \rho \dot{\tilde{\theta }} \\ \end{aligned} $$

Using lemma 2 and Eq. (7), we obtain

$$ \dot{V} \le x^{\text{T}} P^{\text{T}} Ax + \frac{1}{2}x^{\text{T}} P^{\text{T}} BB^{\text{T}} Px + x^{\text{T}} P^{\text{T}} B\xi^{\text{T}} \tilde{\theta } + \tilde{\theta }^{\text{T}} \rho \dot{\tilde{\theta }} $$

Using the adaptive law (8), we obtain

$$ \dot{V} \le x^{\text{T}} P^{\text{T}} Ax + \frac{1}{2}x^{\text{T}} P^{\text{T}} BB^{\text{T}} Px $$

Therefore, the asymptotic stability can be achieved under control law $u\left( t \right)$.

Remark

In order to obtain matrix $P$, we need the following transformation:

$$ \bar{P} = U^{{ - {\text{T}}}} PM = \left[ {\begin{array}{*{20}c} {\bar{P}_{11} } & {\bar{P}_{12} } \\ {\bar{P}_{21} } & {\bar{P}_{22} } \\ \end{array} } \right],\quad \bar{E} = UEM = \left[ {\begin{array}{*{20}c} {I_{r} } & {} \\ {} & 0 \\ \end{array} } \right] $$

where, $U$ and $M$ are invertible matrices.

From Eq. (5), we obtain

$$ \begin{aligned} & \bar{E}^{\text{T}} \bar{P}{ = }M^{\text{T}} E^{\text{T}} U^{\text{T}} U^{{ - {\text{T}}}} PM = M^{\text{T}} P^{\text{T}} U^{ - 1} UEM = \bar{P}^{\text{T}} \bar{E} \\ & \bar{E}^{\text{T}} \bar{P} = \bar{P}^{\text{T}} \bar{E} \ge 0 \Rightarrow \bar{P}_{11} = \bar{P}_{ 1 1}^{\text{T}} \ge 0,\bar{P}_{12} = 0 \Rightarrow \bar{P} = \left[ {\begin{array}{*{20}c} {\bar{P}_{11} } & 0 \\ {\bar{P}_{21} } & {\bar{P}_{22} } \\ \end{array} } \right] \\ & P = U^{\text{T}} \left[ {\begin{array}{*{20}c} {\bar{P}_{11} } & {} \\ {} & 0 \\ \end{array} } \right]UU^{ - 1} \left[ {\begin{array}{*{20}c} {I_{r} } & {} \\ {} & 0 \\ \end{array} } \right]M^{ - 1} + U^{\text{T}} \left[ {\begin{array}{*{20}c} 0 \\ {I_{n - r} } \\ \end{array} } \right]Q^{ - 1} Q\left[ {\begin{array}{*{20}c} {\bar{P}_{21} } & {\bar{P}_{22} } \\ \end{array} } \right]M^{ - 1} \\ & = ZE + LY \\ \end{aligned} $$

where, $Z = U^{\text{T}} \left[ {\begin{array}{*{20}c} {\bar{P}_{11} } & {} \\ {} & 0 \\ \end{array} } \right]U$, $Y = N\left[ {\begin{array}{*{20}c} {\bar{P}_{21} } & {\bar{P}_{22} } \\ \end{array} } \right]V^{ - 1}$. Matrix $L$ satisfies $E^{\text{T}} L = 0$, and $L = U^{\text{T}} \left[ {\begin{array}{*{20}c} 0 \\ {I_{r} } \\ \end{array} } \right]Q^{ - 1}$. To obtain matrix $P$, we just need matrix $Z$ and matrix $Y$.

4 Simulation Example

In this section, we propose the adaptive robust controller for nonlinear singular systems with actuator saturation based the conclusion in Sect. 3.

To validate the effectiveness of this paper, in this section, we give a simulation example, where the parameters are:

$$ E = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 0 \\ \end{array} } \right],\quad A = \left[ {\begin{array}{*{20}c} { - 3} & 2 \\ 1 & { - 3} \\ \end{array} } \right],\quad B = \left[ {\begin{array}{*{20}c} {0.5} & 0 \\ 0 & {0.5} \\ \end{array} } \right], $$

Using the LMI toolbox in Matlab, the following matrix can be obtained:

$$ \begin{aligned} & Z = \left[ {\begin{array}{*{20}c} { 5. 8 5 5 6} & { 1 6. 7 6 5 6} \\ { 1 6. 7 6 5 6} & 0\\ \end{array} } \right],\quad P{ = }\left[ {\begin{array}{*{20}c} { 5. 8 5 5 6} & 0\\ { - 1.1940} & { 1 3. 9 6 6 6} \\ \end{array} } \right], \\ & Y{ = }\left[ {\begin{array}{*{20}c} { - 17.9596} & { 1 3. 9 6 6 6} \\ \end{array} } \right] \\ \end{aligned} $$

The initial state is $x\left( 0 \right) = \left[ {\begin{array}{*{20}c} { - 1} & 0 \\ \end{array} } \right]^{\text{T}}$. Nonlinear uncertain function is $g\left( t \right) = \sin \left( t \right)$.

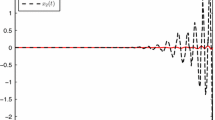
The curve of uncertainty $g$ and its estimation $\hat{g}$ are shown in Fig. 1, the response of the state $x_{1}$ is shown in Fig. 2, and the control signal curve is shown in Fig. 3.

Fig. 1

Uncertainty $g$ and its estimation $\hat{g}$

Fig. 2

Response of the state $x_{1}$

Fig. 3

Control input curve $sat\left( u \right)$

It can be observed from Fig. 1 that the output of neural network converges to the uncertainty, therefore, in Fig. 2 that the system state converges to the origin quickly under the effect of nonlinear uncertainty. Simulation results show that the system controller works very well in attenuating external uncertainty.

5 Conclusions

In this article, a class of singular systems with nonlinear uncertainties and actuator saturation is studied, an adaptive robust controller is designed for the nonlinear uncertainties of the system. The asymptotic stability of the closed-loop system is proved based on the Lyapunov stability theory, and the correctness of the method is proved by the simulation experiment. The method of this paper enriches the adaptive robust control of singular systems, which can be regarded as a supplement and perfection under the condition of actuator saturation.