Keywords

1 Introduction

In recent years, the chaos theory is deeply studied in various fields. Due to the extreme sensitivity of chaotic systems to initial parameters, they can be used for weak signal detection and extraction. In the chaotic systems known, Duffing oscillator is more suitable for detecting sinusoidal signal, which is the current research hot spot in many fields, such as exploration seismology, unmanned plane inspection, etc. [1,2,3,4,5,6]. However, most of the materials are limited to pure numerical simulation, and the Duffing circuit has not been studied in depth.

There are fewer simulation Duffing circuits, but they are only adequate for very low frequencies. Such as reference [7]. Simulation results showed that with the increase of ω, it is more and more inconsistent with the theoretical analysis. The signal frequency is limited to about 1 Hz.

In order to solve this problem, we establish a new Duffing equation suitable for high frequency by a time-scale transformation, based on it, we design a new Duffing circuit for low to high frequency signals, and effectively solve the instantaneous saturation problem of the circuit. We also introduce the operational block diagram and design process for the important circuit unit. At last we study its initial sensitivity at high frequency ω = 106 rad/s (159,155 Hz) by Multisim software. Simulation results show that the circuit is very sensitive to weak sinusoidal signals. It provides the basis for the practical application of Duffing oscillator.

2 A New Method to Establish Duffing Circuit

As we know, the commonly used Duffing equation to design circuit is

$$ \left\{ {\begin{array}{*{20}l} {\frac{{dy_{1} }}{dt} = y_{2} } \hfill \\ {\frac{{dy_{2} }}{dt} = r\cos \,\omega t - ky_{2} + y_{1}^{3} - y_{1}^{5} } \hfill \\ \end{array} } \right. $$
(1)

where k is the damping ratio, generally let k = 0.5 [1], y 31 −y 51 is the nonlinear restoring force, rcosωt is the forced periodic term, ω is the angular speed. If k is fixed, With the increase of r, the system experiences the homoclinic orbit, period doubling bifurcation, chaos, the chaotic critical state (chaos, but on the verge of changing to the large-scale periodic state), until r is greater than a threshold r d, the system enters the large-scale periodic state [2]. By observing the complete different phase trajectories between the chaotic state and the large-scale periodic state, we can identify the weak sinusoidal signals [4, 5].

According to the minikev method, only in the case of low frequency, stable invariant manifolds and unstable invariant manifolds in the Poincare map of the Eq. (1) will intersect, then homoclinic intersections appear [1]. So the Duffing system may enter the chaos. But if the frequency is higher, the system can not enter the chaotic state. To solve above problem, we make a time scale transformation for (1), and obtain a new Duffing system as

$$ \left\{ {\begin{array}{*{20}l} {\frac{{dy_{1} }}{dt} = \omega y_{2} } \hfill \\ {\frac{{dy_{2} }}{dt} = \omega (r\,\cos (\omega t) - 0.5y_{2} + y_{1}^{3} - y_{1}^{5} )} \hfill \\ \end{array} } \right. $$
(2)

In the new phase space, the phase velocities y 1 and y 2 increase ω times. As long as we change the value of the ω in (2), it can be adapted to different frequencies.

Equation (2) is a new Dufffing system to be used in this paper. According to it, we will design a new type of Duffing circuit. For convenience, we rewrite (2) in integral form. let \( r = \sqrt 2 f \), where f is the root mean square (RMS) value, then use \( \sqrt 2 f\,\sin \omega t \) to replace the forced periodic term in (2), finally integrate it on both sides and get [2].

$$ \left\{ {\begin{array}{*{20}l} {y_{1} = \int {\omega y_{2} dt + C_{1} } } \hfill \\ {y_{2} = \int {\omega (\sqrt 2 f\, \sin\;\omega t - 0.5y_{2} + y_{1}^{3} - y_{1}^{5} )} dt + C_{2} } \hfill \\ \end{array} } \right. $$
(3)

where C 1 and C 2 are integral constants. If y 1(t 0) = y 1(0) = 0, y 2(t 0) = y 2(0) = 0, C 1 and C 2 are both zero. Before integration, y 2 and \( (\sqrt 2 f\,\sin \omega t - 0.5y_{2} + y_{1}^{3} - y_{1}^{5} ) \) are multiply by ω at first respectively. When ω is large, such as ω is 106 rad/s, the value of the integral item will be very large. In the design of the circuit, even we can achieve a 106 amplification by a high magnification amplifier, but because the amplifier’s supply voltage is generally ±15 V, the circuit will be instantaneous saturation. To solve this problem, we do integral calculation at first, and then multiply by ω, so (3) becomes

$$ \left\{ {\begin{array}{*{20}l} {y_{1} = \omega \int_{0}^{t} {y_{2} dt} } \hfill \\ {y_{2} = \omega \int_{0}^{t} { (\sqrt 2 f\, \sin\omega t - 0.5y_{2} + y_{1}^{3} - y_{1}^{5} )dt} } \hfill \\ \end{array} } \right. $$
(4)

If we let the circuit do the integral at first and then multiply by ω, the corresponding voltages will be reduced ω times, and then magnified ω times. Thus the circuit can successfully avoid the momentary saturation. The circuit established according to (4) is a new type of Duffing circuit, which can be achieved by devices such as op amps.

3 Detailed Design of the Duffing Circuit

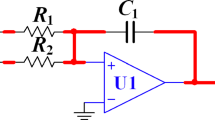
We draw an overall operational block diagram which can show the function of each unit circuits as shown in Fig. 1. For convenience, the labels of elements in Figures in this paper are consistent. To illustrate the proportional coefficient K of the inverting amplifier 1# and 2# in Fig. 1, an integrator is first introduced as shown in Fig. 2. Its input and output voltages meet the following relationship

Fig. 1
figure 1

Operational block diagram

Full size image
Fig. 2
figure 2

Analog integrator

Full size image
$$ U_{0} = - \frac{1}{RC}\int_{0}^{t} {U_{i} dt} $$
(5)

The output voltage U o is proportional to the integral of the input voltage U i with a proportion coefficient of −1/(RC). Therefore, R 1 C 1 and R 15 C 2 in Fig. 1 are introduced by taking into account of this proportional coefficient. As long as the R 1 C 1 and R 15 C 2 are appropriately adjusted, the circuit can achieve signal detection from low to high frequency. For example, we let ω = 106 rad/s (f = 159,155 Hz), the magnification of the inverting amplifier 1# K 1 = R 1 C 1 ω. The closed-loop magnification of single-stage op amp is generally less than 100. Here let K 1 = 10, then

$$ R_{1} C_{1} = k_{1} /\omega = 1/10,00,000 = 10^{ - 5} $$
(6)

Let K 2 = 1, where K 2 is the amplification of the inverting amplifier 2#, we obtain

$$ R_{15} C_{2} = k_{2} /\omega = 1/10,00,000 = 10^{ - 6} $$
(7)

So we can select the appropriate R 15 and C 2 according to (7). Unit circuits include the summing integrator, inverting integrator, inverting adder, inverting amplifier 1# and 2# and multipliers. Here we introduce the design of the inverting integrator in detail. The summing integrator design is similar to the inverting integrator. Others are conventional design [8]. The integrator is shown in Fig. 3, and its integral relationship is expressed as

Fig. 3
figure 3

Inverting integrator

Full size image
$$ U_{4} = - \int_{0}^{t} {U_{2} dt} $$
(8)

From (7), we know the time constant τ f = R 15 C 2 = 10−6 s, τ f is determined by the closed-loop magnification K 2 of the inverting amplifier 2#. If the maximum output of the amplifier is V om, and its input is a sinusoidal signal, according to the design principle of the integrator, R 15 C 2 must meet the relationship V om ≥ r/R 15 C 2 ω.

For the Duffing circuit, r is generally less than 2, the op amp DC power supply voltage is generally ±15 V, V om is usually about 70% of the supply voltage, so it is generally ±10 V, thus R 15 C 2 ≥ 1.9 × 10−7. The value of R 15 C 2 is 10−6, which is satisfied the above requirements. Here choose R 15 = 1.0 kΩ, C 2 = 1.0 nF. In conventional design, R 16 is 10 times of R 15, Here let R 16 = 10 kΩ.

In Fig. 4, ω f is the intersection of the ideal integrator amplitude-frequency characteristic and the horizontal axis, Its value ω f = 1/R 15 C 2 = 106 rad/s.

Fig. 4
figure 4

Amplitude frequency characteristics of the integrator. 1—Open loop amplitude frequency characteristic of operational amplifiers. 2—Amplitude frequency characteristics of ideal integrator

Full size image

ω of is the frequency corresponding to the intersection of the ideal integrator amplitude-frequency characteristic and the open-loop amplitude-frequency characteristic of the op amp, and ω 0f = ω f/A 0.

(ω 0f ~ ω c) is the normal working section of the integrator. Here let the open-loop voltage magnification of the op amp A 0 = 105, then

$$ \omega_{0f} = \frac{{\omega_{f} }}{{A_{0} }} = \frac{{10^{6} }}{{10^{5} }} = 10 \;{\text{rad/s}} $$
(9)

Since the cutoff frequency ω 0 > ω of = 10 rad/s, ω 0 is at least 10 rad/s. Therefore, the unity gain bandwidth ω c = A 0 ω 0 = 106 rad/s. ω c is at least 106 rad/s, namely ω c > 106 rad/s.

Duffing circuit often works in the large signal state. The key specification for its instantaneous response is the slew rate S r. When the input signal is a sine wave, the maximum slope of the waveform should be less than the slew rate of the op amp.

If input voltage u i = rcosωt, the collector voltage of the amplifier output stage is

$$ u_{o} = - \frac{1}{{R_{15} C_{2} }}\int_{0}^{t} {r\, \cos (\omega t )} dt = \frac{ - r}{{R_{15} C_{2} \omega }} \sin\,\omega t $$
(10)

The slope of u o is

$$\frac{{du_{0} }}{dt} = \frac{ - r}{{R_{15} C_{2} }} \cos\,\omega t $$
(11)

The maximum slope of u o is r/R 15 C 2. Since r is less than 2, so the maximum slew rate is S rmax > r/R 15 C 2 = 2×106 V/s. Therefore, the selected op amp should have a slew rate greater than 2 × 106 V/s. Here we emphasize that the slew rate design is very important, but easy to be ignored. If the slew rate is not appropriate, the circuit can not work properly at all. In summary, the selected op amp will be that its cutoff frequency ω 0 is greater than 10 rad/s, unity gain bandwidth ω c is greater than 106 rad/s, open-loop voltage amplification A 0 is 105, slew rate is greater than 2 × 106 V/s. Here we choose 3554 AM as the op amp.

4 Circuit Simulation

A new Duffing circuit is as shown in Fig. 5. Its simulations are done by Multisim software [9]. In Fig. 5, V 1 is a sinusoidal voltage source, multipliers are A 1–A 4, and other elements are selected from the Multisim device library. The output voltage U 2 of the 3554AM2 corresponds to y 2, and the output voltage U 5 of the 3554AM5 corresponds to y 1 in Eq. (4). Timing diagrams and phase plane orbit diagrams can be observed by connecting the B-channel of oscilloscope XSC1 to voltage U 5 and A-channel to voltage U 2. If the input signal source V 1 is

Fig. 5
figure 5

New Duffing chaotic circuit

Full size image
$$ u = r\,\sin \omega t = \sqrt 2 f\,\sin \omega t $$
(12)

where r changes between 0 and 1 V, and correspondingly EMS f varies between 0 and 0.707 V, ω is 106 rad/s. Since the power supply in Multisim appears as EMS values, it is convenient to change f for voltage adjustment. In addition, the oscilloscope scale is that each division represents 500 mV in phase plane orbit diagrams.

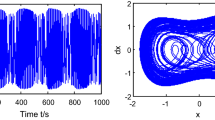
When f is from 0 to 1, from simulation results we know the system experiences the periodic oscillation, homoclinic orbit, chaos, and finally large-scale periodic state. In particular, when f = 0.52556171 V, the system appears as a critical chaotic state, as shown in Fig. 6a. If the power supply EMS value increases 0.00000001 V, namely f = 0.52556172 V, the circuit is from the chaotic state to large-scale periodic state, as shown in Fig. 6b.

Fig. 6
figure 6

Phase plane orbit diagrams and timing diagrams of U 5

Full size image

Simulation results show that this new Duffing circuit has the extreme sensitivity to the initial condition. Thus it has the prerequisite to detect weak sinusoidal signals at high frequency.

5 Summary

Since the common Duffing circuit is limited to low frequency signals, this paper proposes a new type of Duffing detection circuit which effectively avoids instantaneous saturation at high-frequency. If the op amp performance is good enough, it can realize the wide frequency detection from low frequency to high frequency by adjusting the parameters of several elements.

It also gives a circuit operational block diagram, and then according to the block diagram, gives the detailed design of the main unit circuit.

We make simulations on the new Duffing chaotic circuit by the Multisim software. Phase plane orbit diagrams and timing diagrams are observed by the oscilloscope. Simulation results prove that the circuit is a chaotic system and has the extreme sensitivity to the initial condition. Therefore it has the prerequisite to detect weak sinusoidal signals at high frequency.