Keywords

1 Introduction

Most of today’s defence operations such as rescue in dense forest, landing of aircrafts on ships, tracking of unidentified radio source depend on three main functions, navigation, tracking and Guiding, and it is unimaginable to find a system that does not have any relation with these functions. These systems require to determine the two- or three-dimensional position information of an object of interest, and they use GPS receivers for this purpose. GPS is the constellation of space bodies called satellites which revolve round the earth and provide position information based on range measurements. With a sufficient number of range measurements, GPS can provide position estimates to high degree accuracy [1]. The accuracy in turn is the function of type of equipment, geographic area, uncertainty in measurements, navigation algorithm, etc. In practice, the measurement uncertainty can never reach zero even though the system noise parameters and biases are modelled effectively and hence need a high accuracy navigation algorithm that makes out an optimal estimate from these uncertain measurements.

The various algorithms used for GPS receiver position estimate include least squares (LS), weighted least squares (WLS), evolutionary optimizers, Kalman filter (KF). The task of tracking and guiding involves estimation of objects’ future course, and this could be only possible when the system dynamics are modelled into the estimator. Out of the available navigation algorithms, the only filter that makes use of the dynamics in estimation is Kalman filter [2]. In addition, KF also provides the uncertainty in its estimation whose performance varies with parameters such as process noise matrix, measurement noise matrix, geometry matrix. So this paper concentrates in improving KFE accuracy with a new geometry matrix that replaces the conventional matrix in Kalman filter’s covariance update equation. The modelling of KF as GPS receiver position estimator and the details about new designed geometry matrix lead to the development of MVKF are discussed in subsequent sections.

2 Modified Variance Kalman Filter for GPS Applications

As depicted in Fig. 1, GPS uses time of arrival (TOA) measurements observed between satellite, Sat i , and GPS receiver, R X , to compute the receiver position. GPS \({\text{TOA}}_{{{\text{Sat}}_{i} ,\,{R_x}}}\) measurement is the travel time of a radio signal between the receiver, R X , and ith satellite, Sat i , and with known signal velocity, it provides the range information. The range equation formulated in Eq. 1 is nonlinear [3] and requires minimum four such equations to be solved to get precise GPS position.

Fig. 1
figure 1

Positioning with GPS TOA measurements

Full size image

Hence, extended Kalman filter estimator (EKFE) or Kalman filter estimator (KFE) with linearized measurement equations is used to estimate the unknown receiver position. The first-order approximated linear form Taylor’s series [4] of Eq. 1, computed at \(\hat{R}_{X}\), is given in Eq. 2 which is used in framing the geometry matrix, ψ in KFE.

$$\begin{aligned} {\text{TOA}}_{{{\text{Sat}}_i,R_x}} &= f\left( {{\text{Sat}}_i,R_x} \right) = \sqrt {(x_{{{\text{Sat}}_i}} -x_{R_x} )^{2} + (y_{{{\text{Sat}}_i}} - y_{R_x} )^{2} + (z_{{{\text{Sat}}_i}} - z_{R_x} )^{2} } \\ & \quad \quad i = 1,2\ldots, {\text{no}}. \, {\text{of}}. \, {\text{satellites}} \\ \end{aligned}$$
(1)
$$f({\text{Sat}},R_x) \cong f({\text{Sat}},\hat{R}_x) + f^{\prime } ({\text{Sat}},\hat{R}_x)(R_x- \hat{R}_x)$$
(2)

Here, \({\text{TOA}}_{{{\text{Sat}}_{i}} ,\,{{\text{R}_x}}}\) is the time of arrival between ith satellite, Sat i and GPS receiver, R x , \({\mathbf{Sat}} = \left( {x_{{{\text{Sat}}_{i}}} ,y_{{{\text{Sat}}_{i}}} , z_{{{\text{Sat}}_{i}}}} \right)\) is the three-dimensional position coordinates of ith satellite, \({\mathbf{R}}_{\mathbf{x}} = \left( {x_{R_x} ,y_{R_x} ,z_{R_x} } \right),{\hat{\mathbf{R}}}_{x} = \left( {\hat{x}_{R_x} ,\hat{y}_{R_x} ,\hat{z}_{R_x} } \right)\), is the three-dimensional position coordinates of receiver, and its estimate, respectively, and f′ represents the first-order derivative of nonlinear function, f(Sat, R x ) w.r.t, \(\hat{R}_{X}\).

The other form Eq. 2 can be represented is

$$f(\text{Sat},R_x)- f(\text{Sat},\hat{R}_x) \cong f^{\prime} (\text{Sat},\hat{R}_x)(R_x- \hat{R}_x){ \Rightarrow }\delta \text{TOA}_{{\text{Sat},R_x}} \cong \frac{{\partial f(\text{Sat},R_x)}}{{\partial \hat{R}_x}}\delta R_x \Rightarrow \delta {\text{TOA}}_{\text{Sat}},R_x \cong \psi ({\text{Sat}},\hat{R}_x)\delta R_x$$

where

$$\frac{{\partial f(\text{Sat},R_x)}}{{\partial \hat{R}_x}} = \frac{{\left( {\hat{X}_{R_x} - X_{\text{Sat}} } \right)}}{{\text{TOA}_{{\text{Sat},\hat{R}_{x} }} }}\delta \hat{X}_{R_x} + \frac{{\left( {\hat{y}_{R_x} - Y_{\text{Sat}} } \right)}}{{\text{TOA}_{{\text{Sat},\hat{R}_{x} }} }}\delta \hat{Y}_{R_x} + \frac{{\left( {\hat{Z}_{R_x} - Z_{\text{Sat}} } \right)}}{{\text{TOA}_{{\text{Sat},\hat{R}_{x} }} }}\delta \hat{Z}_{R_x}$$
(3)

Here, \(\delta {\text{TOA}}_{{{\text{Sat}},\,{\text{R}}_x}}\) is the error or change in range measurements, δR x is the error or change in receiver position and the term \(\partial f\left( {\text{Sat},\hat{R}_x} \right)/\partial \hat{R}_x\) represents geometry matrix, ψ or Jacobian matrix, J, given in Eq. 3.

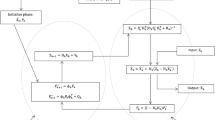
As mentioned previously in order to provide the position estimates and the uncertainty in estimation, KFE uses the geometry matrix, ψ in two stages [5], time updation and measurement updation which are formulated as below.

  • Time Updation:

$$R_{{x}_{t/t - 1}} = \varPhi R_{{x}_{t - 1/t - 1}} + P_{R_x}$$
(4)
$$C_{t/t - 1} = \varPhi R_{{x}_{t/t - 1}} \varPhi^{T} + \xi$$
(5)
$$G_{\text{K}} = C_{t/t - 1} \psi_{t/t - 1}^{T} \left( {\psi_{t/t - 1} C_{t/t - 1} \psi_{t/t - 1}^{T} + \beta } \right)^{- 1}$$
(6)

  • Measurement Updation:

$$R_{{x}_{t/t}} = R_{{x}_{t/t - 1}} + G_{\text{K}} (\text{TOA}_{t} - \psi_{t/t - 1} R_{{x}_{t/t - 1}} )$$
(7)
$$C_{t/t} = \left( {I- G_{\text{K}} \psi_{{{t \mathord{\left/ {\vphantom {t {t- 1}}} \right. \kern-0pt} {t- 1}}}} } \right)C_{{{t \mathord{\left/ {\vphantom {t {t- 1}}} \right. \kern-0pt} {t - 1}}}}$$
(8)

where \(R_{{x}_{t /t - 1}}\) is the receiver position estimate at time (t) prior collection of measurements, \(R_{{x}_{t/t}}\) is the estimate of receiver position at time (t) on post reception of measurements; TOA at time (t), C t/t-1 represents the uncertainty in the estimated receiver position at time (t) prior measurements, C t/t-1 represents the uncertainty in estimated receiver position at time (t) post the measurements, G K is the Kalman Gain, Φ represents receiver position state transition matrix, ψ is geometry matrix, I is the identity matrix, β the measurement error covariance matrix, P Rx and ξ are the process noise and its uncertainty, respectively.

It is observed from Eq. 3 that the geometry matrix, ψ is the resultant of first-order approximation from Taylor’s series and as defined in [6] a nonlinear function like f(Sat, R x ) is modifiable if there exist a linear structure which is the function of the predicted state, \(\hat{R}_x\) and the actual measurement, \({\text{TOA}}_{{{\text{Sat}},\,{R_x}}}\), i.e. if f(Sat, R x ) is modifiable than Eq. 3 can be rewritten as Eq. 9.

$$\delta {\text{TOA}}_{{\text{Sat},R_x}} = \varGamma \left( {\text{TOA}}_{{\text{Sat}},R_x} ,\hat{R}_x \right) \times \delta R_x$$
(9)

In practice, the range measurements, TOA, are noisy, and hence, \({\text{TOA}}_{{{\text{Sat}},R_x}}^{*}\) is used in Eq. 9 instead of \({\text{TOA}}_{{{\text{Sat}},\,{R_x}}}\). The developed MVKF makes use of the new observation matrix, Γ instead of ψ in Eq. 8, while retaining the other KFE equations as same [7]. Kalman gain, G K in Eq. 6, is the function of ψ, C t/t − 1 and β, which decides the amount of weight to be imposed on current measurements while updating the receiver position and hence making this equation the function of current measurements, \({\text{TOA}}_{{\text{Sat}},R_x}^{*}\) results in poor performance [6]. This is the reason the new observation matrix Γ is used in Eq. 8, and the resultant new updated covariance matrix for MVKE is given in Eq. 10

$$C_{t/t - 1} = \left( {I - G_{\text{K}} \varGamma_{t/t - 1} } \right)C_{t/t - 1}$$
(10)

3 Results and Discussion

The GPS receiver located at AUCE, Visakhapatnam, is used for the collection of real-time data, which is used in the performance evaluation of KFE and the developed MVKF estimator. The three-dimensional position of the receiver is estimated over a period of 23 h 56 min (2872 epochs) with a randomly chosen initial position estimate of X: 785 m, Y: 746 m and Z: 3459 m. The data is collected at a sampling interval of 30 s, and the position error of epochs the estimator took to reach convergence (i.e. position error in three dimensions <100 m) is plotted in Figs. 2 and 3. The details pertaining to the convergence epochs are also given in Table 1. It is observed from the figures and Table 1 that the developed algorithm, MVKF, converges at faster rate compared to conventional KFE.

Fig. 2
figure 2

Position error versus epochs. a Position error in X-coordinate with KFE and MVKF for AUCE, Visakhapatnam GPS receiver. b Position error in Y-coordinate with KFE and MVKF for AUCE, Visakhapatnam GPS receiver

Full size image
Fig. 3
figure 3

Position error in Z-Coordinate with KFE and MVKF for AUCE, Visakhapatnam GPS receiver

Full size image
Table 1 Estimator convergence performance
Full size table

Also the GPS statistical accuracy measures (SAM) for both the algorithms are calculated for the entire range of data and tabulated in Table 2. Various SAM [8] such as 1(σ) sigma error, circular error probability (CEP), spherical error probability (SEP), spherical accuracy standard (SAS), mean radial spherical error (MRSE), distance root mean square (DRMS) are used in the evaluation of the algorithms accuracy performance. Table 2 depicts the SAM of both the algorithms on AUCE and Visakhapatnam GPS receiver and is given below.

Table 2 SAM of KFE and the developed MVKF for AUCE, Visakhapatnam GPS receiver
Full size table

It is obvious from the accuracy measures that for AUCE, Visakhapatnam receiver the position estimated by the MVKF will be within 26.64 m from its true position with a probability of 0.99, where KFE estimates the position within 44.57 m. This shows the efficiency of developed algorithm over conventional KFE.

4 Conclusion

A new algorithm for the GPS receiver position estimation was developed based on predict and update concept of KFE. The geometry matrix designed out of first-order Taylor’s approximation of nonlinear measurement function is modified. The designed new geometry matrix is then used for modification of covariance update equation in KFE. The developed algorithm, MVKF performance, is evaluated with the collected real-time GPS data over a period of 23 h 56 min. The GPS receiver position located at AUCE, Visakhapatnam, is estimated with the collected data, and the algorithms’ performance is evaluated with various SAM. Results demonstrated that MVKF converges in less time (with an epoch difference of 40 for AUCE, Visakhapatnam) and has an accuracy difference of 2 m CEP when compared to conventional KFE. This also showed that the MVKF has faster convergence rate with high accuracy and is suitable for real-time defence applications such as navigation of ships, landing of CAT I and II aircrafts.