Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Rigorous results on homogenization are very important for today’s theoretical and applied mechanics. This is especially true for the numerical investigation of very complex systems, as even with today’s computational tools they may require a long computation time, and thus the a priori reliability of the results is of course desirable. The investigation of metamaterials (see [1] for a review of recent results) is among the topical research directions in which one often deals with very expensive numerical simulations, as the implementation of the desired (often exotic) properties at the macro-scale are usually realized by means of a very complex microstructure [2, 3]. The theory of microstructured/micromorphic continua is by now well developed, with several sound and interesting results (see e.g. [4, 5] as general references on Cosserat continua, [6,7,8] for related results and [9,10,11,12,13,14,15,16] for different kinds of applications of microstructured models). Still, it is necessary to develop suitable convergence arguments if one wants to solidly rely on the numerical simulations based on the solution of the simplified equations coming from the micromorphic/generalized continuum model used for the description of the metamaterial.

In the present chapter we focus on special micro-structured systems which can be described as discrete systems. In this case, the reliability of the homogenization has to be intended in two ways:

  1. 1.

    Real world micro-structured systems with suitably small characteristic lengths have to be well described by the homogenized continuum model;

  2. 2.

    The numerical simulation of the equations coming from the homogenized model (that are usually way simpler than the ones coming from the discrete model) has to converge in a suitable sense.

In principle, there is no reason to believe that the ordinary assumptions made for classical (Cauchy) continuum models are suitable for models describing objects that are so different from the phenomenology originally motivating them. Indeed, very often generalized continuum models are called for, and in particular higher gradient theories (see e.g. [17,18,19,20,21,22]) are being successfully employed in a number of cases for the homogenization of systems with complex geometry at the micro-scale [23,24,25,26,27]. In the present contribution we address this kind of question for Euler’s beam model (also known as Elastica), which is the elementary constituent for a large class of complex fibrous systems, including the promising case of pantographic sheets (see [28,29,30,31] for theoretical and numerical results and [32] for experimental ones in this direction). Specifically, we want to provide a rigorous justification for the discrete approximation by Heinrich Hencky (1885–1951) [33] of Euler’s beam model in large deformation, which is becoming increasingly topical in today’s research in structural and computational mechanics [34,35,36] and metamaterials [37]. In particular, we address here the ideal case in which the beam is perfectly inextensible, while future investigation will be devoted to the more general extensible case.

2 Convergence of Measure Functionals

Before setting the mechanical problem we are interested in, we need to recall some (well known) mathematical tools for describing the placement and the energy of the discrete beam model and define a suitable convergence for the sequence of the discrete energy functionals.

Let \((C[0,1])^{d}\) be the space of vector valued continuous functions on [0, 1] endowed with the uniform norm \(\Vert \varphi \Vert _{\infty }:=\sup \{ \Vert \varphi (t)\Vert : t\in [0,1]\}\) and \(({\mathscr {M}}[0,1])^{d}\) the set of vector valued bounded measures on [0, 1] endowed with the norm

$$\begin{aligned} \Vert \mu \Vert _{{\mathscr {M}}} :=\sup \{\langle \mu , \varphi \rangle : \varphi \in (C[0,1])^{d}, \Vert \varphi \Vert _{\infty }=1 \} \end{aligned}$$

where \(\langle ., .\rangle \) stands for the duality bracket between \(({\mathscr {M}}[0,1])^{d}\) and \((C[0,1])^{d}\). Recall that if a sequence of vector valued bounded measures \((\mu _n)\) satisfies \( \sup _n\Vert \mu _n\Vert _{{\mathscr {M}}} <+\infty \) then there exists a vector valued bounded measure \(\mu \) and a subsequence \((\mu _{n_k})\) which converges to \(\mu \) with respect to the weak\(^{*}-\)topology of \(({\mathscr {M}}([0,1])^{d}\) i.e.

$$ \lim _{k\rightarrow \infty }\langle \mu _{n_k} ,\varphi \rangle =\langle \mu ,\varphi \rangle $$

for every \(\varphi \in (C([0,1])^{d}\).

Let \((F_n)\) and F be functionals on \(({\mathscr {M}}[0,1])^{d}\) with values in \(\mathbb {R}\cup \{+\infty \}\). We say that \(F_n\) \(\varGamma -\) converges to F if the following holds [38]:

  1. i.

    Upper bound inequality. For every \(\mu \in ({\mathscr {M}}([0,1])^{d}\), there exists a sequence \((\mu _n)\) in \(({\mathscr {M}}[0,1])^{d}\) weak\(^{*}-\) converging to \(\mu \) for which

    $$ \limsup _{n\rightarrow \infty }F_n(\mu _n)\le F(\mu ). $$
  2. ii.

    Lower bound inequality. For every \(\mu \in ({\mathscr {M}}[0,1])^{d}\) and every sequence \((\mu _n)\) in \(({\mathscr {M}}[0,1])^{d})\) weak\(^{*}-\)converging to \(\mu \),

    $$ \liminf _{n\rightarrow \infty } F_n(\mu _n)\ge F(\mu ). $$

Such a \(\varGamma \)-convergence result is efficient when the following property of the sequence \((F_n)\) holds:

  1. iii.

    Relative compactness. For every sequence \((\mu _n)\) in \(({\mathscr {M}}[0,1])^{d}\)

    $$ \sup _{n}F_n(\mu _n)<+\infty \quad \Longrightarrow \quad \sup _n\Vert \mu _n\Vert _{{\mathscr {M}}}<+\infty . $$

Informally speaking, relative compactness ensures that controlling the deformation energy is enough to control, with the help of boundary conditions, the norm of the measure employed for the description of the current configuration of the discrete model.

3 Micro-Model for Non-Linear Beams

3.1 Discrete Configurations and Operators

Let \(\delta _t\) denote the Dirac measure at the point \(t\in [0,1]\). The reference configuration of the discrete micro-system is constituted by \(n+1\) nodes placed at the points \(\frac{i}{n}\), \(i=0, \dots , n\). Therefore it can be identified with a measure concentrated at the points \({\scriptstyle {\frac{i}{n}}}\) where \(i=0, 1, ... ,n\), more precisely with the positive Radon measure on [0, 1]

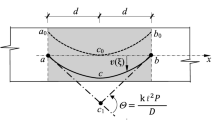
$$\begin{aligned} \overline{\nu }_n:={\frac{1}{n}}\sum _{i=0}^{n}\delta _{\frac{i}{n}} \end{aligned}$$
(1)

We assume that the reference (unstressed) configuration of the beam is straight, has unitary length and lays parallel to \(\mathrm{e}_1\), i.e. the first vector of the canonical base of \(\mathbb {R}^{d}\). The current configuration of the beam can be described by a vector bounded measure \(\mu \) on [0, 1] of the form \( \mu (dt):= u(t) \overline{\nu }_n (dt) \) where the placement function \(u :[0,1]\rightarrow \mathbf {R}^{d}\) is defined \(\overline{\nu }_n\)-almost everywhere i.e. at the points \({\scriptstyle {\frac{i}{n}}}\) where \(i=0,1, \dots ,n \) (see Fig. 1 for a graphical representation of the discrete model).

Fig. 1
figure 1

Graphical representation of Hencky discrete model consisting of inextensible bars and rotational springs. In the graph \(\theta _i:=\theta _n(u)({\scriptstyle {\frac{i}{n}}}\))

Full size image

In what follows, we will use the following notations:

$$\begin{aligned} \nu _n^{+}:={\frac{1}{n}}\sum _{i=0}^{n-1}\delta _{\scriptstyle {\frac{i}{n}}}, \qquad \nu _n^{-}:={\frac{1}{n}}\sum _{i=1}^{n}\delta _{\scriptstyle {\frac{i}{n}}}, \qquad \nu _n:={\frac{1}{n}}\sum _{i=1}^{n-1}\delta _{\scriptstyle {\frac{i}{n}}}, \end{aligned}$$
(2)
$$\begin{aligned} D_n^{+}u(t):=n\big ( u(t+{\scriptstyle {\frac{1}{n}}})-u(t)\big ), \qquad D_n^{-}u(t):=n\big ( u(t)-u(t-{\scriptstyle {\frac{1}{n}}})\big ), \end{aligned}$$
(3)
$$\begin{aligned} D^2_n u:=n(D_n^{+}u-D_n^{-}u). \end{aligned}$$
(4)

Note that, if u is a placement function, \(D_n^{+}u\) is defined \(\nu _n^{+}-\)almost everywhere, \(D_n^{-}u\) is defined \(\nu _n^{-}-\)almost everywhere and \(D_n^{2}u\) is defined \(\nu _n-\)almost everywhere.

3.2 Left Hand Side Clamped Inextensible Beam

A placement function u is said to be admissible for a left hand side clamped beam if the following condition holds:

$$\begin{aligned} u(0)=0\qquad \text {and}\qquad D_n^{+}u(0)=\mathrm{e}_1. \end{aligned}$$
(5)

It is said to be admissible for an inextensible beam if the following condition holds: \( \Vert u({\scriptstyle {\frac{i+1}{n}}})-u({\scriptstyle {\frac{i}{n}}})\Vert ={\scriptstyle {\frac{1}{n}}}. \) for \(i=0,1, ... ,n-1\). This condition can be written

$$\begin{aligned} \Vert D_n^{+}u \Vert =1\quad \nu _n^{+}-\text {almost everywhere} \end{aligned}$$
(6)

3.3 Deformation Energy Associated with Three Points Interactions

At each node \({\scriptstyle {\frac{i}{n}}}\), for \(i=1, \dots , n-1\), a rotational spring is placed, whose deformation energy depends on the angle \(\theta _n(u)({\scriptstyle {\frac{i}{n}}})\in (-\pi ,+\pi )\) formed by the vectors \(u({\scriptstyle {\frac{i+1}{n}}})-u({\scriptstyle {\frac{i}{n}}})\) and \(u({\scriptstyle {\frac{i}{n}}})-u({\scriptstyle {\frac{i-1}{n}}})\). This energy must vanish when the angle is zero. We assume, following [39, 40], that this energy is proportional to \(1-\cos (\theta _n(u)({\scriptstyle {\frac{i}{n}}}))\). Hence, when the discrete system is in the configuration described by the bounded measure \(\mu (dt)=u(t)\overline{\nu }_n(dt)\), its energy is given by

$$\begin{aligned} E_n^{3}(\mu ):={\frac{1}{n}}\sum _{i=1}^{n-1} n^{2}(1-\cos \theta _n(u)({\scriptstyle {\frac{i}{n}}})) \quad \text {where}\quad \cos \theta _n(u)({\scriptstyle {\frac{i}{n}}}) = \frac{D_n^{+}u({\scriptstyle {\frac{i}{n}}})\cdot D_n^{-}u({\scriptstyle {\frac{i}{n}}})}{\Vert D_n^{+}u({\scriptstyle {\frac{i}{n}}})\Vert \Vert D_n^{-}u({\scriptstyle {\frac{i}{n}}})\Vert } \end{aligned}$$

or, equivalently,

$$\begin{aligned} E_n^{3}(\mu ) =\frac{1}{2}\int \left\| n\biggr ( \frac{D_n^{+}u(t)}{\Vert D_n^{+}u(t)\Vert }-\frac{D_n^{-}u(t)}{\Vert D_n^{-}u(t)\Vert } \biggr ) \right\| ^{2}\, \nu _n(dt). \end{aligned}$$

The above energy is well defined if the placement function u is such that \( D_n^{+}u\ne 0\) \(\nu _n^{+}-\)almost everywhere. This is clearly the case when u is admissible for an inextensible beam. In this case, the discrete energy has the reduced form

$$\begin{aligned} E_n^{3}(\mu ) =\frac{1}{2}\int \Vert D^{2}_n u(t) \Vert ^{2}\, \nu _n(dt). \end{aligned}$$
(7)

4 From Micro to Macro Model: \(\varGamma \)-Convergence Result

This section is devoted to left hand side clamped inextensible beams.

4.1 Functionals Associated to the Micro Model

Let \({\mathscr {M}}_n\) denote the set of those vector bounded measures of the form \(\mu (dt)=u(t)\overline{\nu }_n(dt)\in ({\mathscr {M}}[0,1])^{d}\) such that

$$\begin{aligned} u(0)=0,\quad D_n^{+}u(0)=\mathrm{e}_1 \quad \text {and}\quad \Vert D_n^{+}u\Vert =1\quad \nu _n^{+}-\text {almost everywhere.} \end{aligned}$$
(8)

The total energy functional (associated to the discrete model) is given by

$$\begin{aligned} E_n(\mu ):= {\left\{ \begin{array}{ll} \frac{1}{2}\int \Vert D_n^{2}u(t)\Vert ^{2}\, \nu _n(dt) &{}\text {if}\, \mu (dt)=u(t)\overline{\nu }_n (dt)\in {\mathscr {M}}_n,\\ +\infty &{}\text{ otherwise. } \end{array}\right. } \end{aligned}$$
(9)

4.2 Functional Associated to the Macro Model

Let \(H^{2}(0,1)\) denote the usual Sobolev space. Relying on well-known embedding theorems, any function \(u\in H^{2}(0,1)\) will be considered as a \(C^{1}[0,1]\)-function. Let \({\mathscr {M}}\) be the set of those vector bounded measures of the form \(\mu (dt)=u(t)dt\in ({\mathscr {M}}[0,1])^{d}\) with \(u\in (H^{2}((0,1))^{d}\) and such that

$$\begin{aligned} u(0)=0, \quad u'(0)=\mathrm{e}_1 \quad \text {and}\quad \Vert u'(t)\Vert =1\ \text { for every }\ t\in [0,1]. \end{aligned}$$
(10)

The total energy functional (associated to the continuous model) is given by

$$\begin{aligned} E(\mu ):= {\left\{ \begin{array}{ll} \frac{1}{2}\int _0^1 \Vert u''(t)\Vert ^{2}\, dt &{} \text {if }\mu (dt)=u(t)dt\in {\mathscr {M}},\\ +\infty &{}\text {otherwise.} \end{array}\right. } \end{aligned}$$
(11)

4.3 \(\varGamma -\)Convergence result

Our main result is the following:

Theorem 1

The sequence \((E_n)\) satisfies the relative compactness property and \(\varGamma \)-converges to the functional E.

If we compare Theorem 4.1 with the results proved in [41], the difficulty consists in the fact that the beam is inextensible, which corresponds to a nonlinear constraint.

5 Proof of the Main Result

5.1 Approximation of a Sequence with Bounded Energy

Let \((\mu _n)\) be a sequence in \(({\mathscr {M}}(0,1])^{d}\) with bounded energy. This means that there exists some positive real number M such that

$$\begin{aligned} \mu _n(dt)=u_n(t)\overline{\nu }_n (dt)\in {\mathscr {M}}_n \quad \text {and}\quad \int \Vert D_n^{2}u_n(t)\Vert ^{2}\, \nu _n(dt)\le M. \end{aligned}$$
(12)

for every integer n. Let us define the sequence \((\overline{\mu }_n)\) by setting \(\overline{\mu }_n(dt)=\overline{u}_n(t)dt\), with \(\bar{u}_n\) piecewise \(C^2\) in (0, 1) satisfying:

$$\begin{aligned} \overline{u}_n(0)&= 0 \quad \text {,}\quad \overline{u}_n'(0) = \mathrm{e}_1\\ \overline{u}_n''(t)&= D^{2} u_n({\scriptstyle {\frac{i}{n}}}) \qquad \text {as soon as }t\in ({\scriptstyle {\frac{i}{n}}}-{\scriptstyle {\frac{1}{2n}}} ,{\scriptstyle {\frac{i}{n}}}+{\scriptstyle {\frac{1}{2n}}}). \end{aligned}$$

Notice that \(\overline{u}_n\in (H^{2}(0,1))^{d}\) but in general \(\overline{u}_n\notin {\mathscr {M}}\) because \(\Vert u'_n(t)\Vert \) is not necessarily equal to 1. The following result will be used to establish the lower bound inequality.

Lemma 1

Let \((\mu _n)\) be a sequence in \(({\mathscr {M}}(0,1])^{d}\) with bounded energy. Then, the sequence \((\overline{u}_n)\) defined above is bounded with respect to the usual \(H^{2}-\)norm and satisfies the following properties.

$$\begin{aligned}&\int _{0}^{1} \Vert \overline{u}_n''(t)\Vert ^{2}\, dt =\int \Vert D_n^{2}u_n(t)\Vert ^{2}\, \nu _n(dt)\qquad \text {for every }n, \end{aligned}$$
(13)
$$\begin{aligned}&\lim _{n\rightarrow \infty } \Vert \overline{u}_n'(t)\Vert =1 \qquad \text {for every }\ t\in [0,1],\end{aligned}$$
(14)
$$\begin{aligned}&\ \overline{\mu }_n-\mu _n\ \text {converges to }0\ \text {with respect to the weak}^*\text{ topology. } \end{aligned}$$
(15)

Proof

One has \(\overline{u}_n(0)=0\), \(\overline{u}'_n(0)=\mathrm{e}_1\) and

$$ \int _{0}^{1}\Vert \overline{u}_n''(t)\Vert ^{2}\, dt = \sum _{i=1}^{n-1} \int _{ {\scriptstyle {\frac{i}{n}}}-{\scriptstyle {\frac{1}{2n}}} } ^{{\scriptstyle {\frac{i}{n}}}+{\scriptstyle {\frac{1}{2n}}} } \Vert \overline{u}_n''(t)\Vert ^{2} dt = \int \Vert D^{2}_nu_n (t)\Vert ^{2}\nu _n(dt)\le M $$

which implies that the sequence \((\overline{u}_n)\) is bounded with respect to the usual \(H^{2}-\) norm. Hence, the two sequences \((\overline{u}'_n)\) and \((\overline{u}_n)\) are equicontinuous on [0, 1] and uniformly bounded on [0, 1]. More precisely, for any \(s,t\in [0,1]\),

$$\begin{aligned} \Vert \overline{u}'_n(t)-\overline{u}_n'(s)\Vert \le \sqrt{M}\sqrt{\vert t-s\vert } \quad \text {and}\quad \Vert \overline{u}_n'(t)\Vert \le 1+\sqrt{M}, \end{aligned}$$
(16)
$$\begin{aligned} \Vert \overline{u}_n(t)-\overline{u}_n(s)\Vert \le (1+\sqrt{M}){\vert t-s\vert } \quad \text {and}\quad \Vert \overline{u}_n(t)\Vert \le 1+\sqrt{M}. \end{aligned}$$
(17)

On the other hand, a first computation gives that for any \(i=1, ... ,n-1\),

$$ \overline{u}_n'({\scriptstyle {\frac{i}{n}+\frac{1}{2n}}}) =\mathrm{e}_1+ \int _{0}^{\frac{i}{n}+\frac{1}{2n}}\overline{u}_n''(t)\, dt =\mathrm{e}_1+ \frac{1}{n}\sum _{k=1}^{i} D_n^{2}u_n({\scriptstyle {\frac{k}{n}}}) = D_n^{+}u_n({\scriptstyle {\frac{i}{n}}}). $$

Since \(\Vert D_n^{+}u_n\Vert =1\) \(\nu _n^{+}-\)almost everywhere and the sequence \((\overline{u}_n')\) is equicontinuous on [0, 1], we obtain (14).

A second computation gives \(\overline{u}_n(1)=u_n(1)\) and

$$\begin{aligned} \overline{u}_n({\scriptstyle {\frac{i}{n}}})&= {\scriptstyle {\frac{i}{n}}}\mathrm{e}_1+ \int _{0}^{{\scriptstyle {\frac{i}{n}}}} ({\scriptstyle {\frac{i}{n}}}-s)\overline{u}_n''(s)ds \\&= {\scriptstyle {\frac{i}{n}}}\mathrm{e}_1+ \frac{1}{n}\sum _{k=1}^{i-1} \Biggr ( n\int _{ {\scriptstyle {\frac{k}{n}}}-{\scriptstyle {\frac{1}{2n}}}}^{{\scriptstyle {\frac{k}{n}}}+{\scriptstyle {\frac{1}{2n}}}} ({\scriptstyle {\frac{i}{n}}}-s)\, ds \Biggr ) D_n^{2}u_n({\scriptstyle {\frac{k}{n}}}) +\Biggr (\int _{{\scriptstyle {\frac{i}{n}}}-{\scriptstyle {\frac{1}{2n}}}}^{\scriptstyle {\frac{i}{n}}} ({\scriptstyle {\frac{i}{n}}}-s)\, ds\biggr )D_n^{2}u_n({\scriptstyle {\frac{i}{n}}}) \\&= {\scriptstyle {\frac{i}{n}}}\mathrm{e}_1+ \frac{1}{n}\sum _{k=1}^{i-1} \big ({\scriptstyle \frac{i-k}{n}} \big ) D_n^{2}u_n({\scriptstyle {\frac{k}{n}}}) + \frac{1}{8n^{2}}D_n^{2}u_n({\scriptstyle {\frac{i}{n}}})\\&= u_n({\scriptstyle {\frac{i}{n}}})+ \frac{1}{8n^{2}}D_n^{2}u_n({\scriptstyle {\frac{i}{n}}}) \end{aligned}$$

for every \(i=1, ... ,n-1\). As a consequence, the inequality \(\Vert \overline{u}_n-u_n\Vert \le \frac{\sqrt{M}}{8n}\) holds \(\overline{\nu }_n-\)almost everywhere.

Let \(\varphi \in C([0,1])^{2}\). A third computation gives

$$\begin{aligned} \vert \langle \overline{\mu }_n -\mu _n ,\varphi \rangle \vert&= \left| \sum _{i=1}^{n} \int _{\frac{i-1}{n}}^{\frac{i}{n}} \big ( \varphi (t)\cdot \overline{u}_n(t) -\varphi ({\scriptstyle {\frac{i}{n}}})\cdot u_n({\scriptstyle {\frac{i}{n}}})\big )\, dt \right| \\&\le \sum _{i=1}^{n} \int _{\frac{i-1}{n}}^{\frac{i}{n}} \Vert \varphi (t)\Vert \Vert \overline{u}_n(t) -\overline{u}_n({\scriptstyle {\frac{i}{n}}})\Vert \, dt + \sum _{i=1}^{n} \int _{\frac{i-1}{n}}^{\frac{i}{n}} \Vert \varphi (t)-\varphi ({\scriptstyle {\frac{i}{n}}})\Vert \Vert \overline{u}_n({\scriptstyle {\frac{i}{n}}})\Vert \, dt \\&+\int \Vert \varphi (t)\Vert \Vert \overline{u}_n(t)-u_n(t)\Vert \nu _n(dt)\\&\le \frac{1+\sqrt{M}}{n}\int _{0}^{1}\Vert \varphi (t) \Vert \, dt +(1+\sqrt{M})\sum _{i=1}^{n}\int _{\frac{i-1}{n}}^{\frac{i}{n}} \Vert \varphi (t)-\varphi ({\scriptstyle {\frac{i}{n}}})\Vert \, dt \\&+\frac{\sqrt{M}}{8n}\int \Vert \varphi (t)\Vert \nu _n(dt). \end{aligned}$$

Since

$$ \lim _{n\rightarrow \infty }\sum _{i=1}^{n}\int _{\frac{i-1}{n}}^{\frac{i}{n}} \Vert \varphi (t)-\varphi ({\scriptstyle {\frac{i}{n}}})\Vert \, dt=0 \quad \text {and}\quad \lim _{n\rightarrow \infty } \int \Vert \varphi (t)\Vert \, \nu _n(dt) =\int _{0}^{1} \Vert \varphi (t)\Vert \, dt. $$

we conclude that the sequence \((\overline{\mu }_n-\mu _n)\) converges to 0 with respect to the weak\(^{*}-\)topology of \(({\mathscr {M}}[0,1])^{d}\). The proof is complete.

5.2 The Proof of Theorem 4.1

We divide this proof in three steps.

Step 1. (Relative compactness). Let \(\mu (dt):=u(t)\overline{\nu }_n(dt)\in {\mathscr {M}}_n\). Since \(\Vert u(0)\Vert =0\) and \(\Vert D_n^{+}u\Vert =1\) \(\nu _n^{+}-\) almost everywhere, one has \(\Vert u\Vert \le 1\) \(\overline{\nu }_n-\)almost everywhere, hence

$$ \Vert \mu \Vert _{{\mathscr {M}}} =\int \Vert u(t)\Vert \, \overline{\nu }_n (dt)\le 1. $$

Step 2. (Upper bound inequality). Let \(\mu (dt):=u(t)dt\in {\mathscr {M}}\). Since \(u\in (C^{1}[0,1])^{d}\), we define \( \mu _n(dt)= u_n(t)\overline{\nu }_n(dt)\) by setting

$$ u_n(0)=0 \quad \text { and}\quad u_n({\scriptstyle {\frac{i}{ n}}}) ={\frac{1}{ n}}\sum _{k=0}^{i-1}u'({\scriptstyle {\frac{k}{n}}}) \quad (\text {for}\ i=1, ... ,n). $$

Note that \(D_n^{+} u_n({\scriptstyle \frac{i}{n}})=u'({\scriptstyle \frac{i}{n}})\). Then \(D_n^{+} u_n(0)=\mathrm{e}_1\) and \(\Vert D_n^{+} u_n\Vert =1\) \(\nu _n^{+}\)-almost everywhere. Hence one has \( \mu _n\in {\mathscr {M}}_n \) and

$$ D_n^{2} u_n({\scriptstyle \frac{i}{n}}) =n\big (D_n^{+} u_n({\scriptstyle \frac{i}{n}}) -D_n^{+} u_n({\scriptstyle \frac{i-1}{n}}) \big ) =n\big (u'({\scriptstyle \frac{i}{n}}) -u'({\scriptstyle \frac{i-1}{n}}) \big ) =n\int _{\frac{i-1}{n}}^{\frac{i}{n}}u''(t)\, dt $$

then, using Jensen inequality we obtain

$$ \limsup _{n\rightarrow \infty }\int \Vert D_n^{2} u_n\Vert ^{2}d\nu _n =\limsup _{n\rightarrow \infty }\frac{1}{n}\sum _{k=1}^{n-1} \left\| n\int _{\frac{i-1}{n}}^{\frac{i}{n}}u''(t)\, dt\right\| ^{2} \le \int _{0}^{1}\Vert u''(t)\Vert ^{2}\, dt. $$

Let \(\varphi \in (C[0,1])^{d}\). Since \(u'\) is continuous on [0, 1] we obtain

$$\begin{aligned} \lim _{n\rightarrow \infty }\langle \mu _n,\varphi \rangle&:= \lim _{n\rightarrow \infty }\int \varphi (t)\cdot u_n(t)\, \overline{\nu }_n(dt) \\&=\lim _{n\rightarrow \infty }\frac{1}{n}\sum _{i=1}^{n}\varphi ({\scriptstyle {\frac{i}{n}}}) \cdot \biggr (\frac{1}{n}\sum _{k=0}^{i-1}u'({\scriptstyle {\frac{k}{n}}}) \biggr )\\&=\lim _{n\rightarrow \infty }\frac{1}{n}\sum _{i=1}^{n}\varphi ({\scriptstyle {\frac{i}{n}}}) \cdot \biggr (u({\scriptstyle {\frac{i}{n}}})+ \sum _{k=0}^{i-1}\int _{\frac{k}{n}}^{\frac{k+1}{n}} \big ( u'({\scriptstyle {\frac{k}{n}}})-u'(t)\big )\, dt \biggr )\\&=\lim _{n\rightarrow \infty }\int \varphi (t)\cdot u(t)\overline{\nu }_n(dt) \end{aligned}$$

Hence, Riemann’s Theorem implies that the sequence \((\mu _n)\) converges to \(\mu \) with respect to the weak\(^{*}-\)topology of \(({\mathscr {M}}[0,1])^{d}\).

Step 3. (Lower bound inequality). Let \(\mu , \mu _n\in ({\mathscr {M}}[0,1])^{d}\) such that \((\mu _n)\) converges to \(\mu \) with respect to the weak\(^{*}-\)topology of \(({\mathscr {M}}[0,1])^{d}\). Without loss of generality we may assume that \(\mu _n(dt)=u_n(t)\overline{\nu }_n(dt)\in {\mathscr {M}}_n \) and there exists a nonnegative real number M such that for every n

$$\begin{aligned} \int \Vert D_n^{2}u_n(t)\Vert ^{2} \nu _n(dt)\le M. \end{aligned}$$

Let \((\overline{\mu }_n)\) be the sequence of measures defined in Sect. 5.1. By Lemma 5.1, this sequence converges to \(\mu \) with respect to the weak\(^{*}-\)topology of \(({\mathscr {M}}[0,1])^{d}\). Since \(\overline{\mu }_n(dt)=\overline{u}_n(t)dt\) and the sequence \((\overline{u}_n)\) is bounded with respect to the usual \(H^{2}-\)norm, there exists \(u\in (H^{2}(0,1])^{d}\) such that \(\mu (dt)=u(t)dt\) and

$$ \liminf _{n\rightarrow \infty }\int \Vert D_n^{2}u_n(t)\Vert ^{2}\nu _n (dt)= \liminf _{n\rightarrow \infty }\int _{0}^{1}\Vert \overline{u}_n''(t)\Vert ^{2}dt \ge \int _{0}^{1}\Vert u''(t)\Vert ^{2} dt.$$

Since the space \(H^{2}(0,1)\) is compactly embedded on \(C^{1}[0,1]\), the sequence \((\overline{u}_n')\) converges to \((u')\) with respect to the uniform norm over [0, 1]. Hence, using Lemma 5.1, We obtain

$$\begin{aligned} \Vert u'(t)\Vert =1\qquad \text {for every }\ t\in [0,1] \end{aligned}$$

then \(u\in {\mathscr {M}}\). The proof is complete.

6 Conclusions

We proved a \(\varGamma \)-convergence result for a Hencky-type discretization of an inextensible Euler beam in large deformation regime. Future investigations should generalize the result (in a suitable form) for extensible beam models; moreover, it will be interesting to extend the convergence argument to Generalized Beam Models [42,43,44,45] and also to the dynamics of the discrete system, which should of course take into account the possibility of various kinds of dynamic instabilities [46,47,48]. Finally, it has to be remarked that Hencky-type discretization for Elastica has proven to be very effective, and is in fact used by several computational software packages (as for instance by MATLAB\(^{\circledR }\)). The present result gives a sound mathematical argument which this kind of numerical evidence can be based on.