Multiscale computational homogenisation of shear-flexible beam elements: a Direct FE² approach

Abstract

Structural beam elements are computationally efficient in modelling slender structures. However, they require homogenised material models and computational homogenisation for such elements is complex because it involves higher order kinematics. A Direct FE² homogenisation model for shear-flexible beam elements that is based on the more versatile Timoshenko-Ehrenfest beam theory is presented. Beyond conventional Euler–Bernoulli beam kinematics, an independent shear angle needs to be imposed onto the heterogeneous microscale RVE to govern the microscale shear deformation. It is shown that this can be achieved using an integral constraint involving the moments of axial displacement. With the proposed model, the multiscale analysis can be implemented on commercial FE codes completely as a pre-processing step. Examples presented to demonstrate the performance of the proposed model include 2D and 3D models of fibre reinforced composite beams with material nonlinearity and coupled stretch-twist response. When compared with direct numerical simulations, the proposed model gave closely matching predictions while requiring only a fraction of the computational time. The examples also highlighted the inadequacy of the Euler–Bernoulli beam theory in some cases to further motivate this work.

1 Introduction

Multiscale computational homogenisation is commonly employed to predict the response of a multiphase macroscale structure. Termed FE² by Feyel [1], this strategy has seen wide adoption in the past decade [2,3,4,5,6,7,8,9,10,11]. Beyond nonlinear geometries and materials, it has also been adopted for other engineering analyses, such as rate-dependent responses [12, 13], material damage and failure [14, 15], composite delamination [16], adhesive layers and cohesion [17, 18], magnetism [19] and shape memory alloys [20], among many others. A more comprehensive list of the various applications of the FE² method can be found in the review by Raju et al. [21]. Work has also been done to develop generalised toolboxes for solving multiscale problems in commercial finite element (FE) software, such as ABAQUS [22,23,24].

At its core, conventional FE² methods involve two separate FE analyses—one at the macroscale and another at the microscale—with information exchange between them in a staggered manner [5, 25]. The macroscale kinematic fields are first downscaled to the microscale representative volume element (RVE) at each integration point. The microscale FE analyses on the RVEs are then carried out, following which the responses are then upscaled back to the macroscale FE analysis to complete the solution loop. This requires a considerable level of user involvement to manage the information exchange, even if it is done on a commercial FE software, posing substantial difficulties for less experienced users [26,27,28]. Furthermore, information exchange required by this staggered scheme may result in a significant increase in the wallclock time for some commercial FE software.

A much simpler alternative to the conventional FE² is the Direct FE² method, which was first proposed in 2020 [29]. Using multi-point constraints (MPCs) that are readily available in many commercial FE software, such as ABAQUS, to impose the scale transition kinematics, Direct FE² combines the two FE analyses at different scales into one, transforming it into a monolithic scheme. This eliminates the need for a user-controlled information exchange while the tangent stiffness calculations required for scale transition are handled entirely by the software's internal solver. Direct FE² has seen successful implementation for problems involving geometric and material nonlinearity [29], materials with rate dependency and damage [30], transient analysis [31] and even thermal–mechanical problems [32].

Beyond solid elements that it was originally developed for, Direct FE² as an approach is well-suited to address problems that call for the use of structural elements with heterogeneous material properties. Compared to solid elements, beam and plate elements are computationally more efficient in modelling slender and flat structures. However, the constitutive properties of heterogeneous structures cannot be directly assigned to these elements. Instead, this can only be done by either assigning effective homogenised properties, or through a computational homogenisation framework.

There have been several attempts to incorporate computational homogenisation into beam elements, which is the focus of this paper. For example, Schrefler and Lefik [33] obtained the homogenised material coefficients of heterogeneous structures and combined them with a self-written beam element code to solve problems involving uni-directional composite beams under thermo-mechanical loads. They were able to reduce the size of the problem while predicting stress contours with local features similar to those obtained from standard FE procedures. On the other hand, Cartraud and Messager [34] used the method of cells to solve for the macroscopic response of beams with periodic geometries, including stranded cables with coupling between tension and torsion.

Recently, Xu et al. [35] developed the Direct FE² model for thin plate elements, and by order reduction, slender beam elements. This was based on the Kirchoff-Love plate theory and is applicable to many engineering problems that involve heterogeneous thin plates. Even though its ability to accurately capture the macroscale constitutive properties of thin plates was demonstrated, the wider application of this model as well as the aforementioned beam models is restricted by the underlying assumptions of the Kirchoff-Love plate and Euler–Bernoulli beam theories respectively. Primarily, the theories assume that the cross section of the beam or plate remains perpendicular to its axis and that transverse shear deformations are negligible [36, 37].

A higher order computational homogenisation framework is needed to capture transverse shear deformations for beam and plate elements based on the Timoshenko-Ehrenfest beam and Mindlin-Reissner plate theories respectively. They predict more accurately the constitutive response of thick beams and plates as well as shear-dominant structures such as laminated composites and foam core sandwich structures, which have wide engineering applications [38, 39]. A common difficulty in the development of such higher-order beam and plate homogenisation models is in imposing the shear deformation onto the microscale RVE.

Geers et al. proposed using a second-order framework to implement the computational homogenisation of structured thin sheets with transverse shear [40]. They highlighted that the key issue with such a homogenisation framework involving transverse shear lies in the mismatch of assumptions at difference scales for plate structures. At the macroscale, cross-sections are assumed to remain plane even after deformation. However, the absence of global shear tractions due to the plane-stress assumption at the microscale prevents these cross-sections from remaining plane. To remedy this, they imposed an additional weak constraint on the RVE cross-sections such that the average shear at both scales are the same.

On the other hand, Klarmann et al. proposed using additional kinetic constraints on top of a first-order beam homogenisation framework to impose the shear deformation on the RVE [41]. A detailed breakdown of the scale transition kinematics and kinetics of shear-flexible beam element was provided. It was identified that the RVE would undergo rigid body rotation in the absence of additional constraints. They proposed matching the RVE normal stresses to those predicted from beam theory to prevent this rotation. This was enforced in a weak sense over the RVE face through Lagrange parameters using additional nodes and subsequently implemented as internal constraints. While comprehensive, their homogenisation scheme is numerically more complex to implement and requires a revised stiffness matrix for the RVE finite elements which includes the Lagrange parameters.

We propose an alternative computational homogenisation scheme for shear-flexible beam elements that is simpler to implement based on the Direct FE² framework. The shear angle of the beam is imposed onto the RVE via a kinematic integral constraint that is applied directly onto the RVE boundary nodes. This paper is outlined as follows. In Sect. 2, the kinematic and kinetic relationships across scales required for the proposed Timoshenko Beam Direct FE² model are presented. In Sect. 3, details on how the model is implemented on commercial FE software are shown along with the necessary MPCs and mesh volume scaling. These are followed by the corresponding 3D extensions. In Sect. 4, example problems that demonstrate the necessity of such a model that considers shear deformation are presented, with the results obtained from this proposed model validated against those obtained from Direct Numerical Simulations (DNS) where possible. Finally, we conclude in Sect. 5.

2 Scale transition relations for a shear-flexible beam

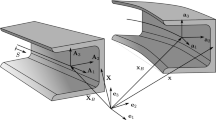
For macroscale beam structures, variations are considered to occur along its axial direction only. Thus, homogenisation is carried out in that direction using through-height and through-depth RVEs as illustrated in Fig. 1. The RVEs for beams are typically located at the mesoscale and will be referred to as such in subsequent sections.

Fig. 1

An illustration of a beam element homogenisation framework a homogenised macroscale beam element, b explicitly modelled RVE

2.1 Macroscale shear-flexible beam

The kinematics of a shear-flexible beam can be described using variables along the beam centreline. Macroscale variables along the centreline will be denoted using ${\left(\cdot \right)}^{c}$, and their gradients along the centreline will be denoted by $\nabla {\left(\cdot \right)}^{c}$. For brevity, a 2D beam on the conventional ${x}_{1}{x}_{3}$-plane will be considered, as the kinematics and kinetics are identical along the ${x}_{1}{x}_{2}$-plane. A 3D beam will be a superposition of both with additional terms for twisting. The macroscale variables in the respective directions will be denoted with subscripts ${\left(\cdot \right)}_{1}$ and ${\left(\cdot \right)}_{3}$.

The macroscale beam continuum of interest is based on the Timoshenko-Ehrenfest beam theory, which takes into account transverse shear in the cross-section rotation, in addition to its centreline slope [42]. Details on the governing equations and some theoretical solutions can be seen in [43]. The key difference compared to the Euler–Bernoulli beam is that cross-sections of the beam are no longer restricted to be perpendicular to the beam centreline. It is now described using a kinematically independent angular term ${\varphi }_{2}$ which rotates about the ${x}_{2}$-axis. The kinematics of any point along the beam are described by the following equations.

$${u}_{1}={u}_{1}^{c}-{x}_{3}{\varphi }_{2}^{c}$$

(1)

$${u}_{3}={u}_{3}^{c}$$

(2)

$${\varphi }_{2}={\varphi }_{2}^{c}$$

(3)

The macroscale external virtual work density per unit length of the beam in the reference configuration is then given by

$$\delta {W}^{den}={N}_{11}\delta \nabla {u}_{1}^{c}+{Q}_{13}\updelta \left(\nabla {u}_{3}^{c}-{\varphi }_{2}^{c}\right)+{M}_{12}\updelta \nabla {\varphi }_{2}^{c}$$

(4)

where ${N}_{11}$ is the axial force, ${Q}_{13}$ the transverse shear force and ${M}_{12}$ the moment.

2.2 Mesoscale RVE

We consider the mesoscale RVE that will be used to derive the effective constitutive behaviour of the macroscale beam. The corresponding mesoscale kinematic and kinetic variables will be denoted as $\widehat{\left(\cdot \right)}$ while their gradients are denoted as ${\widehat{\left(\cdot \right)}}_{,i}$ for $i=\mathrm{1,3}$. Without any loss in generality, we consider a rectangular through-height RVE with dimensions ${h}_{RVE}\times {b}_{RVE}$ as shown in Fig. 1b. Since the deformation of the RVE is driven by kinematic downscaling from the macroscale, the average internal virtual work done per unit length in the RVE arising from its constitutive response is required for subsequent upscaling, and is obtained as

$$\langle \delta {\widehat{W}}_{int}\rangle =\frac{{A}^{cs}}{\widehat{V}}\int {\widehat{\sigma }}_{ij}\delta {\widehat{u}}_{i,j}d\widehat{V}=\frac{{A}^{cs}}{\widehat{V}}\int {\widehat{\sigma }}_{11}\delta {\widehat{u}}_{\mathrm{1,1}}+{\widehat{\sigma }}_{13}\delta {\widehat{u}}_{\mathrm{1,3}}+{\widehat{\sigma }}_{31}\delta {\widehat{u}}_{\mathrm{3,1}}d\widehat{V}$$

(5)

where ${A}^{cs}$ is the cross-sectional area of the beam, $\widehat{{\varvec{\sigma}}}$ is the mesoscale RVE stress tensor, $\widehat{V}$ is the RVE volume and ${\widehat{u}}_{i,j}$ the displacement gradients.

2.3 Downscaling relations

The macroscale to mesoscale kinematic downscaling is based on the requirement that the macroscale deformation can be obtained from the mesoscale average. This defines a set of boundary conditions to be imposed on the mesoscale RVE. Beyond a smoothly varying component defined by the macroscale deformation, the mesoscale deformation field also needs to incorporate a locally fluctuating component to account for the perturbations induced by the heterogeneity of the mesoscale structure. Combining this with the macroscale kinematics described by Eqs. (1) and (2) yields the mesoscale kinematic decomposition.

$${\widehat{u}}_{1}={u}_{1}^{c}-{\widehat{x}}_{3}{\varphi }_{2}^{c}+{\widehat{x}}_{1}\nabla {u}_{1}^{c}-{\widehat{x}}_{3}{\widehat{x}}_{1}\nabla {\varphi }_{2}^{c}+{\widehat{u}}_{1}^{*}$$

(6)

$${\widehat{u}}_{3}={u}_{3}^{c}+{\widehat{x}}_{1}\nabla {u}_{3}^{c}+{\widehat{u}}_{3}^{*}$$

(7)

It is noted that since the RVE will be modelled using solid elements, it will only have ${\widehat{u}}_{1}$ and ${\widehat{u}}_{3}$ displacement degrees of freedom (DOF). The first-order gradient terms in Eqs. (6) and (7) describe the smoothly varying component and ${\widehat{\left(\cdot \right)}}^{*}$ are the perturbation components for each mesoscale kinematic variable. Here, ${\widehat{x}}_{i}$ is the position of a given mesoscale point measured from the centroid of the RVE. This decomposition is based on the assumption that there is a clear separation of scale between the RVE length and the characteristic length within which the applied load changes across the macroscale [26, 44].

2.4 Upscaling relations

Homogenisation strategies enforce the Hill-Mandel condition to ensure that the external and internal work done across scales are consistent [45]. The condition can be satisfied by linear displacement, constant traction boundary conditions or periodic boundary conditions (PBC). PBC is adopted here because it is the most accurate and fastest converging among the three [46,47,48].

To satisfy the Hill-Mandel condition, the macroscale external virtual work density given in Eq. (4) must be equal to the mesoscale average internal virtual work done per unit length in Eq. (5). The mesoscale kinematic decomposition from Eqs. (6) and (7) are first substituted into Eq. (5) to give

$$\langle \delta {\widehat{W}}_{int}\rangle =\frac{{A}^{cs}}{\widehat{V}}\int {\widehat{\sigma }}_{11}\left(\delta \nabla {u}_{1}^{c}-{\widehat{x}}_{3}\delta \nabla {\varphi }_{2}^{c}+\delta {\widehat{u}}_{\mathrm{1,1}}^{*}\right)$$

$$+{\widehat{\sigma }}_{13}\left(-\delta {\varphi }_{2}^{c}-{\widehat{x}}_{1}\delta \nabla {\varphi }_{2}^{c}+\delta {\widehat{u}}_{\mathrm{1,3}}^{*}\right)+{\widehat{\sigma }}_{31}\left(\updelta \nabla {u}_{3}^{c}+\delta {\widehat{u}}_{\mathrm{3,1}}^{*}\right) d\widehat{V}$$

(8)

Grouping the perturbation terms together,

$$\langle \delta {\widehat{W}}_{int}\rangle =\frac{{A}^{cs}}{\widehat{V}}\int {\widehat{\sigma }}_{11}\nabla \delta {u}_{1}^{c}+{\widehat{\sigma }}_{31}\nabla\updelta {u}_{3}^{c}-{\widehat{\sigma }}_{13}\delta {\varphi }_{2}^{c}+\left(-{\widehat{\sigma }}_{11}{\widehat{x}}_{3}-{\widehat{\sigma }}_{13}{\widehat{x}}_{1}\right)\nabla \delta {\varphi }_{2}^{c}d\widehat{V}$$

$$ \qquad\qquad \quad \; +\frac{{A}^{cs}}{\widehat{V}}\int {\widehat{\sigma }}_{11}\delta {\widehat{u}}_{\mathrm{1,1}}^{*}+{\widehat{\sigma }}_{13}\delta {\widehat{u}}_{\mathrm{1,3}}^{*}+{\widehat{\sigma }}_{31}\delta {\widehat{u}}_{\mathrm{3,1}}^{*}d\widehat{V}$$

$$\qquad \qquad =\frac{{A}^{cs}}{\widehat{V}}\int {\widehat{\sigma }}_{11}\nabla \delta {u}_{1}^{c}+{\widehat{\sigma }}_{31}\nabla\updelta {u}_{3}^{c}-{\widehat{\sigma }}_{13}\delta {\varphi }_{2}^{c}+\left(-{\widehat{\sigma }}_{11}{\widehat{x}}_{3}-{\widehat{\sigma }}_{13}{\widehat{x}}_{1}\right)\nabla \delta {\varphi }_{2}^{c}d\widehat{V}$$

$$\qquad \qquad \quad+\frac{{A}^{cs}}{\widehat{V}}\int {\widehat{t}}_{1}\delta {\widehat{u}}_{1}^{*}+{\widehat{t}}_{3}\delta {\widehat{u}}_{3}^{*}d\widehat{S}$$

(9)

The second integral of Eq. (9) vanishes for zero displacement perturbations or constant tractions on $\widehat{S}$, as well as for periodic boundary conditions. The elimination of this term for the case where the top and bottom surfaces of the beam are traction free, together with periodicity in the ${\widehat{x}}_{1}$ direction has been shown in [35]. The average internal virtual work done per unit length is then simplified to

$$\langle \delta {\widehat{W}}_{int}\rangle =\frac{{A}^{cs}}{\widehat{V}}\int {\widehat{\sigma }}_{11}\delta \nabla {u}_{1}^{c}+{\widehat{\sigma }}_{13}\updelta \left(\nabla {u}_{3}^{c}-{\varphi }_{2}^{c}\right)+\left(-{\widehat{\sigma }}_{11}{\widehat{x}}_{3}-{\widehat{\sigma }}_{13}{\widehat{x}}_{1}\right)\nabla \delta {\varphi }_{2}^{c}d\widehat{V}$$

(10)

A direct comparison between Eqs. (10) and (4) yields the homogenised macroscale forces in terms of the mesoscale kinetic terms.

$${N}_{11}=\frac{{A}^{cs}}{\widehat{V}}\int {\widehat{\sigma }}_{11}d\widehat{V}$$

(11)

$${N}_{13}=\frac{{A}^{cs}}{\widehat{V}}\int {\widehat{\sigma }}_{13}d\widehat{V}$$

(12)

$${M}_{12}=\frac{{A}^{cs}}{\widehat{V}}\int \left(-{\widehat{\sigma }}_{11}{\widehat{x}}_{3}-{\widehat{\sigma }}_{13}{\widehat{x}}_{1}\right)d\widehat{V}$$

(13)

In conventional FE² methods, these homogenised forces need to be upscaled as the macroscale nodal forces. In Direct FE² however, the macroscale and mesoscale DOF are directly linked and solved within the same FE iteration loop, hence a separate extraction is not needed.

3 Implementation of the Direct FE² model

In this section, the implementation of the proposed Timoshenko Beam Direct FE² model on commercial FE software is presented. A quadratic shear-flexible beam element (ABAQUS B22) with two integration points is chosen as the macroscale beam element. This 3-noded beam element with a selective reduced integration scheme avoids shear locking and has been shown to give a good approximation to the theoretical solution [49]. Two explicitly modelled RVEs are then superimposed onto each beam element, with their centroids coinciding with the integration points of the beam element, i.e., both macroscale and mesoscale FE meshes appear on top of each other in the same FE model. Material properties are assigned only to the mesoscale elements while the macroscale elements have null properties.

3.1 Scale transition kinematic constraints

The kinematic constraints linking the macroscale and mesoscale DOF are implemented by imposing onto the RVE boundary nodes the PBCs as described by the macroscale DOF. Based on the mesoscale kinematic decomposition presented in Eqs. (6) and (7), the PBCs for ${\widehat{u}}_{1}$ and ${\widehat{u}}_{3}$ can be written as

$${\widehat{u}}_{1}{|}_{R}-{\widehat{u}}_{1}{|}_{L}={b}_{RVE}\left(\nabla {u}_{1}^{c}-{\widehat{x}}_{3}\nabla {\varphi }_{2}^{c}\right)$$

(14)

$${\widehat{u}}_{3}{|}_{R}-{\widehat{u}}_{3}{|}_{L}={b}_{RVE}\left(\nabla {u}_{3}^{c}\right)$$

(15)

where $\left(\cdot \right){|}_{R}$ and $\left(\cdot \right){|}_{L}$ refer to the right and left boundaries of the RVE respectively.

An additional set of constraints is required to prevent rigid body translation of the RVE. This is done by prescribing the RVE centroid to translate together with the beam integration point where it is located, i.e.,

$${\widehat{u}}_{i}{|}_{centroid}={u}_{i}^{c}{|}_{int pt} for i=\mathrm{1,3}$$

(16)

With that, the complete set of PBCs and rigid body constraints can then be imposed onto the mesoscale RVE. Based on the discretisation of the RVE, the PBCs and rigid body constraints in Eqs. (14)–(16) can be respectively rewritten as

$${\widehat{u}}_{1}^{iR}={\widehat{u}}_{1}^{iL}+{b}_{RVE}\sum\limits_{j=1}^{3}{N}_{j,1}{u}_{1}^{j}+{b}_{RVE}{\widehat{x}}_{3} \sum\limits_{j=1}^{3}{N}_{j,1}{\varphi }_{2}^{j}$$

(17)

$${\widehat{u}}_{3}^{iR}={\widehat{u}}_{3}^{iL}+{b}_{RVE}\sum\limits_{j=1}^{3}{N}_{j,1}{u}_{3}^{j}$$

(18)

$${\widehat{u}}_{i}^{centroid}=\sum\limits_{j=1}^{3}{N}_{j}{u}_{i}^{j}$$

(19)

where ${\left(\cdot \right)}^{iL}$ and ${\left(\cdot \right)}^{iR}$ in Eqs. (17) and (18) refer to the nodes in the ${i}{\text{th}}$ corresponding pair between the left and right boundaries respectively, ${\left(\cdot \right)}^{j}$ refers to the ${j}{\text{th}}$ node on the macroscale beam element and ${N}_{j}$ refers to the quadratic shape function attributed to that particular node. Equations (17)–(19) link the macroscale and mesoscale DOF and can be directly implemented as MPCs in ABAQUS [50]. This is done completely at the pre-processing stage.

The above equations are similar to those derived in [35] and further details can be seen therein, with the key difference being the shape functions used. In this proposed framework, interpolation is done using quadratic shape functions arising from the 3-node macroscale beam element chosen instead of the Hermite interpolation functions commonly used for non-shear-flexible beam and plate elements.

The constraint equations can be similarly obtained for a 3D macroscale beam and will be presented in brief here. In 3D models, the beam element has six DOF, namely ${u}_{1},{u}_{2}, {u}_{3}, {\varphi }_{1}, {\varphi }_{2}$ and ${\varphi }_{3}$, with the last three corresponding to rotations about the $1, 2$ and $3$ axes respectively. Using a first-order decomposition similar to the 2D beam and taking into account perturbations introduced by the mesoscale heterogeneities, the PBC equations for the mesoscale RVE can be written as

$${\widehat{u}}_{1}{|}_{R}-{\widehat{u}}_{1}{|}_{L}={b}_{RVE}\left(\nabla {u}_{1}^{c}-{\widehat{x}}_{2}\nabla {\varphi }_{3}^{c}+{\widehat{x}}_{3}\nabla {\varphi }_{2}^{c}\right)$$

(20)

$${\widehat{u}}_{2}{|}_{R}-{\widehat{u}}_{2}{|}_{L}={b}_{RVE}\left(\nabla {u}_{2}^{c}-{\widehat{x}}_{3}\nabla {\varphi }_{1}^{c}\right)$$

(21)

$${\widehat{u}}_{3}{|}_{R}-{\widehat{u}}_{3}{|}_{L}={b}_{RVE}\left(\nabla {u}_{3}^{c}+{\widehat{x}}_{2}\nabla {\varphi }_{1}^{c}\right)$$

(22)

In Eqs. (21) and (22), the second term on the RHS are deformations due to twisting in the macroscale beam element, quantified by the gradient of the axial rotation of the beam, $\nabla {\varphi }_{1}^{c}$. These terms do not appear in the 2D beam model. Equations (20)–(22) can then be rewritten in terms of the nodal DOFs as before.

$${\widehat{u}}_{1}^{iR}={\widehat{u}}_{1}^{iL}+{b}_{RVE}\sum\limits_{j=1}^{3}{N}_{j,1}{u}_{1}^{j}-{b}_{RVE}{\widehat{x}}_{2}\sum\limits_{j=1}^{3}{N}_{j,1}{\varphi }_{3}^{j}+{b}_{RVE}{\widehat{x}}_{3}\sum\limits_{j=1}^{3}{N}_{j,1}{\varphi }_{2}^{j}$$

(23)

$${\widehat{u}}_{2}^{iR}={\widehat{u}}_{2}^{iL}+{b}_{RVE}\sum\limits_{j=1}^{3}{N}_{j,1}{u}_{2}^{j}-{b}_{RVE}{\widehat{x}}_{3}\sum\limits_{j=1}^{3}{N}_{j,1}{\varphi }_{1}^{j}$$

(24)

$${\widehat{u}}_{3}^{iR}={\widehat{u}}_{3}^{iL}+{b}_{RVE}\sum\limits_{j=1}^{3}{N}_{j,1}{u}_{3}^{j}+{b}_{RVE}{\widehat{x}}_{2}\sum\limits_{j=1}^{3}{N}_{j,1}{\varphi }_{1}^{j}$$

(25)

The rigid body constraints can also be similarly expressed,

$${\widehat{u}}_{i}^{centroid}=\sum\limits_{j=1}^{3}{N}_{j}{u}_{i}^{j}$$

(26)

$${\widehat{u}}_{3}^{A}={\widehat{u}}_{3}^{centroid}+{\widehat{x}}_{2}^{A}\sum\limits_{j=1}^{3}{N}_{j}{\varphi }_{1}^{j}$$

(27)

where Eq. (27) constrains the RVE against rigid body rotation along the beam axis. It is imposed on a point, A, in the RVE that is ${\widehat{x}}_{2}^{A}$ offset from the centroid along the ${x}_{2}$ direction. Equations (23)–(27) can then be similarly written as MPCs and implemented in ABAQUS to tie the macroscale and mesoscale DOF.

3.2 Satisfaction of the Hill-Mandel condition

The other step in implementation of the Direct FE² homogenization is the scaling of the RVEs to satisfy the Hill-Mandel condition. Consider the total internal virtual work done for each beam element,

$$\delta {W}_{int}=\int \delta {W}_{int}^{den}dL=\sum\limits_{\alpha }{\omega }_{\alpha }{J}_{\alpha }{\left(\delta {W}_{int}^{den}\right)}_{\alpha }$$

(28)

where ${\left(\cdot \right)}_{\alpha }$ denotes quantities at an integration point, and $\omega$ and $J$ are the weights and Jacobian at the integration points respectively. The Hill-Mandel condition requires that the internal virtual work done at each macroscale integration point to be equal to the average internal virtual work done in the RVE located there. Substituting Eqs. (5) into (28) yields

$$\delta {W}_{int}=\sum\limits_{\alpha }\frac{{\omega }_{\alpha }{J}_{\alpha }{A}^{cs}}{{\widehat{V}}_{\alpha }}{\int }_{{\left(RVE\right)}_{\alpha }}{\widehat{\sigma }}_{ij}\delta {\widehat{u}}_{i,j}d\widehat{V}$$

(29)

In Direct FE², the commonly used strategy is to scale the volume of the RVE, ${\widehat{V}}_{\alpha }$, such that the coefficient $\left(\frac{{\omega }_{\alpha }{J}_{\alpha }{A}^{cs}}{{\widehat{V}}_{\alpha }}\right)$ is unity. The macroscale work done is then the total internal strain energies at of all the mesoscale RVEs, as shown in Eq. (29). As suggested by Tan et al. [29], this can be achieved at the pre-processing stage by changing the RVE section thickness for 2D analyses or by scaling the mesh volume of the entire RVE for 3D analyses, i.e.,

$${\widehat{V}}_{\alpha }={\omega }_{\alpha }{J}_{\alpha }{A}^{cs}$$

(30)

It should be noted that volume scaling does not increase computational cost. As shown in Fig. 2, if all dimensions of the RVE is to be scaled by $n$ to satisfy Eq. (30), all elements are also scaled accordingly. The number of nodes and elements in the RVE mesh as well as their connectivity remain unchanged. As such, the total degrees of freedom in the problem remain unchanged as well.

Fig. 2

Illustration of uniform volume scaling of the RVE mesh by a factor of $n$ in all directions

Note that in conventional FE², Eqs. (11)–(13) are needed to identify the stresses to upscale in order to satisfy the Hill-Mandel condition. In Direct FE², energy consistency is enforced simply by scaling the RVE energy through scaling the RVE volume according to Eq. (30). Equations (11)–(13) are not required, but are presented nevertheless to demonstrate the consistency with conventional upscaling approaches.

3.3 Higher-order shear angle constraint

As reported by Klarmann et al. [41], imposing shear deformations onto the RVE under simple PBCs would result in spurious rotations. In other words, the set of constraints in Eqs. (17)–(19) obtained from first-order homogenisation alone are insufficient to completely describe the RVE boundary value problem. This is because the shear angle does not appear in any of the constraint equations in Sect. 3.1 and is hence not imposed at the mesoscale.

To resolve this, we propose to match the moments of ${\widehat{u}}_{1}$ and ${u}_{1}$ about the centroidal axis in an average sense, i.e.,

$$\int {\widehat{x}}_{3}{\widehat{u}}_{1}d{\widehat{x}}_{3}=\int {\widehat{x}}_{3}{u}_{1}d{\widehat{x}}_{3}$$

(31)

Using Eq. (1) for the macroscale axial displacement and performing the integration on the RHS, we obtain the constraint

$$\int {\widehat{x}}_{3}{\widehat{u}}_{1}d{\widehat{x}}_{3}=-\frac{{\left({h}_{RVE}\right)}^{3}}{12}{\varphi }_{2}^{c}$$

(32)

Details on the thought process that led to this choice of constraint are presented in “Appendix A”. It should be noted that a similar constraint was also mentioned in Geers et al. [40]. In the proposed Direct FE² model, Eq. (32) is imposed onto the left boundary of the RVE. For implementation into ABAQUS as an MPC, it is rewritten in the discretised form as

$$\sum\limits_{i=1}^{N}{a}^{i}{\widehat{u}}_{1}^{i}=-\frac{{\left({h}_{RVE}\right)}^{3}}{12}\sum\limits_{j=1}^{3}\left[{N}_{j}+\left(-\frac{{b}_{RVE}}{2}\right){N}_{j,1}\right]{\varphi }_{2}^{j}$$

(33)

where

$${a}^{i}=\int {\widehat{x}}_{3}{N}_{i}d{\widehat{x}}_{3}$$

(34)

and ${N}_{i}$ is the shape function of node $i$ on the mesoscale RVE boundary.

This constraint is similarly extended to the 3D beam model. Here, one constraint is required for each shear angle. They take the form

$$\int {\int }_{Left}{\widehat{x}}_{3}{\widehat{u}}_{1}d\widehat{S}=\left[{\left({\varphi }_{2}^{c}\right)}_{int pt}+\left(-\frac{{b}_{RVE}}{2}\right)\nabla {\varphi }_{2}^{c}\right]\left[\frac{{\left({h}_{RVE}\right)}^{3}\left({t}_{RVE}\right)}{12}\right]$$

(35)

$$\int {\int }_{Left}{\widehat{x}}_{2}{\widehat{u}}_{1}d\widehat{S}=-\left[{\left({\varphi }_{3}^{c}\right)}_{int pt}+\left(-\frac{{b}_{RVE}}{2}\right)\nabla {\varphi }_{3}^{c}\right]\left[\frac{{\left({t}_{RVE}\right)}^{3}\left({h}_{RVE}\right)}{12}\right]$$

(36)

where ${t}_{RVE}$ refers to the dimension of the RVE in the ${x}_{2}$-direction that was previously not considered in the 2D model. It should be noted that the integrals are now surface integrals about the left boundary surface of the RVE, instead of line integrals used in the 2D model. Similarly, Eqs. (35) and (36) can then be written in their respective discretised forms below to be imposed as MPCs.

$$\sum\limits_{i=1}^{N}{b}^{i}{\widehat{u}}_{1}^{i}=\frac{{\left({h}_{RVE}\right)}^{3}\left({t}_{RVE}\right)}{12}{\sum }_{j=1}^{3}\left[{N}_{j}+\left(-\frac{{b}_{RVE}}{2}\right){N}_{j,1}\right]{\varphi }_{2}^{j}$$

(37)

$${\sum }_{i=1}^{N}{c}^{i}{\widehat{u}}_{1}^{i}=-\frac{{\left({t}_{RVE}\right)}^{3}\left({h}_{RVE}\right)}{12}{\sum }_{j=1}^{3}\left[{N}_{j}+\left(-\frac{{b}_{RVE}}{2}\right){N}_{j,1}\right]{\varphi }_{3}^{j}$$

(38)

where,

$${b}^{i}=\int {\int }_{Left}{\widehat{x}}_{3}{N}_{i}d\widehat{S}$$

(39)

$${c}^{i}=\int {\int }_{Left}{\widehat{x}}_{2}{N}_{i}d\widehat{S}$$

(40)

With that, the proposed Timoshenko Beam Direct FE² model is complete. The model is described by Eqs. (17)–(19) and (33) for 2D, and Eqs. (23)–(27), (37) and (38) for 3D, and they are directly imposed as MPCs in ABAQUS to link the macroscale and mesoscale DOF.

3.4 Comparison with the conventional FE² method

Among the various computational homogenisation frameworks, Direct FE² stands out for its ease of implementation. As shown previously, Direct FE² can be implemented on commercial FE codes through only 2 key steps, namely, specifying the MPCs and RVE volume scaling, and both are executed during the pre-processing stage. In contrast, conventional FE² methods entail greater level of user intervention. They often require a separate control script to manage the information transfer between scales for each problem. The tangent stiffness matrix calculations, which can be complex depending on the nature of the problem, will also need to be determined by the users whereas this is handled entirely by the commercial FE code’s internal solver in Direct FE².

Since Direct FE² can be easily implemented on commercial FE codes, another advantage is that it can make full use of the readily available material models as well as other analysis capabilities such as nonlinear large deformation, contact, implicit dynamics [31] and even multi-physics [32].

The difference between conventional and Direct FE² goes beyond how they are implemented. As shown in Fig. 3a, the former comprises two iterative analysis loops—a mesoscale FEA nested inside a macroscale FEA, i.e., the multiscale analysis staggers between macroscale and mesoscale. When implemented on solvers that are not reentrant, such as ABAQUS, staggered schemes suffer significant downtime. The non-reentrant nature means that each iterative loop must be carried out as a separate FE analysis. As such, staggered solution schemes require information to be exchanged between the FE analyses of different scales through constant reading and writing of computational data. Moreover, the lag time associated with the starting of a FE analysis for each iteration can add up considerably. On the other hand, Direct FE² is a monolithic scheme that is performed in a single iterative analysis loop as shown in Fig. 3b. It does not require data exchange between scales and is carried out as a single FE analysis, thus avoiding all the downtime mentioned. However, it is noted that the pre-processing time in Direct FE² would be slightly longer for the MPC equations between scales to be set up.

Fig. 3

Schematic of iteration loop a conventional FE², b direct FE²

A comprehensive comparison of computational performance between staggered and monolithic schemes was conducted by Lange et al. [51], who proposed another monolithic FE² scheme. By using an in-house FORTRAN code as the microscale solver and integrating it with the macroscale solver in ABAQUS through its UMAT interface, the downtime associated with non-reentrant solvers for the staggered scheme was circumvented. The examples they presented still showed that the monolithic scheme consistently outperforms the staggered scheme, with savings in computational costs ranging from 40 to 60%. It should be pointed out that their solver included steps to reduce the size and bandwidth of the system of equations through static condensation and renumbering of equations. The implementation of Direct FE² presented here simply leverages on ABAQUS’ solver without incorporating such optimization. Another comparison between conventional and Direct FE² can be found in Raju et al. [21]. Both macroscale and microscale FEA of the conventional FE² were solved on ABAQUS with information between scales communicated through files. To discount the downtime due to data exchange and starting ABAQUS repeatedly, only the numbers of floating point operations for computation were used for the evaluation. Direct FE² needed about only 40% the number of operations in conventional FE².

Next, the accuracy and necessity of this proposed Direct FE² model is demonstrated using several example problems.

4 Modelling composite beams using direct FE²

4.1 Single ply composite beam under shear

In the first example, we consider a single ply composite beam subjected to significant transverse shear to demonstrate that under circumstances when the assumptions of the Euler–Bernoulli beam theory no longer hold, homogenisation models based on the Euler beam will be insufficient. For such cases, the proposed Timoshenko Beam Direct FE² model is required to capture the constitutive responses accurately.

The beam is fixed at both ends and subjected to a downward displacement at the midpoint as shown in Fig. 4. Based on the symmetry of the problem, only the left-half of the beam is modelled. The beam is modelled with both an Euler Beam Direct FE² (EBeam) model as well as the proposed Timoshenko Beam Direct FE² (TBeam) model. The results from both Direct FE² models are benchmarked against a DNS model using solid elements (Fig. 5).

Fig. 4

Single ply composite beam under shear a schematic showing problem geomtry and loading conditions, b explicitly modelled RVE of the beam

Fig. 5

DNS and Direct FE² models with loads and boundary conditions for single ply composite beam

The beam consists of an elasto-plastic epoxy matrix with properties taken from [30] and carbon fibres that are assumed to be elastic (Table 1). An RVE of the beam can be seen in Fig. 4b. Each RVE has 160 fibres with a diameter of 0.04 mm, resulting in a fibre volume fraction of 0.402. The fibres are randomly distributed, subjected to a minimum distance between them and periodicity is enforced at the boundaries along the axial direction of the beam. The RVE is modelled with solid plane-stress elements (ABAQUS CPS4). The DNS model is obtained by tessellating the RVE, while the two Direct FE² models are identical, except for the choice of macroscale beam element used and consequently the MPCs that are imposed (Table 2). The TBeam model is constructed using two, three and five macroscale beam elements.

Table 1 Material properties for single ply composite beam under shear

Table 2 Differences between EBeam and TBeam models

The midpoints of the beam models are then subjected to a downward displacement of 1 mm. Since the two Direct FE² models follow the conventional beam assumption of transverse incompressibility, all nodes on the mid-beam cross-section of the DNS model are displaced uniformly to prevent any discrepancies that may arise from stress concentrations due to point loads.

From the force–displacement plot in Fig. 6, it can be seen that only the constitutive response obtained from the TBeam models matches that from the DNS model. This is the case even for the TBeam model using only two macroscale beam elements. The EBeam model is seen to be excessively stiff compared to the DNS model. Since this is a problem where significant shear is expected, the key difference in the response of both Direct FE² models can be attributed to the difference in shear deformation.

Fig. 6

Force–displacement plot of the single ply composite beam

This is supported from the shear stress contours obtained from all three models as shown in Fig. 7. The shear stress contour obtained from the TBeam model is almost identical to that obtained from the DNS model, whereas there is a stress band located around the mid-height of the beam missing in the EBeam model. This would be the expected transverse shear stress from beam theory that peaks at the beam's neutral axis, and is not accounted for in the EBeam model.

Fig. 7

Shear stress contour (Pa) of the single ply composite beam for all three models

In terms of computational efficiency, it is evident from Table 3 that all the Direct FE² models are much more efficient than the DNS model due to the reduced number of DOF arising from homogenisation. Unsurprisingly, a larger extent of homogenisation attained by using fewer macroscale beam elements would result in shorter computation times. For this problem, the CPU time for the TBeam model with two macroscale beam elements is only about 13.2% that for the DNS model.

Table 3 Comparison of CPU time of the single ply composite beam

The study is then extended to investigate the effect of RVE size on the analysis results. The TBeam model with 3 beam elements is repeated using RVEs with widths of 0.125 mm, 0.25 mm and 0.5 mm, as shown in Fig. 8. The number of fibres within each RVE is scaled accordingly such that the fibre volume fraction is maintained at 0.402. Similar to the original RVE, the fibres are randomly distributed, subjected to same minimum distance between them and periodicity is enforced at the boundaries along the axial direction of the beam. As the areas of the RVEs now differ, the in-plane thickness of the RVEs in each model need to be adjusted accordingly.

Fig. 8

RVEs with similar fibre volume fraction but different widths a 0.125 mm, b 0.25 mm, c 0.5 mm

From the force–displacement plots shown in Fig. 9, the constitutive responses from all three TBeam models with different RVE widths match closely to that of the DNS model. As such, the accuracy of the proposed Direct FE² model is shown to be mostly unaffected by the size of the RVE, suggesting that even the smallest RVE presented is large enough to represent the mesostructure of the heterogeneous material.

Fig. 9

Force–displacement plot of the TBeam models with different RVE widths

4.2 Angle-ply composite beams with single fibre layer lamina

In this second example, we consider two different composite beams constructed from stacking plies with different fibre orientations. The results for these cases will be benchmarked against DNS analyses to investigate the ability of the proposed model in handling more complicated structures and load effects.

4.2.1 Antisymmetric beam with stretch-twist coupling

For Example 2.1, we first consider a beam with an antisymmetric [+ 45/− 45]₂ ply layup subjected to a tensile load. Due to the heterogeneity of the plies, this beam will result in an out-of-plane coupled twisting effect when an axial load is applied. Within the elastic regime, this can be predicted using the Classical Laminate Theory (CLT) [52].

The model is shown in Fig. 10. The RVE of the beam is formed by stacking four plies with their fibres oriented in the respective directions. When viewed along the fibre direction, each ply has a row of eight fibres with a diameter of 0.08 mm and a periodic spacing of 0.1 mm, resulting in a fibre volume fraction of 0.502. The matrix and fibres have the same properties as the previous example, as shown in Table 1. The RVE is modelled with solid brick elements (ABAQUS C3D8) and the DNS model is obtained by tessellating the RVE. For the TBeam model, only one macroscale beam element is used here since this is a homogeneous load. The axial load is then applied by displacing both ends of the beam equally but in opposite directions.

Fig. 10

Antisymmetric beam under axial load a DNS model, b TBeam model, c RVE

As seen from the axial stress–strain plot in Fig. 11, the TBeam model is able to capture the constitutive response of the composite beam very closely, demonstrating its ability to model more complicated structures and loading effects using fewer DOF than a full DNS analysis. The DNS model has a slightly stiffer response when the relative displacements of the ends are used to determine the strain (solid line) due to differences in the boundary conditions of the DNS model and the mesoscale RVEs. In the DNS model, cross-sections at both ends of the beam are displaced uniformly, therefore preventing any perturbations along the axial direction. In contrast, the response of the beam elements in the TBeam model are determined by the homogenized RVEs which permit periodic perturbations and are hence less constrained compared to the DNS model. If the strain in the DNS model is determine from the relative displacements of two points on the centreline 0.565 mm (one RVE length) away from the ends (dashed line), the results from both models match exactly.

Fig. 11

Axial stress–strain plot of the antisymmetric angle-ply beam under axial loading

This is also observed in the Mises stress contours of both models as seen in Fig. 12. Under the homogeneous axial load with a coupled twisting effect, the stress contours of both models match closely. At both ends of the beam, the DNS model is seen to have higher stress values, due to the uniform displacement loads imposed. Furthermore, the deformed configurations of both models also show similar twisting deformations as seen in Fig. 12.

Fig. 12

Mises stress contour (Pa) of the antisymmetric angle-ply beam under axial loading. Displacements perpendicular to the beam axial direction are amplified to show twisting effects more clearly

The angle of twist per unit length in both models are also compared to determine how well the coupled twisting effect is captured by the TBeam model. In the TBeam model, the angle of twist per unit length is simply obtained as the change in ${\varphi }_{1}^{c}$ across the length of the beam. For the DNS model, the in-plane rotations at both end cross-sections are first obtained by considering the in-plane displacements of the nodes. The angle of twist per unit length is then obtained as the difference between them across the length of the beam. As seen in the plot in Fig. 13, there is a clear difference in the values obtained by both models when nodal values at the ends of the beam are used. This is once again due to differences at the loaded ends between solid elements and beam elements. It becomes negligible when the end effects are reduced by using nodal displacements away from the ends of the DNS beam for comparison.

Fig. 13

Plot of angle of twist per unit length against strain for the antisymmetric angle-ply beam under axial loading

4.2.2 Symmetric cantilever beam

For Example 2.2, we consider a beam with a symmetric [+ 45/− 45]s ply layup subjected to a cantilever load as shown in Fig. 14.

Fig. 14

Symmetric beam under cantilever load a DNS model, b TBeam model, c RVE

Except for the RVE ply layup configuration, the TBeam and DNS models are largely identical to that in the previous case. Compared to Example 2.1, the plies in this RVE are rearranged according to the symmetric layup as seen in Fig. 14c. Two macroscale beam elements are now used for the TBeam model instead of one, as the beam deformation varies along its length. Another set of simulations were performed on a beam of length twice that shown in Fig. 14 to investigate end effects. The results from both sets of simulations are plotted on the same diagram in Fig. 15. The bending moment per unit area at the fixed end of the beam is chosen for the ordinate of the plot because nonlinearity due to plastic deformation is caused mainly by bending stresses. To facilitate comparison, the vertical displacement of the free end shown on the abscissa is scaled by the square of the beam length, i.e., ${u}_{3}/{L}^{2}$, to bring all the plots together.

Fig. 15

Moment-displacement plot of cantilever symmetric angle-ply beam

Similar to Example 2.1, the plots show that the TBeam model is able to capture the constitutive response of this composite beam with a symmetric layup using fewer DOF than a full DNS analysis. The results for Example 2.2 (blue plots) also shows that the DNS model has a slightly stiffer response, due to the boundary conditions applied to the two ends of the beam. When the lengths of the beams are doubled, these ends effects are reduced and the moment-displacement plots predicted by both models match more closely, as seen in the red plots.

This is further evidenced by the Mises stress contours of both models with the original length as seen in Fig. 16. At the fixed end of the beam, the DNS model shows slightly higher stresses due to the end conditions. Away from the fixed end, both models predict stress contours that are highly similar. A sectioned view of the DNS model at approximately the same location as the leftmost RVE of the TBeam model also shows a highly similar internal stress distribution in the fibres and matrix.

Fig. 16

Mises stress contour (Pa) of the cantilever symmetric angle-ply beam

4.3 Composite beams with multi-layer fibre lamina

In the previous example, each ply in the RVE had only a single layer of fibres across its height to maintain a practical computational time for the DNS models. Having demonstrated that the proposed TBeam model is able to predict the constitutive response of a given heterogeneous beam with much fewer DOF compared to a full DNS analysis, we reconsider the same angle-ply composite beam but with more fibres per ply that are more representative of actual composites. This makes the model too computationally intensive for a full DNS analysis but the analysis is still manageable with the Direct FE² TBeam model.

When viewed along the fibre direction, each ply now consists of five by ten fibres with a diameter of 0.016 mm as shown in Fig. 17, maintaining the same fibre volume fraction as in previous examples. For each of the beams, four plies are then rotated and stacked to form the respective antisymmetric [+ 45/− 45]₂ and symmetric [+ 45/− 45]_s ply layups.

Fig. 17

Dimensions for one ply in the RVE of beam with multi-layer fibre lamina

The beams still have an overall length of 5.65 mm, now corresponding to a length of 40 RVEs, and are subjected to the same loading conditions used in the previous examples (Fig. 18).

Fig. 18

RVE layup configuration and loading conditions for beams with multi-layer fibre lamina a antisymmetric beam under axial load, b symmetric beam under cantilever load

4.3.1 Antisymmetric beam with axial-twist coupling

The axial stress vs strain plot of the antisymmetric beam is shown in Fig. 19. Compared to the axial stress–strain plot of the beam in Example 2.1, it can be seen that the corresponding stiffness of the beam with smaller fibre sizes is only slightly higher. The plots also show a similar degree of plasticity.

Fig. 19

Axial stress–strain plot of the antisymmetric beam with single- and multi-layer fibre lamina under axial loading

On the other hand, a comparison between the normal stress contours with the RVEs in Examples 2.1 and 3.1 shows clear differences as seen in Fig. 20. The stress contour in the RVE with the smaller fibre sizes (RVE 3.1) shows that the fibres bear larger stresses than that predicted with the RVE with larger fibres (RVE 2.1). While RVE 3.1 shows inter-ply fibre interface stresses that are largely similar to those seen in RVE 2.1, the intra-ply fibre interfaces in RVE 3.1 are shown to have areas with significant compressive stresses, which cannot be observed in RVE 2.1 that has only a single fibre along the height in each ply.

Fig. 20

Normal stress contour (Pa) for the antisymmetric beam with multi-layer fibre lamina under axial load a TBeam model, b magnified view of the left RVE, c corresponding RVE from Example 2.1

4.3.2 Symmetric cantilever beam

From the moment-displacement plot in Fig. 21, it can be seen that this cantilever beam with smaller fibres is significantly more flexible than the beam in Example 2.2. Unlike the stretch-twist coupling example in Fig. 20 where axial strains are uniform over the beam cross section, there is now a strain gradient along the height of the beam. Consequently, the spatial distribution of the heterogeneities strongly affects the beam stiffness. This can be observed from the RVE Mises stress contours in Fig. 22b and c. The RVE with smaller fibres (RVE 3.2) shows significant changes in the fibre stresses along the height of the RVE, even within the same ply. This cannot be captured by the RVE with single large fibres in each ply (RVE 2.2). Moreover, although both RVEs show similar inter-ply fibre interface stresses, once again only RVE 3.2 is able to capture the intra-ply fibre interface stress distributions. Both RVEs also show changes in the stress levels along the direction of the beam axis, with the changes being more obvious in RVE 3.2.

Fig. 21

Moment-displacement plot of the symmetric beam with multi-layer fibre lamina under cantilever load

Fig. 22

Mises stress contour (Pa) for the symmetric beam with multi-layer fibre lamina under cantilever load a TBeam model, b magnified view of the leftmost RVE, c corresponding RVE from Example 2.2

Both these examples underscore the importance of modelling heterogeneous structures with sufficient details to obtain more accurate predictions from FE analyses. Hence, the proposed TBeam model may prove useful in circumstances whereby detailed predictions are required but a full DNS analysis remains unfeasible due to computational limits, and the problem cannot be simply reduced to an RVE analysis as in the case for homogeneous loads. Beyond composites, the model can also be similarly applied to beam problems involving other types of heterogeneous structures, as long as the base material properties are known and an appropriate RVE can be constructed.

5 Conclusions

A Direct FE² homogenisation model for a beam element that takes into account transverse shear deformations based on the Timoshenko-Ehrenfest beam theory has been presented. It is shown that the multiscale analysis can be carried out as a single FE analysis on commercial codes and is easily implemented through two pre-processing steps—setting up multipoint constraint equations to link macroscale and mesoscale degrees of freedom and scaling the volume of the mesoscale RVE mesh for energy consistency. The kinematic downscaling of the shear angle is key to the development of such a framework and is achieved by equating the moments of axial displacement about the centroid of the beam cross section at both macro- and meso- scales. Examples in 2D and 3D demonstrate the proposed model accurately reproduces predictions from DNS. Plots of beam displacements vs load agree to within 2%. The coupling of axial stretching and twisting in antisymmetric fibre reinforced composite beams was also captured correctly. Besides similarity in structural response, stress contours within the DNS model and the RVEs of the FE² model also matched closely. Because of the reduction in degrees of freedom, large savings in computational cost over DNS are achieved. For the 2D example shown, the proposed FE² model gave results similar to the DNS model but took only 13% of the computational time. Direct FE² homogenization was also implemented based on the kinematics of Euler beam theory. With no provision for shear deformation, the model was significantly stiffer compared to the DNS model and homogenized Timoshenko-Ehrenfest beam for shear dominant loads. This further shows that the proposed model is an important addition to the repertoire of homogenisation models developed.

Appendix A: Imposition of an integral constraint for shear

In this appendix, the thought process leading up to the integral constraint Eq. (32) will be presented. As previously discussed in Sect. 3.3, the constraints arising from first-order homogenisation alone are insufficient to constrain the RVE and would result in spurious rotations. To illustrate this, we consider a RVE located at an integration point of a homogeneous beam subjected to simple shear, i.e.,

$${\varphi }_{2}^{c}=\nabla {\varphi }_{2}^{c}=\nabla {u}_{1}^{c}=0,\nabla {u}_{3}^{c}>0$$

(41)

For a homogeneous beam, the RVE is expected to deform as shown in Fig. 23a to match the macroscale kinematics described above. However, the constraints presented in Sect. 3.1 would result in the RVE undergoing a rotation about the 2-axis as shown in Fig. 23b. It is pointed out that this is not strictly a rigid body rotation as the RVE is stretched in the beam’s axial direction to satisfy the macroscale constraint $\nabla {u}_{1}^{c}=0$. A comparison with Fig. 23a shows that the shear angle, ${\varphi }_{2}^{c}$, is not being imposed onto the RVE in Fig. 23b. This is because the shear angle does not appear in any of the constraint equations in Sect. 3.1. We present several attempts to address this.

A natural first consideration would be to constrain ${\widehat{u}}_{1}$ such that it matches ${u}_{1}$ in an average sense over the height of the beam, i.e.,

$$\int {\widehat{u}}_{1}d{\widehat{x}}_{3}=\int {u}_{1}d{\widehat{x}}_{3}$$

(42)

For the simple shear described by Eq. (41), this is simply,

$$\int {\widehat{u}}_{1}d{\widehat{x}}_{3}=0$$

(43)

Due to the periodicity of ${\widehat{u}}_{1}$ from Eq. (14), such a constraint needs to be imposed on only one boundary of the RVE, either left or right. However, imposing this constraint still resulted in the rotation as seen in Fig. 23b.

Next, we attempt to impose ${\widehat{\varphi }}_{2}$ to match ${\varphi }_{2}$ in an average sense over the height of the beam instead, i.e.,

$$\frac{1}{{h}_{RVE}}\int {\widehat{\varphi }}_{2}d{\widehat{x}}_{3}={\varphi }_{2}^{c}$$

(44)

Note that ${\varphi }_{2}$ is a DOF only in the macroscale beam element but not the ${C}_{0}$ solid elements used to model the RVE. As such, a proxy is used for ${\widehat{\varphi }}_{2}$ instead.

$${\widehat{\varphi }}_{2}=-\frac{\partial {\widehat{u}}_{1}}{\partial {\widehat{x}}_{3}}$$

(45)

Substituting the Eq. (45) into Eq. (44) and performing the integration yields the constraint

$${\widehat{u}}_{1}^{B}-{\widehat{u}}_{1}^{T}={h}_{RVE}{\varphi }_{2}^{c}$$

(46)

where ${\left(\cdot \right)}^{B}$ and ${\left(\cdot \right)}^{T}$ refer to the bottom and top node of the RVE boundary respectively. Imposing this constraint would result in the deformed RVE as shown in Fig. 23c. The RVE is seen to undergo a rotation that is constrained at the four vertices, which is clearly incorrect.

The constraint in Eq. (43) is then revisited to understand why it fails to enforce the correct shear angle ${\varphi }_{2}^{c}$ onto the RVE and prevent the spurious rotations. From Fig. 23b, it can be seen that the spurious rotation causes ${\widehat{u}}_{1}$ of the RVE boundary to deviate from ${u}_{1}$ by a similar magnitude but in opposite directions above and below the neutral axis, ${\widehat{x}}_{3}=0$. As a result, ${\widehat{u}}_{1}$ and ${u}_{1}$ still match in an average sense despite significant local deviations.

Instead of imposing ${\widehat{u}}_{1}$ to match ${u}_{1}$, we then attempt to match the moments of ${\widehat{u}}_{1}$ and ${u}_{1}$ about the centroidal axis in an average sense, i.e.,

$$\int {\widehat{x}}_{3}{\widehat{u}}_{1}d{\widehat{x}}_{3}=\int {\widehat{x}}_{3}{u}_{1}d{\widehat{x}}_{3}$$

(47)

Using Eq. (1) for the macroscale axial displacement and performing the integration on the RHS, we then obtain the constraint

$$\int {\widehat{x}}_{3}{\widehat{u}}_{1}d{\widehat{x}}_{3}=-\frac{{\left({h}_{RVE}\right)}^{3}}{12}{\varphi }_{2}^{c}$$

(48)

Imposing the constraint in Eq. (32) onto the RVE results in the deformation as seen in Fig. 23d—a close match to the expected deformation.

Fig. 23

RVE deformations with different shear angle constraints

Fig. 24

Shear strain contour plot for RVE with displacement moment constraint

Furthermore, the shear strain contour of the RVE in Fig. 24 shows that the transverse shear is low at the top and bottom surfaces of the RVE and peaks towards the mid-height, consistent with the theoretical description of transverse shear in beams.

Fig. 25

Shear stress (Pa) contours of beams under shear a solid elements model, b direct FE² model with the shear angle kinematic integral constraint

Although the transverse shear is not exactly zero at the top and bottom surfaces, this is an expected effect from the finite element discretisation. This can be seen from a simple comparison between solid elements and the proposed Timoshenko Beam Direct FE² model using a homogeneous beam subjected to a transverse shear load. As seen in Fig. 25, the beam modelled using solid elements also shows low but nonzero transverse shear stresses at the top and bottom surfaces, and the shear stress contour from the Direct FE² model matches closely to that from the former.