Blind Rendezvous for Multi-users Multihop System

Abstract

In the previous chapters of Part II, we introduce rendezvous algorithms between two users of different settings. As we know, typical distributed systems have a large number of entities, and two users wanting to communicate may not be able to that directly. Therefore, we extend the blind rendezvous algorithms between two users to multiple users in a multi-hop system in this chapter. Actually, the idea for the extension is not hard to follow. We take the Disjoint Relaxed Difference Set (DRDS) based rendezvous algorithm (please refer to Chap. 8) as an example. As described in Problem 5.2, the system consists of M users with available set $C_i$ for user $u_i$ and the common available port set $G = \bigcap \nolimits _{i=1}^m C_i \ne \emptyset$. Suppose the diameter of the system is D, which implies any two users are connected within D hops. Notice that, if the system is not a connected component, no information can be exchanged between any disconnected components, and each separated disconnected component could run the rendezvous algorithm independently and the result would not affect the other components. We propose a distributed blind rendezvous algorithm that guarantees rendezvous for all users in $O(N^2 D)$ time slots in Sect. 10.1. The correctness and time complexity are derived in Sect. 10.2. We discuss about the rendezvous problem in a general multi-hop system in Sect. 10.3 and we summary the chapter in Sect. 10.4.

1 Algorithm Description

We adopt the intuitive idea in [1,2,3] to extend the DRDS algorithm for Problem 5.1 to the multiple users version: once every two users rendezvous on some common available port successfully, they can exchange the information about the set of available ports and they can synchronize their parameters (the set of available ports) such that they would generate the same hopping sequence afterwards.

Assume the available port set to be $C\subseteq U$, and we describe the algorithm as in Algorithm 10.1. The user runs the DRDS based rendezvous algorithm based on its own port set C. Once rendezvous happens with another user who has available port set $C' \subseteq U$, they can exchange their information about the available ports and update $C = C \bigcap C'$, and then continue the rendezvous process. It is easy to see that two users would generate the same hopping sequence until another rendezvous happens. The correctness and time complexity are analyzed in Theorem 10.1.

2 Correctness and Complexity

Theorem 10.1

Algorithm 10.1 guarantees that all users can achieve rendezvous in $MTTR = O(N^2 D)$ time slots, where D is the diameter of the network.

Proof

The theorem can be proved as follows. Since every two users $u_i,u_j$ are connected within D hops, denote all the users along the shortest path connecting two users as:

$$\begin{aligned} \{u_{l_0},u_{l_1},u_{l_2},\ldots ,u_{l_k}\} \end{aligned}$$

(10.1)

where $k \le D, u_{l_0} = u_i, u_{l_k} = u_j$. We show that user $u_{l_h}$ can update the set of available ports (denoted as $C_{l_h}'$) as a subset of $C_i\bigcap C_{l_h}$ in $O(N^2 h)$ time slots.

We apply the inductive method on $l_h$ where $0\le h\le k$:

• (1) When $h=0$, $u_i = u_{l_0}$ and thus the theorem holds;

• (2) suppose when $h\le h'<k$, user $u_{l_h}$ can update the set of available ports as:

  $$\begin{aligned} C_{l_h}' \subseteq C_i \bigcap C_{l_h} \end{aligned}$$

  (10.2)

  in $O(N^2 h)$ time slots. Since user $u_{l_{h'+1}}$ can rendezvous with user $u_{l_h'}$ in $O(N^2)$ time slots and they would update (synchronize) their sets of available ports, thus we have:

  $$\begin{aligned} C_{l_{h'+1}}' = C_{l_h}' \bigcap C_{l_{h'+1}} \subseteq C_i \bigcap C_{l_{h'+1}} \end{aligned}$$

  (10.3)

  and the time is bounded by $O(N^2(h+1))$.

Combining the two cases, $u_j$ can update the set of available ports as $C_j' \subseteq C_i \bigcap C_j$ in $O(N^2 D)$ time slots. Therefore, for any user $u_j$ and any other user $u_i$ in the network, the synchronized port set would be $C_j' \subseteq C_j \bigcap C_i$ after $O(N^2 D)$ time slots. Thus, the final available port set for user $u_j$ should be $\bigcap _{i=1}^m C_i$ if all users have begun the rendezvous process for $O(N^2 D)$ time slots. Thus, all users hop through the available ports according to the same sequence generated by the DRDS based rendezvous algorithm. The theorem holds.

3 Discussions

In practice, the rendezvous process among multiple users in a multihop system could be more complicated. In this book, we make the assumption as in [3] that all users in the system share at least one common channel (the assumption is to suit cognitive radio networks, but should also apply to many distributed systems). This assumption is meaningful in some specific applications, such as file sharing where the system would dedicate a common external port, and message broadcasting which must be conducted on a common channel. A system is fully connected for communication if every two neighboring users share some common available port, which does not have be made known to all users.

Fig. 10.1

An example of rendezvous among multiple users in a multihop CRN

Considering a Cognitive radio network where five SUs coexist with four PUs as depicted in Fig. 3.3 and they share the common available channel 5. When PU4 occupies channel 5, rendezvous between every pair of neighboring users can still happen. As illustrated in Fig. 10.1, (secondary) user A can rendezvous with user B on channel 5, user B can rendezvous with user C on channel 3, 4 or 5, user B can rendezvous with user D on channel 4 when channel 5 becomes unavailable for user D, and user D can rendezvous with user E on channel 1, 4 or 6. Although the five users do not share a single common available channel, rendezvous can happen between every pair of neighboring users, and thus the rendezvous process to cover the entire network can still be fulfilled.

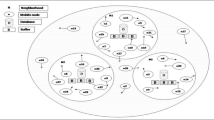
This mode of communication takes place in many distributed systems, when the external ports are occupied by some unpredicted services or events. For example, in Fig. 10.2, node a can be connected to three neighbors and they have different sets of available ports. Node a and node b can achieve rendezvous on common port 4 or 6, node a and node d can rendezvous on common port 1 or 6, while node a and node c can only rendezvous on common port 2. Although there exists no common port among the four nodes, they can construct communication link between every pair of neighbors. If node b wants to send a message to node c, it can first send the message to node a through port 4 or 6; after receiving the message, node a can re-transmit it to node c through port 2. Therefore, communication over the entire system is maintained. Therefore, we aim to design efficient algorithms to construct a distributed system based on the rendezvous process between every pair of neighboring users in the future.

Fig. 10.2

An example of rendezvous among multiple entities in a distributed system

4 Chapter Summary

In this chapter, we study the blind rendezvous problem for multiple users in a multi-hop distributed system. The intuitive idea is to generate the rendezvous sequence according to different local parameters. For example, according to the users’ identifier (ID) and the available ports set, the user can establish a fixed rendezvous sequence. For every two neighboring nodes in the system, if they rendezvous on some common available port, they can synchronize their local parameters and then they can access the ports by the same rendezvous sequence. This extension could help solve the rendezvous problem in a multi-hop distributed system and they can finally compute the common available port among all the users. This can be useful in some applications, such as one node tries to broadcast a message to all nodes through a common available port.

In many practical applications, there may not exist a common available port among all users but they can construct communication link between every two neighboring users. Therefore, it is a practical and good topic to design efficient rendezvous algorithms for a pair of neighboring users with short rendezvous time.