Keywords

1 Introduction

Earthquake phenomenon is not new in India and tremors of earthquake from nearby countries are often felt which causes threats to public safety and damage to property. Based on geometric location quiet near to the seismic fault line of Himalayan range, any structure has chances to fail especially high rise buildings. Damage induced due to earthquake has increased over the last few years and some devastating examples are from Gujarat earthquake in 2001, Nepal earthquake in 2015 and earthquake in Sumatra in 2004 which left India and other South Asian countries shocked. Collapse of engineered and non-engineered structure is the major contributor in loss to human life.

Over the past few decades progress has been made in making the structural control system such as vibration control a practicable technology for improving structure functionality and safety against natural hazards like earthquakes.

The effectiveness of the Tuned Mass Damper (TMD) depends on the right standardization of the characteristics of TMD in a structure. Hybrid Self Organizing Migrating Algorithm is used to optimize the TMD so that structural response can be improved.

Frahm [2] in 1909 was the first to work and implement the concept of a Tuned Mass Damper (TMD), to reduce vibrations and motion in ships. Later Den Hartog [3] developed theory for a single degree of freedom system. A detailed discussion about optimal parameters of Tuned Mass Damper was provided by them later in 1940. Sadek et al. [4] suggested that TMD performs efficiently when first two modal damping modes are equal, as earlier formulations by other authors don’t show the equality in the damping of the first two modes. Bekdaş and Nigdeli [1] optimized the damper properties using metaheuristic technique known as Harmony search.

2 Simplification of a Structure to a SDOF System

A structure is actually not a single degree, but rather it is an infinite degree of freedom system. It is however, mathematically impossible to simplify the structure’s model, an approximation requires to use the lumped mass model, where the model goes from an infinite to a multiple (finite) degree of freedom system. This is achieved by considering each floor as a Single Degree of Freedom (SDOF), where the mass is the total mass of the considered floor, and the stiffness and damping are calculated using equivalence formulas - which depend on the properties of elements (E, l, C), the fixations at the end.

Equation of motion for a Multi Degree of Freedom (MDOF) system is given by

$$ [m]\{ \ddot{x} (t)\} + [c]\{ \dot{x} (t)\} + [k]\{ x(t)\} = [m]\{ r\} \ddot{x}_{g} (t) $$
(1)

Where m, c, k are mass matrix, damping matrix and stiffness matrix and {r} is influence coefficient vector (nX1) with \( \ddot{x}\left( t \right) \) denoting relative acceleration vector \( \dot{x}\left( t \right) \) relative velocity vector and \( x\left( t \right) \) relative displacement vector, \( \ddot{x}_{g(t)} = \) EQ ground acceleration or excitation.

The undamped eigen values and eigen vectors of MDOF are found for the characteristic equation for n stories by:

$$ \begin{aligned} \left\{ {k - \omega_{i}^{2} \left[ m \right]} \right\}\emptyset_{i} = 0; \hfill \\ { \det }|\left\{ {k - \omega_{i}^{2} \left[ m \right]} \right\}| = 0; \hfill \\ \end{aligned} $$

Where; i = 1 to n where n is total number of stories.

Where displacement response of MDOF is expressed as \( {\text{x}}\left( {\text{t}} \right) = [\emptyset ]\left\{ {{\text{y}}\left( {\text{t}} \right)} \right\}; \)

Where y(t) represent modal displacement vector and [\( \emptyset \)] is the mode shape matrix given by [\( \emptyset \)] = [\( \emptyset_{1} \emptyset_{2} \emptyset_{3} \emptyset_{4} \) . . . . \( \emptyset_{n} \)].

Substituting \( \{ x\} = [\emptyset ]\{ \text{y}\} \) in Eq. 1 and pre multiplying by transpose of \( [ \emptyset ] \) i.e. \( [\emptyset ]^{T} \)

$$ \begin{aligned} \left[ \emptyset \right]^{T} \left[ m \right][ \emptyset ] \{ \ddot{y}\left( t \right)\} & + [\emptyset ]^{T} \left[ c \right][ \emptyset ] \{ \dot{y}\left( t \right)\} + [\emptyset ]^{T} \left[ k \right][ \emptyset ] \{ y\left( t \right)\} \\ & = [\emptyset ]^{T} \left[ m \right]\{ r\} \ddot{x}_{g} (t) \\ \end{aligned} $$

  • \( [\emptyset ]^{T} [\text{m}][\emptyset ] = [\text{M}] \); Generalized mass matrix

  • \( [\emptyset ]^{T} [\text{c}][\emptyset ] = [\text{C}] \); Generalized damping matrix

  • \( [\emptyset]^{T} [\text{k}][\emptyset] = [\text{K}] \); Generalized stiffness matrix

and equation becomes

$$ \ddot{y}_{i} \left( t \right) + 2\varepsilon_{i} \omega_{i} \dot{y}_{i} \left( t \right) + \omega_{i}^{2} y_{i} \left( t \right) = \tau_{i} \ddot{x}_{g} (t) $$
(2)

Where; \( y_{i} \left( t \right) \) = modal displacement response in \( i^{th} \) mode

  • \( \varepsilon_{i} \) = modal damping ratio in \( i^{th} \) mode

  • \( \tau_{i} \) = modal participation factor for \( i^{th} \) mode expressed by

$$ \tau_{i} = ([\emptyset ]^{T} \left[ m \right]\{ r\} \ddot{x}_{g} )\,/\,([\emptyset ]^{T} \left[ m \right][\emptyset ]) $$

Equation (2) can also be written as

$$ m\ddot{x}\left( t \right) + c\dot{x}\left( t \right) + kx\left( t \right) = - m\ddot{x}_{g} (t) $$

Where; \( \omega_{^\circ } = \sqrt k /m \) and \( \varepsilon = c/(2m\omega_{^\circ } ) \)

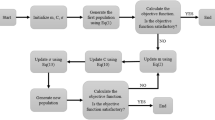
2.1 Optimization Procedure

The primary objective of optimization is to reduce the vibration of structure subjected to seismic loading under different earthquake excitations recorded in the past. The fundamental parameter considered is the maximum displacement of the structure. To increase the effectiveness of the TMD, the following parameters are optimized: Mass ratio (μ) i.e., ratio of mass of TMD (md) to the mass of the structure (M)• Stiffness of the Tuned Mass Damper (kd)• Damping coefficient of the TMD (cd)• The methodology aims at optimizing the parameters for the first mode of vibration of the structure. In order to optimize the parameters of TMD, the structure was idealized as lumped spring–mass-damper single degree of freedom system (SDOF). The mass of the SDOF was considered as the modal mass participated in the first mode of the structure. The TMD was attached to the structure as spring-mass-damper system and the SDOF structure becomes 2DOF system. The parameters of the TMD are found as follows,

  • Mass of TMD (md)

    • md = μ M

  • Stiffness of TMD (kd)

    • kd = ωo 2 * α * 2 m

  • Damping of the TMD (cd)

    • \( c_{\text{d}} = 2\,\text{m}\,\varepsilon_{\text{d}} \,\omega_{d} \)

The equation of motion of system equipped with a TMD is given in Eq. 3, where the parameters \( m_{d} ,\,c_{d} ,\,k_{d} \) were optimized by setting the range of the TMD parameters of the structure and then finding the best optimum solution of TMD parameters with the help of SOMGA and SOMAQI.

$$ \left( {m + m_{d} } \right)\ddot{u} + \text{c}\ddot{u} + {\text{ k u + }}m_{d} \,\ddot{u}_{d} + \text{c}_{d} \,\dot{u}_{d} + k_{d\,} u_{d} = \text{p} $$
(3)

Where;

  • m = mass of the structure alone

    • c = damping of the structure

    • k = stiffness of the building alone

    • \( m_{d} = \) mass of damper

    • \( c_{d} = \) damping of the tuned mass damper

    • \( k_{d} = \) stiffness of the damper

    • p = loading applied on the building

    • u = displacement of primary mass

    • \( u_{d} = \) displacement of damper

The range is as follows:

$$ \begin{array}{*{20}l} {m_{d} = 13850 \,to\, 69250} \hfill \\ {k_{d} = 1.3375 \times 10^{5} \,to\, 6.68759 \times 10^{5} } \hfill \\ {c_{d} = 8.608 \times 10^{3} \,to \,43.04 \times 10^{3} } \hfill \\ \end{array} $$

3 Case Studies

Two examples from the existing literature are selected and the use of Hybrid SOMA method is applied on them for finding the optimum TMD parameters for them.

3.1 Case Study-1

Case Study 1 is on example taken from Singh et al. [5] in which all floors have the same properties i.e. same mass, stiffness and damping coefficient as 360t, 650 MN/m, and 6.2 MNs/m for all the ten floors. After performing the analyses for optimization, optimum TMD parameters are found as md = 70.312t, cd = 93.6 kNs/m and kd = 2973.34 kN/m using SOMGA Technique and from SOMAQI technique parameters are found as md = 180 t, cd = 46.8 kNs/m and kd = 7612.02 kN/m. These values for TMD parameters are smaller than the values obtained by previous studies and this example was analyzed under El Centro NS (1940) excitation for comparison with previous results. The maximum displacement response obtained for first story, top story and TMD under different earthquakes are presented in Table 1 and for the comparison, response of all the stories under El Centro NS (1940) with displacement responses from previous studies are presented in Table 2.

Table 1. Maximum displacements respect to ground under different earthquakes for Case Study-1
Full size table
Table 2. Maximum displacements respect to ground under EL Centro NS excitation for Case Study-1
Full size table

Table 2 shows the maximum displacement response reduction for the structure stories in terms of percentage for the present study which are written against the values of optimized result from the past studies of Harmony search and Genetic algorithm optimization. From the study, it is found that the maximum top floor displacement of the building is reduced by 52.13% under EL Centro NS (1940) excitation with SOMGA and 39.89% by SOMAQI, whereas GA showed 35.11% reduction and Harmony Search algorithm showed reduction of 45.74%.

3.2 Case Study-2

The second example in Case Study 2 is also a ten story building which was optimized before by Sadek et al. [4] and the structure has different values of parameters for all floors as seen in Table 3 below.

Table 3. Structure properties of Case Study 2
Full size table

In this study the damping matrix is taken proportional to the stiffness matrix i.e. C = 0.0129 K for the second example as it was given in the paper that it can be taken proportional to the stiffness matrix or the mass matrix. Optimum TMD parameters for the Case Study-2 are found as md = 20.789 t, cd = 17.25 kNs/m and kd = 198.536 kN/m using SOMGA Technique and TMD parameters from SOMAQI are found as md = 69.25 t, cd = 43.04 kNs/m and kd = 668.759 kN/m. The maximum displacement response obtained for first story, top story and TMD under different earthquakes are presented in Table 4 and for the comparison, response of all the stories under El Centro NS (1940) with displacement responses from previous studies are presented in Table 5.

Table 4. Maximum displacements respect to ground under different earthquakes for Case Study-2
Full size table
Table 5. Maximum displacements respect to ground under EL Centro NS excitation for Case Study-2
Full size table

From Tables 4 and 5 it can be seen that both the soft computing techniques which are used for optimization of the TMD parameters are working fine, as for the values of TMD parameters, significant reduction in maximum absolute displacement of the structure storey can be seen for Example 2 under different earthquake records. The values of displacement obtained from the present study are better than the values obtained from previous studies. While the results obtained from the TMD parameters derived from SOMGA are performing in a better way as compared to the results obtained from SOMAQI.

It is found that the maximum displacement of the top story is reduced by a reduction of 53.82% by SOMGA and 37.31% by SOMAQI under El Centro NS (1940) excitation, while the top story displacement is reduced with a reduction of 15.6% by Den Hartog 14.07% by Sadek et al. and 37.31% by Gebrail-Sinan Harmony Search method and 16.82% by Hadi-Arfiadi methods. TMD parameters obtained by SOMGA are numerically smaller than various other methods which were compared and efficient in reducing the displacement response, while the parameters obtained by SOMAQI are similar to the parameters obtained by other studies in reducing the maximum absolute response of the structure with respect to the ground under different earthquake excitations.

4 Conclusions

In this paper two case studies have been considered for analysis. In case study 1, all the floors have the same properties i.e. same mass, stiffness and damping coefficient for all the ten floors and in Case study 2, different values of mass, stiffness and damping coefficient has been taken for all floors. In both cases, the parameter of TMD has been optimized by two soft computing techniques. Both the techniques are performing better as the displacement is reduced as compared to previously published results. Results showed that among these two techniques, SOMGA is showing better reduction of displacement of the top and bottom storey as compared to SOMAQI. Hence it can be concluded that displacement responses can be achieved for any structure incorporated with TMD with the help of Hybrid Self Organizing Migration Algorithm.