A Novel Flexible Experiment Design Method

Abstract

Latin Hypercube Design (LHD) is a traditional method of Design Of Experiments (DOE) and is often employed in system analysis. However, this method imposes restriction on experiment trials and needs much computation capacity to obtain the optimal design. A novel experiment design method called ETPLHD is proposed in this paper to solve this problem. ETPLHD can control the number of design points and thus presents more flexibility to control the number of experiment trails, which is more efficient compared to the fixed experiment trails in the traditional LHD method for a same design space. An experiment was conducted to compare ETPLHD with the other two experiment design algorithms. The results showed that TPLHD reveals high design performance and less time consumption.

1 Introduction

Simulation is a promising way to study the complex systems with high performance-price ratio [1]. To analysis the characteristics of the target system, normally a large number of experiment trails need to be run and different level combinations of the parameters are tested. While the high-performance computation facilities are widely used to speed up the computation, the computation capacity required in system analysis still makes it difficult to test each level combination of all parameters, especial for those complex systems with large set of parameters. Even a simple application with 5 parameters, and each parameter contains 10 levels, $10^{6}$ min (over 2 years) is required to test all level combinations assuming each trail need 10 min to run.

As a result, the DOE technique is widely used in any experiment-based domains [2] for its capability to analyze the target system with less experiment trials. The DOE method normally selects a small amount of typical experiment points in the parameter space, to obtain the comprehensive understanding of the target system. It is not necessary to test each level combination of the parameters, thus improving the experiment efficiency greatly. The model of the target system is expected to be derived based on this small amount of experiments, then the further analysis even the prediction can be made.

A critical property is the space-filling property, i.e., how the design points distributed in the experiment space. Among various DOE methods, the Latin Hypercube Design (LHD), which was proposed by McKay [3], is most used in simulations [4]. It is always the concern in different variants of LHD design to obtain better space-filling property. Park developed a row-wise element exchange algorithm to obtain the optimal LHD [5]. Morris and Mitchell applied simulated annealing algorithm to optimize the design [6]. Bates et al. employed the Genetic algorithm to optimize LHD [7]. Although these variants present good performance, the involved number of experiment trails is large. Felipe Viana et al. proposed a fast optimal Latin Hypercube Design using Translational Propagation algorithm (TPLHD) [8]. TPLHD generates nearly optimal design instead of the global optimal design. However, the number of experiment trials of TPLHD is fixed for discrete experiment space, which is often insufficient to fully explore the experiment space.

In this paper, an Extended TPLHD method (ETPLHD) is proposed to generate the design points flexibly. ETPLHD can generate more points in the design space than traditional LHDs, which will be helpful in study of the target system. It was shown in the comparison with other DOE methods that ETPLHD is efficient to produce the experiment points, and achieved better evaluation results about the studied system.

The rest of this paper is organized as follows. Section 2 gives a brief introduction of TPLHD. Then the proposed method ETPLHD is described in detail. Section 3 introduces the linear regression model for system approximation and predication. Section 3.2 presents the comparative experiment between ETPLHD and the other two DOE methods, and the results analysis is given. Finally, the remarkable features about ETPLHD approach is concluded in Sect. 4.

2 Method

2.1 Review of Latin Hypercube via Translational Propagation (TPLHD)

TPLHD method works in real time at the cost of finding the near optimal design instead of the globally optimal design. Suppose a design space with n$_v$ variables, each variable has n$_p$ levels. The first step in TPLHD is to create a seed design that contains n$_s$ points. This seed design is used as a pattern to fill the experiment space iteratively. To fill the space, the experiment space is partitioned into n$_b$ blocks firstly:

$$\begin{aligned} {n_b=n_p/n_s} \end{aligned}$$

(1)

The number of levels contained by each block is determined as follows:

$$\begin{aligned} {n_d=(n_b)^{1/n_v}} \end{aligned}$$

(2)

The second step is to fill the seed design into each block. An example is illustrated in Fig. 1. A seed design containing only 1 point is created in a $9\times 2$ (two variables and each has 9 levels) design space. Then the original space is divided into $9/1 =9$ blocks, and each block has $9^{1/2}=3$ levels. As Fig. 1(a) shows, the seed design is placed in the left-bottom block firstly. Then the seed design is iteratively shifted by $n_p/n_d=3$ levels along one dimension until this dimension is filled with the seed design, as Fig. 1(b) and (c) shows. Next, the design along this dimension is adopted as a new seed design to fill along other dimension until all blocks are filled, as shown in Fig. 1(d).

Fig. 1.

The procedure of creating $9\times 2$ TPLHD

As all the key operations are to translate the design points, The TPLHD method requires much less computation compared to other optimal methods which normally need to search the best design among all $(n_p!)^{n_v}$ LHD designs.

A criterion parameter $\phi _p$, is used to measure the space-filling quality of the experiment design. For an experiment space, a smaller $\phi _p$ indicates that the created experiment points are better in distribution to fill up the space.

$$\begin{aligned} {\phi _p=[\sum _{i=1}^{{n_p}-1}\sum _{j=i+1}^{n_p} d_{ij}^{-p}]^{1/p}} \end{aligned}$$

(3)

where p is a pre-selected integer value and $d_{ij}$ is the distance between any two design points $x _i,x _j$:

$$\begin{aligned} {d_{ij}=d(x _i,x _j)=[\sum _{k=1}^{n_v} |x _{ik}-x _{jk}|^t]^{1/t}} \end{aligned}$$

(4)

$\phi _p$ is also adopted in this paper to measure the space-filling quality of experiment design. As suggested by Jin et al. [9], the value $p=50, t=1$ is taken here. TPLHD method works well with experiment design less than 6 variables. It is difficult to approximate a good experiment design in high-dimensional space for 2 reasons: (i) the Curse of Dimensionality. The partitioned blocks in experiment space will grow exponentially with dimensions; (ii) the distribution of experiment points will be asymmetry in high-dimensional space with linear partition.

2.2 The Extented TPLHD (ETPLHD)

The number of experiment points in TPLHD is constrained by $n_p$, which is the levels of the variable. This characteristic will lead to a small point set most of the time. For example, a size of $10\times 5$ experiment design space contains total $5^10$ level combinations, however, only 10 experiment points would be chosen with TPLHD method. Obviously, this small amount of experiments is insufficient to analysis the target system.

To increase the experiment points, the ETPLHD s proposed in this paper to provide a layered design approach to obtain better distribution of the experiment points. The horizontal interpolation is employed in ETPLHD to design the experiment in an expanded space and then is scaled into the origin space.

Assuming all variables having the same number of levels, Eq. (2) is modified as:

$$\begin{aligned} {d=n_p^{1/2}} \end{aligned}$$

(5)

d is expected to be an integer value, thus $n_p$ needs to be rounded as the value that can be squared such as 4, 9 or 16. For instance, $n_p=15$ can be rounded up to 16, i.e. one extra level is added into the experiment space, then the points corresponding to the extra level are eliminated at last to correct the design.

ETPLHD holds that each block contains the same number of points as TPLHD. However, the number of blocks in ETPLHD is much bigger than that in TPLHD for cases with more than two dimensions, leading to the increment of the design points in ETPLHD (denoted as $n^*$).

$$\begin{aligned} {n^*=d^{n_v}=n_p^{{n_v}/2}} \end{aligned}$$

(6)

Consider a $n \times m$ (n levels, m variables) experiment space. Initially, one dimension (variable) is chosen to be divided into intervals according to Eq. (5). After this operation, the experiment design is conducted in a subspace $n\times (m-1)$ within each block, where the dimension that has been divided is excluded. The design in subspace $n\times (m-1)$ takes the same steps:chose one dimension to divide, and then perform the experiment design in a lower dimensional subspace, until the TPLHD method is applied.

Figure 2 illustrates this process taking a design in $16\times 3$ experiment space. First, one dimension (denoted as the $1^d$) of the experiment space is chosen and partitioned into 4 parts according to Eq. (5). 4 intervals along this dimension are determined, as shown in Fig. 2(a). Next, a $16\times 2$ TPLHD designs (the dimensions are denoted as $2^d$ and $3^d$) is conducted in each interval. By this way, the ETPLHD generates 64 points. For comparison, TPLHD obtains a design with 16 points.

Fig. 2.

The procedure to create $16\times 3$ ETPLHD

In this example, the experiment points within low-dimensional subspace need to be expanded to the higher dimension. Generally, if the points set $x _{im}$ has been obtained within a subspace of m dimensions, the design points can be expanded to the higher dimension as follows:

$$\begin{aligned} {x _{i(m+1)}^k=x _{im}mod\; \textit{d}+(k -1)\cdot \textit{d}} \end{aligned}$$

(7)

where $k(1 \le k \le d_{m+1})$ is the index of the interval along dimension $m +1$. The expansion is repeated until all dimensions are included. As for the example in Fig. 2, the experiment points form the slanted layer along the dimension $1^d$, as shown in Fig. 2(c).

After the expansion to higher dimension, some points may stay in a small region of the experiment space. Consider the example in Fig. 2, an experiment point $[x_0,y_0]$ designed in the $2^d \times 3^d$ subspace will generates a series experiment points along dimension $1^d$ by taking the expansion operation: $[x_0,y_0,z_0], [x_0,y_0,z_3], [x_0,y_0,z_7], [x_0,y_0,z_{11}]$. From the direction of the dimension $1^d$, they are lines. This problem will be worse when the dimension grows.

As a result, it is necessary to adjust the distribution of the experiment points before expansion to the higher dimension. Assuming the current dimension is m, then the points are shifted $p(0\le p\le d_m)$ unit along the $2\sim m$ dimension, where $d_m$ is the number of the intervals along dimension m. Equation (7) is changed as follows:

$$\begin{aligned} {x _{i(m+1)}^k=(x _{im}+p)mod\; \textit{d}+(k -1)\cdot \textit{d}} \end{aligned}$$

(8)

There are two issues should be noted. First, the value of p is normally determined empirically. Second, a control parameter s can be defined to specify how many dimensions need to apply the ETPLHD method. For a $n\times m$ space, $s=2$ means only two dimensions apply the ETPLHD method and the rest $m-2$ dimensions will apply the TPLHD method. By the control parameters, the number of experiment points determined by ETPLHD is:

$$\begin{aligned} {n^*=n_p\cdot d^s=n_p^{\frac{s}{2}+1}} \end{aligned}$$

(9)

Figure 3 demonstrates the shift within the $2^d\times 3^d$ subspace before expansion to dimension $1^d$.

Fig. 3.

Translate the seed on each layer

The pseudo code of ETPLHD is shown as follows:

Algorithm 1: ArrayCreateETPLHD(m, n, s)

2.3 DOE Methods Comparison

Three DOE methods, ETPLHD, TPLHD and a random-selection based LHD method lhsdesign (the implemented function name in Matlab) are compared to demonstrate the effectiveness of ETPLHD. The lhsdesign method selects the LHD according to the best max-min criterion, i.e., the maximization of the minimum distance $d_{min}$, from 200 random LHDs. $d_{min}$ is the other measure of the points density (similar with $\phi _p$); a bigger $d_{min}$ indicates better distribution of the points.

In a $n_v\times n_p$ ($n _v$ levels, $n _p$ variables) design space, the expected experiments trials $n^*$ can be determined by Eq. (9). With TPLHD and $Matlab^{TM}$ method, $n_v\times n^*$ designs were conducted. In order to compare the three methods based on the same ground, the design values were divided by $n_d^s$ and then round up into $[1, n_p]$, to generate the same number of design points with ETPLHD. Three criterions $\phi _p$ in Eq. (3), $d_{min}$ and Time consumption(s) are compared in the three methods.

All experiments were conducted in $Windows^{TM}$ 7 with Intel Core i5-3470 CPU (3.20 GHz), 4 GB RAM, $MATLAB^{TM}$ (R2012a).

Table 1. Performance comparison among ETPLHD, TPLHD and lshdesign

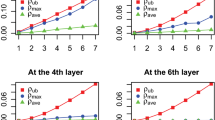
Table 1 shows the results of the three methods. The best $\phi _p$ is shown with bold. It can be concluded that ETPLHD method performs best under experiment space with no more than 5 variables. The only exception is the case where $n_p=4,n_v=4$ and $s=1$. For the design space with 6 variables, TPLHD performs worse than lshdesign with most cases, but ETPLHD is superior to lshdesign basically. In addition, ETPLHD can generate points with least time consumption among the three methods. For all cases, ETPLHD and TPLHD cost less time to obtain an optimal design. By contrast, lhsdesign requires seconds to minutes for a large experiment space.

3 Apply ETPHLD in System Predication

3.1 Linear Regression Prediction Model

The goal of DOE method is to evaluate the target system with less experiment trails. Many approximation methods such as the linear regression, Kriging model, neural nets, support vector regression and so on are often employed to evaluate and then predict the target system. The linear regression is the most used approach among $them^{10}$.

A first-order polynomial can be given by

$$\begin{aligned} {y=X\beta +\textit{e}} \end{aligned}$$

(10)

where $y=(y_1,\ldots ,y_n)^\prime$ is the predicted value of the target system with n experiments. $X=(x_{ij})(i=1,\ldots ,n,j=1,\ldots ,q)$ is the experiment data recorded in n trails, where i in the index of experiment trail, and j is the index of data within each trail. $\beta =(\beta _1,\ldots ,\beta _q)$ is the regression coefficients; and $e=(e_1,\ldots ,e_n)^\prime$ denotes the residuals in each experiment.

Let $w=(w_1,\ldots ,w_n)^\prime$ be the true output of the simulation system, the Sum of Squared Residuals(SSR) is given by Eq. (11)

$$\begin{aligned} {SSR=(y-w)^\prime (y-w)} \end{aligned}$$

(11)

The coefficient vector $\beta$ is defined as follows to compute the predication:

$$\begin{aligned} {\beta =(X^\prime X)^{-1}X^\prime w} \end{aligned}$$

(12)

The accuracy of the model is normally measured by the mean square error (MSE), which is the accurate estimate of the true error of the prediction model.

$$\begin{aligned} {\textit{MSE}=SSR/n} \end{aligned}$$

(13)

where n is the number of experiment trials.

3.2 A Complex Example: The Combat Simulation

There are blue and red force in the combat scenario. The blue force includes a formation of fighters, who attempts to cross a strait to attack the ships of the red. On the other hand, the red ships have the anti-air capacity. Once the blue fighters flight close to the ships, the SAM missiles will be launched to protect the ships (Fig. 4). The relationship between the performance of SAM missile and the shoot-down number of blue fighters is concerned. The combat is simulated using a Computer Generated Force (CGF) platform [10].

Fig. 4.

The two dimension display of the scenario

Five parameters of SAM missile are adopted as the design variables and each has 4 levels, as shown in Table 2.

Table 2. Design parameters and levels

TPLHD and ETPLHD are tested in this scenario for comparison. In ETPLHD, $s=3$ produces 32 experiment points. Each experiment point is tested for 5 times to get the mean value of the output for further analysis. The linear regression approach is employed to obtain an approximated system model that can be used to predict the output of the combat. Table 3 demonstrates a part of the results and the predictions of the approximated models based on the two DOE methods.

Table 3. The true results and the predictions

Given the data in Table 3, the MSE of the two methods can be calculated according to Eq. (13). The MSE of ETPLHD is 0.6141, which is much less than that (1.0533) of TPLHD. This result indicates that the approximated system model using the ETPLHD method performs better than the model using TPLHD method.

20 random points are selected from the experiment space to verify the effectiveness of the approximated models. Table 4 demonstrates a part of the results. $y_a$ is the prediction by the approximated model that uses the TPLHD method, while $y_b$ is the predication by the model that uses the ETPLHD method.

Table 4. Part of results of 20 random points with the two methods

The plots of the simulation values and two prediction values are shown in Fig. 5. The MSE of the two predication is 4.0147 and 3.217 respectively, indicating that the prediction model with ETPLHD is more precise.

Fig. 5.

The simulation and two prediction values of random points

4 Conclusion

In order to break the limitation of the fixed number of design points in traditional LHD method, a new flexible DOE method ETPLHD is proposed in this paper. The comparison shows that ETPLHD method performs better than TPLHD for no more than 6 variables. The ETPLHD method is also applied in a complex combat simulation to help to find proper approximation model of the combat system, which is used to predict the outcomes of the combat with different parameter configurations of the SAM missiles. The results show that the approximation model using the ETPLHD method has better predicting accuracy than the model using the TPLHD method.