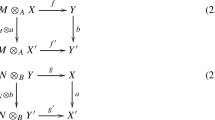Abstract
In this paper, we have studied the properties of semi-projective module and its endomorphism rings related with Hopfian, co-Hopfian, and directly finite modules. We have provide an example of module which are semi-projective but not quasi-projective. We also prove that for semi-projective module M with \(dim M <\infty \) or \(Codim M < \infty \), \(M^n\) is Hopfian for every integer \(n \ge 1\). Apart from this we have studied the properties of pseudo-semi-injective module and observed that for pseudo-semi-injective module, co-Hopficity weakly co-Hopficity and directly finiteness are equivalent. Finally proved that for pseudo-semi-injective module M, N be fully invariant M-cyclic submodule of M with N is essential in M, then N is weakly co-Hopfian if and only if M is weakly co-Hopfian.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
2000 Mathematics Subject Classification
1 Introduction
The notion of quasi-principally projective module was introduced by Wisbauer [14] under the terminology of semi-projective modules. Tansee and Wongwai [11] introduced the idea of M-principally projective module and defined a module M quasi-principally projective if it is M-principally projective. They also established several properties of the endomorphism ring of such modules and proved that quasi-principally projective modules are equivalent to semi-projective module. In this paper, we have established some properties of endomorphism ring of quasi-principally projective module in terms of Hopfian modules and proved that a quasi-principally projective module M is Hopfian if and only if M/N is Hopfian, where N is fully invariant small submodule of M.
2 Preliminaries
Throughout this paper, by a ring R we always mean an associative ring with identity and every R-module M is an unitary right R-module. Let M be an R-module; a module N is called M-generated, if there is an epimorphism \(M^{(I)} \longrightarrow N\) for some index set I. If I is finite then N is called finitely M-generated. In particular, a submodule N of M is called an M-cyclic submodule of M if \(N = s(M)\) for some \(s \in EndM_R\) or if there exist an epimorphism from M to N, equivalently it is isomorphic to M / L for some submodule L of M. A submodule K of an R-module M is said to be small in M, written \(K \ll M\), if for every submodule \(L \subseteq M\) with \(K + L = M\) implies \(L = M\). A nonzero R-module M is called hollow if every proper submodule of it is small in M. A submodule N of M is called fully invariant submodule of M, if \(f(N) \subseteq N\) for any \(f \in S = EndM_R\). A module M is called indecomposable, if \(M \ne 0\) and cannot be written as a direct sum of nonzero submodules.
Consider the following conditions for an R-module M:
\((D_1)\): For every submodule A of M there is a decomposition \(M = M_1 \bigoplus M_2\) such that \(M_1 \subseteq A\) and \(A \cap M_2 \ll M\).
\((D_2)\): If \(A \subseteq M\) such that M / A is isomorphic to a summand of M, then A is a summand of M.
\((D_3)\): If \(M_1\) and \(M_2\) are summands of M with \(M_1 + M_2 = M\), then \(M_1 \cap M_2\) is a summand of M.
An R-module M is called a lifting module if M satisfies \((D_1), M\) is called discrete module if it satisfies \((D_1)\) and \((D_2)\) and quasi-discrete if it satisfies \((D_1)\) and \((D_3)\).
We will freely make use of the standard notations, terminologies, and results of [1, 3, 14].
3 M-Principally Projective Module
Let M be a right R-module. A right R-module N is called M-principally projective

if every R-homomorphism f from N to an M-cyclic submodule s(M) of M can be lifted to an R-homomorphism g from N to M, such that the above diagram is commutative, i.e., \(s \cdot g = f\). A right R-module M is called quasi-principally projective (or semi-projective) if it is M-principally projective. Some examples of semi-projective modules are \(\mathbb Z_4\), \(\mathbb Z_6\) over \(\mathbb Z\) (set of integers). Clearly, every projective module and quasi-projective module are semi-projective. But converse need not be true:
-
1.
The \(\mathbb Z\)-module \(\mathbb Q\) is semi-projective but not quasi-projective.
-
2.
Let R be any integral domain with quotient field \(F \ne R\). Then \(M = F \oplus R\) is semi-projective (but in general not quasi-projective).
-
3.
For any prime p in \(\mathbb Z\), the Prufer p-group \(\mathbb Z(p\infty )\) is not semi-projective.
Now, we provide an example of semi-projective module which is not M-principally projective module.
Example 3.1
Let \(M_1 = \mathbb Z/p\mathbb Z\) and \(M_2 = \mathbb Z/p^2\mathbb Z\) for any prime \(p \in \mathbb Z\) be modules over \(\mathbb Z\). Then we can easily check that both \(M_1\) and \(M_2\) are semi-projective modules. However \(M_1\) is not \(M_2\)-principally projective.
Proposition 3.2
If M is quasi-projective module and K is fully invariant submodule of M then M / K is semi-projective module.
Proof
The Proof is straightforward and hence we omit it.
An R-module M is called Hopfian (resp. co-Hopfian), if every surjective (resp. injective) R-homomorphism \(f : M \longrightarrow M\) is an automorphism. For example, every Noetherian R-modules are Hopfian and every Artinian R-modules are co-Hopfian. A module M is called directly finite, if M is not isomorphic to a proper summand of itself.
Lemma 3.3
(Proposition 3.25, Mohamed and Muller (1990) [6]) An R-module M is directly finite if and only if \(f \cdot g = 1\) implies \(g\cdot f = 1\) for any \(f, g \in End M_R\).
In the following propositions, we relate semi-projective module with Hopfian, co-Hopfian and directly finite modules.
Proposition 3.4
Let M be semi-projective co-Hopfian, then it is Hopfian.
Proof
Let f be surjective endomorphism on M and \(I_M : M \longrightarrow M\) be an identity map on M. By semi-projectivity of M there exists an R-homomorphism \(g : M \longrightarrow M\) such that \(f \cdot g \,=\, I_M\), implies that g is monomorphism. Since M is co-Hopfian, then it follows that \(f \,=\, g^{-1}\) is an automorphism on M. Therefore M is Hopfian.
Proposition 3.5
For the semi-projective modules M, the following statements are equivalent:
(i) M is Hopfian;
(ii) M is co-Hopfian;
(iii) M is directly finite.
Proof
Proof is trivial.
Proposition 3.6
Let M be semi-projective and N is fully invariant small submodule of M. Then M is Hopfian if and only if M / N is Hopfian.
Proof
Assume that M / N is Hopfian. Let \(f : M \longrightarrow M\) be any epimorphism, then semi-projectivity of M implies that there exist an homomorpshim \(g : M \longrightarrow M\) such that \(f \cdot g = I_M\). Hence \(M \cong M \oplus (ker f)\) hence \(K = (ker f)\) is direct summand of M. Since N is fully invariant implies \(f(N) \subseteq N\), now we have induced a map \(f^{'} : M/N \longrightarrow M/N\) which is clearly an epimorphism, the Hopficity of M / N implies that \(f^{'} : M/N \longrightarrow M/N\) is an isomorphism. Now by \((f^{'} . \pi )(K) = (\pi \cdot f )(K) = 0\), where \(\pi : M \longrightarrow M/N\) be natural epimorphism, we see that \(\pi (K) = 0\), it means \(K \subseteq N\), but \(K \subseteq N \ll M\) implies that \(K \ll M\). Since M is semi-projective there exist a splitting for f, i.e., \(K = ker f\) is direct summand of M. Therefore \(K = ker f = 0\), implies that M is Hopfian.
Conversely, assume that M is Hopfian and \(N \ll M\) if \(f : M/N \longrightarrow M/N\) is an epimorphism. We have \(f \cdot \pi : M \longrightarrow M/N\), where \(\pi \) is natural epimorphism from \(M \longrightarrow M/N\). Then by semi-projectivity of M, there exists \(g \in EndM_R\), such that \(\pi \cdot g = f \cdot \pi \) implies that g is an epimorphism by 19.2, Wisbauer (1991) [14] as \(\pi \) is a small epimorphism. Since M is Hopfian then g is an isomorphism.
Assume \(ker f \ne 0\), then there exists \(x \in M\) such that \(f(x + N) = N\) implies \(f .\pi (x) = \pi . g(x) = g(x) + N = N\) gives that \(g(x) \in N \Rightarrow x \in g^{-1}(N) \subseteq N\). It follows that \(ker f = N\), therefore M / N is Hopfian.
Corollary 3.7
Let M be finitely generated semi-projective module. Then M is Hopfian if and only if M / J(M) is Hopfian.
Proof
We know that J(M) is fully invariant submodule of M. If M is finitely generated then we have \(J(M) \ll M\). Thus by the above proposition proof is obvious.
Corollary 3.8
Let M be semi-projective, N and L are submodules of M such that \(N + L = M\) and \(N \cap L \ll M\). Then M / N and M / L are Hopfian.
Proof
We have \(M / (N \cap L) = N / (N \cap L) \oplus L / (N \cap L)\), by above Proposition 3.6, \(M / (N \cap L)\) is Hopfian, hence so its direct summand, as \(N / (N \cap L) \cong (N+L) / L = M/L\), similarly \(L / (N \cap L) \cong (N + L) /N = M/N\) is Hopfian.
The next proposition is the generalization of Pandeya et.al. (Proposition 3.8) [7], whose proof is straightforward and hence we omit it.
Proposition 3.9
Let M be finitely generated semi-projective hollow module then M is directly finite if and only if each homomorphic image is directly finite.
For any module M, we denote the Goldie dimension of M by dimM and the dual Goldie dimension of M by CodimM.
Proposition 3.10
Let M be semi-projective modules with \(dim M < \infty \) or \(Codim M < \infty \). Then \(M^n\) is Hopfian for every integer \(n \ge 1\).
Proof
We can easily seen that \(M^n\) satisfies the hypothesis of the statement, since \(dim M^n = n(dim M), Codim M^n = n(Codim M)\), and M is semi-projective module implies that \(M^n\) is semi-projective. Hence it remains to prove that M is Hopfian. Let \(f : M \longrightarrow M\) be any epimorphism, then semi-projectivity of M implies that there exist an homomorpshim \(g : M \longrightarrow M\) such that \(f \cdot g = I_M\). Hence \(M \cong M \oplus (ker f)\). This yields \(dim M = dim M + dim(ker f)\) and \(Codim M = Codim M + Codim(ker f)\). If \(dim M < \infty \) then first of these equations will imply that \(dim(ker f) = 0\), hence \(ker f = 0\) that is f is an automorphism. If \(Codim M < \infty \), then second of these equations will imply that \(Codim(ker f) = 0\), hence \(ker f = 0\) that is f is an automorphism. Thus in both cases, we get our assumed surjective endomorphism is an automorphism that is M is Hopfian implies that \(M^n\) is Hopfian.
Corollary 3.11
Let M be semi-projective modules with \(Codim M < \infty \). Then for any fully invariant submodule K of M and any integer \(n \ge 1,\) the module \((M/K)^n\) is Hopfian.
Proof
Immediate consequence of Propositions 3.2 and 3.10.
Corollary 3.12
Let R be a ring with \(dim R_R < \infty \). Then \(M_n(R)\) is directly finite for every integer \(n \ge 1\).
Proof
Since \(R_R\) is projective, assume that \(dim R_R < \infty \) then by Proposition 3.9, we see that \(R^n\) is Hopfian for all integer \(n \ge 1\). Then it is proved by the observation that M is Hopfian then \(End M_R \) is directly finite.
Lemma 3.13
Let N be a submodule of a semi-projective module M. Then N is a summand if M / N is isomorphic to a summand of M.
Proof
The Proof is straightforward and hence we omit it.
Therefore, we say that a semi-projective module satisfies \((D_2)\) condition. In general, we have the following implication:
Projective \(\Rightarrow \) Quasi-projective \(\Rightarrow \) semi-projective \(\nRightarrow \) Discrete.
Corollary 3.14
Let M be semi-projective module, then the following statements are equivalent:
(1)M is discrete;
(2)M is quasi-discrete;
(3)M is lifting.
Proof
\((1) \Rightarrow (2) \Rightarrow (3)\) are clear from definitions and \((3) \Rightarrow (1)\) immediate from Lemma 3.13.
Corollary 3.15
An indecomposable semi-projective module M is discrete if and only if M is hollow.
Proof
The Proof is straightforward and hence we omit it.
4 Pseudo-Semi-Injective Modules
Let M be a right R-module. M is called semi-injective if for any M-cyclic submodule N of M, monomorphism \(g : N \longrightarrow M\) and corresponding to any homomorphism \(f : N \longrightarrow M\) there exists a map \(h \in EndM_R\), such that \(h \cdot g = f\), i.e., diagram is commutative.
We wish to consider the situation where the map h in this definition is required to be a monomorphism. For this to happen, a map f must be a monomorphism. This leads to the following definition.
A right R-module M is called pseudo-M-principally injective (or pseudo-semi-injective) if for any M-cyclic submodule N of M and R-monomorphism \(f, g : N \longrightarrow M\) there exists a monomorphism \(h \in EndM_R\), such that \(h \cdot g = f\).
It is easy to show that if M is pseudo-semi-injective module, then every monomorphism in \(EndM_R\) is an automorphism, that is every pseudo-semi-injective module is co-Hopfian.
It is clear that every semi-injective module is pseudo-semi-injective, however, converse need not be true. In the following Proposition, we impose the uniformness on pseudo-semi-injective module that is desirable to make it semi-injective modules.
Proposition 4.1
Every uniform pseudo-semi-injective module is semi-injective.
Proof
Let M be uniform pseudo-semi-injective module and N be M-cyclic submodule of M, let \(f : N \longrightarrow M\) be any homomorphism implies that \(ker f \subseteq N\). If \(ker f = N\) case is trivial. If \(ker f = 0\), then f is a monomorphism which extend to a homomorphism h from M to M. If \(ker f \ne 0\), since N is uniform then it can be easily checked that \(g = I_N - f : N \longrightarrow M\) is injective map that is \(ker g = 0\), where \(I_N: N \longrightarrow M\) be the inclusion map. By definition of pseudo-semi-injectivity of M, there exists an extension h of g from M to M such that \(g = I_N - f = h \cdot i\) implies that \(f = (1- h) \cdot i\), which gives that \((1- h)\) is an extension of f to M. Thus, we conclude that M is semi-injective module.
Corollary 4.2
Every semi-simple pseudo-semi-injective module is semi-injective.
Proposition 4.3
Let M be a pseudo-semi-injective module and \(f : M \longrightarrow M\) be a monomorphism. Then f(M) is a direct summand of M.
Proof
The proof is straightforward and hence we omit it.
Proposition 4.4
Let N be indecomposable pseudo M-principally injective modules, then every element \(f \in EndN_R\) is invertible if and only if \(ker f = 0\).
Proof
The invertible in \(EndN_R\) is just the R-isomorphism from N to N. Thus it is clear that, if f is an invertible elements of \(EndN_R\) then \(ker f = 0\). Conversely suppose that \(ker f = 0\) then f is a monomorphism and f(N) is injective and so pseudo M-principally injective module. Then f(N) is a direct summand of every extension of itself, thus f(N) is a direct summand of N, and \(f(N) \ne 0\) so \(f(N) = N\), since N is indecomposable. Therefore f is a surjective homomorphism and so f is an invertible element of \(EndN_R\).
A R-module M is called weakly co-Hopfian if any injective endomorphism f of M is essential, i.e., \(f(M)\subseteq ^e M\). The set of Integer \(\mathbb Z\) is weakly co-Hopfian but not co-Hopfian.
Proposition 4.5
Let M be pseudo-semi-injective module, then the following statements are equivalent:
(i)M is co-Hopfian;
(ii)M is weakly co-Hopfian;
(iii)M is directly finite.
Proof
\((1) \Rightarrow (2) \Rightarrow (3)\) are trivial. For \((3) \Rightarrow (1)\) Assume that \(f : M \longrightarrow M\) be an injective endomorphism, then \(f(M) \cong M\) and so f(M) is pseudo-M-principally injective. Thus, f(M) is direct summand of M that is there exist a submodule K of M such that \(f(M) \oplus K = M\). Hence, \(M \oplus K \cong M \Rightarrow K = 0\) since M is directly finite. Therefore, \(f(M) = M\) implies that f is surjective and hence M is co-Hopfian.
Corollary 4.6
If M is indecomposable pseudo-semi-injective module, then it is co-Hopfian.
Proposition 4.7
Let M be pseudo-semi-injective and nonsingular module. Then M Hopfian if and only if M co-Hopfian.
Proof
Let M is co-Hopfian and \(f : M \longrightarrow M\) be surjective endomorphism of M. Then M / kerf is nonsingular, and so kerf is essentially closed in M. since M is pseudo-semi-injective modules, then kerf is also pseudo-semi-injective. Thus, \(M \cong M \oplus ker f\). As M is co-Hopfian, it is directly finite module by Proposition 4.5, so the above isomorphism implies that \(ker f = 0\), i.e., f is an automorphism. Thus M is Hopfian. Conversely, It is well known that every Hopfian and co-Hopfian modules is directly finite so prove is done in the light of Proposition 4.5.
Proposition 4.8
Let M be pseudo-semi-injective module and N be fully invariant M-cyclic submodule of M with N is essential in M. Then N is weakly co-Hopfian if and only if M is weakly co-Hopfian.
Proof
A sume that N is weakly co-Hopfian. Let \(f : M \longrightarrow M\) be an injective endomorphism then by Proposition 2.3, f(M) is direct summand of M. Since N is fully invariant \(f(N) \subseteq N\). Thus \(f|_N : N \longrightarrow N\) is an injective homomophism, the weakly co-Hopficity of N implies that \(f(N) \subseteq ^e N\), since \(N \subseteq ^e M\) we deduce that \(f(N) \subseteq ^e M\) and we have \(f(N)\subseteq f(M)\subseteq M\), thus \(f(M) \subseteq ^e M\) therefore M is weakly co-Hopfian.
Conversely, let \(f : N \longrightarrow N\) be an injective endomorphism and \(i : N \longrightarrow M\) be an inclusion map. Since M is pseudo-semi-injective module, there exists a monomorphism \(h : M \longrightarrow M\) such that \(i \cdot f = h \cdot i\). Since M is weakly co-Hopfian by Proposition 4.5, M is co-Hopfian, so h is an isomorphism. N is fully invariant M-cyclic submodule of M so it is pseudo-semi-injective and \(h(N) \subseteq N \Rightarrow h^{-1}(N) \subseteq N\) so \(h(N) = N\). But \(f = h|_N\) hence \(f : N \longrightarrow N\) is surjective, so N is co-Hopfian then by Proposition 4.5, proof is complete.
References
Anderson, F.W., Fuller, K.R.: Rings and Categories of Modules. Springer, New York (1974)
Birkenmeier, G.F., Muller, B.J., Rizvi, S.T.: Modules in which every fully invariant submodule is essential in a direct summand. Commun. Algebr. 30, 1395–1415 (2002)
Clark, J., Lomp, C., Vanaja, N., Wisbauer, R.: Lifting Modules Supplements and Projectivity in Module Theory. Birkhauser, Boston (2006)
Ghorbani, A., Haghany, A.: Generalized hopfian modules. J. Algebr. 255, 324–341 (2002)
Haghany, A., Vedadi, M.R.: Study of semi-projective retractable modules. Algebr. Coll. 14(3), 489–496 (2007)
Mohamed, S.H., Muller, B.J.: Continuous and Discrete module. Cambridge University Press, Cambridge (1990)
Pandeya, B.M., Pandey, A.K.: Almost perfect ring and directly finite module. Int. J. Math. Sci. 1(1–2), 111–115 (2002)
Patel, M.K., Pandeya, B.M., Gupta, A.J., Kumar, V.: Generalization of semi-projective modules. Int. J. Comput. Appl. 83(8), 1–6 (2013)
Patel, M.K., Pandeya, B.M., Gupta, A.J., Kumar, V.: Quasi-principally injective modules. Int. J. Algebr. 4, 1255–1259 (2010)
Rangaswami, K.M., Vanaja, N.: Quasi Projective in abelian categories. Pac. J. Math. 43, 221–238 (1972)
Tansee, H., Wongwai, S.: A note on semi projective modules. Kyungpook Math. J. 42, 369–380 (2002)
Varadarajan, K.: Properties of endomorphism rings. Acta. Math. Hungar. 74(1–2), 83–92 (1997)
Kumar, V., Gupta, A.J., Pandeya, B.M., Patel, M.K.: M-SP-Injective module. Asian Eur. J. Math. 5, 1–11 (2011)
Wisbauer, R.: Foundation of Module and Ring Theory. Gordon and Breach, London (1991)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer Science+Business Media Singapore
About this paper
Cite this paper
Patel, M.K. (2016). Properties of Semi-Projective Modules and their Endomorphism Rings. In: Rizvi, S., Ali, A., Filippis, V. (eds) Algebra and its Applications. Springer Proceedings in Mathematics & Statistics, vol 174. Springer, Singapore. https://doi.org/10.1007/978-981-10-1651-6_19
Download citation
DOI: https://doi.org/10.1007/978-981-10-1651-6_19
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-10-1650-9
Online ISBN: 978-981-10-1651-6
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)