Why Do Hives Die? Using Mathematics to Solve the Problem of Honey Bee Colony Collapse

Abstract

Honey bees are vital to the production of many foods which need to be pollinated by insects. Yet in many parts of the world honey bee colonies are in decline. A crucial contributor to hive well-being is the health, productivity and longevity of its foragers . When forager numbers are depleted due to stressors in the colony, such as disease or malnutrition, or in the environment, such as pesticides, this causes a reduction in the amount of food (nectar and pollen) that can be collected and a reduction of the colony’s capacity to raise brood (eggs, larvae and pupae) to produce new adult bees. We use a set of differential equation models to explore the effect on the hive of high forager death rates. We track the population of brood; hive bees who work inside the hive; foragers who bring back food to the hive; and stored food. Using data from experimental research we devised functions that described the effect of the age that bees first become foragers on their success and lifespan as foragers. In particular, we examine what happens when bees become foragers at a comparatively young age and how this can lead to a sudden rapid decline of adult bees and the death of the colony.

1 Section Heading

Growing crops for food is arguably the oldest human industry. Food crops need to be pollinated to produce fruit or seed, either for consumption or to sow for the next crop. Cereals such as rice, wheat and maize are pollinated by wind, but almost all other crops require insects to transfer pollen from one flower to another to set the seed. Honey bees (Apis mellifera ) are the most important pollinators of commercial crops and so the survival and health of honey bee colonies is vital for food security worldwide.

Individual honey bees only survive as part of a colony or hive, usually of several thousand bees. Bees in each colony collectively gather food and raise brood (that is, eggs, larvae and pupae) from eggs laid by a single queen [19]. Labour in the colony is self-organised in response to pheromonal and behavioural cues that are generated by interactions between adult bees, brood and food. In a commercial apiary, if all the bees in a hive die or abandon the colony, this leads to a financial loss to the apiarist who must either establish a new colony or suffer the loss of productive capacity.

In the last decade or more, the rate of honey bee colony failure has increased significantly and the number of commercial colonies has declined, particularly in the USA but also in Europe and Japan [11]. Colony failure includes overwintering losses in cold climates and loss due to diseases, pesticide exposure or the Varroa mite [11, 18]. One of the more puzzling types of colony loss is where previous healthy hives are found abandoned by adult bees, still containing stored food and dead brood, but with few or no adult bee, and few dead bees [16]. There may be no obvious cause for this very rapid depopulation of the hive. This phenomenon has become known as colony collapse disorder (CCD) . It usually occurs in late spring or early summer, just as hives have emerged from their winter hibernation and are reaching their peak summer numbers.

There is now general agreement among bee biologists that there are many causes of CCD and these can include anything which puts a hive under stress, including diseases, parasites, pesticide use in the hive environment, apicultural practices such as keeping large number of hives close together or poor nutrition, due, for example to the hive foraging from a single type of plant including agricultural monocultures such as almond orchards or canola crops [2, 5]. All of these put stress on the hive but the presence of these stressors alone does not explain the mechanism of the sudden depopulation that hives experience in CCD.

In this paper, we use mathematical models for the population of adult bees, brood and food in the hive to explore the hypothesis that the mechanism that drives CCD is sustained high death rates of foragers which causes adult bee numbers to become depleted and leads to hive death.

Our hypothesis that high forager death rates drive hive collapse depends crucially on the population dynamics of the hive. All eggs in the hive are laid by a single queen bee. After 3 days a egg hatches into a larvae which is fed and cared for by worker bees in the hive. The larvae pupates after 9 days and 12 days later the adult bee emerges from pupation. Young adult bees remain in the hive, caring for brood and for the queen, storing food that is brought back by foragers and doing other in-hive work. Older bees become foragers and leave the hive to gather nectar and pollen to supply the colony with food. Foragers are exposed to many hazards in the environment outside the hive and, as foraging itself is a metabolically expensive and risky activity, forager lifespan is generally less than 7 days from the time a bee starts to forage [17]. If a forager is diseased or malnourished, then her lifespan is likely to be shorter than that of a healthy forager in the same environment.

The transition from hive bee to forager is controlled by social feedback. If there are many foragers, then hive bees tend not to become foragers; if there are few foragers, however, then older hive bees will become foragers. This social inhibition is mediated by the pheromone ethyl oleate, which is produced by foragers [9]. Food shortages also stimulate hive bees to become foragers [14]. This, potentially enables a hive to survive a temporary shortage of food when food storage returns to normal levels within a few days.

It is well known that large hives raise a higher proportion of eggs to adulthood [1]. Larger populations of hive bees and foragers can give more care and find more food for larvae and other brood. When food is short, however, hive bees cannibalise some larvae and eggs to feed older larvae. Hence food shortages also reduce the number of brood raised to adults.

We will construct two differential equation models that represent the interactions between hive bees, foragers, food and brood. The first model can easily be analysed to show the bifurcation behaviour of the system and, in particular, what happens to the steady-state solutions as forager death rates increase. The second model takes into account the effect of the age that bees first become foragers on forager recruitment, survival and efficacy. This second model cannot be easily analysed, except numerically, but produces the rapid collapse of hive populations that is observed by apiarists.

2 A Basic Model for the Dynamics of Food, Brood, and Hive Bee and Forager Populations

We use a system of four differential equations to model the interactions illustrated in Fig. 1. In the model, we will only consider uncapped brood, that is, eggs and larvae. When a larva pupates, the hive bees cap the cell in the brood comb which the pupa occupies with a wax cap. When the adult bee emerges from pupation she chews through the cap. The pupae or capped brood are not represented explicitly in the model, but their presence is modelled by a delay between uncapped brood going into pupation and emerging as adults 12 days later.

The independent variable in the model is time t, measured in days. The dependent variables are f representing stored food within the hive, B, the number of uncapped brood items, H, the number of hive bees and F, the number of foragers. This model was first presented in [8] and is based on a simpler model that represented foragers and hive bees only [7].

Fig. 1

A flow chart showing processes and interactions in the honey bee colony that are represented in the model. The grey arrow and labelling on the right-hand side of the chart describe death of bees during transition to foraging which is included in the extended model with age dependence but not in the basic model

2.1 Model Equations

Food is collected by foragers and consumed by foragers, hive bees and brood. The difference between the rate of food collection and food consumption gives the rate of accumulation or depletion of stored food f:

$$\begin{aligned} \frac{df}{dt} = c F - (\gamma _B B +\gamma _H H + \gamma _F F). \end{aligned}$$

(1)

Here c is the weight of food in grams collected per forager per day and $\gamma _B$, $\gamma _H$ and $\gamma _F$ are the average weight of food consumed per day by each brood item, hive bee or forager, respectively. For ease of analysis, we assume that all adult bees consume the same amount of food on average, so we set $\gamma _H = \gamma _F = \gamma _A$. Hence

$$\begin{aligned} \frac{df}{dt} = c F - \gamma _B B -\gamma _A (H + F). \end{aligned}$$

(2)

In the model we include only brood that survives to adulthood. These brood items are a proportion of the total number of eggs laid by the queen and we model their rate of pupation as a linear rate proportional to the number of uncapped brood items. Hence

$$\begin{aligned} \frac{dB}{dt}=L\, S(H,f)-\phi B, \end{aligned}$$

(3)

where L is the laying rate of the queen in number of eggs per day, $\phi$ is the rate of pupation in brood numbers per day where $1/\phi$ is the time that a brood item spends as uncapped brood, which is known to be 9 days hence $\phi = 1/9$. The function S(H, f) gives the proportion of eggs that survive to become adult bees. This will depend on the number of hive bees and the amount of stored food, particularly when stored food levels are low. We model S(H, f) as follows:

$$\begin{aligned} S(H,f) = \frac{f^2}{f^2 + b^2} \, \frac{H}{H+ \nu } \end{aligned}$$

(4)

where the parameters b and $\nu$ determine how quickly S(H, f) approaches one as f and H increase, respectively. The function S(H, f) saturates both with respect to food f and also with respect to hive bee numbers H. Clearly, the number of brood that is raised to adulthood cannot continue to increase indefinitely as food stocks and hive bee numbers increase. There is a maximum number of brood that a hive can raise and this maximum is determined by the queen’s laying rate L. We assume that the proportion of brood raised increases linearly with the number of hive bees when H is low, but that the dependence on food stores is sigmoidal, due to the need for hive bees to spend more time finding food inside the hive when stored food f is very low.

Hive bees emerge $\tau$ days after they become pupae. Bees leave the hive bee class to become foragers. Generally speaking, the hive is a very safe environment with low adult bee mortality, so we do not include death of hive bees in the model. We model the change of hive bee population as

$$\begin{aligned} \frac{dH}{dt} = \phi B (t-\tau )-R(H,F,f) \, H \end{aligned}$$

(5)

where the function R(H, F, f) governs the recruitment rate of hive bees to the forager class. This rate is determined both by the proportion of foragers in the colony and by the availability of food stores. We model the recruitment function as

$$\begin{aligned} R(H,F,f) = \alpha _\mathrm{min} + \alpha _\mathrm{max}\left( \frac{b^2}{b^2+f^2}\right) -\sigma \left( \frac{F}{F+H}\right) \end{aligned}$$

(6)

where $\alpha _\mathrm{min}$ is the rate that hive bees become foragers when there are no foragers but plenty of food in the hive, $\alpha _\mathrm{max}$ determines the strength of the effect that low food stores have on forager recruitment and $\sigma$ governs the effect of social inhibition on recruitment. If stored food is plentiful, then recruitment essentially does not depend on food at all, but only on the proportion of foragers to the total number of adult bees in the hive. If this proportion is high, bees are inhibited from becoming foragers and the rate of recruitment is low. Conversely, if there is a very low proportion of foragers among the adult bees of the hive, then inhibition is weak and recruitment is high. The constant $\alpha _\mathrm{min}$ is the rate of recruitment when there is plentiful stored food but no foragers. The constant $\alpha _\mathrm{max}$ governs the effect of food shortage on recruitment.

Foragers are recruited from the hive bee class and die at a linear rate:

$$\begin{aligned} \frac{dF}{dt} = R(H,F,f) H -\mu F. \end{aligned}$$

(7)

Here the first term models recruitment and the second term represents forager death where $\mu$ is the forager death rate.

Fig. 2

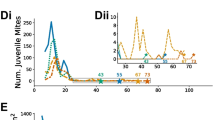
Results from the basic model. Population and stored food as a function of time for different values of forager death rate $\mu$. Food is represented by the solid curve, brood by the dotted curve, hive bees by the dot-dash curve and foragers by the dashed curve. Parameter values are $L = 2000$, $\phi = 1/9$, $\nu = 5000$, $\sigma = 0.75$, $\alpha _\mathrm{max} = 0.25$, $\alpha _\mathrm{min} = 0.25$, $b = 500$, $c = 0.1$, $\gamma _A = 0.007$, $\gamma _B=0.018$ and $\tau = 12$. See [8] for a justification of these values. Initially all simulations had 20,000 hive bees, 10,000 foragers and no brood or food. For a $\mu = 0.1$, b $\mu = 0.2$, c $\mu = 0.43$ and d $\mu = 0.55$. Note that the vertical scale on c and d is different to that on a and b

2.2 Results from the Basic Model

Figure 2 shows how the population of a model colony evolves for different forager death rates. When the death rate is low, with $\mu = 0.1$ (so 10 % of foragers are lost each day), the hive has a large population of both adult bees and brood, and food stores increase without bound. Such a hive is in an ideal state for honey production as well as providing many pollinators to the surrounding area.

A higher death rate, $\mu = 0.2$, produces a hive with a smaller number of adult bees, although the brood population is not affected very much which suggests that the hive raises a similar number of adult bees, but that adult bees have a shorter lifespan. Food continues to increase but not as rapidly as when $\mu = 0.1$.

When death rates become highly elevated, then food stores in the model colony do not grow. When $\mu = 0.43$ the population of adult bees is very low compared to when $\mu = 0.1$ and, in fact, there are now fewer hive bees than uncapped brood. Nevertheless, the hive remains viable.

When $\mu$ is raised further, however, the hive collapses. The model shows an exponential decline in both adult bee and brood numbers and within 250 days, its population has dropped below 1000 adults, which is approximately the lowest number of bees a hive needs to survive. At the same time, about 500 g of stored food remains in the hive, even after the bees are nearly all dead.

Equations 2–7 can be solved analytically at steady state to obtain a bifurcation diagram with steady-state solutions as a function of forager death rate $\mu$ as shown in Fig. 3. When food grows unboundedly we ignore Eq. 2 and assume $f\rightarrow \infty$ in 3–7. The weight of residual stored food was calculated numerically when bee numbers are zero at steady state.

Fig. 3

Steady-state solutions as a function of forager death rate $\mu$. Food is represented by the solid curve, brood by the dotted curve, hive bees by the dot-dash curve and foragers by the dashed curve. Parameter values are the same as in Fig. 2. The vertical lines at $\mu = 0.402$ and $\mu = 0.462$ separate the plot into regions with qualitatively different solution behaviour

When $\mu$ is low, that is $\mu < 0.402$ for this parameter set, food grows unboundedly. As $\mu$ increases within this range, the number of adult bees drops significantly while brood numbers are less sensitive to forager death rate.

For $0.402< \mu <0.462$, stored food does not grow unboundedly but has a finite steady state. At $\mu \approx 0.402$ the solution curves for adult bee and brood populations have a slope discontinuity in the bifurcation diagram which suggests that the processes that govern the steady-state values have changed. In particular, it suggests that stored food determines the bee populations when f remains finite. In this regime, increasing $\mu$ affects both adult bee and brood populations to the same degree, unlike in the case where f is unbounded where adult bee populations are much more sensitive to changes in $\mu$ than brood populations.

When $\mu > 0.462$ then bee populations go to zero as $t \rightarrow \infty$. However, by numerically solving Eqs. 2–7 it is evident that stored food is not zero even when bee populations are arbitrarily close to zero. This can be seen in Fig. 3. This result is in agreement with observations of hives that experience CCD as apiarists report that collapsed hives do have food stores remaining, so that starvation is clearly not the sole cause of CCD .

The results from the basic model demonstrate that high forager death rates, on their own can lead to the death of a colony. However, this model predicts that the decline of the colony will be slow, rather than the rapid decline observed in real colonies that experience CCD . This suggests that there is an important aspect of collapsing colony behaviour that is missing from the basic model.

3 Model Incorporating the Effects of Forager Age

Foraging is a task that is physically and cognitively demanding for the individual bee. Her wing muscles must be strong and well developed to carry her perhaps kilometres from the hive; she must be able to navigate accurately and successfully through the environment outside the hive; and she must be able to locate and recognise suitable sources of nectar and pollen and exploit them efficiently. When adult bees emerge from pupation, their brains and wing muscles are not yet mature and the time that each bee spends as a hive bee allows her to mature sufficiently to become a successful forager. It is well known that bees that become foragers when they are too young die sooner and do not forager as effectively as bees that become foragers at a later age [15, 20].

In the basic model, the length of time that a hive bee spends in the hive before she becomes a forager or, alternatively, her age at commencement of foraging a is the reciprocal the recruitment function R(H, F, f):

$$\begin{aligned} a = \frac{1}{R(H,F,f)}. \end{aligned}$$

(8)

Recent experiments by Perry and coworkers [12] have determined the effect of the age of commencement of foraging a on the number of foraging trips a forager makes each day and forager death rate. These researchers also observed that bees which started to become foragers at a young age, often did not make a successful transition to foraging. As part of the transition to foraging, hive bees undertake several exploratory flights outside the hive, for a total of approximately 30 min. Bees that started to make this transition too young were likely not to survive this exploratory phase and so successful transition to foraging was also age dependent.

We extended the model to include the effects of age of commencement of foraging [12]. In the extended model, forager death rate is given by $\mu = m_r\,M(a)$ where M(a) is the forager death rate, dependent on a the age that a bee commences foraging and $m_r$ is the ratio of the death rate in a stressed hive to the death rate in a healthy hive. We made the rate of food collection c dependent on a so that $c = c_TN(a)$ where $c_T$ is the weight of food in grams that is collected in each foraging trip and N(a) is the average number of foraging trips made per day by a bee who commences foraging at age a. We also introduced function T(a) which gave the proportion of hive bees that successfully made the transition to foraging, so that bees left the hive bee class at a rate $R(H,F,f)\, H$ but arrived in the foraging class at a rate $T(a) \, R(H,F,f)\, H$.

The extended model consists of four differential equations and one algebraic equation:

$$\begin{aligned} \frac{df}{dt}= & {} c_TN(a) F - (\gamma _B B +\gamma _H H + \gamma _F F)\end{aligned}$$

(9)

$$\begin{aligned} \frac{dB}{dt}= & {} L\frac{f^2}{f^2 + b^2} \, \frac{H}{H+ \nu }-\phi B\end{aligned}$$

(10)

$$\begin{aligned} \frac{dH}{dt}= & {} \phi B (t-\tau )-R(H,F,f) \, H\end{aligned}$$

(11)

$$\begin{aligned} \frac{dF}{dt}= & {} T(a) R(H,F,f) H - m_rM(a) F\end{aligned}$$

(12)

$$\begin{aligned} a= & {} \frac{1}{R(H,F,f)} \end{aligned}$$

(13)

where R(H, F, f) is given by Eq. 6 as before. Plots of the three functions N(a), M(a) and T(a) are shown in Fig. 4. The functions N(a) and M(a) model data points which are shown in Fig. 4 (although they are not statistically fitted to this data), but T(a) is modelled based on qualitative observations. Note that these equations are essentially the same as Eqs. 2–6, except that they include the functions N(a), M(a) and T(a). Fundamentally, these functions are dependent on the recruitment function $R(H,F,f) = 1/a$ and so the differential equations above could be written as functions of f, B, H and F only. However, the age a that foragers commence foraging is an important biological quantity. Writing these equations in terms of a and including Eq. 13 is not only neater, but also conveys the biological importance of these additional functions, N(a), M(a) and T(a) more clearly.

Fig. 4

Plots of the functions dependent on age of commencement of foraging a in the extended model. a N(a), the average numbers of trips per day; b M(a) the death rate as a function of a; c T(a) the proportion of hive bees that successfully make the transition to foragers

3.1 Results of the Extended Model

Figure 5 shows how model populations and stored food change as a function of time for various values of $m_r$ in the extended model.

Fig. 5

Solutions of the extended model showing the changes in brood, hive bee and forager populations, stored food and the age of commencement of foraging as a function of time for different values of $m_r$. Food is represented by the thin solid curve, brood by the dotted curve, hive bees by the dot-dash curve, foragers by the dashed curve and age of commencement of foraging is represented by the thick solid line. Parameter values and initial conditions are the same as in Fig. 2. The functions N(a), M(a) and T(a) are as shown in Fig. 4. a $m_r= 1$; b $m_r=1.6$; c $m_r = 1.91$; d $m_r=2.0$. Note that the vertical scale on c and d is different to that on a and b

For sufficiently low values of $m_r$, food increases unboundedly. The age of commencement of foraging is more than 20 days for a healthy hive and drops as $m_r$ declines. As in the basic model, as death rates increase with increasing $m_r$ the number of adult bees declines, but brood numbers are not significantly affected.

When $m_r = 1.91$, stored food does not increase without bound, although the populations of brood, hive bees and foragers appear to stabilise and there is no evident collapse. However, when $m_r = 2$, the populations, which initially look similar to those when $m_r = 1.91$ for $t < 70$ days collapse rapidly in 30 days from about 12,000 adult bees to no foragers and only hive bees that are less than 2 days old and so unable to make the transition to foragers. Stored food declines monotonically after about $t = 20$.

The effect of increasing death rates on the age of adult bees can be seen explicitly in the extended model. As $m_r$ increases from 1 to 1.6, to 1.91 the age at steady state when hive bees become foragers decreases from 23 to 13 to 9 days. Bees will have a shorter lifespan as foragers when $m_r$ is higher, as well as starting to forage at a younger age.

These results suggest that the dependence of forager lifespan and efficacy on the age that a bee first starts to forage is crucial in CCD . As foragers die, social inhibition is reduced and so hive bees become foragers more rapidly and hence at a younger age. Younger foragers have shorter lifespans and bees who become foragers when they are younger than 10 days old, make fewer foraging trips on average as their age of commencement of foraging declines. This poor rate of food collection has an effect on stored food and as this decreases, it starts to have an impact on brood raising via S(H, f) (Eq. 4) and also promotes an increased rate of recruitment via R(H, F, f) (Eq. 6). Eventually, stimulated by very low food stores, hive bees are becoming foragers and leaving the hive as soon as possible and dying rapidly either during or after transition to foraging as they do not have the maturity to survive long outside the hive. This leads to a colony with some residual food stores, a low level of brood and comparatively few remaining adult bees which is what is observed in CCD .

Numerical solutions to the extended model show that forager age and adult bee populations at the steady state that corresponds to a viable colony, decline as $m_r$ gets larger (Fig. 6). When $m_r$ reaches a critical value, the solution for a viable colony population no longer exists and the colony will collapse as $t \rightarrow \infty$. The numerical solution shown in Fig. 6 suggests that there is a bifurcation where the steady state corresponding to a viable population is lost.

Fig. 6

Plot showing the approximate steady-state population of adult bees as a function of $m_r$. The steady-state population presented is calculated numerically by solving the extended model Eqs. 10–13 with the same initial conditions and parameter values used in Fig. 2 and taking the population values at $t =1000$ as an approximation for the steady-state value. The slope discontinuity at $m_{r} \approx 1.4$ is due to the slope discontinuity in T(a) which is illustrated in Fig. 4

Figure 5 suggests that when this collapse occurs it is driven by a slow decline in food stores which slowly increases the rate of recruitment, and consequent loss, of foragers as the recruitment rate increases as stored food becomes scarce. To further explore the effect of stored food on the steady state, we took f as fixed and analytically calculated the steady-state values of B, F, H and a as a function of $m_r$ for different fixed values of f. This effectively produced a bifurcation diagram with a series of bifurcation curves shown in Fig. 7. When f is very low, the solution curves have a fold bifurcation with two stable steady states, one that corresponds to a viable population and one that corresponds to a collapsed colony. Once f is greater than about 550, then there is no fold and the only steady state corresponds to a viable population.

Fig. 7

A bifurcation diagram showing a series of solution curves, each for a different fixed value of f, between $f=100$ and $f=700$. The bifurcation parameter is $m_r$ and the age of commencement of foraging is used as the measure of the solution

For $m_r=m^*_r$, a fixed value of $m_r$, both the age of commencement of foraging and the populations of adult bees will decrease at steady state as f decreases. There is a critical value of f, $f_{crit}$ such that when $f=f_{crit}$, the upper bifurcation point on the solution curve is at $m_r = m_r^*$. When $f > f_{crit}$ then the steady state that corresponds to a viable colony exists, but when $f < f_{crit}$ then there is only one steady state and this corresponds to a collapsed colony. Thus if f is declining very slowly then the colony populations will decline slowly until $f=f_{crit}$ when the population will collapse.

This brief, qualitative discussion suggests the possibility of a need for a more comprehensive and rigorous analysis to determine the factors that govern the existence and timing of population collapses in the extended model.

4 Conclusions and Opportunities from Mathematical Models for CCD

The models presented here support the hypothesis that sustained high forager death rates, along with the decreased forager survival and efficacy with decreasing age, leads to CCD . This has yet to be tested in the field, but forager loss is a mechanism that is consistent with our understanding that CCD has many causes, each of which produce stress in the hive [3]. Pesticide use, for example, clearly causes increased forager mortality directly but also indirectly as sublethal effects reduce the quality of the foraging force [6] and increase susceptibility to disease [13]. Diseases in the hive, also contribute to forager mortality, both directly through death due to disease and because foragers that are diseased will tend to have less energy and may be cognitively compromised and so will make fewer foraging trips and may become lost more easily [10]. Likewise, malnourished foragers are likely to collect less food and have a shorter lifespan than healthy bees. Therefore, although the mechanism of CCD proposed in this model is quite specific, the underlying causes of CCD can be very diverse and still produce the same sustained high forager death rate that we hypothesise leads to CCD [3].

Once we understand the mechanism of CCD then we can explore possible solutions. The model suggests different data from hives that can be monitored to identify colonies that are vulnerable to collapse. One clear result from both models is that adult bee numbers are much more sensitive to forager loss than brood numbers and so apiarists should monitor adult bee numbers rather than brood numbers to determine colony health and vulnerability to CCD.

Models also allow us to explore different ways to prevent vulnerable colonies from collapsing. One very simple potential approach to rescue collapsing colonies is in-hive feeding where food is put directly into the hive. This is easy to incorporate into the models. With in-hive feeding, the equation for f in the extended model becomes

$$\begin{aligned} \frac{df}{dt} = c_TN(a) F - (\gamma _B B +\gamma _H H + \gamma _F F) + C \end{aligned}$$

(14)

where C is the rate, in grams/day, that food is put into the hive. Figure 8 shows how feeding the colony even quite small amounts (60 g of food per day) enables it to survive. In an apicultural setting, hives can be fed for a short time, until forager mortality is reduced and the hive is able to maintain a viable population without feeding. Although there are costs associated with in-hive feeding these are likely to be less than the costs of replacing collapsed colonies.

Fig. 8

Plots showing the effect of in-hive feeding. Food is represented by the thin solid curve, brood by the dotted curve, hive bees by the dot-dash curve, foragers by the dashed curve and age of commencement of foraging is represented by the thick solid line. For both plots $m_r=2$. Plot a is the same simulation as in Fig. 5d showing hive collapse. Plot b is exactly the same simulation but with in-hive feeding (Eq. 14), with $C =60$. All parameter values and initial conditions are the same as Fig. 5

Finally, demographic models for honey bee colonies, such as these, can be used as platforms to develop more complicated models that explicitly incorporate the effect of disease [4]. Many diseases and parasites including the Varroa mite affect bees differently at different stages of their life cycle. Demographic models for honey bee colonies, offer the potential to explore disease dynamics and prevention strategies more closely.

Mathematical modelling will never replace field studies of honey bee health and behaviour. However, models are a valuable complement to experimental studies, particularly for exploring hypotheses and predicting the outcomes of complex interactions within honey bee colonies. Models can show what are the likely consequences of colony behaviours and help experimental researchers to focus their efforts on the most important processes in colony dynamics. Together modellers and experimental researchers can ensure that research into honey bee health, which profoundly impacts food production and therefore food security , is both timely and effective.