Keywords

1 Introduction

The wide applications of functionally graded materials (FGMs) in space vehicles, nuclear reactor, defence industries and chemical plants have attracted many researchers throughout the world. FGMs are microscopically inhomogeneous materials whose mechanical properties vary continuously in one or more directions [1]. In a metal-ceramic FGM, the metal-rich side is placed in regions where mechanical properties, such as toughness need to be high whereas the ceramic-rich side which has low thermal conductivity and can withstand high temperatures is placed in regions of large temperature gradients. Due to these characteristics, FGM plate-type components of different geometries are extensively used as structural elements in various fields of modern science and technology.

A lot of studies have been concerned dealing with the vibration characteristics of FGM plates and reported in Refs. [2–12], to mention a few. Out of these, Jha et al. [2] have presented a critical review of recent research on functionally graded plates till 2012. Ferreira et al. [3] used collocation method to analyse the free vibrations of functionally graded rectangular plates of various aspect ratios. Zhao et al. [4] used element-free kp-Ritz method for free vibration analysis of rectangular and skew plates with different boundary conditions taking four types of functionally graded materials on the basis of first-order shear deformation theory. Liu et al. [5] have analysed the free vibration of FGM rectangular plates with in-plane material inhomogeneity using Fourier series expansion and a particular integration technique on the basis of classical plate theory. Free vibration analysis of functionally graded thick annular plates with linear and quadratic thickness variation along the radial direction is investigated by Tajeddini and Ohadi [6] using the polynomial-Ritz method. The vibration behaviour of rectangular FG plates with non-ideal boundary conditions has been studied by Najafizadeh et al. [7] using Levy method and Lindstedt–Poincare perturbation technique. The free vibrations of FGM circular plates of variable thickness under axisymmetric condition have been analysed by Shamekhi [8] using a meshless method in which the point interpolation approach is employed for constructing the shape functions for Galerkin weak form formulation. Chakraverty and Pradhan [9] have applied Rayleigh–Ritz method to study the free vibrations of exponentially graded rectangular plates subjected to different combinations of boundary conditions in thermal environment using Kirchhoff’s plate theory. Recently, Dozio [10] has derived first-known exact solutions for free vibration of thick and moderately thick FGM rectangular plates with at least on pair of opposite edges simply supported on the basis of a family of two-dimensional shear and normal deformation theories with variable order. Very recently, the natural frequencies of FGM nanoplates are analysed by Zare et al. [12] for different combinations of boundary conditions by introducing a new exact solution method.

The aforementioned survey of the literature reveals that there is almost no work on the vibration analysis of functionally graded circular plate of variable thickness using classical plate theory. Keeping this in view, the present paper analyses the axisymmetric vibrations of FGM circular plate of linearly varying thickness based on classical plate theory. Differential transform method (DTM) which is a semi-analytical technique has been employed to obtain the frequency equation. This resulting equation has been solved using MATLAB to get the frequencies. The material properties, i.e. Young’s modulus and density are assumed to vary in the thickness direction according to a power law distribution. The effect of various parameters such as volume fraction index g and taper parameter γ on the natural frequencies have been illustrated for the first three modes of vibration. Three-dimensional modes shapes for a specified plate and for the first three modes of vibration have been plotted. For the validation of the present results, a comparison of results with the existing literature has been made which ensure the versatility of the present technique.

2 Mathematical Formulation

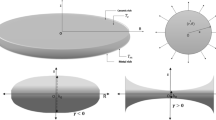
Consider a two-directional functionally graded circular plate of radius a, thickness h, mass density ρ and subjected to hydrostatic in-plane tensile force N 0. Let the plate be referred to a cylindrical polar coordinate system (R, θ, z), z = 0 being the middle plane of the plate. The top and bottom surfaces are \(z = + h/2\) and \(z = - h/2\), respectively. The line R = 0 is the axis of the plate. The equation of motion governing transverse axisymmetric vibration of the present model (Fig. 1) is given by [13]

Fig. 1
figure 1

Geometry and cross-section of tapered FGM circular plate

Full size image
$$\begin{aligned} & Dw_{,RRRR} + \frac{2}{R}\left[ {D + R\,D_{,R} } \right]w_{,RRR} + \frac{1}{{R^{2} }}\left[ { - D + R\,(2 + \nu )D_{,R} + R^{2} D_{,RR} } \right]w_{,RR} \\ & \quad + \frac{1}{{R^{3} }}\left[ {D - R\,D_{,R} + R^{2} \nu \,D_{,RR} } \right]w_{,R} + \rho \,h\,w_{,tt} = 0, \\ \end{aligned}$$
(1)

where w is the transverse deflection, D the flexural rigidity and ν the Poisson’s ratio and a comma followed by a suffix denotes the partial derivative with respect to that variable.

For a harmonic solution, the deflection w can be expressed as

$$w(R,t) = W(R)e^{i{\omega} t} ,$$
(2)

where ω is the radian frequency. Equation (1) reduces to

$$\begin{aligned} & DW_{,RRRR} + \frac{2}{R}\left[ {D + R\,D_{,R} } \right]W_{,RRR} + \frac{1}{{R^{2} }}\left[ { - D + R(2 + \nu )\,D_{,R} + R^{2} D_{,RR} } \right]W_{,RR} \\ & \quad + \frac{1}{{R^{3} }}\left[ {D - R\,D_{,R} + R^{2} \nu \,D_{,RR} } \right]W_{,R} - \rho \,h\,\omega^{2} W = 0. \\ \end{aligned}$$
(3)

Assuming that the top and bottom surfaces of the plate are ceramic and metal-rich, respectively, for which the variations of the Young’s modulus E(z) and the density \(\rho (z)\) in the thickness direction are taken as

$$E(z) = (E_{c} - E_{m} )\left( {\frac{z}{h} + \frac{1}{2}} \right)^{g} + E_{m}$$
(4)
$$\rho (z) = (\rho_{c} - \rho_{m} )\left( {\frac{z}{h} + \frac{1}{2}} \right)^{g} + \rho_{m}$$
(5)

where \(E_{c}\), \(\rho_{c}\) and \(E_{m}\), \(\rho_{m}\) denote the Young’s modulus and the density of ceramic and metal constituents, respectively, and g is the volume fraction index.

The flexural rigidity and mass density are given as

$$D = \frac{1}{{1 - \nu^{2} }}\int\limits_{ - h/2}^{h/2} {E(z)} \,z^{2} dz$$
(6)
$$\rho = \frac{1}{h}\int\limits_{ - h/2}^{h/2} {\rho (z)} dz$$
(7)

Substituting Eqs. (4, 5) into Eqs. (6, 7), we obtain

$$D = \frac{{h^{3} }}{{1 - \nu^{2} }}\left[ {(E_{c} - E_{m} )\frac{{g^{2} + g + 2}}{4(g + 1)(g + 2)(g + 3)} + \frac{{E_{m} }}{12}} \right]$$
(8)
$$\rho = \frac{{\rho_{c} + \rho_{m} \,g}}{g + 1}\,$$
(9)

Introducing the non-dimensional variables \(r = {R \mathord{\left/ {\vphantom {R a}} \right. \kern-0pt} a},f = {W \mathord{\left/ {\vphantom {W a}} \right. \kern-0pt} a},\bar{h} = {h \mathord{\left/ {\vphantom {h a}} \right. \kern-0pt} a}\), Eq. (3) now reduces to

$$\begin{aligned} & D\,f_{,rrrr} + \frac{2}{r}\left[ {D + r\,D_{,r} } \right]f_{,rrr} + \frac{1}{{r^{2} }}\left[ { - D + r(2 + \nu )D_{,r} + r^{2} D_{,rr} } \right]f_{,rr} \\ & \quad + \frac{1}{{r^{3} }}\left[ {D - r\,D_{,r} + r^{2} \nu \,D_{,rr} } \right]f_{,r} = \rho \,a^{4} \omega^{2} f\,\bar{h} \\ \end{aligned}$$
(10)

Assuming the linear variation in the thickness, i.e. \(\bar{h} = h_{0} \left( {1 - \gamma \,r} \right),\gamma\) being the taper parameter and \(h_{0}\) is the non-dimensional thickness of the plate at the centre. Substituting the values of D and ρ from Eqs. (8, 9) into Eq. (10), we get

$$\begin{aligned} & r^{3} \left( {1 - \gamma \,r} \right)^{3} B\,f_{,rrrr} + 2\,r^{2} \left( {\left( {1 - \gamma \,r} \right)^{3} - 3\,\gamma \,r\left( {1 - \gamma \,r} \right)^{2} } \right)B\,f_{,rrr} \\ & \quad + r\,B\left( { - \left( {1 - \gamma \,r} \right)^{3} - 3\,\gamma \,r\left( {2 + \nu } \right)\left( {1 - \gamma \,r} \right)^{2} + 6\,r^{2} \alpha^{2} \left( {1 - \gamma \,r} \right)} \right)f_{,rr} \\ & \quad + B\,\left( {\left( {1 - \gamma \,r} \right)^{3} + 3r\,\alpha \left( {1 - \gamma \,r} \right)^{2} } \right)f_{,r} = r^{3}\Omega ^{2} A\left( {1 - \gamma \,r} \right)f \\ \end{aligned}$$
(11)

where

$$\begin{aligned} D & = D^{*} B\,(1 - \gamma \,r)^{3} a^{3} ,\quad\Omega ^{2} = \frac{{\rho_{c} h_{0} a^{4} }}{{D^{*} }}\omega^{2} ,\,D^{*} = \frac{{E_{c} h_{0}^{3} }}{{12(1 - \nu^{2} )}}, \\ A & = \left( {\frac{{\rho_{c} + \rho_{m} g}}{{\rho_{c} (g + 1)}}} \right),\quad B = \left[ {3\,\left( {1 - \frac{{E_{m} }}{{E_{c} }}} \right)\frac{{g^{2} + g + 2}}{(g + 1)(g + 2)(g + 3)} + \frac{{E_{m} }}{{E_{c} }}} \right] \\ \end{aligned}$$

Equation (11) is a fourth-order differential equation with variable coefficients whose exact solution is not possible. The approximate solution with appropriate boundary and regularity conditions has been obtained employing differential transform method.

2.1 Boundary Conditions: Clamped Edge

$$f(1) = 0,\,\,\,\frac{df}{dr}|_{r = 1} = 0$$
(12)

Regularity conditions at the centre (r = 0) of the plate-

$$\frac{df}{dr}|_{r = 0} = 0,Q_{r} |_{r = 0} = \left[ {D\left( {\frac{{d^{3} f}}{{d\,r^{3} }} + \frac{1}{r}\frac{{d^{2} f}}{{d\,r^{2} }} - \frac{1}{{r^{2} }}\frac{df}{dr}} \right) + D_{,r} \left( {\frac{{d^{2} f}}{{d\,r^{2} }} + \frac{\nu }{r}\frac{df}{dr}} \right)} \right]_{r = 0} = 0$$
(13)

where \(Q_{r}\) the radial shear force.

3 Method of Solution: Differential Transform Method

Following the description of the method given in Ref. [11], the transformed form of the governing differential Eq. (11) around \(r_{0} = 0\) will be written as

$$\begin{aligned} F_{k + 1} & = \frac{1}{{\left( {k^{2} - 1} \right)^{2} }}\cdot\,[3\,\gamma \,k(k - 1)\left( {k^{2} - k - 1 + \nu } \right)\,F_{k} \\ & \quad + \{ 3\,\gamma \,(k - 4)(k - 3)(k - 2)(k - 1) - 6\,\nu \,\gamma^{2} (k - 2)(k - 1) \\ & \quad - 3\gamma^{2} (k - 1)\left( {6\,k^{2} - 25\,k + 2\,\nu k - 2\,\nu } \right)\} \,F_{k - 1} \\ & \quad + \gamma^{3} (k - 2)\{ k^{3} - 4k^{2} + (2 + 3\nu )k - 3\,\nu + 1\} F_{k - 2} \\ & \quad + \frac{{\Omega ^{2} A}}{B}F_{k - 3} - \gamma \,\Omega ^{2} \frac{A}{B}F_{k - 4} ] \\ \end{aligned}$$
(14)

The transformed form of boundary and regularity conditions will be

$$Clamped\,edge\,condition:\sum\limits_{k\, = \,\,0}^{n} {F_{k} = 0} ,\sum\limits_{k\, = \,\,0}^{n} {k\,F_{k} = 0}$$
(15)
$$Regularity\,condition:F_{1} = 0,F_{3} = \frac{2}{3}\gamma (1 + \nu )F_{2}$$
(16)

4 Frequency Equation

Now, applying the boundary condition and regularity condition (15, 16) on the resulted F k expressions (14), we get the following equations:

$$\begin{aligned}\Phi _{11}^{(m)} (\Omega )F_{0} +\Phi _{12}^{(m)} (\Omega )F_{2} & = 0 \\\Phi _{21}^{(m)} (\Omega )F_{0} +\Phi _{22}^{(m)} (\Omega )F_{2} & = 0 \\ \end{aligned}$$
(17)

where \(\Phi _{11}^{(m)}\), \(\Phi _{12}^{(m)}\), \(\Phi _{21}^{(m)}\) and \(\Phi _{22}^{(m)}\) are polynomials in Ω of degree m where m = 2n. Equation (17) can be expressed in matrix form as follows:

$$\left[ {\begin{array}{*{20}c} {\Phi _{11}^{(m)} (\Omega )} & {\Phi _{12}^{(m)} (\Omega )} \\ {\Phi _{21}^{(m)} (\Omega )} & {\Phi _{22}^{(m)} (\Omega )} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {F_{0} } \\ {F_{2} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right\}$$
(18)

For a non-trivial solution of Eq. (18), the frequency determinant must vanish and hence

$$\left| {\begin{array}{*{20}c} {\Phi _{11}^{(m)} (\Omega )} & {\Phi _{12}^{(m)} (\Omega )} \\ {\Phi _{21}^{(m)} (\Omega )} & {\Phi _{22}^{(m)} (\Omega )} \\ \end{array} } \right| = 0$$
(19)

5 Numerical Results and Discussion

The frequency Eq. (19) provides the values of the frequency parameter Ω. The lowest three roots of this equation have been obtained using MATLAB to investigate the influence of taper parameter γ and volume fraction index g on the frequency parameter Ω. In the present analysis, the values of Young’s modulus and density for aluminium as metal and alumina as ceramic constituents are taken from [11], as follows:

$$E_{m} = 70\,{\text{GPa}},\,\rho_{m} = 2{,}702\;{\text{kg/m}}^{ 3} \quad {\text{and}}\quad E_{c} = 380\,{\text{GPa}},\,\rho_{c} = 3{,}800\;{\text{kg/m}}^{ 3}$$

The variation in the values of Poisson’s ratio is assumed to be negligible all over the plate and its value is taken as ν = 0.3. From the literature, the values of parameters are taken as

$$\begin{aligned} {\text{Volume}}\,{\text{fraction}}\,{\text{index}}\,g & = 0, 1, 2, 3, 4, 5; \\ {\text{Taper}}\,{\text{parameter}}\,\gamma & = - 0. 5,\, - 0. 3, - 0. 1,\,0. 1,\,0. 3,\,0. 5. \\ \end{aligned}$$

In order to choose an appropriate value of the number of terms ‘n’, a computer program has been developed and run for various values of g and γ. The convergence of frequency parameter Ω for the first three modes of vibration for a specified plate taking g = 5, γ = −0.5 is shown in Table 1, as maximum deviations were observed for this data. The frequency parameter Ω converges with the increasing value of n. The value of n has been fixed as 18, as there was no further improvement in the values of Ω even at the fourth place of decimal.

Table 1 Convergence study for first three modes of vibration for g = 5, γ = −0.5
Full size table

Numerical results have been given in Tables 2 and 3 and presented in Figs. 2, 3 and 4. The effect of volume fraction index g on the frequency parameter Ω for three different values of taper parameter γ has been demonstrated in Fig. 2. It has been observed that the value of frequency parameter Ω decreases with the increasing values of g whatever be the value of taper parameter γ. The corresponding rate of decrease is higher for smaller values of g (< 2) as compared to the higher values of g (> 3). Further, it increases with the increase in the number of modes.

Table 2 Values of frequency parameter Ω
Full size table
Table 3 Comparison of frequency parameter Ω for g = 0, γ = 0
Full size table
Fig. 2
figure 2

Frequency parameter Ω versus volume fraction index g

Full size image
Fig. 3
figure 3

Frequency parameter Ω versus taper parameter γ

Full size image
Fig. 4
figure 4

First three mode shapes for g = 5, γ = −0.5

Full size image

To study the effect of taper parameter γ on the frequency parameter Ω, a graph has been plotted for two different values of volume fraction index g = 0, 5 in Fig. 3. It has been noticed that the frequency parameter Ω decreases as the plate becomes thinner and thinner towards the outer edge. This effect is more pronounced for isotropic plate (g = 0) as compared to FGM plate (g = 5) and increases with the increase in the number of modes. Three-dimensional mode shapes for a specified plate, i.e. g = 5, γ = −0.5 for the first three modes of vibration has been presented in Fig. 4. A comparison of frequency parameter Ω for an isotropic plate has been given in Table 3. A close agreement of the results shows the versatility of the present technique.

6 Conclusion

The effect of thickness variation has been studied on the axisymmetric vibrations of functionally graded clamped circular plate employing differential transform method. From the numerical results, the following conclusions can be made:

  • The frequency parameter decreases with the increasing values of volume fraction index. From this fact, it can be observed that the frequencies for an isotropic plate (g = 0) are higher than that for the corresponding FGM plate (g > 0) which shows the superiority of the FGM plates over isotropic plate.

  • The frequency parameter decreases with the increasing values of taper parameter, i.e. the frequency parameter increases as the plate become thicker and thicker towards the outer boundary of the plate.