Keywords

1 Introduction

In every supply chain model, maintaining of deteriorating inventories is a major issue for almost all business organizations. Most of the goods decay over time. In general, some products deteriorate in a certain fixed period of storage like seasonal goods fruits, vegetables, etc., but certain goods lose their potentiality when the time passes, such as electronic items, radioactive substances, etc. Certain inventories like highly volatile liquids as ethanol, gasoline, etc., undergo depletion due to evaporation, so that deterioration is one of the most influential factors that affect the decision related to production and inventory management. Each business organization considers it quite seriously. With regard to all these issues, deterioration function is of various types that may be constant and time dependent. In our production model, we consider Weibull distribution as a deterioration function. Weibull distribution is one of the most reliable deterioration functions because it presents a perfect view of deteriorating inventory level. Covert and Philip [1] established an inventory model for deteriorating items having variable rate of deterioration. In their model, they use two-parameter Weibull deterioration. Misra [2] also presents a production model with two-parameter Weibull deterioration to show inventory depletion. Choi and Hwang [3] present an optimization of product planning problem with continuously distributed time lags. Aggarwal and Bahari-Hashani [4] synchronized production policies for deteriorating items in a declining market. Pakkala and Achary [5] present a deterministic inventory model for deteriorating items with two warehouses and finite replenishment rate. Jong et al. [6] developed an EOQ inventory model with time-varying demand and Weibull deterioration with shortages. Wu [7] presented an EOQ inventory model for items with Weibull distribution deterioration, ramp type demand rate, and partial backlogging. Lee and Wu [8] formulate an EOQ model for items with Weibull distributed deterioration, shortages, and power demand pattern. Banerjee and Agrawal [9] analyzed a two-warehouse inventory model for items with three-parameter Weibull distribution deterioration, shortages, and linear trend in demand. Roy and Chaudhuri [10] scheduled a production inventory model under stock-dependent demand, Weibull distribution deterioration, and shortage. Begum et al. [11] worked on an EOQ model for varying items with Weibull distribution deterioration and price-dependent demand. Konstantaras and Skouri [12] dealt a note on a production inventory model under stock-dependent demand, Weibull distribution deterioration, and shortage. Shilpi et al. [13] introduced an EPQ model of ramp type demand with Weibull deterioration under inflation and finite horizon in crisp and fuzzy environment.

In any production model, demand is a reliable factor on which the whole working of inventory model depends. Most researchers assume that demand depends on time as well as other factors. Stock-dependent demand is another way to look at practical situations. Many of the factors affect demand on a serious mode, but stock affects it in the most powerful manner. It may influence the production directly or indirectly, such as low stock raises the price of commodity in the market which decreases the demand and, if the stock level increases, then the price goes down and as a result demand increases. Therefore, it is observed that the stock level affects the demand in many ways. For example, if there are a large pile of goods available in the stock then the vendor announces a large discount to clear the stock. Many practitioners and researchers have analyzed this issue very seriously. Many researchers consider this as a realistic assumption, such as Datta et al. [14], Balki and Benkherouf [15], Teng and Chang [16], Wu et al. [17], Singh et al. [18], Singh and Singh [19], and finally, Sarker and Sarkar [20], Yang [21].

Customer return is also one of the most important factors that affect the production model. Customer returns are the products that may be returned by the customer after purchase. Customer may return these products due to several reasons such as defect in the product, customer is not satisfied with the product, some money-back guarantee, or maybe to replace the product, etc. Nowadays, customer returns occur in many different ways. Many researchers working in the stream like Hess and Mayhew [22] proposed a return of modeling merchandise in direct marketing. It is useful for the future studies of many researchers. Pasterneck [23] proposed a model for return policies of deteriorating items. In the same field, Anderson et al. [24] developed a relation between return and demand. Further, Ahmed et al. [25] introduced an inventory model for production as well as remanufacturing for quality and price-dependent return rate. In the same field, Hani et al. [26] derived an advertising policy customer’s disadoption and subscriber services cost learning. Now Jiang and Chan [27] establish a lot of sizing polices for expiry date deteriorating items and partial trade credit risk customers.

In this proposed model, we considered a production inventory model with shortage, partial backlogging, and customer returns. Two-parameter Weibull deterioration is considered here. In this model, production is dependent on demand and demand depends on stock and price. Customer return is a function of price, quantity sold, and inventory level. To match the illustrated model with realistic situations, we discussed three cases of Weibull deterioration as constant, linear, and quadratic. To illustrate the model utility numerical example, sensitivity analysis, and concavity of the profit functions are shown here.

2 Notations and Assumptions

2.1 Notations

c h :

Holding cost per unit per unit time

c d :

Deterioration cost per unit per unit time

c l :

Cost of lost sale per unit

p :

Selling price per unit, where p > c

θ :

Two-parameter Weibull deterioration rate

Q :

Order quantity

T :

Length of replenishment cycle time

B :

Backlogging rate

P :

Production rate

SV:

Salvage value per unit item

A :

Setup cost

I 1(t):

Inventory level at the time \( t \in [0, t_{1} ] \)

I 2(t):

Inventory level at the time \( t \in [t_{1} , t_{2} ] \)

I 3(t):

Inventory level at the time \( t \in [t_{2} , t_{3} ] \)

I 4(t):

Inventory level at the time \( t \in [t_{3} , t_{4} ] \)

2.2 Assumptions

  1. 1.

    Two-parameter Weibull distribution deterioration is considered here. \( \theta = \alpha \beta t^{\beta - 1} \).

  2. 2.

    Time horizon is finite.

  3. 3.

    The demand rate is \( D\left( {p,t} \right) = \left( {a - {\text{bp}} + {\text{cI}}\left( t \right)} \right) \) (where a > 0, b > 0) is a linearly decreasing function of the price but for the shortage and partial backlogging period demand depends on price only.

  4. 4.

    Shortage is allowed. The unsatisfied demand is backlogged, and the fraction of shortage back ordered is B, (B > 0), and 0 ≤ B ≤ 1.

  5. 4.

    We assume that the customer returns increase with both the quantity sold and price using the following general form: \( R\left( {p,t} \right) = {\text{AD}}\left( {p,t,I\left( t \right)} \right) + {\text{Bp}}\left( {B \ge 0,0 \le A < 1} \right). \)

  6. 5.

    Production is demand dependent, where P(t) = KD(t).

3 Model Formulation

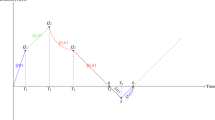
For the mathematical formulation of presented model, we solve the different inventory level as well as different costs. Firs, we can see that production starts when t = 0 then the inventory level goes up, but at the same time inventory goes down due to demand and deterioration. After time t 1, inventory decreases due to demand and deterioration. At the time interval t 2 < t < t 3, shortage occurs and the inventory level becomes negative and at the same time backlogging starts. In the fourth phase, production again starts and the backlogged demands get fulfilled partially.

$$ \frac{{{\text{d}}I_{1} (t)}}{{{\text{d}}t}} = P - D(p,t,I(t)) - \theta I_{1} (t),\quad I_{1} (0) = 0,\quad 0 \le t \le t_{1} $$
(1)
$$ \frac{{{\text{d}}I_{2} (t)}}{{{\text{d}}t}} = - D(p,t,I(t)) - \theta I_{2} (t),\quad I_{2} (t_{2} ) = 0,\quad t_{1} \le t \le t_{2} $$
(2)
$$ \frac{{{\text{d}}I_{3} (t)}}{{{\text{d}}t}} = - D(p)B,\quad I_{3} (t_{2} ) = 0,\quad t_{2} \le t \le t_{3} $$
(3)
$$ \frac{{{\text{d}}I_{4} (t)}}{{{\text{d}}t}} = P - D(p),\quad I_{1} \left( {t_{4} } \right) = 0,\quad t_{3} \le t \le t_{4} $$
(4)

As we see in Fig. 1.

Now solving the above equations, we get

$$ \begin{aligned} I_{1} (t) = (1 - k)(a - {\text{bp}}) & \left\{ {t + \frac{{\alpha t^{\beta + 1} }}{\beta + 1} - \frac{{c(k - 1)t^{2} }}{2} + c(k - 1)t^{2} + \frac{{\alpha c(k - 1)t^{\beta + 1} }}{\beta + 1}} \right. \\ & \left. {\, + \frac{{c^{2} (k - 1)^{2} t^{2} }}{2} - \alpha t^{\beta + 1} - \frac{{ \alpha^{2} t^{2\beta + 1} }}{\beta + 1} + \frac{{c\alpha (k - 1)t^{\beta + 2} }}{2}} \right\} \\ \end{aligned} $$
(5)
$$ I_{2} (t) = (1 - {\text{ct}} - \alpha t^{\beta } )\left\{ {(a - {\text{bp}})\left[ {(t_{2} - t) + \frac{c}{2}(t_{2}^{2} - t^{2} ) + \frac{\alpha }{\beta + 1} \left(t_{2}^{\beta + 1} - t^{\beta + 1} \right)} \right]} \right\} $$
(6)
$$ I_{3} (t) = - B(a - {\text{bp}})(t_{2} - t) $$
(7)
$$ I_{4} (t) = (k - 1)(a - {\text{bp}})(t - t_{4} ) $$
(8)

Now using the above equations, we can find the following cost:

Fig. 1
figure 1

Inventory level at time t

Full size image

The deterioration cost for the period (0, t 2 )

$$ = \theta c_{d} \left[ {\mathop \smallint \limits_{0}^{{t_{1} }} I_{1} (t){\text{d}}t + \mathop \smallint \limits_{{t_{1} }}^{{t_{2} }} I_{2} (t){\text{d}}t} \right] $$
(9)
$$ \begin{aligned} = & \,C_{d} \alpha \beta t^{\beta - 1} \left\{ {\left[ {\frac{{t_{1}^{2} }}{2} + \frac{{\alpha t_{1}^{\beta + 2} }}{{\left( {\beta + 1} \right)(\beta + 2)}} - \frac{{c(k - 1)t_{1}^{3} }}{6} + \frac{{c(k - 1)t_{1}^{3} }}{3}} \right.} \right. \\ & + \,\frac{{\alpha c(k - 1)t_{1}^{\beta + 2} }}{(\beta + 3)(\beta + 2)} + \frac{{c^{2} (k - 1)^{2} t_{1}^{4} }}{8} - \frac{{\alpha t_{1}^{\beta + 2} }}{(\beta + 2)}\,\left. { - \frac{{\alpha^{2} t^{2\, (\beta + 1)}}}{{\left( {\beta + 1} \right)(\beta + 2)}} + \frac{{c\alpha (k - 1)t^{(\beta + 3)} }}{2(\beta + 3)}} \right] \\ & + \,(a - bp)\left[ {t_{2} \left( {t_{2} - t_{1} } \right) - \left( {\frac{{t_{2}^{2} }}{2} - \frac{{t_{1}^{2} }}{2}} \right) + \frac{c}{2}\left( {t_{2}^{2} \left( {t_{2} - t_{1} } \right)} \right.} \right. \\ & \left. { - \,\left( {\frac{{t_{2}^{3} }}{3} - \frac{{t_{1}^{3} }}{3}} \right)} \right) + \frac{\alpha }{\beta + 1}\left( {t_{2}^{(\beta + 1)} (t_{2} - t_{1} ) - \left( {\frac{{t_{2}^{\beta + 2} }}{\beta + 2} - \frac{{t_{1}^{\beta + 2} }}{\beta + 2}} \right)} \right) \\ & - \,c\left( {t_{2} \left( {\frac{{t_{2}^{2} }}{2} - \frac{{t_{1}^{2} }}{2}} \right) - \left( {\frac{{t_{2}^{3} }}{3} - \frac{{t_{1}^{3} }}{3}} \right) + \frac{c}{2}\left( {t_{2}^{2} \left( {\frac{{t_{2}^{2} }}{2} - \frac{{t_{1}^{2} }}{2}} \right) - \left( {\frac{{t_{2}^{4} }}{4} - \frac{{t_{1}^{4} }}{4}} \right)} \right)} \right. \\ & \left. { + \,\frac{\alpha }{\beta + 1}\left( {t_{2}^{\beta + 1} \left( {\frac{{t_{2}^{2} }}{2} - \frac{{t_{1}^{2} }}{2}} \right) - \left( {\frac{{t_{2}^{\beta + 3} }}{\beta + 3} - \frac{{t_{1}^{\beta + 3} }}{\beta + 3}} \right)} \right)} \right) \\ & - \,\alpha \left( {\left( {t_{2} \left( {\frac{{t_{2}^{\beta + 2} }}{\beta + 2} - \frac{{t_{1}^{\beta + 2} }}{\beta + 2}} \right) - \left( {\frac{{t_{2}^{\beta + 2} }}{\beta + 2} - \frac{{t_{1}^{\beta + 2} }}{\beta + 2}} \right)} \right)} \right. \\ & + \,\frac{c}{2}\left( {t_{2}^{2} \left( {\frac{{t_{2}^{\beta + 2} }}{\beta + 2} - \frac{{t_{1}^{\beta + 2} }}{\beta + 2}} \right) - \left( {\frac{{t_{2}^{\beta + 3} }}{\beta + 3} - \frac{{t_{1}^{\beta + 3} }}{\beta + 3}} \right)} \right) \\ & \left. {\left. { + \,\frac{\alpha }{\beta + 1}\left( {t_{2}^{\beta + 1} \left( {\frac{{t_{2}^{\beta + 1} }}{\beta + 1} - \frac{{t_{1}^{\beta + 1} }}{\beta + 1}} \right) - \left( {\frac{{t_{2}^{2(\beta + 2)} }}{2(\beta + 1)} - \frac{{t_{1}^{2(\beta + 2)} }}{\beta + 3}} \right)} \right)} \right)} \right] \\ \end{aligned} $$
(10)

Holding cost for the inventory

$$ \begin{aligned} = & \,c_{h} \left[ {\mathop \smallint \limits_{0}^{{t_{1} }} I_{1} (t){\text{d}}t + \mathop \smallint \limits_{{t_{1} }}^{{t_{2} }} I_{2} (t){\text{d}}t} \right] \\ = & \,C_{h} \left\{ {(1 - k)(a - {\text{bp}})\left[ {\frac{{t_{1}^{2} }}{2} + \frac{{\alpha t_{1}^{\beta + 2} }}{(\beta + 1)(\beta + 2)} - \frac{{c(k - 1)t_{1}^{3} }}{6} + \frac{{c(k - 1)t_{1}^{3} }}{3}} \right.} \right. \\ & \left. { + \,\frac{{\alpha c(k - 1)t_{1}^{\beta + 2} }}{(\beta + 3)(\beta + 2)} + \frac{{c^{2} (k - 1)^{2} t_{1}^{4} }}{8} - \frac{{\alpha t_{1}^{\beta + 2} }}{(\beta + 2)} - \frac{{\alpha^{2} t^{2(\beta + 1)} }}{(\beta + 1)(\beta + 2)} + \frac{{c\alpha (k - 1)t^{(\beta + 3)} }}{2(\beta + 3)}} \right] \\ & + \,(a - {\text{bp}})\left[ {t_{2} (t_{2} - t_{1} ) - \left( {\frac{{t_{2}^{2} }}{2} - \frac{{t_{1}^{2} }}{2}} \right)} \right. \\ & + \,\frac{c}{2}\left( {t_{2}^{2} (t_{2} - t_{1} ) - \left( {\frac{{t_{2}^{3} }}{3} - \frac{{t_{1}^{3} }}{3}} \right)} \right) + \frac{\alpha }{\beta + 1}\left( {t_{2}^{(\beta + 1)} (t_{2} - t_{1} ) - \left( {\frac{{t_{2}^{\beta + 2} }}{\beta + 2} - \frac{{t_{1}^{\beta + 2} }}{\beta + 2}} \right)} \right) \\ & - \,c\left( {t_{2} \left( {\frac{{t_{2}^{2} }}{2} - \frac{{t_{1}^{2} }}{2}} \right) - \left( {\frac{{t_{2}^{3} }}{3} - \frac{{t_{1}^{3} }}{3}} \right) + \frac{c}{2}\left( {t_{2}^{2} \left( {\frac{{t_{2}^{2} }}{2} - \frac{{t_{1}^{2} }}{2}} \right) - \left( {\frac{{t_{2}^{4} }}{4} - \frac{{t_{1}^{4} }}{4}} \right)} \right)} \right. \\ & \left. { + \,\frac{\alpha }{\beta + 1}\left( {t_{2}^{\beta + 1} \left( {\frac{{t_{2}^{2} }}{2} - \frac{{t_{1}^{2} }}{2}} \right) - \left( {\frac{{t_{2}^{\beta + 3} }}{\beta + 3} - \frac{{t_{1}^{\beta + 3} }}{\beta + 3}} \right)} \right)} \right) \\ & - \,\alpha \left( {\left( {t_{2} \left( {\frac{{t_{2}^{\beta + 2} }}{\beta + 2} - \frac{{t_{1}^{\beta + 2} }}{\beta + 2}} \right)} \right.} \right. \\ & \left. { - \,\left( {\frac{{t_{2}^{\beta + 2} }}{\beta + 2} - \frac{{t_{1}^{\beta + 2} }}{\beta + 2}} \right)} \right) + \frac{c}{2}\left( {t_{2}^{2} \left( {\frac{{t_{2}^{\beta + 2} }}{\beta + 2} - \frac{{t_{1}^{\beta + 2} }}{\beta + 2}} \right) - \left( {\frac{{t_{2}^{\beta + 3} }}{\beta + 3} - \frac{{t_{1}^{\beta + 3} }}{\beta + 3}} \right)} \right) \\ & \left. {\left. {\left. { + \,\frac{\alpha }{\beta + 1}\left( {t_{2}^{\beta + 1} \left( {\frac{{t_{2}^{\beta + 1} }}{\beta + 1} - \frac{{t_{1}^{\beta + 1} }}{\beta + 1}} \right) - \left( {\frac{{t_{2}^{2(\beta + 2)} }}{2(\beta + 1)} - \frac{{t_{1}^{2(\beta + 2)} }}{\beta + 3}} \right)} \right)} \right)} \right]} \right\} \\ \end{aligned} $$
(11)

Return cost for the inventory

$$ \begin{aligned} & (p - {\text{SV}})\left\{ {A(a - {\text{bp}})t_{2} + Ac} \right.\left[ {\frac{{t_{1}^{2} }}{2} + \frac{{\alpha t_{1}^{\beta + 2} }}{(\beta + 1)(\beta + 2)} - \frac{{c(k - 1)t_{1}^{3} }}{6} + \frac{{c(k - 1)t_{1}^{3} }}{3}} \right. \\ & \quad \left. { + \,\frac{{\alpha c(k - 1)t_{1}^{\beta + 2} }}{(\beta + 3)(\beta + 2)} + \frac{{c^{2} (k - 1)^{2} t_{1}^{4} }}{8} - \frac{{\alpha t_{1}^{\beta + 2} }}{(\beta + 2)} - \frac{{\alpha^{2} t^{2(\beta + 1)} }}{(\beta + 1)(\beta + 2)} + \frac{{c\alpha (k - 1)t^{(\beta + 3)} }}{2(\beta + 3)}} \right] \\ & \quad + \,{\text{Ac}}(a - {\text{bp}})\left[ {t_{2} (t_{2} - t_{1} ) - \left( {\frac{{t_{2}^{2} }}{2} - \frac{{t_{1}^{2} }}{2}} \right)} \right. + \frac{c}{2}\left( {t_{2}^{2} (t_{2} - t_{1} ) - \left( {\frac{{t_{2}^{3} }}{3} - \frac{{t_{1}^{3} }}{3}} \right)} \right) \\ & \quad + \,\frac{\alpha }{\beta + 1}\left( {t_{2}^{(\beta + 1)} (t_{2} - t_{1} ) - \left( {\frac{{t_{2}^{\beta + 2} }}{\beta + 2} - \frac{{t_{1}^{\beta + 2} }}{\beta + 2}} \right)} \right) - c\left( {t_{2} \left( {\frac{{t_{2}^{2} }}{2} - \frac{{t_{1}^{2} }}{2}} \right) - \left( {\frac{{t_{2}^{3} }}{3} - \frac{{t_{1}^{3} }}{3}} \right)} \right. \\ & \quad \left. { + \,\frac{c}{2}\left( {t_{2}^{2} \left( {\frac{{t_{2}^{2} }}{2} - \frac{{t_{1}^{2} }}{2}} \right) - \left( {\frac{{t_{2}^{4} }}{4} - \frac{{t_{1}^{4} }}{4}} \right)} \right) + \frac{\alpha }{\beta + 1}\left( {t_{2}^{\beta + 1} \left( {\frac{{t_{2}^{2} }}{2} - \frac{{t_{1}^{2} }}{2}} \right) - \left( {\frac{{t_{2}^{\beta + 3} }}{\beta + 3} - \frac{{t_{1}^{\beta + 3} }}{\beta + 3}} \right)} \right)} \right) \\ & \quad - \,\alpha \left( {\left( {t_{2} \left( {\frac{{t_{2}^{\beta + 2} }}{\beta + 2} - \frac{{t_{1}^{\beta + 2} }}{\beta + 2}} \right) - \left( {\frac{{t_{2}^{\beta + 2} }}{\beta + 2} - \frac{{t_{1}^{\beta + 2} }}{\beta + 2}} \right)} \right)} \right. \\ & \quad + \,\frac{c}{2}\left( {t_{2}^{2} \left( {\frac{{t_{2}^{\beta + 2} }}{\beta + 2} - \frac{{t_{1}^{\beta + 2} }}{\beta + 2}} \right) - \left( {\frac{{t_{2}^{\beta + 3} }}{\beta + 3} - \frac{{t_{1}^{\beta + 3} }}{\beta + 3}} \right)} \right) \\ & \quad \left. {\left. {\left. { + \,\frac{\alpha }{\beta + 1}\left( {t_{2}^{\beta + 1} \left( {\frac{{t_{2}^{\beta + 1} }}{\beta + 1} - \frac{{t_{1}^{\beta + 1} }}{\beta + 1}} \right) - \left( {\frac{{t_{2}^{2(\beta + 2)} }}{2(\beta + 1)} - \frac{{t_{1}^{2(\beta + 2)} }}{\beta + 3}} \right)} \right)} \right)} \right] + {\text{Bpt}}_{2} } \right\} \\ \end{aligned} $$
(12)

Lost sale cost for the inventory

$$ = c_{l} \mathop \smallint \limits_{{t_{2} }}^{{t_{3} }} (1 - B){\text{Ddt}} = c_{l} (1 - B)\left\{ {(a - {\text{bp}})(t_{3} - t_{2} )} \right\} $$
(13)

Production cost for the inventory

$$ \begin{aligned} = & \,c_{p} \left[ {\mathop \smallint \limits_{0}^{{t_{1} }} {\text{Pdt}} + \mathop \smallint \limits_{{t_{3} }}^{{t_{4} }} {\text{Pdt}}} \right] \\ = & \,c_{p} \left\{ {k(a - {\text{bp}})t_{1} + ck\left[ {\frac{{t_{1}^{2} }}{2} + \frac{{\alpha t_{1}^{\beta + 2} }}{(\beta + 1)(\beta + 2)} - \frac{{c(k - 1)t_{1}^{3} }}{6} + \frac{{c(k - 1)t_{1}^{3} }}{3}} \right.} \right. \\ & \left. { + \,\frac{{\alpha c(k - 1)t_{1}^{\beta + 2} }}{(\beta + 3)(\beta + 2)} + \frac{{c^{2} (k - 1)^{2} t_{1}^{4} }}{8} - \frac{{\alpha t_{1}^{\beta + 2} }}{(\beta + 2)} - \frac{{\alpha^{2} t^{2(\beta + 1)} }}{(\beta + 1)(\beta + 2)} + \frac{{c\alpha (k - 1)t^{(\beta + 3)} }}{2(\beta + 3)}} \right] \\ & + \,k(a - {\text{bp}})(t_{4} - t_{2} ) + {\text{ck}}\left[ { - B(a - {\text{bp}})(t_{2} (t_{4} - t_{2} ) - \left( {\frac{{t_{4}^{2} }}{2} - \frac{{t_{2}^{2} }}{2}} \right)} \right. \\ & \left. {\left. { + \,(k - 1)(a - {\text{bp}})\left( {\frac{{t_{4}^{2} }}{2} - \frac{{t_{2}^{2} }}{2} - t_{4} (t_{4} - t_{2} )} \right)} \right]} \right\} \\ \end{aligned} $$
(14)

Sales revenue for the inventory

$$ \begin{aligned} = & \,p\left\{ {\left( {(a - {\text{bp}})(t_{1} + t_{2} + B(t_{4} - t_{1} ))} \right) + c\left[ {\frac{{t_{1}^{2} }}{2} + \frac{{\alpha t_{1}^{\beta + 2} }}{(\beta + 1)(\beta + 2)} - \frac{{c(k - 1)t_{1}^{3} }}{6}} \right.} \right. \\ & + \,\frac{{c(k - 1)t_{1}^{3} }}{3} + \frac{{\alpha c(k - 1)t_{1}^{\beta + 2} }}{(\beta + 3)(\beta + 2)} + \frac{{c^{2} (k - 1)^{2} t_{1}^{4} }}{8} - \frac{{\alpha t_{1}^{\beta + 2} }}{(\beta + 2)} - \frac{{\alpha^{2} t^{2(\beta + 1)} }}{(\beta + 1)(\beta + 2)} \\ & \left. { + \,\frac{{c\alpha (k - 1)t^{(\beta + 3)} }}{2(\beta + 3)}} \right] + c(1 + B)(a - {\text{bp}})\left[ {t_{2} (t_{2} - t_{1} ) - \left( {\frac{{t_{2}^{2} }}{2} - \frac{{t_{1}^{2} }}{2}} \right)} \right. \\ & + \,\frac{c}{2}\left( {t_{2}^{2} (t_{2} - t_{1} ) - \left( {\frac{{t_{2}^{3} }}{3} - \frac{{t_{1}^{3} }}{3}} \right)} \right) + \frac{\alpha }{\beta + 1}\left( {t_{2}^{(\beta + 1)} (t_{2} - t_{1} ) - \left( {\frac{{t_{2}^{\beta + 2} }}{\beta + 2} - \frac{{t_{1}^{\beta + 2} }}{\beta + 2}} \right)} \right) \\ & - \,c\left( {t_{2} \left( {\frac{{t_{2}^{2} }}{2} - \frac{{t_{1}^{2} }}{2}} \right) - \left( {\frac{{t_{2}^{3} }}{3} - \frac{{t_{1}^{3} }}{3}} \right) + \frac{c}{2}\left( {t_{2}^{2} \left( {\frac{{t_{2}^{2} }}{2} - \frac{{t_{1}^{2} }}{2}} \right) - \left( {\frac{{t_{2}^{4} }}{4} - \frac{{t_{1}^{4} }}{4}} \right)} \right)} \right. \\ & \left. { + \,\frac{\alpha }{\beta + 1}\left( {t_{2}^{\beta + 1} \left( {\frac{{t_{2}^{2} }}{2} - \frac{{t_{1}^{2} }}{2}} \right) - \left( {\frac{{t_{2}^{\beta + 3} }}{\beta + 3} - \frac{{t_{1}^{\beta + 3} }}{\beta + 3}} \right)} \right)} \right) \\ & - \,\alpha \left( {\left( {t_{2} \left( {\frac{{t_{2}^{\beta + 2} }}{\beta + 2} - \frac{{t_{1}^{\beta + 2} }}{\beta + 2}} \right) - \left( {\frac{{t_{2}^{\beta + 2} }}{\beta + 2} - \frac{{t_{1}^{\beta + 2} }}{\beta + 2}} \right)} \right)} \right. \\ & + \,\frac{c}{2}\left( {t_{2}^{2} \left( {\frac{{t_{2}^{\beta + 2} }}{\beta + 2} - \frac{{t_{1}^{\beta + 2} }}{\beta + 2}} \right) - \left( {\frac{{t_{2}^{\beta + 3} }}{\beta + 3} - \frac{{t_{1}^{\beta + 3} }}{\beta + 3}} \right)} \right) \\ & \left. {\left. { + \,\frac{\alpha }{\beta + 1}\left( {t_{2}^{\beta + 1} \left( {\frac{{t_{2}^{\beta + 1} }}{\beta + 1} - \frac{{t_{1}^{\beta + 1} }}{\beta + 1}} \right) - \left( {\frac{{t_{2}^{2(\beta + 2)} }}{2(\beta + 1)} - \frac{{t_{1}^{2(\beta + 2)} }}{\beta + 3}} \right)} \right)} \right)} \right] \\ & + \,{\text{Bc}}(a - {\text{bp}})\left[ {(t_{2} (t_{3} - t_{2} ) - \left( {\frac{{t_{3}^{2} }}{2} - \frac{{t_{2}^{2} }}{2}} \right))} \right] \\ & \left. { + \,{\text{Bc}}(a - {\text{bp}})\left[ {(k - 1)\left( {\frac{{t_{4}^{2} }}{2} - \frac{{t_{2}^{2} }}{2} - t_{4} (t_{4} - t_{2} )} \right)} \right]} \right\} \\ \end{aligned} $$
(15)

Shortage cost for the inventory

$$ \begin{aligned} & = c_{s} \left[ { - \mathop \smallint \limits_{{t_{2} }}^{{t_{3} }} I_{3} \left( t \right){\text{d}}t - \mathop \smallint \limits_{{t_{3} }}^{{t_{4} }} I_{4} \left( t \right){\text{d}}t} \right] \\ & = c_{s} \left\{ { - (a - {\text{bp}})B\left[ {\left( {t_{2} (t_{3} - t_{2} ) - \left( {\frac{{t_{3}^{2} }}{2} - \frac{{t_{2}^{2} }}{2}} \right)} \right)} \right] - (a - {\text{bp}})(k - 1)\left[ {\left( {\frac{{t_{4}^{2} }}{2} - \frac{{t_{3}^{2} }}{2} - t_{4} (t_{4} - t_{3} )} \right)} \right]} \right\} \\ \end{aligned} $$
(16)

4 Profit Function

PT = sales revenue (shortage cost–deterioration cost–production cost–lost sale cost–return cost–holding cost).

5 Numerical Example for All Three Cases

We use the following parameters to illustrate the numerical example for the described model.

a = 24; b = 0.2; c s  = 0.03; c h  = 0.3; c d  = 0.05; c l  = 0.03; c p  = 100; B = 0.001; A = 0.01; p = 110; P = 10; SV = 100; α = 0.005; k = 3;

To solve the numerical example for all the three deterioration cases, we use the software mathematica 7 and the optimal results are presented as follows:

  1. Case 1:

    When β = 1 the value of profit function and other variables is

    PT = 31921.6; t 1 = 12.436; t 3 = 59.4748.

  2. Case 2:

    When β = 2 the value of profit function and other variables is

    PT = 17560.4; t 1 = 5.64778; t 3 = 35.5941.

  3. Case 3:

    When β = 3 the value of profit function and other variables is

    PT = 3719.8; t 1 = 3.5438; t 3 = 9.72077.

6 Sensitivity Analysis for Different Parameters

To study the behavior of profit function w.r.t different parameter, see below.

Parameters

Change in values

When β = 1

When β = 2

When β = 3

TP

t 1

t 3

TP

t 1

t 3

TP

t 1

t 3

c h

0.3

31912.6

12.436

59.4748

17560.4

5.6477

35.5941

13055.5

3.84339

26.278

0.4

31931.1

12.439

59.4767

17561.3

5.6380

35.5810

13054.2

3.81433

26.2429

0.5

31904.6

12.4462

59.4785

17562.1

5.6294

35.5684

13053.0

3.78729

26.2101

0.4

31950.1

12.4453

59.4797

17563.0

5.6202

35.5563

13052.1

3.81433

26.1796

c

0.01

31912.6

12.436

59.4748

17560.4

5.6477

35.5941

13055.5

3.84339

26.278

0.02

17586.2

10.4011

35.2377

9196.28

5.1735

20.7431

6751.02

3.6896

15.1687

0.03

12577.4

9.2922

27.0972

6438.04

4.9260

15.8394

4701.31

3.5464

11.4945

0.04

9882.97

8.5089

23.0866

5092.38

4.8097

13.5562

3719.8

3.5438

9.7207

B

0.001

31912.6

12.436

59.4748

17560.4

5.6477

35.5941

13055.5

3.84339

26.278

0.002

31932.8

12.4364

59.4917

17564.0

5.6487

35.5997

13057.5

3.8444

26.2815

0.003

31944.0

12.4365

59.5074

17576.5

5.6497

35.6054

13059.5

3.8454

26.2849

0.004

31955.2

12.4368

59.528

17571.1

5.6508

35.6112

13061.4

3.8463

26.2881

c s

0.03

31912.6

12.436

59.4748

17560.4

5.6477

35.5941

13055.5

3.84339

26.278

0.04

31904.0

12.4364

59.4762

17560.1

5.6488

35.6073

13056.8

3.84431

26.289

0.05

31886.4

12.4365

59.4769

17559.8

5.6498

35.6207

13058.2

3.84499

26.301

0.06

31868.8

12.4367

59.4776

17559.6

5.6512

35.6343

13059.5

3.84621

26.312

θ

0.91

31912.6

12.436

59.4748

17560.4

5.6477

35.5941

13055.5

3.84339

26.278

0.92

31868.8

12.4366

59.4776

17560.2

5.6477

35.5940

13055.2

3.8431

26.276

0.93

31864.6

12.4368

59.4777

17560.1

5.6476

35.5938

13055.1

3.8429

26.274

0.94

31860.4

12.4369

59.4774

17559.4

5.6478

35.5936

13054.4

3.8428

26.272

7 Observations

In this paper, we discussed the three cases of Weibull deterioration where we considered the different values of β such as β = 1, β = 2, and β = 3 in case first, second, and third case, respectively. For all these cases the values of profit function and decision variable are different. Now, we see the effect of change of different parameters on profit function and decision variables.

  1. Case 1:

    When β = 1 (constant deterioration)

    1. I.

      If we increase the value of parameter c h the value of profit function is fluctuated up and down but the value of t 1 and t 3 increases regularly.

    2. II.

      If we increase the value of c the value of profit function t 1 and t 3 decreases continuously.

    3. III.

      If the value of B increases there is a continuous increase in the value of profit, as well as in t 1 and t 3.

    4. IV.

      When there is increase in the value of c s the profit function decreases but the value of t 1 and t 3 increases regularly.

    5. V.

      On increasing the value of θ, profit decreases but the value of t 1 and t 3 increases.

  2. Case 2:

    When β = 2 (linear deterioration)

    1. I.

      When we increase the value of c h the value of profit function increases but the value of t 1 and t 3 decreases.

    2. II.

      If we increase the value of c the value of profit as well as t 1 and t 3 decreases vastly.

    3. III.

      On increasing the value of B, value of profit function t 1 and t 3 increases simultaneously.

    4. IV.

      If we increase the value of c s the value of total profit decreases and the value of t 1 and t 3 increases.

    5. V.

      When we increase the value of θ the value of total profit and t 1 and t 3 decreases.

  3. Case 3:

    When β = 3 (quadratic deterioration)

    1. I.

      After increasing the value of c h , the values of TP, t 1, and t 3 decrease.

    2. II.

      On increasing the value of c again, the values of TP, t 1, and t 3 decrease regularly.

    3. III.

      When we increase the value of B the values of TP, t 1, and t 3 increase.

    4. IV.

      On increasing the value of c s the values of TP, t 1, and t 3 increase.

    5. V.

      When we increase the value of θ the values of TP, t 1, and t 3 decrease.

8 Concavity of Profit Functions for Different Cases

See Figs. 2, 3, and 4.

Fig. 2
figure 2

Concavity of graph function for constant deterioration

Full size image
Fig. 3
figure 3

Concavity of graph function for linear deterioration

Full size image
Fig. 4
figure 4

Concavity of graph function for quadratic deterioration

Full size image

9 Conclusion

In this paper, we worked on an economic production model having two-parameter Weibull deterioration. Demand is considered as a function of stock, price, and time but demand for shortage period depends only on price. Production also depends on demand. Shortage is allowed and is partially backlogged. To frame this model in real-life situations, we also considered customer return as a factor of quantity sold, price, and inventory level. As we know that in a realistic situation, deterioration may differ with time, so to be more practical, we consider three types of Weibull deterioration rates. We considered three cases in which deterioration rate is constant, linear, and quadratic. By sensitivity analysis, the difference between concavity of graph and behavior of profit function is recognizable. We also compare these cases by numerical example, sensitivity analysis, and concavity of profit function.