Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

2.1 Introduction

Currently, most existing studies on the problem of interference mitigation, e.g., [1–10], have assumed that the interference channel gains are static. Based on such an ideal assumption, there are several nongame theoretic [1, 9] and game-theoretic [2–8, 10] interference mitigation approaches. However, the assumption of static channels is not true since they are always time-varying in practice, which is the inherent feature of wireless communications.

In this chapter, we consider a multiuser, multichannel opportunistic spectrum access network, where the users choose orthogonal channels to mitigate mutual interference [4, 5, 7–10]. The considered network is completed distributed, as there is no centralized controller and no information exchange among users. To address the time-varying nature of wireless communication, it is assumed that the channels undergo block-fading. Block-fading means that the channel gains remain unchanged in a slot but change randomly in the next slot, which is realistic and has been extensively used in the past literature.

Following the similar ideas proposed in [6, 9, 10], in which the weighted aggregate interference for static channels is minimized, the network utility in this chapter is naturally extended to the expected weighted aggregate interference for time-varying channels. As a result, the optimization objective is to find channel selection profiles that minimize this network utility in a distributed manner. Since the channel selections of the users are distributed and autonomous, we formulate the problem of opportunistic spectrum access as a noncooperative game. With the formulated game model, we then propose a stochastic automata-based distributed learning algorithm, which converges to pure strategy NE of the interference mitigation game in time-varying environment. Note that the main analysis and results in this chapter were presented in [11].

2.2 System Model and Problem Formulation

2.2.1 System Model

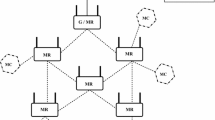
We consider a distributed canonical wireless network consisting of multiple autonomous users. Note that each user in canonical networks is not a single communication entity but a collection of multiple entities with intracommunications [12–14]. Generally, there is a leading entity choosing the operational channel and the belonged members share the channel using some multiple access control mechanisms, e.g., TDMA or CSMA/CA. Examples of wireless canonical network are given by, e.g., a WLAN access point with the serving clients [12] and a cluster head together with its members [9]. A comprehensive review on canonical networks can be found in [9]. An illustrative example of the considered canonical networks is shown in Fig. 2.1.

Fig. 2.1
figure 1

An illustrative example of canonical networks

Full size image

Suppose that there are N users and M channels, and each user chooses one channel for communication. Denote the user set as \(\mathbb {N}=\{1,\ldots ,N\}\) and the channel set as \(\mathbb {M}=\{1,\ldots ,M\}\). To capture the time-variation of channels, it is assumed that all the channels undergo block-fading, i.e., the channel gains are block-fixed in a time slot and change randomly in the next slot. Furthermore, each user chooses exactly one channel for intra-communication at a time. When two users, say m and n, choose a channel simultaneously, mutual interference emerges, the instantaneous interference gain from users m to n in a specific slot can be expressed as:

$$\begin{aligned} w^s_{mn} = (d_{mn})^{-\alpha }\varepsilon ^s_{mn}, \end{aligned}$$
(2.1)

where the superscript s denotes the selected channel, \(d_{mn}\) is the physical distance between m and n, \(\alpha \) is the path loss exponent, and \(\varepsilon ^s_{mn}\) is the instantaneous random component of the path loss [15], e.g., Rayleigh fading. Due to fading in wireless environment, the instantaneous random components between two users in each slot are generally different. However, their expected values are assumed to be the same. Therefore, we can denote the expected value of the random components between any two users on a channel as \(\bar{\varepsilon }^s_{mn}={\mathbf{E }}[\varepsilon ^s_{mn}]={\mathbf{E }}[\varepsilon ^s_{nm}]\), \(\forall m,n \in \mathbb {N}\), \(\forall s\in \mathbb {M}\).

Remark 2.1

The interference channel model characterized by (5.2) is very general, since the instantaneous random components \(\varepsilon ^s_{mn}\) can vary from slot to slot, from channel to channel, and from user to user. Furthermore, the dynamics may be independent or correlated. In addition, the expected value of random component \(\bar{\varepsilon }^s_{mn}\) can also vary from channel to channel and from user to user. Thus, the analysis and results obtained in this chapter suitable for several practical scenarios, and some examples are given by: (i) when it is unit-constant, i.e., \(\varepsilon ^s_{mn}=1, \forall m, n, s\), it corresponds to a scenario where only large-scale power-loss is considered, (ii) when it is log-normal distribution, it corresponds to the medium-scale power-loss, and (iii) when it is Rayleigh/Nakagami distribution, which means that multiple-path power-loss is considered.

2.2.2 Problem Formulation

Denote the chosen channel of user n in a slot as \(a_n\), \(a_n \in \mathbb {M}\), then the instantaneous achievable rate of user n is given by:

$$\begin{aligned} R_n= B\log \Big (1+\frac{p_nw^{a_n}_{nn}}{BN_0+ I_n}\Big ), \end{aligned}$$
(2.2)

where B is the channel bandwidth, \(w^{a_n}_{nn}=(d_{nn})^{-\alpha }\varepsilon ^{a_n}_{nn}\) is the intracommunication channel gain of user n (the channel gain between the head and the serving clients), \(p_n\) is the transmitting power, \(N_0\) is the noise power spectrum density, and \(I_n\) is the aggregate interference experienced by user n. For an action selection profile of all the users \(a=\{a_1,\dots ,a_N\}\), \(I_n\) is random and can be expressed by:

$$\begin{aligned} I_n=\sum \limits _{m \in \mathbb {\{N} \backslash n\}} f(a_m,a_n) p_m w^{a_n}_{mn}, \end{aligned}$$
(2.3)

where \(X\backslash Y\) means that Y is excluded from the set X, and \(f(\cdot )\) is the following indicator function:

$$\begin{aligned} f(x,y) = \left\{ \begin{array}{l} 1,\;\;x=y \\ 0,\;\;x \ne y. \\ \end{array} \right. \end{aligned}$$
(2.4)

According to (2.2), the aggregate expected network rate achieved by all the users can be expressed as:

$$\begin{aligned} R^\mathrm{{sum}}=\sum \limits _{n \in \mathbb {N}} {\mathbf{E }}[R_n] \end{aligned}$$
(2.5)

From the perspective of interference mitigation, we consider the expected weighted aggregate interference in the network, which is defined as:

$$\begin{aligned} U=\sum \limits _{n \in \mathbb {N}} p_n {\mathbf{E }}[I_n]= \sum \limits _{n \in \mathbb {N}} \sum \limits _{m \in \mathbb {\{N} \backslash n\}} p_mp_n \bar{w}^{a_n}_{mn}f(a_m,a_n), \end{aligned}$$
(2.6)

where \(\bar{w}^{a_n}_{mn}={\mathbf{E }}[w^{a_n}_{mn}]=(d_{mn})^{-\alpha } \bar{\varepsilon }^{a_n}_{mn}\) is the expected interference gain from user m to user n in channel \(a_n\).

Note that the considered network utility metric, i.e., the weighted aggregate interference, has been studied in previous studies [6, 9, 10]. In [6], it was shown that such a network utility can balance the transmitting power and the experienced interference. Furthermore, it has been shown that with this network utility, near-optimal network rate can be achieved in low SINR regime [9]. Existing studies were mainly for static scenarios with fixed channel gains. In comparison, in order to address the random and instantaneous fading components, i.e., \(\varepsilon ^s_{mn}\), in wireless environment, we consider the expected version of weighted aggregate interference here. Therefore, motivated by the previous researches on interference mitigation rather than maximizing throughput directly, e.g., [4, 5, 9], the considered objective here is to minimize the expected weighted aggregate interference, as specified by (2.6), i.e.,

$$\begin{aligned} (P1:) \;\;\;\;a_{opt}\in \mathop {\arg }\limits _{a } {\min } \; U \end{aligned}$$
(2.7)

2.3 Interference Mitigation Game in Time-Varying Environment

As the decision variable (channel selection) is discrete, the interference mitigation problem P1 is a combinatorial optimization problem. On the condition that all the key parameters including \(p_n\), \(d_{mn}\) and \(\bar{\varepsilon }^s_{mn}\), \(\forall m,n\in \mathbb {N}, s\in \mathbb {M}\) are a priori known, centralized approaches can be applied. However, if there is no centralized control and these parameters are unknown, which is exactly the scenario considered in this chapter, the task of solving P1 is challenging. In the following, we propose a game-theoretic distributed approach in time-varying environment.

2.3.1 Game Model

The problem of distributed channel selection for interference mitigation in canonical networks is formulated as a noncooperative game. Formally, the game is denoted as \({G}_c=[\mathbb {N},{\{{{A}_n}\}_{n\in \mathbb {N}}},{\{{u_n}\}_{n\in \mathbb {N}}}]\), where \(\mathbb {N} = \{1,\ldots ,N\}\) is the player set, \(A_n=\{1,\ldots ,M\}\) is the available actions (channel) set for each player n, and \(u_n\) is the utility function of player n. As the experienced interference is a random variable in each slot, we consider the following utility function, which is defined as the expected experienced interference, i.e.,

$$\begin{aligned} \begin{array}{l} u_n(a_n,a_{-n})=D-p_n{\mathbf{E }}[I_n]=D-\sum \limits _{m \in \mathbb {\{N} \backslash n\}} p_np_m \bar{w}^{a_n}_{mn}f(a_m,a_n), \end{array} \end{aligned}$$
(2.8)

where \(a_{-n}\) is the channel selection profile of all the players except player n, \(I_n\) is the experienced interference of player n, as specified by (2.3), and D is a predefined positive constant which will be illustrated later. Then, the proposed interference mitigation game is expressed as:

$$\begin{aligned} ({G}): \;\;\;\;\;\; \mathop {\max }\limits _{a_n \in A_n} u_n(a_n,a_{-n}),\quad \forall n \in \mathbb {N}. \end{aligned}$$
(2.9)

2.3.2 Analysis of Nash Equilibrium

In the following, we analyze the Nash equilibrium (NE) of the formulated interference mitigation game and investigate its properties.

Theorem 2.1

The formulated interference mitigation game \(G_c\) is an exact potential game which has at least a pure strategy NE point, and the optimal channel selection that globally minimizes the expected weighted aggregate interference constitutes a pure strategy NE point of G.

Proof

Detailed lines for the proof are omitted here but can be found in [11]. In the following, only the proof skeleton is presented. First, we construct the following potential function:

$$\begin{aligned} \varPhi ({a_n},{a_{ - n}}) = -\frac{1}{2}\sum \limits _{n\in \mathbb {N}} \sum \limits _{m \in \mathbb {\{N} \backslash n\}} p_mp_n \bar{w}^{a_n}_{mn}f(a_m,a_n), \end{aligned}$$
(2.10)

which immediately yields the following equation:

$$\begin{aligned} \varPhi ({a_n},{a_{ - n}}) = -\frac{1}{2}U(a_n,a_{-n}), \end{aligned}$$
(2.11)

through which the network utility \(U(a_n,a_{-n})\), as specified by (2.6), is related to the potential function. Then, after some mathematical manipulations, it can be verified that the change in individual utility function caused by any player’s unilateral deviation is the same as that in the potential function. Thus, according to the definition given in Chap. 1, it is known that G is an exact potential game with \(\varPhi \) serving as the potential function. Therefore, Theorem 5.1 is proved.    \(\square \)

Theorem 5.1 characterizes the relationship between the interference mitigation game G and the network utility in general network scenarios. For further investigation, the following three scenarios are considered [3]: (i) under-loaded scenario: the number of users is less than that of channels, i.e., \(N<M\), (ii) equally-loaded scenario: the number of users is equal to that of channels, i.e., \(N=M\), and (iii) over-loaded scenario: the number of users is greater than that of channels, i.e., \(N>M\). Then, the properties for the three scenarios are characterized by the following propositions, respectively.

Proposition 2.1

For both under-loaded or equally-loaded scenarios, any pure strategy NE of the interference mitigation game G leads to an interference-free channel selection profile.

Proof

In the two scenarios, all pure strategy NE points correspond to orthogonal channel selection profiles, i.e., a channel is selected by no more than one user. This argument is due to the fact that no user is willing to deviate, as it experiences zero interference. Therefore, any pure strategy NE point is optimal to P1, and makes the network interference-free. Therefore, Proposition 2.1 is proved.    \(\square \)

Proposition 2.2

For the over-loaded scenario, there exists at least one pure strategy NE point that minimizes the expected weighted aggregate interference.

Proof

Multiple pure strategy NE points may exist in the over-loaded scenario but the number of pure strategy NE is hard to obtain. However, according to Theorem 5.1, there is at least one pure strategy NE minimizing the expected weighted aggregate interference. Besides the optimal one, other pure strategy NE points only locally minimize the expected weighted aggregate interference.    \(\square \)

Since the global optimality is not guaranteed in the over-loaded scenarios, it is indispensable to study the performance of NE solutions. Generally, the concept of price of anarchy (PoA) [16] is used to study the performance ratio between the worst NE solution and the social optimum. However, as the PoA for the formulated game is hard to derive, we get an upper bound instead. To begin with, the achievable expected aggregate interference at a pure strategy NE \(a^*=(a^*_1,\ldots ,a^*_N)\) is given by:

$$\begin{aligned} U_{NE}=\sum \limits _{n \in \mathbb {N}} p_n {\mathbf{E }}[I_n]= \sum \limits _{n \in \mathbb {N}} \sum \limits _{m \in \mathbb {\{N} \backslash n\}} p_mp_n \bar{w}^{a^*_n}_{mn}f(a^*_m,a^*_n). \end{aligned}$$
(2.12)

Proposition 2.3

If the values of the expected random components of all channels are the same, i.e., \(\bar{\varepsilon }^s_{mn}=\bar{\varepsilon }^0_{mn}\), \(\forall m,n \in \mathbb {N}\), then the expected aggregate interference of any pure strategy NE solution in an over-loaded scenario is upper bounded by \(U_{NE} \le U_0/M\), where

$$\begin{aligned} U_0=\sum \limits _{n \in \mathbb {N}} \sum \limits _{m \in \mathbb {\{N} \backslash n\}} p_n p_m (d_{mn})^{-\alpha } \bar{\varepsilon }^{0}_{mn} \end{aligned}$$
(2.13)

can be regarded as the expected aggregate interference if all the players choose the same channel.

Proof

Refer to [11].    \(\square \)

Remark 2.2

Generally, \(U_0\) is the worst-case of the expected aggregate interference of an arbitrary network. According to Proposition 2.3, we can see that increasing the number of channels, i.e., M, would decrease the aggregate interference in the network, which can be expected in any wireless networks.

2.4 Achieving NE Using Stochastic Learning Automata

With the interference mitigation problem formulated as a potential game, the next task is to develop distributed learning algorithm to achieve NE. Notably, we encounter with the following incomplete and dynamic information constraints: (i) obtaining information of other players is not feasible, and (ii) the interference channel gains vary randomly from slot to slot. As a result, the commonly used learning algorithms for potential games, e.g., best response dynamic [17], no-regret learning [4], fictitious play [18], and spatial adaptive play [19], cannot be applied. To overcome this problem, we propose a stochastic learning automata [20]-based algorithm, which is simple and completely distributed.

2.4.1 Algorithm Description

To begin with, the game is extended to a mixed strategy form. Specifically, the mixed strategy for player n at iteration k is denoted by the probability distribution \(q_n(k) \in \varDelta ({A}_n)\), where \(\varDelta ({A}_n)\) is the set of all possible probability distributions over the action set \({A}_n\). In the stochastic learning automata algorithm, the game is played only once in a slot. After each play, each player receives a random payoff, which is jointly determined by action profiles of all the users and the instantaneous channel gains. Based on the received payoffs, the players update their mixed strategies using a simple and distributed rule. An illustrative diagram of the stochastic learning automata-based algorithm is shown in Fig. 2.2.

Fig. 2.2
figure 2

The schematic diagram of the stochastic automata learning-based channel selection algorithm

Full size image

Suppose that at the kth slot, the channel selection profile of the users is \(a(k)=\{a_1(k),\dots ,a_N(k)\}\). Then, the random payoff received by player n is as follows:

$$\begin{aligned} r_n(k)=D-\sum \limits _{m \in \mathbb {\{N} \backslash \{n\}\}} p_mp_n(d_{mn})^{-\alpha }\varepsilon ^{a_n(k)}_{mn}f(a_m(k),a_n(k)), \end{aligned}$$
(2.14)

where \(f(\cdot )\) is the indicator function specified by (3.8), and \(\varepsilon ^{a_n(k)}_{mn}\) is the instantaneous channel gain. The purpose of adding the predefined positive constant D to the payoff, is to keep it positive. However, the received payoff may also be negative due to the fluctuation of random channel fading. Thus, the following modified received payoff is used in the distributed learning algorithm:

$$\begin{aligned} r_n(k)=\max \{{r_n(k), 0}\} \end{aligned}$$
(2.15)

The stochastic learning automata-based algorithm is described in Algorithm 1. It is noted that the algorithm is online and fully distributed, as the users adjust the channel selections from their action-payoff history.

figure a

The proposed stochastic learning automata-based algorithm is also called linear reward-inaction (\(L_{R-I}\)), which is a special case of linear learning automata [20]. The updating rules for linear learning automata are generally given by:

$$\begin{aligned} q_n(k+1)=q_n(k)+bF\big (q_n(k),a_n(k),r_n(k)\big ), \end{aligned}$$
(2.18)

where \(F(\cdot ,\cdot ,\cdot )\) is a learning function that maps the current action and payoff to the mixed strategy in the next iteration. Of course, other forms of update rules, e.g., linear reward-penalty and linear reward-\(\varepsilon \)-penalty [20], can also be used. The reason of using \(L_{R-I}\) is that it is simple and can be analyzed when being incorporated with game theory, which will be discussed below. Also, it is noted from (2.18) that it is only relying on the individual trial-payoff history of a player and does not need to know any information of others. In fact, each user is not even aware of other users.

2.4.2 Convergence Analysis

Using the method of stochastic approximation [21], the long-term behavior of the mixed strategies of the users can be characterized by an ordinary differential equation. Specifically, the convergence of the stochastic learning automata algorithm is characterized by the following theorem.

Theorem 2.2

With a sufficiently small step size b, the stochastic learning automata-based learning algorithm asymptotically converges to a pure strategy NE point of an exact potential game.

Proof

Refer to Theorem 5 in [22].    \(\square \)

Based on Theorem 2.2, the aggregate interference performance of the proposed game-theoretic interference mitigation solutions are characterized by the following propositions.

Proposition 2.4

In under-loaded or equally-loaded scenarios, the proposed game-theoretic solution asymptotically converges to an optimal channel selection profile that makes the network interference-free.

Proof

This proposition can be proved by straightforwardly combining Theorem 2.2 and Proposition 2.1.    \(\square \)

Proposition 2.5

In an over-loaded scenario, the proposed game-theoretic solution asymptotically converges a pure strategy channel selection profile and minimizes the expected weighted aggregate interference globally or locally.

Proof

According to Proposition 2.2, there is at least an optimal channel selection minimizing the aggregate interference, and they may be other suboptimal solutions. Thus, Proposition 2.5 is proved.    \(\square \)

Since there are various fading models, e.g., Rayleigh, Nakagami, and log-normal, it is important to study the achievable performance for different fading models. The following proposition reveals an interesting result.

Proposition 2.6

For a given distributed network, the achievable interference performance of the proposed game-theoretic solution is determined by the expected interference gain but not the specific fading model.

Proof

Based on (2.6), it is seen that the expected weighted aggregate interference is jointly determined by user locations, the transmitting power, the final channel selection profile, and the expected interference gain \(\bar{\varepsilon }^s_{mn}\). Thus, for a given distributed network, the achievable performance is only determined by the expected interference gain but the specific fading model.    \(\square \)

According to Proposition 2.6, two fading models with the same expected fading gain, e.g., Rayleigh and Nakagami, would lead to the same expected weighted aggregate interference. Moreover, for a given fading model with unit-mean, the resulting expected weighted aggregate interference would be equal to a nonfading scenario, where only large-scale power-loss is considered.

The above analysis is for time-varying radio environment. As the static environment is an extreme case of time-varying case, we can conclude that stochastic learning automata-based algorithm also converges in static environment.

Proposition 2.7

In a static system with symmetrical interference channels, the proposed game-theoretic solution also asymptotically converges to a pure strategy NE point of the channel selection game.

Proof

The experienced interference of a user in a static system is expressed as:

$$\begin{aligned} \hat{I}_n=\sum \limits _{m \in \mathbb {\{N} \backslash n\}} f(a_m,a_n) p_m \hat{w}^{a_n}_{mn}, \end{aligned}$$
(2.19)

where \(\hat{w}^{a_n}_{mn}\) is the fixed interference gain from users m to n on channel \(a_n\) satisfying \(\hat{w}^{a_n}_{mn}=\hat{w}^{a_n}_{nm}\). Then the aggregate weighted interference in a static network is given by:

$$\begin{aligned} \hat{U}=\sum \limits _{n \in \mathbb {N}} p_n \hat{I}_n= \sum \limits _{n \in \mathbb {N}} \sum \limits _{m \in \mathbb {\{N} \backslash n\}} p_mp_n \hat{w}^{a_n}_{mn}f(a_m,a_n). \end{aligned}$$
(2.20)

Similarly, a static channel selection game \( {{G}}_c\) with the following utility function can be defined:

$$\begin{aligned} \begin{array}{l} \hat{u}_n(a_n,a_{-n})=D-p_n\hat{I}_n. \end{array} \end{aligned}$$
(2.21)

Using similar lines of proof for Theorem 5.1, it can be proved that the channel selection game in static environment is also a potential game with potential function \(-\frac{1}{2}\hat{U}\). Based on this result, we can prove this proposition following the same methodology in Theorem 2.2.    \(\square \)

2.5 Simulation Results and Discussion

The simulation setting is similar to [9], in which the users are randomly located in a \(100\,\mathrm {m}\times 100\) m region. For presentation, the transmitting powers of all the users are set assumed to be \(p_n=0\,\mathrm{{dBw}}, \forall n\in \mathbb {N}\), the path loss exponent is \(\alpha =2\), and the noise power as \(N_0=-130\,\mathrm {dBw}\). For simplicity of analysis, the distance between the transmitter and the receiver for each intracommunication is set to \(1\,\mathrm {m}\), i.e., \(d_{nn}=1, \forall n\in \mathbb {N}\); The channel bandwidth is \(1\,\mathrm {MHz}\). We consider three common fading models: Rayleigh, Nakagami, and log-normal.

2.5.1 Convergence Behavior

2.5.1.1 Convergence Behavior in Dynamic Environment

In this part, we investigate the convergence with time-varying channel gains. Specifically, we consider a network with three channels and five users. Rayleigh fading with unit mean is considered. The positive constant used in the instantaneous received payoff (5.8) and (2.14) is set to \(D=0.005\), and the step size of the learning algorithm is set to \(b=0.1\).

Fig. 2.3
figure 3

The evolution of channel selection probabilities for three arbitrarily selected users in Rayleigh fading environment (\(N=5, M=3, D=0.005\) and \(b=0.1\))

Full size image

The convergence behavior of three arbitrarily selected users is shown in Fig. 2.3. Taking user 1 as an illustrative example, it chooses the channels with equal probabilities at the beginning (\(q_{11}=0.33, q_{12}=0.33, q_{13}=0.33\)), and finally chooses channel 3 (\(q_{11}=1, q_{12}=0, q_{13}=0\)) after 250 iterations. From the figure, the channel selection probabilities of the users converge to pure strategy in about 100, 250, and 290 iterations, respectively. In addition, the evolution of number of the users choosing different channels is shown in Fig. 2.4. It is noted that the number of users selecting different channels keeps unchanged in about 250 iterations, which again validates the convergence of the proposed game-theoretic interference mitigation approach.

Fig. 2.4
figure 4

Evolution of the number of users choosing the channels in Rayleigh fading environment (\(N=5, M=3, D=0.005\) and \(b=0.1\))

Full size image
Fig. 2.5
figure 5

Convergence behavior comparison in static environment ( \(N=20, M=5\), \(D=0.005\) and \(b=0.1\))

Full size image

2.5.1.2 Convergence Behavior in Static Environment

In this part, we study the convergence with static channel gains and compare it with an existing static algorithm. There is an efficient distributed channel selection algorithm, called GADIA, which is proposed by Babadi and Tarokh [9] and has been shown to achieve good performance in static systems. According to Proposition 2.7, the learning algorithm in this chapter also converges in static environment. The convergence comparison results of an arbitrary network topology with 20 users and five channels are shown in Fig. 2.5. It is seen that the proposed learning algorithm also converges, as the GADIA algorithm. However, the GADIA algorithm converges rapidly and smoothly. The reasons are: (i) the GADIA algorithm measures the received interference on all channels before a user updates the channel selection strategy, and the updating procedure is implemented in a deterministic manner, i.e., only one user can update action at a time, whereas (ii) the proposed learning algorithm only measures the received interference on the current chosen channel and the update procedure is implemented in a stochastic manner, i.e., all the users update their actions simultaneously.

2.5.2 Performance Evaluation

2.5.2.1 Performance Comparison for Different Solutions

In this part, the performance of the proposed stochastic automata-based learning algorithm in terms of expected weighted aggregate interference is evaluated. Specifically, we consider a network with five channels, and the number of users increases from 2 to 30. The parameters in the learning algorithm are set as \(D=0.005\) and \(b=0.08\). For comparison, we also consider the following three solutions: the random selection scheme, the worst NE, and the best NE. In the random selection scheme, each user randomly chooses a channel in each slot. Note that the random channel selection seems to be an instinctive method, as the channel gains vary randomly from slot to slot and there is no information exchange. The best (worst) NE are obtained as follows: we run the learning algorithm \(10^3\) times and then choose the best (worst) result, respectively. According to Theorem 5.1, the best NE is global minimum for the expected weighted aggregate interference.

Fig. 2.6
figure 6

Performance evolution for a distributed network involving in Rayleigh fading environment (\(D=0.005\), \(b=0.08\) and \(M=5\))

Full size image

The comparison results of four solutions is shown in Fig. 2.6. By simulating \(10^3\) independent trials, the results are obtained by taking the expected value. Some important conclusions can observed: (i) in the under-loaded and equally-loaded scenarios, i.e., \(N\le 5\), the performance of the stochastic learning solution and is almost the same with the best NE, which follows the fact that the global optimum is asymptotically achieved, as characterized by Proposition 2.4, and (ii) in the over-loaded network scenarios, i.e., \(N>5\), there is a small performance gap between the learning solution and the best NE. The reason is that the stochastic learning algorithm may converge to an optimal or a suboptimal solution, as characterized by Proposition 2.5, and hence it averagely achieves near-optimal performance. In addition, it is seen that even the worst NE results in less aggregate interference than the random selection scheme. Due to incoordination of the random selection scheme, some channels are crowded whereas others are unoccupied. In comparison, the users choose different channels in pure strategy NE solution, which thus results in lower value of interference.

2.5.2.2 Performance Evaluation for Different Fading Parameters

The performance evaluation for different fading parameters is shown in Fig. 2.7. The presenting results are obtained by simulating 20 topologies with \(10^3\) independent trials and then taking the average values. No-fading implies that only large-scale power-loss is considered and 0 dB-mean is with unit-mean. From the figure, it can be observed that the performance gap between No-fading and Rayleigh with 0 dB-mean is trivial. According to Proposition 2.6, their performance should be the same as the expected channel gains are the same. Moreover, as the mean value of Rayleigh fading increases, e.g., increasing from 1 to 3 dB, the caused interference increases as can be expected.

Fig. 2.7
figure 7

The comparison results of expected aggregate interference for different Rayleigh fading parameters (\(D=0.005\), \(b=0.08\) and \(M=5\))

Full size image

2.5.2.3 Performance Evaluation for Different Fading Models

In this part, different fading models are considered. Specifically, the following well-known models including Rayleigh, Nakagami, and Log-normal is considered:

  • In Rayleigh model, the channel gains are exponentially distributed with unit-mean.

  • In Nakagami model, the probability distribution function of the channel gains is determined by \(f(x)=\frac{m^m x^{m-1}}{\varGamma (m)}e^{-mx}, x\ge 0\).

  • In Log-normal model, the channel gains is modeled by a random variable \(e^X\), where X is a Gaussian variable with zero-mean and variance \(\sigma ^2\). Log-normal fading is usually characterized in the dB-spread form which is related to \(\sigma \), by \(\sigma =0.1\log (10)\sigma _\mathrm{{dB}}\). The dB-spread of Log-normal fading typically ranges from 4 to 12 dB as indicated by the empirical measurements [15].

Fig. 2.8
figure 8

The comparison results of expected aggregate interference for different fading models (\(D=0.005\) and \(b=0.08\))

Full size image

The comparison results of expected aggregate interference for different fading models are shown in Fig. 2.8. The results are obtained by simulating 20 independent topologies with \(10^3\) independent trials and then taking the average value. As all the presented fading models are with unit-mean, the interference performance gap is trivial, which directly follows the argument characterized by Proposition 2.6. Also, the comparison results of expected normalized achievable throughput for different fading models are presented in Fig. 2.9. As the number of users increases, the expected normalized achievable rate decreases as expected. Some interesting observations are: (i) Rayleigh fading outperforms Nakagami fading and Log-normal fading, and (ii) the performance of Log-normal fading is almost the same with that of No-fading. We think the reasons may be as follows: (i) multiuser diversity of Rayleigh fading is stronger than those of other fading models, and (ii) the multiuser diversity of Log-normal fading is weak.

Fig. 2.9
figure 9

The comparison results of expected normalized achievable throughput for different fading models (\(D=0.005\) and \(b=0.08\))

Full size image

2.6 Concluding Remarks

Compared with previous studies, the key difference in this chapter is that the channel gains are time-varying. In another work [22], we have studied the opportunistic spectrum access problem with time-varying spectrum opportunities, in which the channel states (idle or occupied) change randomly from slot to slot. The stochastic learning automata algorithm was also used therein and its convergence toward pure strategy NE of potential games was rigorously proved. Note that the most promising property of the stochastic learning automata is that the received payoff can be random or deterministic. As a result, we believe that the methodology used in this chapter provides an efficient approach for solving decision-making problems in time-varying environment, which are common in practical wireless networks.