Algal Reactor Design Based on Comprehensive Modeling of Light and Mixing

Abstract

The prospect of autotrophic (or light-driven) algal biomass production as a sustainable substitute for fossil feedstocks has yet to fulfill its potential. As a likely cause, the inability to robustly account for algal biomass production rates has prevented the derivation of satisfactory mass balances for the simple parameterization of bioreactors. The methodology presented here aims at resolving this shortcoming. Treating photons as a substrate continuously fed to algae provides the grounds to define an autotrophic yield Ф^DW, in grams of dry weight per mole of photons absorbed, as an operating parameter. Under low irradiances, the rate of algal biomass synthesis is the product of the yield Ф^DW and the flux of photons absorbed by the culture, modeled using a scatter-corrected polychromatic Beer-Lambert law. This work addresses the broad misconception that Photosynthesis-Irradiance curves, or the equivalent use of specific growth rate expressions independent of the biomass concentration, can be extended to adequately model biomass production under light-limitation. Since low photon fluxes per cell maximize Ф^DW, the photosynthetic units mechanistic model was adapted to determine a corresponding maximum residence time under high light. Such high speeds in the photic zone, which call for fundamental changes in bioreactor design, enable the use of Ф^DW to describe biomass productivity under otherwise inhibitory irradiances. Nitrogen limitation-induced lipid accumulation corresponds to a photon flux excess with respect to the rate of nitrogen uptake, such that continuous lipid production can be achieved using the Ф^DW and nitrogen quotient parameters. Additionally, energy to photon-counts conversion factors are derived.

1 Introduction

The prospect of autotrophic (or light-driven) algal biomass production as a sustainable substitute for fossil feedstocks holds promise, but has yet to fulfill its potential. Arguably, the discrepancy between theoretical and achieved productivities in the field results from the lack of a working comprehensive algal growth model to guide bioreactor design. Akin to the petroleum industry in the early 50’s, distillation of crude oil heavily relied on trial-and-error and was as a result very wasteful. In the mid-50’s, scientific contributors such as John Prausnitz pioneered molecular thermodynamics to model the behavior of such complex chemicals mixtures (Sanders 2005) . The resulting ability to predict these separation properties has revolutionized the petroleum industry, and is the cornerstone of all petrochemical processes. The approaches introduced by Holland et al. (Holland et al. 2011; Holland and Wheeler 2011) , further detailed in this chapter, hold the potential to provide such model for industrial algal biomass production processes, guiding bioreactor design and parameterization to maximize biomass and lipid productivity.

The inherent particle nature of light as a growth substrate has been broadly overlooked. Treating photons as a substrate continuously fed to algae provides the grounds to define an autotrophic yield , which is key for comparing productivities as well as parameterizing bioreactors. Indeed, within the Photosynthetically Active Radiation (PAR) region, regardless of its energy, an absorbed photon exciting the photosynthetic apparatus drives carbon fixation and therefore biomass synthesis. As such, the concept of biomass yield, reported for heterotrophic growth as biomass produced per mass of input sugar substrate, translates to its autotrophic counterpart by normalizing the biomass produced per number of input photons. The unit of choice for photon counting is the Einstein (E), or mole of photons in the PAR region.

Importantly, the goal of algal bioreactor designs is to maximize yield —not solely productivity. Sun-lit outdoor ponds require land area while artificially lit bioreactors require a primary energy source (wind power or other). Hence light is an expensive substrate that should not be wasted. Biomass productivity is the product of the autotrophic yield per absorbed photon flux. Notably, under conditions of complete absorption of the photons by the algal culture, maximum yield leads to maximum productivity (Sect. 2.1). However, the converse does not hold (Sect. 3.2). Most often, algal productivities are reported (in mass per time per volume or area) with omitted incident light levels or incomplete reactor geometries. This, in turn, precludes yield-based performance comparisons between the various characterized systems. The work presented here introduces routine determination of the algal autotrophic yield as the key parameter for setup evaluation.

Current efforts toward modeling light as a nutrient treat the algal population as a whole system, whose growth rate follows saturation kinetics (Sect. 3.2). For chemical substrates, the Monod saturation kinetics reflect that the microbial population growth rate increases with increasing concentration, and saturates when the substrate reaches a concentration greater than its uptake affinity. In chemostat bioreactors , such microbial populations reach highest productivities at high substrate concentrations supporting near maximum growth rates. For light as a substrate, Photosynthesis-Irradiance (PI) curves describe the saturation behavior of the algal population growth rate (or specific rate of biomass increase) as a function of incident light. In a given bioreactor, while productivity increases with incident light levels until light excess is reached, the biomass yield decreases. As proof, at a given biomass concentration with known cell geometry, PI curve data can be used to calculate the biomass yield (from the ratio of specific growth rate to irradiance), which shows a maximum at low irradiance. As further evidence, fluorescence response studies show highest quantum yields at low light levels (Sect. 3.1). In the authors’ opinion, an apparent analogy between PI curves and Monod saturation kinetics has laid the ground for widespread misleading analyses for biomass productivity calculations as well as optimization.

Once established that highest yields are reached at low light intensity , inhibitory light levels reached at the surface of most outdoor systems can be treated using two distinct methodologies. The more widespread approach is to model cell damage and energy losses as unavoidable consequences of growth. As a contrast, the work presented here uses the same mechanistic model to derive bioreactor characteristics enabling highest yields under high irradiance. Indeed, in a dense algal culture, high speeds across the photic zone allows for high frequency light-dark fluctuations, which therefore reduce photon flux per cell to levels conducive to high yield biomass production. Through deriving target bioreactor properties from strain attributes, this new paradigm provides a reliable framework to estimate outdoor productivities from yields determined experimentally under low light.

Provided adequate agitation to sustain high yield biomass production, steady-state biomass production can be easily parameterized using the autotrophic yield . Achieving such a steady-state is key to maximizing productivity . The set of simple equations presented in this work, the validity of which hinges on vigorous mixing conditions under high irradiance, averts the complex control strategies detailed in the literature.

Algal lipid accumulation has been broadly documented under nitrogen limitation in growth arrested cultures. However, growth arrest lowers overall lipid productivity and can lead to erroneous productivity projections (Wilhelm and Jakob 2011; Rodolfi et al. 2009) . The concept of light as a continuously fed substrate brings about a different understanding of such lipid accumulation. Namely, lipid accumulation corresponds to a photon flux excess with respect to the flux of nitrogen molecules taken up by the culture , which can be parameterized under steady-state (Sect. 5.3). Upon determination of the culture autotrophic and nitrogen yields under nutrient-replete conditions, the nitrogen flux is lowered gradually until lipid production is achieved—at the cost of a lowered overall dry-weight productivity. This chapter details the methodology to achieve continuous autotrophic lipid production.

2 Sustainable Algal Lipid Production: Current Achievements and Upcoming Prospects

2.1 Biomass and Lipid Production Estimates

Algal lipids have been widely promulgated as a precursor to renewable transportation biofuels. Stress-induced autotrophic lipid accumulation has been documented in many algal species (Rodolfi et al. 2009; Griffiths and Harrison 2009) , including phosphate limitation in Ankistrodesmus falcatus (Kilham et al. 1997) , silicon and nitrogen deficiency (Tornabene 1983; Sheehan et al. 1998; Shifrin and Chisholm 1981) and alkaline pH stress in Chlorella sp. (Guckert and Cooksey 1990) . However, lipid accumulation under these stress conditions—on the order of 20–40 % on a dry weight (DW) basis—have invariably been associated with prolonged growth arrest or severe growth rate reduction (Reitan et al. 1994; Gressel 2008) .

Reported outdoor algal biomass productivities are on the order of 20–40 g_DW m⁻² d⁻¹ (Capo et al. 1999; Lundquist et al. 2010) under nutrient-replete conditions for average yearly irradiances of 390 µE m⁻² s⁻¹ (such as in southern US latitudes). As an oft-neglected consequence, the corresponding upper bound of lipid productivity (16 g_LIPIDS m⁻² d⁻¹ or 7,400 gal acre⁻¹yr⁻¹ at a lipid density of 850 g L⁻¹ and 40 % lipids) needs to be lowered to account for the duration of the culture maturation and growth arrest. Indeed, the sole requirement of a one-day nitrogen starvation period to achieve high lipid content in a culture growing at 40 g_DW m⁻² d⁻¹ would half the above lipid productivity upper bound estimate to 8 g_LIPIDS m⁻² d⁻¹.

Upon nitrogen limitation and subsequent lipid accumulation, the cell specific energy increases due to the higher specific energy of lipids, which is illustrated in Table 1 with representative values of algal cell compositions. Assuming a constant photosynthetic efficiency despite mild stress, nitrogen-limited lipid productivity estimates from nitrogen-replete productivity data should reflect the difference in DW specific energy, and should therefore be multiplied by 0.79 for the example given in Table 1.

Table 1 Example increase in dry weight specific energy in nitrogen-limited algal cells

Measured quantum efficiencies of 0.102 g_C/mole photons in algae (Cleveland et al. 1989) correspond to an achievable productivity of 82 g_DW m⁻² d⁻¹, assuming 50 % C on a dry weight basis (Kroon and Thoms 2006) and average yearly irradiances of 390 µE m⁻² s⁻¹. Such two- to four- fold increase in large-scale algal biomass productivity may be achievable using the methodology and insights provided in this work. Furthermore, understanding algal metabolism in a way to achieve continuous lipid production at high biomass productivities would permit lipid productions on the order of 16 g_LIPIDS m⁻² d⁻¹ (25 % harvestable lipids from cells containing 30 % on a DW basis, at 390 µE m⁻² s⁻¹, and corrected for higher specific energy content of lipid-rich cells as in Table 1) or 7,500 gal acre⁻¹yr⁻¹ (at a lipid density of 850 g L⁻¹). For comparison with crop-based agriculture, Malaysia palm oil productivity was 473 gal acre⁻¹ yr⁻¹ in 2008 (Malaysian Palm Oil Industry Performance 2008 (Anon 2009), with a density of 890 g L⁻¹), which is 16-fold less than the projected algal lipid productivity.

2.2 Irradiance Unit Conversions

Energy calculations of achievable productivity depend on the measurement of incident light as a Photosynthesis Photon Flux Density (PPFD, in µE m⁻² s⁻¹) in the PAR region between 400 nm and 700 nm. While quantum meters readily provide such measurements, outdoor light levels are commonly reported in W m⁻² using a pyranometer . Unit conversions between photon flux and energy are derived using corresponding light source spectra.

Two geometries of sensors are commonly used in the field to measure incident light, either as energy per area or photon flux per area. The more common 2π half-sphere sensors measure light incident onto a surface, and the 4π full-sphere sensors measure light incident from all directions. The use of 4π sensors, which can give readings up to twice those of 2π sensors, is more relevant for bioreactors at an angle from the ground, whereas 2π sensors are more relevant for pond configurations. For complex reactor geometries, (Sánchez Mirón et al. 2000) used chemical actinometry to measure the precise incident PPFD . In our analysis below, we assume the use of 2π sensors to quantify direct normal-incident PPFD.

Solar radiation spectra are typically reported as a plot of photon energy E _P(λ) (in W m⁻² nm⁻¹) measured for each wavelength increment dλ (ASTM 2003; Thuillier et al. 2003) . The photon energy E _P(λ) is proportional to the photon flux $\dot n( \lambda)$:

$$ {E_P}( \lambda)d\lambda= \dot n( \lambda) \cdot Na \cdot \frac{{hc}}{\lambda }d\lambda$$

(1)

where h is Planck’s constant in S.I. units; c the celerity of light in m s⁻¹; Na is Avogadro’s constant in mol⁻¹; E _P(λ) is the energy reported for each wavelength increment dλ at λ in W m⁻² nm⁻¹; $\dot n( \lambda)$ is the photon flux reported for each wavelength increment dλ at λ in Einstein s⁻¹ m⁻² nm⁻¹. These solar spectra can thus be used to convert units of Einstein and Joules (c _EJ in units of E J⁻¹), with Einstein as the photon flux in the PAR region, and total energy measured in the wavelength range λ₁- λ₂:

$$ {c_{EJ}} = \frac{{\int\limits_{400}^{700} {\dot n} ( \lambda)d\lambda }}{{\int\limits_{\lambda 1}^{\lambda 2} {{E_P}} ( \lambda)d\lambda }} = \frac{{{{10}^{ - 9}}}}{{h \cdot c \cdot Na}}\frac{{\int\limits_{400}^{700} {\lambda\cdot {E_P}} ( \lambda)d\lambda }}{{\int\limits_{\lambda 1}^{\lambda 2} {{E_P}} ( \lambda)d\lambda }} $$

(2)

Analogously, spectra measured in W m⁻² nm⁻¹ can be converted to a normalized photon flux frequency PSUN(λ) in nm⁻¹ in the PAR region (Fig. 1):

Fig. 1

Normalized photon frequency in the PAR region for the acquired fluorescent light spectrum and calculated for the ASTM ground direct-normal spectrum (Eq. 3)

$$ {P_{SUN}}( \lambda) = \frac{{\lambda\cdot {E_P}( \lambda)}}{{\int\limits_{400}^{700} {\lambda\cdot {E_P}( \lambda)d} \lambda }} $$

(3)

The fraction of energy in the PAR region, given a total energy measured in the wavelength range λ₁–λ₂, is:

$$ {F_{PAR}} = \frac{{\int\limits_{400}^{700} {{E_P}} ( \lambda)d\lambda }}{{\int\limits_{\lambda 1}^{\lambda 2} {{E_P}} ( \lambda)d\lambda }} $$

(4)

Percent energy in the PAR region as well as Einstein-to-Joules conversion factors are reported in Table 2. Outer space (Space) spectrum data was kindly provided by Dr. Thuillier (Thuillier et al. 2003) . For ground irradiance, ASTM spectra (ASTM 2003) were used as reference ground spectra, for a 37˚ tilted surface (Tilted) and a direct-normal surface (Flat). The ASTM spectra are reported for an air-mass (AM) coefficient of 1.5, which provides a description on the relative light attenuation due to atmospheric water vapor concentration (Mecherikunnel et al. 1983) , at conditions still conducive to photovoltaic applications (ASTM 2003). The wavelength ranges were chosen to reflect apparatus available commercially, such as a Li-Cor pyranometer , usually 400–1100 nm range, (Kania and Giacomelli 2001) or a Precision Spectral Pyranometer (PSP, 285–2800 nm range), used by the NREL (http://rredc.nrel.gov/solar/pubs/redbook/) for its solar radiation measurements.

Table 2 Einstein-to-Joules conversion factors c _EJ and Percent energy in the PAR region. An outer space spectrum (Space), an ASTM 37˚ tilted ground spectrum (Tilted) and an ASTM ground direct-normal spectrum (Flat) were used

Despite marked variations in the overall sun spectrum due to an air-mass coefficient AM of 1.5, the conversion factors and percent energy calculations do not vary significantly between ground and outer-space data (Table 2). This is likely due to the fact that the ground solar spectrum in the PAR region changes drastically in shape for AM > 1.5 but not below (Mecherikunnel et al. 1983) . These tabulated values provide an updated tool which should help prevent the use of erroneous conversion factors (Kania and Giacomelli 2001) .

As photosynthesis is known to occur in the near-UV range between 350 and 400 nm (Sakshaug and Johnsen 2006) , the various reference spectra were used to calculate the % photon flux in the near-UV range compared to the flux in the 350–700 nm range (near UV + PAR). These values were 5.76 % (Space), 3.94 % (Flat) and 4.89 % (Tilted), such that the near-UV contribution can be mostly neglected for outdoor level estimates.

Spectrometers allow for the acquisition of light source spectra in the PAR region, where the count reading P(λ) in a given increment dλ is proportional to the photon flux $\dot n( \lambda)$ by a constant β:

$$ P( \lambda) = \beta\cdot \dot n( \lambda) = \frac{\beta }{{h \cdot c \cdot Na}} \cdot \frac{{{E_P}( \lambda)}}{\lambda } $$

(5)

These relative photon-count spectra can therefore be used to calculate c _EJ (in units of E J⁻¹) the conversion from Einstein to Joules (or E s⁻¹ to W), as shown above, where both PPFD and energy are measured in the PAR region:

$$ {c_{EJ}} = \frac{{{{10}^{ - 9}}}}{{h \cdot c \cdot Na}}\frac{{\int\limits_{400}^{700} P ( \lambda)d\lambda }}{{\int\limits_{400}^{700} {\frac{{P( \lambda)}}{\lambda }} d\lambda }} $$

(6)

Two P(λ) spectra for fluorescent light sources of different intensities were acquired using an Ocean Optics spectrometer (in the 400–700 nm range), in both cases resulting in calculated conversion factor c _EJ  = 4.49 µE J⁻¹. An incident PPFD of 50 µE m⁻² s⁻¹, for example, provides a culture with an energy of 11.1 W m⁻².

2.3 Sustainability Considerations

Achieving sustainable biomass production from algae entails a comprehensive analysis of the overall process, for which all feedstocks and energy sources should be renewable . Hence, providing flue gas from coal fired plants as a CO₂ source (Vunjak-Novakovic et al. 2005) , chemical fertilizers as nutrient sources , or nuclear energy to power algal bioreactors represent examples of unsustainable processes. Since sugar feedstocks are currently plant-derived and therefore require fossil-based pesticides, fertilizers and processing, algal lipid production under heterotrophic conditions (Xu et al. 2006; Liang et al. 2009) does not constitute a long term transportation fuel energy solution.

Large-scale production relies on the supply of tremendous volumes of freshwater. Indeed, while the prospect of using seawater algae seems attractive, algal biomass processing requires mechanical steps sensitive to corrosion by seawater. In addition, evaporation leads to an inhibitory increase in the bioreactor salinity unless fresh make-up water is added or unless the operation is periodically shut down and restarted. Efficient water recycling provides a partial solution to the environmental impact associated with such water management . Unlike plants, algae do not rely on evaporative cellular processes to avert overheating under high light, such that the net area water consumption of algae is comparatively lower than crops provided water recycling (Table 1 in Yang et al. (2010) and Table 2 in Gerbens-Leenes et al. (2009)) . Processing algal biomass at a concentration of 2 g_DW/L and 25 % harvestable lipids (density of 850 g L⁻¹) contributes 1700 L_WATER/L_LIPIDS ⁻¹, but only 85 L_WATER/L_LIPIDS ⁻¹ with 95 % recycling. Evaporation rates estimated from US “pan” evaporation data (Farnsworth and Thompson 1982) are on the order of 55–120 cm d⁻¹, which represent 285–520 L_WATER/L_LIPIDS ⁻¹ for an algal lipid production of 16 g_LIPIDS m⁻² d⁻¹. These values are much lower than rapeseed (14,200 L_WATER/L_LIPIDS ⁻¹) or Jatropha (19,900 L_WATER/L_LIPIDS ⁻¹) (Gerbens-Leenes et al. 2009) . Nevertheless, rainwater collection, desalination and/or wastewater supply are key to reduce adverse environmental effects associated with freshwater consumption.

The sustainable supply of nutrients can be achieved through integration of Anaerobic Digesters (AD) in various configurations. AD microbial populations metabolize residual high energy carbon from the fed biomass into biogas , which is a mixture of about 55 % methane and 45 % CO₂, and a concentrated NP-rich effluent (Lansche and Müller 2009; Möller and Müller 2012; Nasir et al. 2012) . Oswald and co-workers realized visionary designs integrating AD and algal biomass production as early as the 50’s (Oswald and Golueke 1960; Golueke et al. 1957; Golueke and Oswald 1959; Bailey Green et al. 1996) . In the open-loop configuration (Fig. 2), light energy is used to convert organic waste streams (such as manure) into lipids, clean water and a residual biomass rich in protein and carbohydrates. The high oxygen content of the algal pond reduces the pathogen count of the waste stream (Mata-Alvarez et al. 2000) , such that the residual biomass can be used directly as fertilizer (Mulbry et al. 2005) , animal feed (Wilkie and Mulbry 2002) , or further processed into sugars. Once primed with nutrients , the closed configuration (Fig. 3) results in the net conversion of light energy and water into lipids. Valorization of the biogas into energy produces a CO₂ stream which is combined with the air stream and bubbled into the algae photobioreactor. Achieving sustained water and nutrients recycling necessitates the use of biodegradable flocculating agents such as bacterial cultures (Kurane et al. 1986; Oh et al. 2001) , cationic starches (Pal et al. 2005) or biopolymers such as chitosan (Divakaran and Sivasankara Pillai 2002) .

3 Autotrophic Biomass Yield Ф^DW and Scatter-corrected Extinction Coefficient σ^DW

3.1 Algal Biomass Yield Ф^DW

Autotrophic batch algal cultures receive a continuous supply of photons as their source of energy. At low light regimes, most absorbed photons (> 80 %) are used for photochemical reactions (Baker 2008) , which is reflected by an elevated quantum efficiency (in mole CO₂ absorbed per Einstein). Assuming a nutrient-replete environment and low light, algal autotrophic growth in a batch reactor (such as a flask) is analogous to heterotrophic bacterial growth in fed-batch , for which energy is provided by a continuously fed organic carbon substrate (such as glucose). For heterotrophs, vigorous mixing ensures that the fed substrate is homogeneously distributed and taken-up within the culture, which enables the determination of a yield (g_DW g_SUBSTRATE ⁻¹) to predict the culture growth behavior (Blanch and Clark 1997; Yamanè and Shimizu 1984) . In a dense illuminated culture, the photon flux per cell is inherently inhomogeneous, due to the exponential decrease of flux as a function of depth (Yun and Park 2003) . However, under conditions of low photon flux per cell, the rate of biomass production occurs at its maximum quantum efficiency everywhere in the culture, such that, on average (spatial and temporal), the rate of biomass production is proportional to the rate of light absorption by the algal culture. As discussed in Sect. 4, low photon flux per cell can be achieved under low irradiance, or under elevated light with vigorous mixing.

The fed-batch analogy guides the establishment of the algal growth behavior descriptive equations and the existence of an intrinsic autotrophic yield Ф^DW , expressed in g_DW µE⁻¹.

Nutrient-replete algal growth under excess low light follows an exponential behavior in batch cultures, independent of the light input and is described by:

$$ \frac{{d( {{V_C} \cdot C} )}}{{dt}} = \mu\cdot {V_C} \cdot C $$

(7)

where t is the duration (in h) in the light phase; C is the algal culture biomass concentration (in g_DW m⁻³) at time t; V _C is the batch culture constant volume (in m³); µ is the algal culture specific growth rate (in h⁻¹). In the dark phase, the supply of energy to the algal culture is effectively interrupted. Hence, the time t, as used in this work, represents the cultivation time in the light phase, which is the total growth duration reduced by the duration in the dark.

As the algal culture density increases, the light input becomes limiting. The culture biomass production rate transitions to a non-exponential behavior, and the following equation describes the system behavior, as based on derivations for fed-batch heterotrophic cultures (Yamanè and Shimizu 1984) :

$$ \frac{{d( {{V_C} \cdot C} )}}{{dt}} = {\Phi ^{DW}}[ {{I_0} \cdot {A_C} - {I_{OUT}} \cdot {A_C} - {m_P} \cdot {V_C} \cdot C} ] $$

(8)

where I ₀ is the incident Photosynthesis Photon Flux Density (PPFD, in µE m⁻² h⁻¹); A _C is the area of the culture perpendicular to the light source (in m²); I _OUT is the transmitted/scattered PPFD (in µEm⁻² h⁻¹); Φ^DW is the autotrophic yield (in g_DW µE_absorbed ⁻¹); m _P is the maintenance energy to sustain biomass (in µE g_DW ⁻¹ h⁻¹). I ₀ can be routinely measured at the algal culture-incident light interface using a quantum meter .

Measurements of cellular parameters have shown that housekeeping metabolism in the dark is minimal (G. Finazzi, personal communication and Finazzi and Rappaport (1998)) . In addition, biomass loss was consistently not observed during the dark phase (Holland et al. 2011) . Thus, the algal biomass maintenance parameter is considered negligible, setting: m _P = 0.

As a consequence, at all times of growth, the rate of biomass production is proportional to the amount of light absorbed by the culture:

$$ \frac{{d( {{V_C} \cdot C} )}}{{dt}} = {\Phi ^{DW}}{A_C}{I_{ABS}} $$

(9)

in which I _ABS, the absorbed PPFD (in µE m⁻² h⁻¹) is:

$$ {I_{ABS}} = {I_0} - {I_{OUT}} $$

(10)

I _ABS is the absorbed PPFD (in µE m⁻² h⁻¹)

Assuming the light becomes limiting, the fraction of the incident light which is not absorbed by the algae becomes negligible and the known incident PPFD I ₀ is fully absorbed by the culture, such that:

$$ {I_0} = {I_{ABS}} $$

(11)

Therefore, under light limitation, growth becomes linear:

$$ \frac{{d( {{V_c} \cdot C} )}}{{dt}} = {\Phi ^{DW}} \cdot {I_0} \cdot {A_C} $$

(12)

In the heterotrophic case, the biomass yield can be used in the linear growth region (limiting substrate) to infer volumetric productivity of biomass, if given the culture maintenance parameter m _P, the substrate feeding rate, and the bioreactor volume (Yamanè and Shimizu 1984) .

Since unabsorbed photons cannot accumulate within the batch culture volume, at the onset of light-limitation, both Eqs. 7 and 12 hold true, thereby defining an exponential-to-linear transition (ELT) . The ELT occurs at the point of maximum biomass productivity along the exponential phase, after which a constant productivity is reached in the linear phase. At the ELT, Eqs. 7 and 12 simplify to, at constant volume V _C:

$$ {\left. {\frac{{dC}}{{dt}}} \right|_{transition}} = {\Phi ^{DW}} \cdot {I_0} \cdot \frac{{{A_C}}}{{{V_c}}} = \mu\cdot C\left| {_{transition}} \right. $$

(13)

These equations allow for the determination of Ф^DW as Ф^{DW, ELT} from the region of maximum productivity during batch growth, either as the maximum productivity in the exponential phase or the constant productivity during the linear phase, as detailed in Holland et al. 2011) . As an example, the transition from exponential to linear growth under nutrient-replete conditions has been documented in Van Wagenen et al. (2012) and in Huesemann et al. (2013) .

Under conditions of low PPFD per cell, full incident light absorption and a planar geometry, the experimentally determined autotrophic yield Ф^DW allows for the estimate of a maximum area productivity P ^MAX (in g_DW m⁻² d⁻¹) as:

$$ {P^{MAX}}( {{I_0}} ) = {\Phi ^{DW}} \cdot {I_0} $$

(14)

I ₀ is the average incident PPFD (in µE m⁻² d⁻¹) at the site of interest.

3.2 Scatter-corrected Polychromatic Beer-Lambert Law

In order to model the flux of light absorbed by algal suspensions, measurements of absorbance using a spectrophotometer or photon fluxes using a quantum meter are routinely performed at varying culture depth and concentration, and the data is subsequently fitted (Yun and Park 2001, 2003; Barbosa et al. 2003a, b; Ragonese and Williams 1968) . These planar geometry detection apparatus count scattered photons as effectively absorbed by the algal suspension. However, elastic scattering on whole algal cells does not incur energy loss, such that the scattered photons can be used by the algal culture for photosynthesis (Welschmeyer and Lorenzen 1981) . In other words, a scattered photon which does not reach the detector at a depth x from the light incidence surface can still be used by algal cells at a depth x-dx. Therefore, models to estimate photon fluxes as a function of culture depth or concentration should be based on scatter-corrected absorbance or PPFD data.

Scatter-corrected absorbance data was first acquired using an integrating sphere (Welschmeyer and Lorenzen 1981) . Alternatively, pigment discoloration may be performed by using sodium hypochlorite (NaClO) as described by Ferrari and Tassan (1999) . Since after pigments discoloration, the algal culture absorbance Abs _SCATTER (λ) solely reflects scatter, the scatter-corrected (SC) absorbance spectrum Abs _SC (λ) is obtained from the raw absorbance spectrum Abs _RAW (λ) as shown in Fig. 4:

Fig. 2

Open-loop configuration (wastewater to biofuel, clean water and fertilizer)

Fig. 3

Closed-loop configuration (atmospheric CO₂ and water to lipids and methane)

Fig. 4

Example absorbance spectra for Chlorella vulgaris in nutrient-replete medium

$$ Ab{s_{SC}}( \lambda) = Ab{s_{RAW}}( \lambda) - Ab{s_{SCATTER}}( \lambda) $$

(15)

Below, the Beer-Lambert model is adapted to account for the polychromatic nature of the light source. The wavelength λ spans the Photosynthetically Active Radiation (PAR) region, between 400 and 700 nm. At each wavelength λ, the light absorbed between the depth z and z + Δz is proportional to the incident light flux at depth z, the concentration of algae cells C, the absorption cross-section σ, and the liquid depth Δz through which the light travels:

$$ I( {z + \Delta z,\,\lambda } ) - I( {z,\,\lambda } ) =- C \cdot \sigma ( \lambda) \cdot I( {z,\,\lambda } ) \cdot \Delta z $$

(16)

z is the distance (in m) from the surface of light incidence; λ is the light wavelength (in nm); I(z, λ) is the photon flux density (in µE m⁻² s⁻¹) at depth z and wavelength λ; C is the algal culture biomass concentration (in g_DW m⁻³); σ(λ) is the algal culture absorption cross section (in m² g_DW ⁻¹) at a given λ; Δz depth (in m) over which the photon-flux balance is performed.

Performing the summation of Eq. 16 over the PAR spectrum wavelengths:

$$ \sum\limits_{\lambda= 400}^{700} {I( {z + \Delta z,\,\lambda } )}- I( {z,\,\lambda } ) =- C \cdot \Delta z \cdot \sum\limits_{\lambda= 400}^{700} {I( {z,\,\lambda } )}\cdot \sigma ( \lambda) $$

(17)

The photon flux at depth z at each wavelength can be decomposed as follows:

$$ I( {z,\,\lambda } ) = {P_{LIGHT}}( \lambda) \cdot I( z ) $$

(18)

where P _LIGHT is the wavelength-dependent photon fraction (in nm^-1 ) of the light source, determined from the light source emission spectrum E _LIGHT(λ) acquired using a spectrometer:

$$ {P_{LIGHT}}( \lambda) = \frac{{{E_{LIGHT}}( \lambda)}}{{\int\limits_{400}^{700} {{E_{LIGHT}}( \lambda)} d\lambda }} $$

(19)

Combining Eqs. 17 and 18, and taking the limit $\Delta z \to 0$:

$$ \sum\limits_{\lambda= 400}^{700} {{P_{LIGHT}}} ( \lambda) \cdot \frac{{\partial I( z )}}{{\partial z}}dz =- C \cdot dz \cdot \sum\limits_{\lambda= 400}^{700} {{P_{LIGHT}}} ( \lambda) \cdot I( z ) \cdot \sigma ( \lambda) $$

(20)

From the definition of P _LIGHT (Eq. 19), the following relation holds:

$$ \sum\limits_\lambda ^{spectrum} {{P_{LIGHT}}( \lambda) = 1}$$

(21)

Equation 20 becomes:

$$ \frac{{dI( z )}}{{I( z )}} =- C \cdot dz \cdot \sum\limits_{\lambda= 400}^{700} {{P_{LIGHT}}} ( \lambda) \cdot \sigma ( \lambda) $$

(22)

Integration of the Eq. 22 between depths z = 0 and z = L yields:

$$- \ln \left( {\frac{{{I_L}}}{{{I_0}}}} \right) = C \cdot L \cdot \sum\limits_{\lambda= 400}^{700} {{P_{LIGHT}}} ( \lambda) \cdot \sigma ( \lambda) $$

(23)

where I ₀ is the incident photon flux density (in µE m⁻² s⁻¹) at depth z = 0; I _L is the incident photon flux density (in µE m⁻² s⁻¹) at depth z = L; L is the culture depth (in m) over which the photon flux balance is performed.

The scatter-corrected absorption spectrum $Abs_{SC}^E(\lambda )$ is determined in a cuvette of thickness L _E (in m) at an arbitrary cell concentration C _E (in g_DW m⁻³). At a single wavelength λ, the Beer-Lambert law states that:

$$ \sigma ( \lambda) = \frac{{\ln 10 \cdot Abs_{SC}^E( \lambda)}}{{{C_E} \cdot {L_E}}} $$

(24)

Combining Eqs. 23 and 24:

$$- \ln \left( {\frac{{{I_L}}}{{{I_0}}}} \right) = C \cdot L \cdot \sum\limits_{\lambda= 400}^{700} {{P_{LIGHT}}} ( \lambda) \cdot \frac{{\ln 10 \cdot Abs_{SC}^E( \lambda)}}{{{C_E} \cdot {L_E}}} $$

(25)

Hence the absorbed PPFD I _ABS (in µE m⁻² s⁻¹) by a culture of concentration C and depth L is

$$ {I_{ABS}}( {C,L} ) = {I_0} - {I_L} = {I_0}[ {1 - \exp ( { - {\sigma ^{DW}}CL} )} ] $$

(26)

where the scatter-corrected light source-dependent extinction coefficient σ^DW (in m² g_DW ⁻¹) is:

$${{\sigma }^{DW}}=\frac{\ln 10}{{{C}_{E}}\cdot {{L}_{E}}}\cdot \int\limits_{400}^{700}{{{P}_{LIGHT}}\left( \lambda \right)\cdot Abs_{SC}^{E}\left( \lambda \right)\cdot d\lambda }$$

(27)

Yun and Park found that the hyperbolic model fitted raw absorbance measurements as a function of concentration better than the Beer-Lambert law or the Cornet model (Yun and Park 2001) . After scatter correction, as shown in Fig. 5, this observation still holds true. However, the Beer-Lambert approximation offers a mathematical simplicity which allows for full parameterization of the PPFD from a single scatter-corrected absorbance spectrum (Eqs. 26–27). As a contrast, using the hyperbolic model would require fitting Abs _SC(λ,C) at each wavelength increment using two parameters ω(λ) in m² g_DW ⁻¹ and ψ(λ) in m² g_DW m⁻²:

Fig. 5

Chlorella vulgaris culture UTEX 2714 monochromatic scatter-corrected absorbance as a function of concentration in g L⁻¹. Absorbance measurements at 450 nm (blue) and 550 nm (red). Hyperbolic fit (solid lines) and Beer-Lambert linear fit (dashed lines)

$$ Abs_{SC}( {\lambda ,\,{C_E}} ) = \frac{1}{{\ln 10}}\frac{{\omega ( \lambda){C}{E}}}{{\psi ( \lambda) + {C}{E}}} $$

(28)

The corresponding hyperbolic parameters can subsequently be used to estimate the absorbed PPFD $I_{ABS}^{HYPER}$ (in µE m⁻² s⁻¹) by a culture of concentration C and depth L as:

$${{I}_{ABS}}\left( C,L \right)={{I}_{0}}-{{I}_{L}}={{I}_{0}}\left[ 1-\exp \left(-{{\sigma }^{DW}}CL \right) \right]$$

(29)

Thus, the Beer-Lambert approximation affords a much needed simplicity for the determination of the autotrophic yield , as described in Sect. 2.3.

3.3 The Ragonese and Williams Model

As shown above and as stated by Ragonese and Williams (1968) , algal biomass production is proportional to the amount of light absorbed by the culture. Therefore, using the Beer-Lambert model and combining Eqs. 9 and 26 to account for scatter correction:

$$ \frac{dC}{dt}=\frac{{{\Phi }^{DW}}\cdot {{I}_{0}}}{L}\left[1-\exp \left( -{{\sigma }^{DW}}\cdot L\cdot C \right) \right] $$

(30)

This differential equation can be solved explicitly to allow for the determination of the autotrophic yield Ф^DW from batch growth data C(t):

$$\frac{L}{{{I}_{0}}}\cdot \left\{ C-{{C}_{0}}+\frac{1}{{{\sigma }^{DW}}\cdot L}\cdot \ln \left[ \frac{1-\exp \left[ -{{\sigma }^{DW}}\cdot L\cdot C\left( t \right) \right]}{1-\exp \left[-{{\sigma }^{DW}}\cdot L\cdot {{C}_{0}} \right]} \right]\right\}={{\Phi }^{DW}}\cdot t $$

(31)

where the variables are defined above. A linear least-squares fit forced to the origin of the Eq. 31 left hand side (LHS) vs. time t allows for determination of the autotrophic yield Ф^DW , as shown in Fig. 6. As for bacterial cultures, monitoring the algal biomass concentration is easily done by correlating dry weight and optical density at 680 nm (or other wavelength in the 500–700 nm range) using a spectrophotometer without correcting for scatter (Holland et al. 2011) .

Fig. 6

LHS of Eq. 31 (in g_DW E⁻¹ h⁻¹) as a function of time in h for algal cultures grown in sealed nutrient-replete medium with carbonate added. Cultures of environmental sample (red), Monoraphidium sp. (blue) and Dunaliella primolecta (green) grown with 3 mM nitrate as described in Holland et al. (2011). Linear fit forced to the origin (solid lines)

4 Photosynthetic Efficiency Is Highest At Lower Irradiances

4.1 Fluorescence Response

In an algal culture, the absorbed photons are either processed into biomass through the generation of an electron flow or dissipated (as chlorophyll fluorescence or heat). Photosynthetic electron transport can be modeled as a two-phase process. First, the photosystem II (PSII) is excited by light which results in reduction of the first quinone PSII electron acceptor, Q_A. PSII centers with oxidized Q_A are referred to as ‘open’ while those with reduced Q_A as ‘closed’ (Baker 2008) . The PSII operating efficiency Ф^PSII, which is the product of the fraction of open PSII centers and the quantum yield of photochemistry in these open PSII centers, is a measure of the photon fraction channeled into Q_A reduction. Second, the high energy electron from Q_A is transferred to a series of carriers down an electrochemical gradient, which generates ATP and reducing equivalents for biosynthesis. An increase in the fraction of closed PSII leads to a decrease in Ф^PSII and a concurrent increase in non-photochemical quenching (NPQ) , which dissipates the absorbed photons as heat.

Algal physiologists routinely quantify quantum yields as Ф^CO2 (or Ф^O2) in mole CO₂ fixed (or mole O₂ evolved) per mole photons absorbed, for which gas exchange probes are used to monitor O₂ or CO₂ levels. The saturation pulse method analysis of chlorophyll fluorescence (or chlorophyll fluorescence quenching analysis) has been developed as a noninvasive tool to monitor photosynthetic performance in algae and plants (Baker 2008; Schreiber 2004; Schreiber et al. 1986) . This technique allows for the measurement of the operating efficiency Ф^PSII, which provides an estimate of the linear electron flux through PSII, as well as the fraction of open PSII centers q _L. Over a range of light intensities and CO₂ concentrations, good correlations between Ф^PSII and quantum yields Ф^CO2 have been shown (Baker 2008; Holmes et al. 1989; Campbell et al. 1998; Oberhuber and Edwards 1993; Genty et al. 1989) . As can be seen in Fig. 7, Ф^PSII decreases with increasing irradiance, which is indicative of a reduction in quantum yield Ф^CO2. Indeed, at high photon flux per cell, the decreased fraction of open PSII centers, measured as q _L, leads to an increase in NPQ . Hence, fluorescence response data provide evidence that the autotrophic yield is highest at lower photon flux per cell.

Fig. 7

Representative trends of PSII operating efficiency Ф^PSII (solid lines) and fraction of open PSII centers q _L (dashed lines) as a function of irradiance under high CO₂ (red lines) and low CO₂ (blue lines). Data trend reproduced from Kramer et al. (2004)

4.2 PI Curves

Photosynthesis-irradiance (PI) curves are obtained by subjecting an algal culture, at a given biomass density, to various levels of incident light and measuring O₂ evolution (Grobbelaar 2006; Macedo et al. 1998) . Since the rate of O₂ evolved reflects the rate of biomass production, rates of photosynthesis, reported in g_O2 g_DW ⁻¹ h⁻¹, are analogous to biomass specific production rate µ (in g_DW h⁻¹ g_DW ⁻¹, or h⁻¹). In his extensive review, Aiba (1982) duly notes that the PI curves reported as µ(I ₀) are calculated from short-term O₂ evolution data, and do not represent growth rates calculated from an exponentially growing algal culture. As stated by Koizumi and Aiba (1980) , and as can be readily derived from Eqs. 7 and 9–11, the specific growth rate µ becomes, under light-limitation, a function of biomass concentration:

$$ \mu= \frac{1}{C}\frac{{dC}}{{dt}} = \frac{{{I_0}}}{C} \cdot {\Phi ^{DW}} \cdot \frac{{{A_C}}}{{{V_C}}} $$

(32)

Photosynthesis-irradiance (PI) curves (Grobbelaar 2006; Grobbelaar et al. 1996; Huesemann et al. 2009; Macedo et al. 1998) can be used to determine the maximum photosynthetic efficiency. Given the culture volume and area exposed to light and the mass of chlorophyll a (Chl a) in the tested culture, the ratio of the reported rate of photosynthesis (in µmol of O₂ evolved mg_{Chl a} ⁻¹ h⁻¹) to the corresponding incident irradiance (in µE m⁻² s⁻¹) can be normalized to yield an apparent efficiency parameter (Ф^APP in mole CO₂ fixed per mole incident photons) as a function of irradiance, with a maximum in the tested range of irradiances. Hence, PI curves can be converted to a Ф^APP(I) curve by plotting the ratio P/I as a function of I, as shown in Fig. 8. As expected, the apparent Ф^APP(I) displays a high initial value at low irradiance (at which all incident photons are absorbed and Ф^APP = Ф^CO2), a decrease due to non-photochemical quenching and, at even higher irradiance, deactivation of the photosystems. Such Ф^APP(I) can be used to determine the range of incident light levels at which the autotrophic yield Ф^DW is maximum or near its maximum for a given algal culture. PI curves, however, are often mistaken for an intrinsic parameter of algal cultures, and inherently depend on culture concentration (Grobbelaar et al. 1996) , physiological state and growth cell geometry. The effective use of PI curves has proven limited by the incomplete report of such parameters. Nevertheless, the general trends displayed in PI curves corroborate that the autotrophic yield is highest at lower irradiance.

Fig. 8

PI curve example: specific rate of photosynthesis (red). Corresponding Ф^APP(I) curve (blue)

4.3 Growth Rate µ and Biomass Yield Ф Do Not Correlate

Algal cultures growth rates are widely used as a strain selection criterion in the field (Shifrin and Chisholm 1981; Sheehan et al. 1998) . However, there is no correlation between the autotrophic biomass yield Ф^DW and the culture maximum growth rate, such that the use of growth rate as a productivity indicator is an erroneous approach. Experimental evidence is shown in Fig. 9. As further support, Wong et al. (2009) theoretically derived that the yield provides an upper bound for growth rate, but does not correlate with it. Consistently, heterotrophs display a trade-off between growth rate and yield , since bacterial metabolism optimizes for both adaptation in the event of sudden stress and biomass formation (Fischer and Sauer 2005) .

Fig. 9

Autotrophic yield Ф^DW reported as P ^MAX (in g_DW m⁻² d⁻¹, according to Eq. 14 at a daily incident PPFD average of 500 µE m⁻² s⁻¹) as a function of maximum growth rate µ _MAX in h⁻¹ calculated in the early exponential phase. Algal cultures grown in sealed nutrient-replete medium supplemented with carbonate and 3 mM nitrate (Holland et al. 2011)

The following analogy may provide a more intuitive understanding. The algal growth rate is defined in the exponential phase under a condition of excess light. This would correspond to feeding fish pellets in excess. Fish A can take a maximum of 4 g pellets per hour, and turn 2 g into biomass, while fish B can take a maximum of 1 g pellets per hour, and turn 1 g into biomass. Cell division occurs when 10 pellets have been processed into biomass. Thus, fish A has a division time of 5 hours, and fish B has a division time of 10 hours. While fish A grows faster than fish B, the biomass yield of fish A (50 % g biomass/ g pellet) is lower than that of fish B (100 %).

5 Target Mixing Conditions and Bioreactor Design

5.1 The PSU Model and Target Photic Zone Velocity

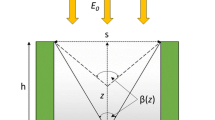
Maximum algal biomass productivity under high outdoor irradiances (1000–2500 µE m⁻² s⁻¹) can only be achieved if the autotrophic yield Ф^DW is near its maximum value. In their development of the PSU model, Camacho-Rubio et al. (2003) integrated kinetics of photoinhibition to more accurately model photosynthetic rates under inhibitory irradiances. As a contrast, the PSU model basis (Eqs. 33–36) is used below to investigate whether, under very high irradiance, mixing conditions can be achieved in order to avoid a decrease in PSII operating efficiency Ф^PSII, which in turn induces a decrease in autotrophic yield Ф^DW [2]. The goal of our model is to determine a target velocity v _T for the alga particle in the photic zone in order to maintain a Ф^PSII near its maximum value. We use two different trajectory models, linear and sinusoidal, which lead to two distinct estimates of v _T: v _{T, L} and v _{T, S} respectively.

Photosynthetic electron transport can be modeled as a two-step kinetic process. First, PSII is excited by light which results in the reduction of the first quinone PSII electron acceptor, Q_A. PSII centers with oxidized Q_A are referred to as ‘open’ while those with reduced Q_A as ‘closed’ (Baker 2008) . The PSII operating efficiency Ф^PSII is a measure of the photon fraction channeled into Q_A reduction. Second, at variable rates on the order of milliseconds (Kroon and Thoms 2006) , the high energy electron from Q_A is transferred to a series of carriers down an electrochemical gradient, which generates ATP and reducing equivalents for biosynthesis. While electron transport in PSI is faster than in PSII, PSI electron transport can be grouped with the slow steps of photosynthesis since PSI is downstream of PSII. An increase in the fraction of closed PSII, which is caused by bottlenecks in the photosynthetic electron transport chain, leads to a decrease in Ф^PSII . Employing a using a simplified PSU kinetic model, and using an experimentally determined incident PPFD at which Ф^DW or Ф^PSII starts to decrease, we derive an expression for the threshold fraction of closed PSII above which NPQ is considered significant. Alternatively, this threshold fraction of closed PSII can be directly measured by fluorescence response . With these simplifying assumptions, this threshold fraction is used to determine the alga speed across the photic zone , as an indicator of agitation conditions, which can maintain a fraction of open PSII conducive to a maximum Ф^PSII.

The PSII centers exist as closed PSII (A⁻) and open PSII (A):

$$\text{A}+\text{h }\!\!\nu\!\!\text{ }\to {{\text{A}}^{-}}\left( \text{ratek}\ {{k}_{\text{1}}}\text{in}\ {{\text{s}}^{-}}^{1} \right)$$

(33)

$${{\text{A}}^{-}}\to \text{REC}+\text{A }\left( \text{rate}\,{{k}_{\text{2}}}\ \text{in }{{\text{s}}^{-}}^{1} \right)$$

(34)

where REC designates the pool of reduced carriers downstream of Q_A.

$$ {a_0} = a + {a^ - } $$

(35)

where a ₀, a, a ⁻ are respectively total, open and closed PSII concentration in the culture (in mol_PSII).

Under low light, we assume that the fraction of closed PSII remains low enough not to induce saturation kinetics in the slow step, and that the concentration of A⁻ is quasi-steady:

$$ \frac{{d{a^ - }}}{{dt}} = 0 = {k_1}( x ) \cdot ( {{a_0} - {a^ - }} ) - {k_2} \cdot {a^ - } $$

(36)

The following expression for k ₁ which is analogous to that given in Camacho Rubio et al. (2003) , was modified to display Beer-Lambert’s law and Ф^PSII, and account for the photon flux splitting between the PSI and PSII. Assuming that an equal number of PSI and PSII absorb the incident light at an equal rate (factor ½):

$$ {k_1}( x ) = {\Phi ^{PSII}} \cdot \frac{{{I_0} \cdot {{10}^{ - 6}}}}{2} \cdot \frac{{{\sigma ^{DW}}}}{F} \cdot \exp ( { - {\sigma ^{DW}} \cdot C \cdot x} ) $$

(37)

where x is the distance (in m) from the light incidence surface; Ф^PSII is in moles excited PSII per Einstein absorbed; I ₀ is the absorbed PPFD in µE m⁻² s⁻¹; σ^DW is the scatter-corrected algal cross section in m² g_DW ⁻¹ (Sect. 2.2); C is the biomass concentration in g_DW m⁻³; F is the fraction of PSII in mol_PSII g_DW ⁻¹, determined experimentally (Falkowski et al. 1981; Cunningham et al. 1990) . While the time constant of Q_A reduction is on the order of nanoseconds, the rate of exciton formation k ₁ depends on the incident light intensity as shown by Eq. 37. Under the high irradiance of 3400 µmol m⁻² s⁻¹, Lazar and Pospisil (1999) estimated this rate to be 5500 s⁻¹. Using the example values in Table 3, Eq. 37 evaluates k ₁ as 2900 s⁻¹, which is on the same order.

Table 3 Example parameters for calculation of the threshold closed reaction fraction (last row) for Dunaliella tertiolecta

At a threshold irradiance I _T (µE m⁻² s⁻¹), Ф^PSII (and therefore Ф^DW) starts to decrease significantly due to NPQ . This arbitrarily defined I _T threshold value corresponds to the maximum acceptable loss in productivity. I _T can be determined from PI curve data (Sect. 3.2). Alternatively, fluorescence response can be used to measure the decrease in Ф^PSII with increasing incident PPFD (Baker 2008; Kramer et al. 2004; Campbell et al. 1998; Schreiber 2004) . Combining Eqs. 36–37, and taking x = 0 (point of maximum irradiance), the corresponding threshold fraction of excited centers (1-q _L )_T is given by:

$$ {( {1 - {q_L}} )_T} = {\left. {\frac{{{a^ - }}}{{{a_0}}}} \right|_T} = \frac{1}{{1 + \frac{{{k_2}}}{{{k_1}( 0 )}}}} = \frac{1}{{1 + \frac{{2F \cdot {k_2}}}{{{\Phi ^{PSII}} \cdot {I_T} \cdot {{10}^{ - 6}} \cdot {\sigma ^{DW}}}}}} $$

(38)

The determination of this threshold value is highly sensitive to the choice of k ₂. Due to the complexity of the electron transport mechanisms involved in channeling PSII electrons, we choose the rate of the slowest PSII step, as the slowest step will be the first responsible for an increase in a−. Using the rates published by Kroon and Thoms (Kroon and Thoms 2006) , and noting that these values highly underestimate the rate of PSII charge recombination (de Wijn and van Gorkom 2002) , we evaluate k ₂ as the slower average electron transfer rate between Q_A and Q_B (k ₂ = 153 s⁻¹). This rate can also be estimated experimentally from determination of the ‘turnover time’ (Dubinsky et al. 1986) . An example calculation is presented for Dunaliella tertiolecta (Table 3). The calculated threshold (maximum desired excited fraction) is 25 % for D. tertiolecta (Table 3), consistent with published fluorescence response trends. Fluorescence response, which can directly measure the fraction of closed PSII (1-q _L) along with Ф^PSII under increasing irradiance (Baker 2008; Kramer et al. 2004; Campbell et al. 1998) , can alternatively be used to determine experimentally both I _T and the threshold (1-q _L) value. An added benefit of this method is the ability to estimate k ₂ from Eq. 38 for further use in the estimation of target mixing velocities.

Qualitative insights can be derived from the simplified PSU model as follows. Subjecting the algal culture to a given irradiance I _T constrains the fraction of open centers q _L as well as the PSII operating efficiency Ф^PSII, as seen in Fig. 7, such that a resulting correlation between Ф^PSII and q _L can be established (Fig. 10a). This correlation can be used in Eq. 38 to solve for Ф^PSII as a function of the limiting kinetic rate k ₂, the scatter-corrected algal cross-section σ^DW, or the concentration of excitable PSII centers F (Fig 10b, c and d). As expected, the PSII operating efficiency Ф^PSII increases with k ₂, and F, and decreases with σ^DW. Regarding the latter, a reduced number of Chl a per PSII (or antenna size) leads to a decrease in σ^DW, which in turn reduces the flux of absorbed photons per cell. Accordingly, genetic mutants with a reduced antenna size (reduced number of Chlorophyll per PSII) have been shown to enable greater biomass productivity under high irradiance (Huesemann et al. 2009; Beckmann et al. 2009) .

Fig. 10

Variation of Ф^PSII as a function of various parameters. a Rough correlation between the fraction of open centers q _L and Ф^PSII. b Increase of Ф^PSII as a function of the k ₂ kinetic parameter. c Decrease of Ф^PSII as a function of the scatter-corrected algal cross-section σ^DW. d Increase of Ф^PSII as a function of the concentration of PSII centers F

Under elevated outdoor light levels, the A⁻ pool is no longer quasi-steady. Adequate agitation can render the system essentially bi-phasic (Merchuk et al. 2007) , in which the concentration of A⁻ oscillates between low and high levels as the cell moves between dark and light zones. In the general case, for which an alga trajectory x(t) is known, Eq. 36 becomes

$$ \frac{{d{a^ - }}}{{dt}} + [ {{k_1}[ {x( t )} ] + {k_2}} ] \cdot {a^ - } = {k_1}[ {x( t )} ] \cdot {a_0} $$

(39)

Solving this first order ODE for a ⁻(t) in the general case requires integrating factor u(t):

$$u\left( t \right)=\exp \left\{ \int\limits_{0}^{t}{\left[ {{k}_{1}}\left[ x\left( {{t}'} \right) \right]+{{k}_{2}} \right]dt'} \right\}$$

(40)

Assuming the known trajectory x(t) starts in the dark zone, such that a ⁻(0) = 0, the fraction of closed PSII centers after time t in the photic zone is:

$$\frac{{{a}^{-}}\left( t \right)}{{{a}_{0}}}=\frac{1}{u\left( t \right)}\cdot \int\limits_{0}^{t}{u\left( {{t}'} \right)\cdot {{k}_{1}}\left[ x\left( t' \right) \right]dt'}$$

(41)

The height of the photic zone is arbitrarily defined as the depth at which 99 % of the incident light is absorbed by the biomass of concentration C:

$$ d = \frac{{\ln ( {100} )}}{{{\sigma ^{DW}} \cdot C}} $$

(42)

As an example, a Dunaliella culture (Table 3) at a concentration of 2 g L⁻¹ has a penetration depth of 1.2 cm.

In a simple linear-trajectory case, the target speed v _{T, L} can be calculated as follows. We assume that the alga particle travels at a constant speed v _{T, L} from the dark zone (x = d) to the surface (x = 0), and back to the dark zone. For each cycle the alga particle spends time 2τ in the photic zone such that

$$ \tau= \frac{d}{{{\nu _{T,L}}}} $$

(43)

An implicit equation for the target speed v _{T, L} can be obtained by substituting a linear trajectory into Eq. 41, with a constraint that half the threshold PSII fraction is excited during one half cycle (0 ≤ x ≤ d) of the photic zone trajectory:

$$\frac{1}{2}{{\left. \frac{{{a}^{-}}}{{{a}_{0}}} \right|}_{T}}=\frac{1}{{{u}_{L}}\left( \tau \right)}\cdot \int\limits_{0}^{\tau }{{{u}_{L}}\left( {{t}'} \right)\cdot {{k}_{1}}\left( {{\nu }_{T,L}}\cdot t' \right)dt'}$$

(44)

where

$${{u}_{L}}\left( t \right)=\exp \left\{ \int\limits_{0}^{t}{\left[ {{k}_{1}}\left[ {{\nu }_{T,L}}\cdot t' \right]+{{k}_{2}} \right]dt'} \right\}$$

(45)

One numerically adjusts v _{T, L} until Eq. 44 is satisfied.

A more realistic approximation is that the alga particle follows a sinusoidal trajectory with a target speed v _{T, S}. For purposes of discussion we assume the dark zone has the same thickness d as the photic zone, and that the period in which the alga occupies each zone is 2τ. At t = 0, the particle enters the photic zone from the dark zone and a ⁻(0) = 0. The sinusoidal trajectory is

$$ {x_S}( {t,\tau } ) = d\left[ {1 - \sin \left( {\frac{\pi }{{2\tau }}t} \right)} \right] $$

(46)

As with the linear case above, time τ can be calculated from an implicit equation:

$${{\left. \frac{{{a}^{-}}}{{{a}_{0}}} \right|}_{T}}=\frac{1}{{{u}_{S}}\left( 2\tau ,\tau \right)}\cdot \int\limits_{0}^{2\tau }{{{u}_{S}}\left( t',\tau \right)}\cdot {{k}_{1}}\left[ {{x}_{S}}\left( t',\tau \right) \right]dt'$$

(47)

where

$${{u}_{S}}\left( t,\tau \right)=\exp \left\{ \int\limits_{0}^{t}{\left[ {{k}_{1}}\left[ {{x}_{S}}\left( t',\tau \right) \right]+{{k}_{2}} \right]dt'} \right\}$$

(48)

With τ in hand, the corresponding target speed v _{T, S} can be estimated as the root-mean-square velocity of the alga particle in the photic zone:

$$ {\nu _{T,S}} = \frac{{\pi d}}{{2\sqrt {2\tau } }} \approx 1.11\frac{d}{\tau } $$

(49)

The Mathcad program used to calculate v _T (linear and sinusoidal models) is provided in Holland and Wheeler (2011) . The dependence of the target velocity v _T on the biomass concentration C and the culture extinction coefficient σ^DW is due to that of d (Eq. 42) and k ₁ (Eq. 37).

Calculated values of v _{T, L} and v _{T, S} represent upper and lower bounds, respectively, for the desired average algal particle speed, as the linear model does not account for the ‘turn-around’ time at the light incidence surface, while the sinusoidal model likely overestimates it. Given a velocity v _T on the order of v _{T, L} to v _{T, S} across the photic zone , an alga particle effectively avoids over-excitation of the PSII system and a resulting decrease in quantum efficiency Ф^PSII. Subsequently, a dark phase on the order of 50–100 ms suffices to relax the PSII to a mostly open state (Nedbal et al. 1999) .

Target velocities v _{T, L} and v _{T, S} were calculated for Dunaliella tertiolecta as a function of biomass concentration (Fig. 11), using the values listed in Table 3. Two incident irradiance values are used: a high value I ₀ of 1000 µE m⁻² s⁻¹ and the highest possible solar irradiance I _H. Incident solar energy before atmospheric scattering is 1387 W m⁻² (Thuillier et al., 2003) , which converts to I _H = 2538 µE m⁻² s⁻¹ using the conversion factor 1.83 µE J⁻¹ (Table 2).

Fig. 11

Calculation of target velocities v _T (m s⁻¹) using the linear model (v _T,L) and the sinusoidal model (v _T,S). Velocities were calculated as a function of culture concentration C (g L⁻¹) for the high solar irradiance I ₀ (1000 µE m⁻² s⁻¹) and the highest possible direct normal solar irradiance I _H (2500 µE m⁻² s⁻¹) for Dunaliella tertiolecta (parameter values from Table 3)

5.2 Target Velocity and Bioreactor Design

The high biomass densities required under high illumination (Fig. 11, 5–10 g_DW L⁻¹) also set constraints on the nutrients feed concentration (Sect. 5.2). The very high calculated speeds (Fig. 11) in the photic zone in order to avoid a decrease in Ф^PSII are consistent with the well-documented ‘flashing light’ effect, which shows an increase in photosynthesis when light is pulsed at high frequency (Grobbelaar et al. 1996) . Indeed, the calculated high target speeds correspond to residence times on the order of 0.6–1 ms at I ₀ and 0.23–0.37 ms at I _H, using the sinusoidal and linear models for the lower and upper bounds, respectively. In effect, such agitation, equivalent to LD cycles on the order of milliseconds, should extend the linear range of PI-curves to very high incident PPFD, which is what Nedbal et al. (1996) observed experimentally. While Nedbal et al. (1996) linked the flash-induced growth enhancement to a pool exhaustion along the electron transport chain (namely the PQ pool), the present work additionally provides a simple mathematical model to estimate a target speed as a key design parameter.

Actual fluid velocity perpendicular to the light incidence surface, which can be measured using radioactive particle tracking (Luo et al. 2003) or a conductivity probe (impulse-response technique (Gluz and Merchuk 1996)) , usually range in the 5–40 cm s⁻¹ for tubular reactors. While tubular reactors present the advantage of a closed axenic environment, desirable for the synthesis of high value added products, and lower mixing velocities, better suited for culturing shear-sensitive diatoms (such as Porphyridium sp. and P. tricornutum) (Thomas and Gibson 1990) , they are not able to achieve mixing velocities capable of averting photon dissipation under high outdoor irradiances. The above calculations call for a fundamental change in reactor design for algal cultivation under high irradiance, in order to reach velocities on the order of 5–20 m s⁻¹ in the photic zone (~ 2 cm or less). Green algae (Chlorophyceae) have been shown to display highest resistance to shear (Thomas and Gibson 1990) , but additional selection strategies may need to be designed given such high estimated speeds. As an encouraging result, Barbosa et al. (2004) showed that sparger maximum bubble velocities on the order of 1–20 m s⁻¹ did not cause lethal shear to the green-algae Dunaliella tertiolecta and Chlamydomonas reinhardtii .

In this work, simple linear and sinusoidal functions were used to simulate the light/dark cycles which the algal cells are exposed to. At the high modeled target speeds, the turbulent fluid flow would be more accurately modeled using computational fluid dynamics (Luo and Al-Dahhan 2011) . Alternatively, the random character of light/dark cycles can be captured experimentally using computer-automated radioactive particle tracking (CARPT) techniques (Luo et al. 2003; Luo and Al-Dahhan 2004) . CARPT provides a invaluable means to fully characterize novel turbulent algal bioreactor designs. In addition, the proposed model can be further refined by incorporating a more sophisticated mechanistic description of photosynthesis (Lazar and Pospisil 1999; Lazar 2003; Lazar 2006) , with identification and estimation of key kinetic parameters.

Microalgae , macroalgae and plants all can achieve quantum yields close to the theoretical maximum of 0.125 mol CO₂ fixed (or mol O₂ evolved) per mol photons absorbed. Plants such as Flaveria spp. can achieve a Ф^O2 on the order of 0.108 (Lal and Edwards 1995) , macroalgae on the order of 0.08 (Frost-Christensen and Sand-Jensen 1992) , and microalgae a Ф^CO2 on the order of 0.106 (Welschmeyer and Lorenzen 1981) . However, only microalgae can achieve high frequency turnover in the photic zone , which is crucial to maximize utilization of a continuous source of incident light. Despite the relative ease of harvest of plants and macroalgae , their static nature prevents dark relaxation under high irradiance outdoor conditions. Therefore, under appropriate mixing conditions, microalgae are best suited to achieve area productivity reflecting these measured maximum quantum yields (or autotrophic yields).

5.3 Proposed Bioreactor Design

The following algal bioreactor design (Fig. 12) fulfills the various criteria described above. At steady-state, reactor depth and biomass concentration allow for full absorption of the incident light (Sect. 2.1) as well as a dark zone for Light Dark cycling (Sect. 4.1). Sparging high velocity air a few centimeters below the surface creates adequate mixing in the photic zone and averts photoinhibition in an open pond configuration under high irradiance. The shallow water column between air sparging and the free surface of the pond would allow to reduce power consumption and yet effect high Light Dark frequencies. This sparging would provide a fraction of the CO₂ required for growth. Under high irradiance, CO₂ could be supplemented as a concentrated gas stream (coming from AD biogas combustion) at or near the bottom of the pond, sufficiently lower than the air sparging zone to avoid CO₂ stripping and maximize CO₂ dissolution. This is consistent with the fact that, by design, the light-activated cells would carry out the slow steps of photosynthesis and carbon fixation in the dark zone. N and P nutrients should be supplemented as a liquid stream at a depth which should be optimized: the effective local nutrient concentration, which depends on the feed characteristics and reactor mixing, will affect the algal physiology.

Fig. 12

Proposed bioreactor design

Since the high rate air sparging occurs at a fixed depth, bioreactor level management becomes crucial, such that make-up water and feed flow rates need to match the flow rate of the continuously harvested algal biomass (see Sect. 5 for details). The presence of a shield may help reduce water evaporation by creating a high humidity air zone above the pond, and allow for rainwater collection for storage and recycling. In addition, the sparged air may need to be pre-humidified to reduce evaporative losses.

The much debated addition of a temperature control system depends on the pond geographic location and the degree of processing achieved on-site. Combined Heat and Power generation from the AD biogas would contribute heat, while underground water storage would provide cooling. Pond depth helps provide an additional buffering mechanism for temperature regulation. Importantly, efficient conversion of the incident light into biomass (through photochemical quenching) reduces the temperature increase due to radiation seen in otherwise poorly mixed ponds under elevated irradiance.

Design optimization entails increasing high rate air sparging in order to restore maximum biomass yield under increasing light levels. Such optimization could be facilitated by the use of chlorophyll fluorescence quenching analysis (Sect. 3.1) by sampling algae at different pond locations. Under continuous operation, air sparging rates would then become dependent upon the measured incident light levels.

6 Bioreactor Parameterization and Strategy to Achieve High Lipid Production

6.1 Poor Mixing Conditions: Fish Tank Analogy

Under condition of poor mixing and elevated irradiance (saturating and/or inhibitory), the simple model presented in this work (Sect. 2.1 and Eq. 30) no longer fully describes algal biomass production, such as for tubular reactors or raceway ponds subjected to irradiances over 1000 µE m⁻² s⁻¹, and as can be inferred from the velocity modeling results in Sect. 4. Provided well-defined geometries for the PI experimental chamber and the modeled reactor, PI curves provide critical information which can be used as described below.

As a possible approach, poorly-mixed reactors can be theoretically divided into 4 zones, the location of which depends on the reactor geometry, the incident PPFD I ₀, the scatter-corrected culture extinction coefficient σ^DW (in m² g_DW ⁻¹), the distance x from the light incidence surface, the area perpendicular to the light source A _C in m² and the algal biomass concentration C. In order to help understanding, a fish-tank analogy is provided (Fig. 13): the fish are swimming horizontally and are circumscribed to a given depth x; the constant and elevated PPFD is represented by a high rate supply of fish food; in zone 1, the overfed fish divide more slowly than their well-fed counterpart in zone 2; all the food entering zone 3 is taken-up by the fish such that the fish biomass production is proportional to the food intake; all pellets have been utilized in zones 1-3 such that zone 4 does not support fish growth.

Fig. 13

Fish-tank analogy describing poorly mixed algal bioreactors under high irradiance (no vertical mixing). Q_A reduction is represented by a pellet in the fish mouth; the slow steps of photosynthesis, which correspond to an energy transfer from Q_A down the electrochemical gradient, are represented by a pellet in the fish stomach. Photoinhibited algal cells are represented by grey fish with two pellets in their stomach

Correspondingly, for the sake of simplicity in the discussion below, the zones are taken to be 1D strata. Zone 1 is closest to the light incidence surface (x = 0), with Zones 2 and onward corresponding to increasing values of x. The location of these zones is well defined when mixing is poor, allowing for a quasi steady-state approximation which circumscribes an algal particle to an infinitesimal volume with a defined PPFD . The upper-most region (zone 1) undergoes photoinhibition , which corresponds to a specific growth rate lower than its maximum values; in zone 2, the light-excess region supports exponential growth at µ _MAX; in zone 3, the light-limited region supports a linear biomass increase; zone 4 light levels are too low to support biomass production. At a specified dilute biomass concentration C _PI and PI chamber geometry (assumed planar), PI curves (Macedo et al. 1998) can be parameterized to satisfactorily describe growth behavior in zones 1 and 2, as well as the transition point between zones 2 and 3. This transition between light excess and light limitation occurs at the threshold depth x _T (in m).

As currently modeled in the literature (Yun and Park 2003) , the local volumetric production rate $P_{1 - 2}^V$ (in g_DW m⁻³ h⁻¹) in zones 1 and 2 (0 < x < x _T) is

$$ P_{1 - 2}^V( x ) = {\mu _{PI}}( x ) \cdot C $$

(50)

where, µ _PI depends on the depth-dependent PPFD I(x), which follows the Beer-Lambert law provided correction for scatter (Sect. 2.2):

$$ I( x ) = {I_0} \cdot \exp ( { - {\sigma ^{DW}} \cdot C \cdot x} ) $$

(51)

The algal biomass production P _1-2 (in g_DW h⁻¹) in zones 1-2 is:

$$ {P_{1 - 2}}( x ) = C \cdot {A_C}\int\limits_0^{{x_T}} {{\mu _{PI}}( x )dx}$$

(52)

At a threshold irradiance I _T, the ratio of the specific growth rate over the irradiance starts to decrease with increasing incident PPFD, reflecting a decrease in autotrophic yield (discussed in Sect. 4.1). This corresponds to a threshold specific energy flux (EF _T, in µE g_DW ⁻¹ h⁻¹):

$$ E{F_T} = \frac{{{I_{ABS,T}}}}{{{C_{PI}} \cdot {L_{PI}}}} = \frac{{{I_T} \cdot [ {1 - \exp ( { - {\sigma ^{DW}} \cdot {C_{PI}} \cdot {L_{PI}}} )} ]}}{{{C_{PI}} \cdot {L_{PI}}}} $$

(53)

where C _PI is the algal biomass concentration (in g_DW m⁻³) in the PI chamber, L _PI is the depth of the chamber (in m). At low biomass concentration and chamber thickness,

$$ E{F_T} \to {I_T} \cdot {\sigma ^{DW}} $$

(54)

The EF _T can also be solved from the batch growth concentration at which the ELT occurs.

In the reactor, the specific energy flux EF(x) (in µE g_DW ⁻¹ h⁻¹) is related to the decrease in transmitted radiation:

$$ EF( x ) = \frac{{dI( x )}}{{dx}} \cdot \frac{1}{C} = {\sigma ^{DW}} \cdot {I_0} \cdot \exp ( { - {\sigma ^{DW}} \cdot C \cdot x} ) $$

(55)

such that x _T can be solved algebraically using Eqs. 53 and 55 by setting

$$ E{F_T} = EF( {{x_T}} ) $$

(56)

In the event of negligible biomass maintenance in zone 4, integration over depth yields the following productivity in zones 3–4 P _3-4(in g_DW h⁻¹):

$$ {P_{3 - 4}} = \int\limits_{{x_T}}^\infty{{\Phi ^{DW}} \cdot {A_C} \cdot C \cdot EF( x )dx}$$

(57)

Assuming a constant autotrophic yield Ф^DW in zone 3 yields:

$$ {P_{3 - 4}} = {A_C} \cdot {\Phi ^{DW}}{I_0} \cdot \exp ( { - {\sigma ^{DW}} \cdot C \cdot {x_T}} ) = {A_C} \cdot {\Phi ^{DW}} \cdot I( {{x_T}} ) $$

(58)

In the event of non-negligible maintenance energy in the dark, a threshold depth between zones 3 and 4 can be derived analogously to x _T.

Importantly, NPQ photon dissipation in zones 1 and 2 limits maximization of the bioreactor productivity. Additionally, photoinhibition necessitates additional recovery time (Wu and Merchuk 2001) which in turn may impair the autotrophic yield Ф^DW in zones 1-3. As discussed in Sect. 4, vigorous mixing allows one to bypass such complex analysis and maximize productivity. The corresponding fish tank analysis is shown in Fig. 14.

Fig. 14

Fish-tank analogy describing the well-mixed counterpart to Fig. 13 (excellent vertical mixing)

6.2 Bioreactor Parameterization Under Vigorous Mixing

As an example of simple geometry (Fig. 15), we consider a planar bioreactor (such as an outdoor pond) illuminated from one side with an incident PPFD I ₀, of culture volume V _C (m³) and area A _C (m²) normal to the light source. A nutrient feed stream (such a N or P) is supplied to the reactor at a concentration S ₀ (g_S m⁻³) and a volumetric flow rate F _IN (in m³ h⁻¹), with a concentration S (g_S m⁻³) in the reactor such that S ≪ S ₀ . The algal culture at a concentration C is drawn out of the reactor at volumetric flow rate F _OUT (in m³ h⁻¹). The biomass yield on the substrate Y _C/S (in g_DW g_S ⁻¹) is constant (Blanch and Clark 1997) . Assuming that I ₀ is low enough to support maximum yield photosynthesis at the surface of light incidence, Eq. 30 can be used to estimate the rate of photosynthesis P(I ₀ ,C, L) in g_DW m⁻² h⁻¹ as:

Fig. 15

Bioreactor parameters

$$ P( {C,{I_0},L} ) = {\Phi ^{DW}} \cdot {I_0} \cdot [ {1 - \exp ( {{\sigma ^{DW}} \cdot L \cdot C} )} ] $$

(59)

In this case, the following general conservation equations (Blanch and Clark 1997) hold for any type of reactor (batch, fed-batch in the substrate S, or chemostat) and whether the light is partially or fully absorbed by the algal biomass:

$$ \frac{{d( {S \cdot {V_C}} )}}{{dt}} = {S_0} \cdot {F_{IN}} - S \cdot {F_{OUT}} - \frac{{{A_C}}}{{{Y_{C/S}}}}P( {C,{I_0},L} ) $$

(60)

$$ \frac{{d( {C \cdot {V_C}} )}}{{dt}} =- C \cdot {F_{OUT}} + {A_C} \cdot P( {C,{I_0},L} ) $$

(61)

where t is the duration (in h) of growth under light.

In the example of a chemostat (F _CHEM = F _IN = F _OUT) of initial biomass concentration C ₀, solving Eqs. 59–60 at constant S, V _C and C, and taking S ≪ S ₀ constrains the nutrients feed concentration to:

$$ {S_0} = \frac{{{C_0}}}{{{Y_{C/S}}}} $$

(62)

and, solving Eq. 61, the corresponding volumetric flow rate F _CHEM is,

$$ {F_{CHEM}} = {A_C}\frac{{P( {{C_0},{I_0},L} )}}{{{C_0}}} $$

(63)

For variable irradiance I ₀(t), the volumetric flow rate F _CHEM(t) can be adjusted so as to maintain a constant S, V _C and C. In the event of an inhibitory light level I ₀ for which the autotrophic yield is not maximum, the biomass concentration C and culture depth L can be increased to ensure not only full absorption of the incident light, but also the presence of a dark zone. Under such condition, as detailed in Sect. 4, vigorous mixing conditions enable the use of Eqs. 59–61 to parameterize the reactor, and Eq. 59 to estimate the rate of biomass production P.

6.3 Lipid Accumulation Strategy

Growth arrest in batch culture has been the only reported means of achieving a nitrogen starvation conducive to lipid accumulation (discussed in Sect. 1.1). The parameterization presented above provides a method to accomplish it under steady-state conditions. Algal lipid accumulation in batch culture under nitrogen limitation effectively corresponds to an excess flux of light quanta compared to the rate of nitrogen taken-up. Under nitrogen excess, the algal biomass exhibits a steady-state nitrogen weight fraction (or nitrogen quotient) Q _N (in g_N g_DW ⁻¹), which is the inverse of the yield on nitrogen Y _C/N (in g_DW g_N ⁻¹), where:

$$ {Q_N} = \frac{1}{{{Y_{C/N}}}} $$

(64)

At a given irradiance, lowering the nitrogen feed concentration S ₀ effectively lowers the nitrogen quotient Q _N due to the constraint in Eq. 62, or:

$$ {Q_N} = \frac{{{S_0}}}{{{C_0}}} $$

(65)

In turn, lowering the nitrogen quotient of the biomass will lead to a lowering of the autotrophic yield Ф^DW . As discussed in Sect. 1.1, the sole augmentation in the biomass lipid fraction increases the specific energy of the biomass, and hence decreases the autotrophic yield assuming that the metabolic energy efficiency remains unchanged under N-limitation. In all likelihood, a trade-off between lipid content and metabolic efficiency will further lower the autotrophic yield upon nitrogen limitation. The lowered autotrophic yield needs to be evaluated using Eq. 60 from a transient decrease of biomass concentration C over time, assuming all other parameters are maintained at their nutrient replete value. Alternatively, the Ф^DW(S ₀) can be established from C(t) by running the reactor in fed-batch mode, by shutting the effluent. Assuming all incident light is absorbed, Eq. 60 becomes:

$$ {V_C}\frac{{dC}}{{dt}} + C \cdot {F_{IN}} = {A_c} \cdot {\Phi ^{DW}}( {{S_0}} ) \cdot {I_0} $$

(66)

Nevertheless, the operating condition Ф^DW(S ₀) can be optimized for each algal culture so as to reach the greatest continuous lipid productivity P _LIPIDS (in g_LIPIDS h⁻¹) as:

$$ {P_{LIPIDS}}( {{S_0}} ) = {A_c} \cdot {\Phi ^{DW}}( {{S_0}} ) \cdot {I_0} \cdot {F_{LIPIDS}}( {{S_0}} ) $$

(67)

The ability to achieve continuous lipid production under fed-batch or chemostat mode remains to be demonstrated. The following batch results (Fig. 16) provide encouraging evidence to this possibility. Ammonium depletion (Fig. 16a) occurring at an early stage during growth did not show a significant slowdown in growth rate (Fig. 16b). Hence, the nitrogen quotient can be significantly lowered from its nutrient replete value and still support good growth. The chlorophyll content correlated with the nitrogen quotient (Fig. 16c), such that biomass with a lower Q _N displays a reduced antenna size, which is associated with a lower σ^DW and a higher Ф^DW (discussed in Sect. 4.1). Finally, lipid content at the onset of nitrate starvation in batch cultures showed a significant increase in lipid content (Fig. 16d).

Fig. 16

Onset of nitrogen limitation. a Ammonium depletion in the culture medium upon algal growth in batch. b Growth curves corresponding to the ammonium uptake shown in a. c Correlation between chlorophyll content and nitrogen quotient upon ammonium depletion for the cultures shown in a. d Increase in lipid content at the onset of nitrate limitation. Growth conditions using sealed carbonate addition and culture identity (1–13 correspond to Cs, Ds, Es, C, E, SE, MON, Pr5, FRA, E1, Pr8, Pr9, Pr10 respectively) are detailed in Holland and Wheeler (2011)

7 Concluding Remarks on Modeling Bioreactors in the Literature

Advanced control algorithms have been developed in view of controlling algal growth in bioreactors. The growth models usually followed Monod saturation kinetics , developed by Droop (1973) for algae, which assumed a limiting nutrient but did not account for light. In these complex models, light energy was either assumed in excess or not mentioned (Bernard and Gouzé 1999; Surisetty 2009; Mailleret et al. 2005; Rusch and Malone 1998; Takache et al. 2009) .

Generally, characterization of algal bioreactor productivity hinges on the determination and modeling of the culture specific growth rate µ. The stated or underlying assumption is that the bioreactor productivity P _BIOREACTOR (in g_DW m⁻³ h⁻¹) follows a law of the form (Hu et al. 2012; Mailleret et al. 2005; Barbosa et al. 2003a; Vunjak-Novakovic et al. 2005; Hall et al. 2003; Molina et al. 2001; Bernard and Gouzé 1999) :

$$ {P_{BIOREACTOR}} = \frac{{dC}}{{dt}} = \mu\cdot C $$

(68)

where µ(I) follows a saturation kinetics described by Photosynthesis-Irradiance (PI) curves (Macedo et al. 1998; Hu et al. 2012; Molina et al. 2001) .

Photosynthesis-Irradiance (PI) curves are obtained by using an algal culture of fixed concentration, such that the biomass-concentration dependency discussed Sect. 3.2 does not lead to any noticeable model discrepancies when parameters are fitted (Macedo et al. 1998) . However, the resulting µ(I) derived from a PI-curve does not describe biomass growth in a bioreactor over an extended period of time, assuming light-limitation is reached, as remarked by Yun and Park (2003) . The mechanistic PSU model, thoroughly reviewed and further developed by Camacho-Rubio et al. (2003) , was used to account for photoinhibition processes and ‘flashing light effects’ in predicting rates of photosynthesis as a function of irradiance. As expected from this analysis, the PI-curve approach was satisfactory to predict specific growth rates at high rates (under high light) but deviated significantly from experimental data at low rates (Fig. 13 in Camacho Rubio et al. (2003)) . Hence, the direct use of PI curves should only be limited to regions of light excess, in which the algal growth follows an exponential behavior.

As discussed in Sect. 2.1 and Sect. 5.1, biomass production follows such a law (Eq. 68) only under conditions of light excess, since under light limitation the bioreactor productivity becomes independent of the algal biomass concentration C. Equivalently, under conditions of complete light absorption by the bioreactor, the specific growth rate µ becomes dependent upon the biomass concentration C (Eq. 32). As shown in Sect. 3, bioreactors in which light excess is stated (Rusch and Malone 1998) or implied through the use of Eq. 68 do not function optimally, since photons are lost as either passing through the culture or dissipated through non-photochemical quenching . In the case of poorly mixed bioreactors which display both a light excess and a light-limited region, Eq. 68 does not describe biomass production (Sect. 5.1). Hence, parameterization and determination of algal culture specific growth rates µ either provide an erroneous description of biomass productivity, or an accurate description of a bioreactor displaying sub-optimal productivity.

Hence, to-date, the inability to robustly account for algal biomass production rate under light-limitation as well as light-excess has prevented the derivation of a satisfactory mass balance for the simple parameterization of bioreactors. The methodology presented here fully resolves this shortcoming.