Adaptive Control System for Solution of Fault Tolerance Problem

Abstract

Adaptive control can provide desirable behavior of a process even though the process parameters are unknown or may vary with time. Conventional adaptive control requires that the speed of adaptation must be more rapid than that of the parameter changes. However, in practice, problems do arise when this is not the case. For example, when fault occurs in a process, the parameters may change very dramatically. A new approach based on simultaneous identification and adaptation of unknown parameters is suggested for compensation of rapidly changing parameters. High dynamic precision adaptive control can be used for the solution of a fault tolerance problem in complex and multivariable processes and systems.

15.1 Determination of a Mathematical Model of a Process

A mathematical model of a process on a stationary regime can be found from the sequence of Markov parameters using the classical Ho algorithm [1]. The Markov parameters can be obtained from input–output relationships or more directly as an impulse response of the system. It is well known that according to the theorem of Kronecker the rank of the Hankel matrix constructed from the Markov parameters is equal to the order of the system from which the parameters are obtained. Therefore, by consistently increasing the dimension of the Hankel matrix Γ until

$$ {\text{rank}}\;\Upgamma_{r} = {\text{rank}}\;\Upgamma_{r + 1} $$

the order of the system can be obtained as equal to r. However, in practical implementation, this rank-order relationship may not give accurate results due to several factors: sensitivity of the numerical rank calculation and bias of the rank if information about the process is corrupted by noise. This problem can be avoided using singular value decomposition (SVD) of the Hankel matrix:

$$ \Upgamma = {USV}^{T} , $$

(15.1)

where

$$ U^{T} U = V^{T} V = I, $$

$$ S = diag(\sigma_{1} ,\sigma_{2} , \ldots ,\sigma_{l} ,\sigma_{l + 1} , \ldots \sigma_{n} ). $$

Here U and V are orthogonal matrices. The diagonal elements of the matrix S (the singular values) in (15.1) are arranged in the following order $\sigma_{1} > \sigma_{2} > \cdots > \sigma_{n} > 0$. Applying the property of SVD to reflect the order of a system through the smallest singular value, the order of the system can be determined with the tolerance required. From practical point of view a reduced order model is more preferable. Taking into account that the best approximation in the Hankel norm sense is within a distance of $\sigma_{l + 1}$, the model of order l can be found. However, a relevant matrix built from Markov parameters of this reduced order model should also be of the Hankel matrix. But it is not an easy matter to find such a Hankel matrix for the reduced order process. A simpler solution, although theoretically not the best, can be found from the least squares approximation of the original Hankel matrix [2–4]. The discrete time state-space realization of the process can be determined from the relationship between Markov parameters and representation of the Hankel matrix through relevant controllability and observability matrices of the process:

$$ \Upgamma = \left[ {\begin{array}{*{20}c} {C_{d} } \\ {C_{d} A_{d} } \\ {C_{d} A_{d}^{2} } \\ . \\ . \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {A_{d} } & {A_{d} B_{d} } & {A_{d}^{2} B_{d} } & . & . \\ \end{array} } \right] = \Upomega {\rm E}, $$

(15.2)

where

• $A_{d}$ is the system matrix,

• $B_{d}$ is the control matrix,

• $C_{d}$ is the output matrix,

• Ω is the observability matrix,

• E is the controllability matrix.

15.2 The Adaptive Control System

Consider a continuous time single input—single output second order plant (a process) given in the following canonical state space realization form:

$$ \begin{aligned} \dot{x} & = A_{c} x + B_{c} u \\ y & = C_{c} x \\ \end{aligned}, $$

(15.3)

where

$$ A_{c} = \left[ {\begin{array}{*{20}c} 0 & 1 \\ {a_{1p} } & {a_{2p} } \\ \end{array} } \right],\,B_{c} = \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right],\,C_{c} = \left[ {\begin{array}{*{20}c} {c_{1p} } & {c_{2p} } \\ \end{array} } \right], $$

• u is the control signal,

• y is the output of the plant.

Assume that at the time t parameters $a_{1p}$ and $a_{2p}$ change dramatically due to a fault in the system, but parameters $c_{1p}$ and $c_{2p}$ remain constant. The mathematical model of plant (15.3) can be represented in the following form:

$$ \begin{aligned} \ddot{x}_{p} & = (\bar{a}_{2p} + \Updelta a_{2p} (t))\dot{x}_{p} + (\bar{a}_{1p} + \Updelta a_{1p} (t))x_{p} + u \hfill \\ y_{p} & = \bar{c}_{2p} \dot{x}_{p} + \bar{c}_{1p} x_{p} , \hfill \\ \end{aligned} $$

where

$$ \begin{aligned} a_{1p} = \bar{a}_{1p} + \Updelta a_{1p} (t), \hfill \\ a_{2p} = \bar{a}_{2p} + \Updelta a_{2p} (t), \hfill \\ \end{aligned} $$

• $\bar{a}_{1p} ,\,\bar{a}_{2p} ,\,\bar{c}_{1p} ,\,\bar{c}_{2p}$ are the nominal parameters (constant) of the plant,

• $\Updelta a_{1p} (t),$ $\Updelta a_{2p} (t)$ are the biases of the plant parameters (variable) from their nominal values,

• $x_{p}$ is the plant state,

• $y_{p}$ is the plant output.

A desirable behavior of the plant can be determined by the following reference model:

$$ \begin{aligned} \ddot{x}_{m} & = a_{2 m} \dot{x}_{m} + a_{1 m} x_{m} + g \hfill \\ y_{m} & = c_{2 m} \dot{x}_{m} + c_{1 m} x_{m} \hfill \\ \end{aligned}, $$

(15.4)

where

• g is the input signal,

• $a_{1 m} ,\,a_{2 m} ,\,c_{1 m} ,\,c_{2 m}$ are parameters of the model.

In order to compensate for the plant parameters’ biases, a controller can be used. The closed loop system with the controller is represented in the following form:

$$ \begin{aligned} \ddot{x}_{p} = & (\bar{a}_{2p} + \Updelta a_{2p} (t))\dot{x}_{p} + (\bar{a}_{1p} + \Updelta a_{1p} (t))x_{p} \\ &\,+ (\bar{k}_{2} + \Updelta k_{2} (t))\dot{x}_{p} + (\bar{k}_{1} + \Updelta k_{1} (t))x_{p} + g, \\ \end{aligned} $$

(15.5)

where

• $\bar{k}_{1} ,\,\bar{k}_{2}$ are the constant parameters of the controller,

• $\Updelta k_{1} (t),\,\Updelta k_{2} (t)$ are the adjustable parameters of the controller.

The desirable quality of the process behavior can be obtained from the following relationships:

$$ \begin{aligned} \bar{k}_{1} + \bar{a}_{1p} & = a_{1m} \\ \bar{k}_{2} + \bar{a}_{2p} & = a_{2m}. \\ \end{aligned} $$

According to Eqs. (15.4) and (15.5), the error equation is obtained as follows:

$$ \ddot{e} = a_{2 m} \dot{e} + a_{1 m} e + z_{2} \dot{x}_{p} + z_{1} x_{p} , $$

(15.6)

where

$$ \begin{aligned} e & = x_{m} - x_{p} , \hfill \\ z_{1} & = \Updelta a_{1p} (t) + \Updelta k_{1} (t), \hfill \\ z_{2} & = \Updelta a_{2p} (t) + \Updelta k_{2} (t). \hfill \\ \end{aligned} $$

It can be seen from Eq. (15.6) that in order to achieve the desirable error e → 0, it is necessary to provide the following conditions:

$$ z_{1} \equiv 0,\,z_{2} \equiv 0. $$

(15.7)

The conditions (15.7) can be achieved by adjusting parameters $\Updelta k_{1} (t)$ and $\Updelta k_{2} (t)$ according to the following laws [5]:

$$ \begin{aligned} \Updelta \dot{k}_{1} (t) = \sigma x_{p} \hfill \\ \Updelta \dot{k}_{2} (t) = \sigma \dot{x}_{p} , \hfill \\ \end{aligned} $$

(15.8)

where $\sigma = Pe$.

The positive definite symmetric matrix P can be obtained from the solution of the relevant Lyapunov equation. The main problem associated with algorithms (15.8) is that all self-tuning contours are linked through the dynamics of the plant. The consequence is that high interaction of each contour with others will occur. This further results in poor dynamic compensation of plant parameters’ biases $\Updelta a_{ip}$ (i = 1, 2,…m), where m is a number of self-tuning contours. The idea of decoupling self-tuning contours from plant dynamics, based on simultaneous identification and adaptation, is suggested for the solution of this problem with fault tolerance. This could considerably improve performance of the overall system, especially for high dimension and multivariable plants and processes.

It can be shown [6, 7] that the self-tuning contours will be decoupled from the plant dynamics if σ can be formed such that:

$$ \sigma^{*} = \ddot{e} - a_{2 m} \dot{e} - a_{1 m} e. $$

In this case the following relationship can be obtained:

$$ \sigma^{*} = (\Updelta a_{2p} (t) + \Updelta k_{2} (t))\dot{x}_{p} + (\Updelta a_{1p} (t) + \Updelta k_{1} (t))x_{p} . $$

(15.9)

In order to solve Eq. (15.9) with two variable parameters, the following approach is suggested: Multiply both parts of Eq. (15.9) by state variables $x_{p}$ and $\dot{x}_{p}$ and integrate the resultant equations on the time interval (t ₁ , t ₂), where: t ₂ = t ₁ + Δt. Taking the initial conditions as t ₁ = 0, Δk _i  = 0, (i = 1, 2) the following equations are obtained:

$$ \begin{aligned} \int\limits_{{t_{1} }}^{{t_{1} + \Updelta t}} {\sigma^{*} } x_{p} dt & = \Updelta a_{2p} \int\limits_{{t_{1} }}^{{t_{1} + \Updelta t}} {\dot{x}_{p} x_{p} dt} + \Updelta a_{1p} \int\limits_{{t_{1} }}^{{t_{1} + \Updelta t}} {x_{p}^{2} dt} \\ \int\limits_{{t_{1} }}^{{t_{1} + \Updelta t}} {\sigma^{*} } \dot{x}_{p} dt & = \Updelta a_{2p} \int\limits_{{t_{1} }}^{{t_{1} + \Updelta t}} {\dot{x}_{p}^{2} dt} + \Updelta a_{1p} \int\limits_{{t_{1} }}^{{t_{1} + \Updelta t}} {x_{p} \dot{x}_{p} dt} . \\ \end{aligned} $$

(15.10)

Introduce the following notations:

$$ \begin{aligned} \int\limits_{{t_{1} }}^{{t_{1} + \Updelta t}} {\sigma^{*} } x_{p} dt & = c_{1} ,\,\int\limits_{{t_{1} }}^{{t_{1} + \Updelta t}} {\sigma^{*} } \dot{x}_{p} dt = c_{2} , \\ \int\limits_{{t_{1} }}^{{t_{1} + \Updelta t}} {x_{p}^{2} } dt & = l_{11} ,\,\int\limits_{{t_{1} }}^{{t_{1} + \Updelta t}} {x_{p} \dot{x}_{p} } dt = l_{21} , \\ \int\limits_{{t_{1} }}^{{t_{1} + \Updelta t}} {\dot{x}_{p} } x_{p} dt & = l_{12} ,\,\int\limits_{{t_{1} }}^{{t_{1} + \Updelta t}} {\dot{x}_{p}^{2} } dt = l_{22} . \\ \end{aligned} $$

(15.11)

According to notations (15.11), Eq. (15.10) can now be written in the form:

$$ \begin{aligned} c_{1} & = \Updelta a_{1p} l_{11} + \Updelta a_{2p} l_{12} \\ c_{2} & = \Updelta a_{1p} l_{21} + \Updelta a_{2p} l_{22} . \\ \end{aligned} $$

(15.12)

From the solution of Eq. (15.12) the bias of the plant parameters $\Updelta a_{ip} ,$ (i = 1, 2) can be determined. The controller can be adjusted according to the estimated parameter bias as:

$$ \Updelta k_{i} = - \Updelta a_{ip}. $$

Therefore, conditions (15.7) are satisfied, which in turn means that the behavior of system (15.5) follows the desirable trajectories of model (15.4), even in the presence of dramatic plant parameters changes.

For the solution of Eq. (15.12) one needs to take into account of the hypothesis of quasi-stationarity of the process, where the interval time Δt is selected such that the biases of parameters $\Updelta a_{ip}$ must be constant at this interval. However, the interval Δt should be sufficiently large in order to accumulate a larger quantity of variables $x_{p}$ and $\dot{x}_{p}$ for the solution of the equations.

15.3 The Numerical Results

The Hankel matrix Γ, constructed from the Markov parameters (obtained from the experiment, see Appendix), is as follows:

$$ \Upgamma = \left[ {\begin{array}{*{20}c} {6.5000000 \text{e} - 02} & {1.4550000 \text{e} - 01} & {1.6442500 \text{e} - 01} \\ {1.4550000 \text{e} - 01} & {1.6442500 \text{e} - 01} & {1.5056000 \text{e} - 01 \, } \\ {1.6442500 \text{e} - 01} & {1.5056000 \text{e} - 01} & {1.2447038 \text{e} - 01} \\ \end{array} } \right]. $$

(15.13)

Applying the singular value decomposition procedure (15.1) on the Hankel matrix (15.13), it is found that

$$ U = \left[ {\begin{array}{*{20}c} {5.1633320 \text{e} - 01} & {8.1190203 \text{e} - 01} & {2.7242453 \text{e} - 01} \\ {6.2194166 \text{e} - 01} & { - 1.3682059 \text{e} - 01 \, } & { - 7.7101797 \text{e} - 01} \\ {5.8871776 \text{e} - 01} & { - 5.6753434 \text{e} - 01} & {5.7560070 \text{e} - 01} \\ \end{array} } \right] $$

$$ V = \left[ {\begin{array}{*{20}c} {5.1633320 \text{e} - 01} & { - 8.1190203 \text{e} - 01} & {2.7242453 \text{e} - 01} \\ {6.2194166 \text{e} - 01} & {1.3682059 \text{e} - 01} & { - 7.7101797 \text{e} - 01} \\ {5.8871776 \text{e} - 01} & {5.6753434 \text{e} - 01} & {5.7560070 \text{e} - 01} \\ \end{array} } \right] $$

$$ S = \left[ {\begin{array}{*{20}c} {4.2773559 \text{e} - 01} & {0.0000000 \text{e} + 00} & {0.0000000 \text{e} + 00} \\ {0.0000000 \text{e} + 00} & {7.4455532 \text{e} - 02} & {0.0000000 \text{e} + 00} \\ {0.0000000 \text{e} + 00} & {0.0000000 \text{e} + 00} & {6.1531296 \text{e} - 04} \\ \end{array} } \right]. $$

(15.14)

Using relations (15.1), (15.2) and (15.14) the discrete time state space realization of the reduced order system is obtained as follows:

$$ A_{d} = \left[ {\begin{array}{*{20}c} {9.7950468 \text{e} - 01} & { - 3.4211654 \text{e} - 01} \\ {3.4211654 \text{e} - 01} & {3.4867831 \text{e} - 01} \\ \end{array} } \right] $$

$$ \begin{aligned} B_{d} & = \left[ {\begin{array}{*{20}c} {3.3767560 \text{e} - 01} \\ { - 2.2160613 \text{e} - 01} \\ \end{array} } \right] \hfill \\ C_{d} & = \left[ {3.3767560 \text{e} - 01\quad 2.2160613 \text{e} - 01} \right] \hfill \\ \end{aligned} $$

(15.15)

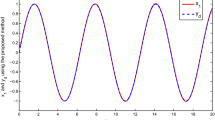
The behavior of the full order model and the reduced order model is given in Fig. 15.1. It can be seen in Fig. 15.1 and Appendix that the Markov parameters of the reduced order model are a close approximation to the Markov parameters of the original system.

Fig. 15.1

The behavior of the full order model and reduced order model

Nominal parameters of the plant in the continuous time (15.3) are obtained from (15.15) as follows:

$$ \begin{aligned} \bar{a}_{1p} & = - 3.1184,\,\bar{a}_{2p} = - 3.0517, \\ \bar{c}_{1p} & = - 0.0318,\,\bar{c}_{2p} = 2.9132. \\ \end{aligned} $$

Parameters of model (15.4) are chosen as $a_{1 m} = \bar{a}_{1p}$, $a_{2 m} = \bar{a}_{2p}$, $c_{1 m} = \bar{c}_{1p}$, $c_{2 m} = \bar{c}_{2p}$.

The performance of the high dynamic precision adaptive control system is presented in Figs. 15.2, 15.3, 15.4, 15.5.

Fig. 15.2

Bias Δa_1p = 1, Δa_2p = 0. The adaptation is switched off

Fig. 15.3

Bias Δa_1p = 1, Δa_2p = 0. The adaptation is switched on

Fig. 15.4

Bias Δa_1p = 0, Δa_2p = 1. The adaptation is switched off

Fig. 15.5

Bias Δa_1p = 0, Δa_2p = 1. The adaptation is switched on

Figure 15.2 shows that the bias from the nominal parameter at time $t \ge 1\;\text{s}$ is $\Updelta a_{1p} = 1,$ ($\Updelta a_{2p} = 0$). The adaptation is switched off.

Figure 15.3 shows the bias from the nominal parameter at $t \ge 1\;\text{s}$ with adaptation being switched on ($\Updelta a_{1p} = 1,$ $\Updelta a_{2p} = 0$). It can be seen that the output of system $y_{p}$ coincides with the model reference output $y_{m}$ after $t \ge 4\;\text{s} .$

Figure 15.4 shows that the bias from the nominal parameter at time $t \ge 1\;\text{s}$ is $\Updelta a_{2p} = 1,$ ($\Updelta a_{1p} = 0$). The adaptation is switched off.

Figure 15.5 shows the bias from the nominal parameter at $t \ge 1\;\text{s}$ with adaptation being switched on ($\Updelta a_{2p} = 1$, $\Updelta a_{1p} = 0$). It can be seen that the output of system $y_{p}$ coincides with the model reference output $y_{m}$ after $t\geq9\;\text{s}$.

15.4 Conclusions

The high dynamic precision adaptive control system for the solution of a fault tolerance problem of a single–input–single–output process is suggested in this paper. The method, which is based on simultaneous identification and adaptation of unknown process parameters, provides decoupling of self-tuning contours from plant dynamics. The control system compensates the rapidly changing parameter when fault occurs in a process. The mathematical model of the process is formed from Markov parameters, which are obtained from the experiment as the process impulse response. The order of the model is determined using singular value decomposition of the relevant Hankel matrix. This allows one to obtain a robust reduced order model representation if the information about the process is corrupted by noise in industrial environment. The adaptive control can be used for the solution of a fault tolerance problem [8] in complex and multivariable processes and systems.

Appendix

Markov parameters obtained from the experiment	Markov parameters of the reduced order model
0.0000000e + 00	0.0000000e + 00
6.5000000e − 02	6.4934730e − 02
1.4550000e − 01	1.4578163e − 01
1.6442500e − 01	1.6384913e − 01
1.5056000e − 01	1.5077128e − 01
1.2447038e − 01	1.2511681e − 01
9.7003263e − 02	9.7037520e − 02
7.2809279e − 02	7.1509116e − 02
5.3273657e − 02	5.0478548e − 02
2.7143404e − 02	3.4252666e − 02
1.9054881e − 02	2.2345734e − 02
1.3274250e − 02	1.3971877e − 02
9.1920232e − 03	8.3100499e − 03
6.3351771e − 03	4.6301281e − 03
4.3498142e − 03	2.3388797e − 03
2.9776238e − 03	9.8319708e − 04
2.0333343e − 03	2.3330942e − 04
1.3857582e − 03	−1.4099694e − 04
9.4289895e − 04	−2.9426412e − 04
6.4072233e − 04	−3.2618265e − 04