Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

10.1 Introduction

Since the discovery of quasicrystals, much research has been directed at their unique structure and physical properties, especially quasiperiodicity [1, 2]. Ordering and excitations of quasiperiodically arranged magnetic moments (spins) remain fundamental open problems, despite the intensive efforts continuously made since the discovery of quasicrystals. The Zn–Mg–R (R = rare-earth) icosahedral quasicrystals [3] are the most extensively studied magnetic quasicrystals because of the following experimental advantages. These quasicrystals have well-localized, mostly isotropic and sizable 4f magnetic moments. Their atomic structure is relatively well known. Sato et al. [4] have investigated the low-temperature spin dynamics in the face-centered-icosahedral Zn–Mg–Tb quasicrystal around its spin-glass-like freezing temperature by inelastic neutron scattering. They observed the broad inelastic peak, which can be interpreted as localized collective fluctuations of short-range-ordered spins in a dodecahedral spin cluster. Furthermore, they gave a very important suggestion. That is, they indicated a possible close relation between the broad inelastic spin-excitation peak and the so-called boson peak in topological glasses [5, 6]. The boson peak is a broad inelastic excitation peak universally observed in vibrational spectra of topological glasses at a Q-independent excitation energy of a few meV. Its intensity shows a Q-dependence similar to the static structure factor, whereas its temperature dependence is given by the Bose temperature factor. The boson peak is given by the Bose temperature factor. The boson peak is believed to be related to collective atomic vibrations in a small structural unit. These characteristics are surprisingly similar to those of the observed inelastic spin-excitation peak, and thus, at least phenomenologically, we may regard the inelastic peak as a spin analogue of the boson peak.

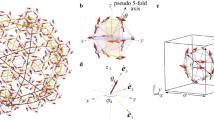
One of the present authors (I.K.) [7–11] has introduced a generalized view of the physical origin of the boson peak in the gauge-invariant formula. Especially the localized modes (massive gauge modes), which correspond to the boson peak, are required naturally through the Higgs mechanism. In this study, we shall propose the mechanism of localized collective fluctuations of short-range-ordered spin in a dodecahedral spin cluster (Fig. 10.1) and discuss the relation to the boson peak in topological glasses, by using the theoretical formula [8–11].

Fig. 10.1
figure 1

Dodecahedral spin cluster model. A typical ground-state spin configuration is shown by the thick solid lines. The nearest-neighbor (J 1) and next nearest-neighbor (J 2) interactions are also indicated by arrows

Full size image

10.2 Localized Collective Spin-Fluctuation and the Boson Peak

It has been proposed that the parameter ϕ a (t,r,u) (a=1–4), whose t, r, and u are the time axis, the spatial axes and the perpendicular axes, in the quasicrystal is specified by the rotation, which is related to the gauge fields SO(4) of \(A_{\mu }^{a}\) [11, 12], where a=1–4 and μ=1,2,3 correspond to the physical space axes, and μ=4,5,6 correspond to the perpendicular space axes. To represent the dodecahedral cluster, we set the symmetry breaking 〈0|ϕ a |0〉=〈0,0,0,ν〉 of the Bose parameter field ϕ a in the Lagrange density as follows:

(10.1)

After the symmetry breaking 〈0|ϕ a |0〉=〈0,0,0,ν〉, we can obtain the effective Lagrange density as follows:

(10.2)

where S j is the spin of Tb and m 1=ν⋅g 4, \(m_{2} = 2( 2 )^{\frac{1}{2}}\lambda\cdot\nu\). The effective Lagrange density describes three massive gauge fields. \(A_{\mu }^{1} \), \(A_{\mu }^{2}\) and \(A_{\mu }^{3}\) are created through the Anderson–Higgs mechanism by introducing the dodecahedral cluster, the fields \(A_{\mu }^{1}\), \(A_{\mu }^{2}\), and \(A_{\mu }^{3}\) are then localized around the dodecahedral cluster within the length of ∼1/|m 1|=(ν.g 4)−1≡R c .R c approximately corresponds to the radius of the dodecahedral cluster.

From the first term in Eq. (10.2), it is shown that the massive gauge fields \(A_{\mu }^{1}\), \(A_{\mu }^{2}\), and \(A_{\mu }^{3}\) induce localized collective fluctuation of spins in a dodecahedral spin cluster, taking into account the short-range spin fluctuation mechanism by massive gauge fields [15].

Now we shall consider the relation to the so-called boson peak in topological glasses. It is preferable that we think of the anomalous density fluctuations in three-dimensional liquids (glasses) as the hedgehog-like clusters, taking account of the curvature, as shown intuitively in Fig. 10.2.

Fig. 10.2
figure 2

Hedgehog-like fluctuation (cluster), which is similar to the three-dimensional sphere S 3, with the approximate radius of the inverse of mass, m 1, introduced by the Higgs mechanism

Full size image

We adopt the parameter ρ(r,u)≡ρ a(a=1,2,3,4), which is similar to that in the Sachdev and Nelson model [12]. The SO(4) quadruplet fields \(A_{\mu }^{a}\) are spontaneously broken through the fluid host around the hedgehog-like fluctuation (cluster) [13, 14]. When the hedgehog-like cluster (soliton) is created, we set the symmetry breaking of the quadruplet fields, 0|ρ|0〉, equal to 〈0,0,0,ν 4〉.

Now we approximately introduce the Lagrange density as follows:

(10.3)

Then we set the symmetry breaking as follows:

$$\rho^{a} \to( 0,0,0,\nu_{4} ) + \bigl( \rho^{1}, \rho^{2},\rho^{3},\rho^{4} \bigr). $$

Thus we can introduce the effective Lagrange density

(10.4)

Here m 1 is ν 4⋅g and m 2 is \(2\sqrt{2\lambda \cdot \nu_{4}}\).

The effective Lagrange density, L eff, represents three massive vector fields \(A_{\mu }^{1}\), \(A_{\mu }^{2}\), and \(A_{\mu }^{3}\), and the masses are created through the Higgs mechanism by introducing the hedgehog-like clusters (solitons), the gauge fields \(A_{\mu }^{1},A_{\mu }^{2}\), and \(A_{\mu }^{3}\) are only present around clusters. The inverse, 1/|m|, of the mass of \(A_{\mu }^{1}\), \(A_{\mu }^{2}\), and \(A_{\mu }^{3}\) reveals approximately the radius of the clusters.

Since the gauge field \(A_{\mu }^{4}\) is massless, it is thought that the gauge field \(A_{\mu }^{4}\) mediates the long-range interaction between two excited clusters (the hedgehog-like solitons).

In glasses and amorphous materials, the broad maximum of Raman spectra and neutron scattering is due to excess vibrational density of states. It is the so-called boson peak because its intensity changes with T in accordance with the Bose–Einstein factor. It is thought that the vibrational states responsible for the boson peak contribute also to the thermal conductivity plateau because the energy range spanned by the plateau covers that of the boson peak spectra, indicating that acoustic excitations must cease to propagate when their wavelength λ reaches the nm range. That is, acoustic modes may become strongly localized modes, satisfying the Ioffe–Regel condition. By a computer simulation of a soft sphere glass, it is found that there are (quasi)localized modes with effective masses ranging from 10 atomic masses upwards, which are related to the boson peak. In the present theoretical formulation, the effective Lagrangian represents three massive vector fields \(A_{\mu }^{1}\), \(A_{\mu }^{2}\), and \(A_{\mu }^{3}\) which are localized within a radius, 1/|m|, around the hedgehog-like clusters [13]. Thus, it is suggested that the localized gauge fields \(A_{\mu }^{1}\), \(A_{\mu }^{2}\), and \(A_{\mu }^{3}\) around the hedgehog-like clusters (solitions) are related to the (quasi)localized modes of the boson peak. Expanding the present formula, we can introduce a more generalized view of the origin of the boson peak. We adopt the generalized parameter,

$$\rho( r,u ) \equiv\rho^{a}\quad ( a = 1,2,3,4,5,\ldots,N ). $$

When the locally favored cluster is created, we set the symmetry breaking of 0|ρ b|0=0, in which b represents components within the components from a=m to N. As a result, m−1 massive gauge modes (the localized modes) are introduced around the locally favored cluster through the Higgs mechanism.

It should be noticed that the massive gauge fields \(A_{\mu }^{1}\), \(A_{\mu }^{2}\), and \(A_{\mu }^{3}\) in Eq. (10.2) are certainly similar to the ones in Eq. (10.4). Thus, the massive gauge fields \(A_{\mu }^{1}\), \(A_{\mu }^{2}\), and \(A_{\mu }^{3}\), which correspond to the boson peak, induce localized collective fluctuations of spins in a dodecahedral spin cluster. This suggests that we may regard the inelastic peak as a spin analogy of the boson peak.

10.3 Conclusion

We have proposed the mechanism of localized collective spin-fluctuation in a dodecahedral spin cluster. Massive gauge fields, which correspond to the boson peak, induce localized collective spin-fluctuation in a dodecahedral spin clusters.