Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

The roots of hydrostatic fundamentals for solution of the problems in dynamics of celestial bodies date back to the distant past and are related to the founders of modern science. But even at that time, these pioneers understood well that the applicability of the hydrostatic equilibrium to a body’s dynamic problems is restricted by certain boundary conditions. Thus, Newton in his Principia (Sect. 1.5 of Book III), while considering the conditions of attraction in the planets, writes: “The attraction being spread from the surface downwards is approximately proportional to distance of the center. Be the planet’s matter uniform in density, then this proportion would have exact value. It follows from here that the error is caused by non-uniformity in density.” At that time, the thoughts of scientists were engaged with how to solve the principle problem of a body’s orbital motion. Now, we search its correct solution.

Recall briefly the conditions of a body in hydrostatic equilibrium. By definition, hydrostatics is a branch of hydromechanics which studies the equilibrium of a liquid and gas and the effects of a stationary liquid on immersed bodies relative to the chosen reference system. For a liquid equilibrated relative to a rigid body, when its velocity of motion is equal to zero and the field of densities is steady, the equation of state follows from the Eulerian and Navier–Stokes equations in the form (Landau and Lifshitz 1954; Sedov 1970)

$$ \mathrm{grad}\,p=\rho F, $$
(2.1)

where р is the pressure, ρ is the density, and F is the mass force.

In the Cartesian system of reference, Eq. (2.1) is written as

$$ \begin{gathered} \frac{{\partial p}}{{\partial x}}=\rho {F_x}, \hfill \\ \frac{{\partial p}}{{\partial y}}=\rho {F_y}, \hfill \\ \frac{{\partial p}}{{\partial z}}=\rho {F_z}.\end{gathered} $$
(2.2)

If the outer mass forces are absent, that is, F x  = F y  = F z  = 0, then

$$ \mathrm{grad}\,p=0. $$

In this case, in accordance with Pascal’s law, the pressure in all liquid points will be the same.

For the uniform incompressible liquid, when ρ = const, its equilibrium can be only in the potential field of the outer forces. For the general case of an incompressible liquid and the potential field of the outer forces from (2.1), one has

$$ \mathrm{d}p=\rho\,\mathrm{d}U, $$
(2.3)

where U is the forces’ potential.

It follows from Eq. (2.3) that for the equilibrated liquid in the potential force field, its density and pressure appear to be a function only of the potential U.

For a gravity force field, when in the steady-state liquid only these forces act, one has

$$ {F_x}={F_y}=0,\quad {F_z}=-g, \quad U=-gz+\mathrm{const}\quad \mathrm{and}\quad p=p(z),\quad \rho =\rho (z). $$

Here, the surfaces of the constant pressure and density appear as the horizontal planes. Then Eq. (2.3) is written in the form

$$ \frac{{\mathrm{d}p}}{{\mathrm{d}z}}=-\rho g<0. $$
(2.4)

It means that with elevation, the pressure falls, and with depth, grows. From here it follows that

$$ p-{p_0}=-\int\limits_{{{z_0}}}^z {\rho g\,\mathrm{d}z=-\rho g\left( {z-{z_0}} \right)}, $$
(2.5)

where g is the acceleration of the gravity force.

If a spherical vessel is filled by an incompressible liquid and rotates around its vertical axis with constant angular velocity ω, then for determination of the equilibrated free surface of the liquid in Eq. (2.2), the centrifugal inertial forces should be introduced in the form

$$ \begin{gathered} \frac{{\partial p}}{{\partial x}}=\rho {\omega^2}x, \hfill \\ \frac{{\partial p}}{{\partial x}}=\rho {\omega^2}y, \hfill \\ \frac{{\partial p}}{{\partial x}}=-\rho g.\end{gathered} $$
(2.6)

From here, for the rotating body with radius r 2 = x 2 + y2, one finds

$$ p=-\rho gz+\frac{{\rho {\omega^2}{r^2}}}{2}+C. $$
(2.7)

For the points on the free surface r = 0, z = z 0, one has р = р 0. Then,

$$ C={p_0}+\rho g{z_0}, $$
(2.8)
$$ p={p_0}+\rho g\left( {{z_0}-z} \right)+\frac{{\rho \omega {r^2}}}{2}. $$
(2.9)

The equation of the liquid free surface, where р = р 0, has a paraboloidal shape

$$ z-{z_0}=\frac{{{\omega^2}{r^2}}}{2g }. $$
(2.10)

These facts determine the principal physical conditions and equations of the hydrostatic equilibrium of a liquid. They remain a basis of the modern dynamics and theory of the planet’s figure. Attempts to harmonize these conditions with the planet’s motion conditions have failed, as proven by observation. The main obstacle for such harmonization is the condition (2.1), which ignores the planet’s inner force field and without which the hydrostatics is unable to provide the equilibrium between the body interacted forces as Newton’s third law requires. The Earth and other planets are self-gravitating bodies. Their matter moves in their own force field which is generated by the mass particle interaction. The mass density distribution, rotation, and oscillation of the body shells result from the inner force field. And the orbital motion of the planets is controlled by interaction of the outer force fields of the planets and the Sun in accordance with Newton’s theory.

Because any celestial body is de facto self-gravitating systems, we will study equilibrium in its own force field of the interacted masses. It is shown that by action of this field, separation of the masses in density, oscillation, and axial rotation results. In this case, the planet’s orbital motion will originate by the Sun’s first cosmic velocity of the outer protosun’s surface force field. But first, the proposed models of the hydrostatic equilibrium are discussed.

2.1 Newton’s Model of Hydrostatic Equilibrium of a Uniform Body

In Section V of Book II Density and Compression of Fluids: Hydrostatics, Newton formulates the hydrostatic laws, and on their basis in Book III The System of the World, he considers the problem of the Earth’s oblateness by applying real values of the measured distances between Landon and York, Amiens and Malvoisine, Collioure and the observatory of Paris, and the Observatory and the Citadelo of Dunkirk.

Taking advantage of measurements, Newton calculated the ratio of the total gravitation force over the Paris latitude to the centrifugal force over the equator and found that the ratio is equal to 289:1. After that, he imagines the Earth in the form of an ellipse of rotation (Fig. 2.1) with axis PQ and channel ACQqca.

Fig. 2.1
figure 1

Newton’s problem of the Earth’s oblateness

Full size image

If the channel is filled in with water, then its weight in the branch АСса will be related to the water weight in the branch QСсq as 289:288 because of the centrifugal force which decreases the water weight in the last branch by the unit. He found by calculation that if the Earth has a uniform mass of matter and has no any motion and the ratio of its axis PQ to the diameter АВ is 100:101, then the gravity force of the Earth at the point Q relates to the gravity force at the same point of the sphere with radius СQ or СР as 126:125. By the same argument, the gravity in point А of a spheroid drawn by revolution around axis АВ relates to the gravity in the same point of the sphere drown from center С with radius АС as 125:126. However, since there is one more perpendicular diameter, then this relation should be 126:1251/2. Having multiplied these ratios, Newton found that the gravity force at point Q relates to the gravity force at point А as 501:500. Because of daily rotation, the liquid in the branches should be in equilibrium at a ratio of 505:501. So, the centrifugal force should be equal to 4/505 of the weight. In reality, the centrifugal force composes 1/289. Thus, the excess in water height under the action of the centrifugal force in the branch Асса is equal to 1/289 of the height in branch QСсq.

After calculation by hydrostatic equilibrium in the channels, Newton obtained that the ratio of the Earth’s equatorial diameter to the polar diameter is 230:229, that is, its oblateness is equal to (230−229)/230 = 1/230. This result demonstrating that the Earth’s equatorial area is higher than the polar region was used by Newton for explanation of the observed slower swinging of pendulum clocks on the equator than on the higher latitudes.

Thus, applying the found measurements and the hydrostatic approach, he calculated the Earth’s oblateness equal to 1/230, where in his consideration the centrifugal force plays the main contraction effect expanding the body along the equator. In fact, the task is related to the creation of an ellipsoid of rotation from a sphere by action of the centrifugal force. Here, Newton applied his idea that the attraction of the planet itself goes from the surface to its center. In this case, the total sum of the centripetal forces and the moments is equal to zero, and rotation of the Earth should be inertial. It means that the planet’s angular velocity has a constant value.

Inertial rotation of the Earth is accepted a priori. There is no evidence or other form of justification for this phenomenon. There are also no ideas relative to the mode of the planet’s rotation, namely, whether it rotates as a rigid body or there is differential rotation of separate shells. In modern courses of mechanics, there is only analytical proof that in case the body occurs in the outer field of central forces, then the sum of its inner forces and torques is equal to zero. Thus, it follows that the Earth’s rotation should have a mode of rigid body, and the velocity of rotation in time should be constant.

The proof of the conclusion that if a body occurs in the field of the central forces, then the sum of the inner forces and torques is equal to zero, and the moment of momentum has a constant value, is directly related to the Earth’s dynamics. Let us see it in modern presentation (Kittel et al. 1965).

Write the expression of the moment of momentum L for a mass point m, the location of which is determined by radius vector r relative to an arbitrarily selected fixed point in an inertial system of coordinates

$$ \mathbf{L}\equiv \mathbf{r}\times \mathbf{p}\equiv \mathbf{r}\times m\mathbf{v}, $$
(2.11)

where р is the moment and v is the velocity.

The torque N relative to this point is equal to

$$ \mathbf{N}\equiv \mathbf{r}\times \mathbf{F}, $$

where F is the force acting on a particle.

After differentiation of (2.11) with respect to time, one obtains

$$ \frac{{\mathrm{d}\mathbf{L}}}{{\mathrm{d}t}}=\frac{\mathrm{d}}{{\mathrm{d}t}}\left( {\mathbf{r}\times \mathbf{p}} \right)=\frac{{\mathrm{d}r}}{{\mathrm{d}t}} \times \mathbf{p}+\mathbf{r}\times \frac{{\mathrm{d}\mathbf{p}}}{{\mathrm{d}t}}. $$
(2.12)

Since vectorial product

$$ \frac{{\mathrm{d}r}}{{\mathrm{d}t}} \mathbf{r}\times \mathbf{p}=\mathbf{v}\times m\mathbf{v}=0, $$
(2.13)

then taking into account the second Newton’s law for the inertial reference system, we have

$$ \mathbf{r}\times \frac{{\mathrm{d}\mathbf{p}}}{{\mathrm{d}t}}=\mathbf{r}\times \mathbf{F}=\mathbf{N}, $$

from where

$$ \mathbf{N}=\frac{{\mathrm{d}\mathbf{L}}}{{\mathrm{d}t}}. $$
(2.14)

For the central force \( \mathbf{F}={\hat{\mathbf{r}}} f(r) \), which acts on the mass point located in the central force field, the torque is equal to

$$ \mathbf{N}=\mathbf{r}\times \mathbf{F}=\mathbf{r}\cdot \hat{\mathbf{r}} f(r)=0. $$
(2.15)

Consequently, for the central forces, the torque is equal to zero, and the moment of momentum L appears to be constant.

In the case where the mass point presents a body composed of n material particles, then the moment of momentum L of that system will depend on location of the origin of the reference system. If the reduced vector of the mass center of the system relative to the origin is R c, then the equation for the moment of momentum L is written as

$$ \mathbf{L}=\sum\limits_{n=1}^N {{m_n}({{\mathbf{r}}_n}-{{\mathbf{R}}_{\mathrm{c}}}) \times {{\mathbf{v}}_n}} +\sum\limits_{n=1}^N {{m_n}{{\mathbf{R}}_{\mathrm{c}}}} \times \mathbf{v}={{\mathbf{L}}_{\mathrm{c}}}+\mathbf{R}{}_{\mathrm{c}} \times \mathbf{P}, $$
(2.16)

where L c is the moment of momentum relative to the system’s center of the masses; \( \mathbf{P}=\sum {{m_n}} \times {{\mathbf{v}}_n} \) is the total moment of the system. Here, the term R c × P expresses the moment of momentum of the mass center and depends on the origin, and the term L c, on the contrary, does not depend on the reference system.

$$ \mathbf{N}=\sum\limits_{n=1}^N {{{\mathbf{r}}_n}} \times {{\mathbf{F}}_n}, $$

and the sum of the inner forces is

$$ {{\mathbf{F}}_i}=\sum\limits_{n=1}^N {{{\mathbf{F}}_{ij }}}; $$
(2.17)

here and further, the summing is done at condition i ≠ j.

The torque of the inner forces is

$$ {{\mathbf{N}}_{\mathrm{in}}}=\sum\limits_i {{{\mathbf{r}}_i}} \times {{\mathbf{F}}_i}=\sum\limits_i {\sum\limits_j {{{\mathbf{r}}_i}} } \times {{\mathbf{F}}_{ij }}. $$
(2.18)

Since

$$ \sum\limits_i {\sum\limits_j {{{\mathbf{r}}_i}} } \times {{\mathbf{F}}_{ij }}=\sum\limits_i {\sum\limits_j {{{\mathbf{r}}_j}} } \times {{\mathbf{F}}_{ji }}, $$
(2.19)

then the torque of inner forces can be presented in the form

$$ {{\mathbf{N}}_{\mathrm{in}}}=\frac{1}{2}\sum\limits_i {\sum\limits_j {\left( {{{\mathbf{r}}_i}\times {{\mathbf{F}}_{ij }}+{{\mathbf{r}}_j}\times {{\mathbf{F}}_{ji }}} \right)} } . $$
(2.20)

Because Newton’s forces F ji  = −F ij , then

$$ {{\mathbf{N}}_{\mathrm{in}}}=\frac{1}{2}\sum\limits_i {\sum\limits_j {\left( {{{\mathbf{r}}_i}-{{\mathbf{r}}_j}} \right)} } \times {{\mathbf{F}}_{ij }}. $$
(2.21)

Taking into account that central forces F ij are parallel to r i  − r j ,

$$ \left( {{{\mathbf{r}}_i}-{{\mathbf{r}}_j}} \right)\times {{\mathbf{F}}_{ij }}=0, $$

from where the torque of the inner forces is equal to zero.

$$ {{\mathbf{N}}_{\mathrm{in}}}=0. $$
(2.22)

Assuming that the inner forces F in = 0, then from (2.15), (2.16), and (2.22) one finds that

$$ \frac{\mathrm{d}}{{\mathrm{d}t}}{{\mathbf{L}}_{\sum }}={{\mathbf{N}}_{\mathrm{ex}}} $$
(2.23)
$$ {{\mathbf{L}}_{\sum }}={{\mathbf{L}}_{\mathrm{c}}}+{{\mathbf{R}}_{\mathrm{c}}}\times \mathbf{P}. $$
(2.24)

Here, L c is also the moment of momentum relative to the mass center, and R × P is the moment of momentum of the mass center relative to an arbitrarily taken origin.

For practice, it is often convenient to select the geometric center of the mass as an origin. In this case, the derivative from the moment of momentum relative to the mass center is the torque of the outer forces, that is,

$$ \frac{\mathrm{d}}{{\mathrm{d}t}}{{\mathbf{L}}_{\mathrm{c}}}={{\mathbf{N}}_{\mathrm{ex}}}. $$
(2.25)

It is seen from the previous classical consideration that in the model of two interacted mass points reduced to the common mass center, which Newton used for solution of Kepler’s problem, resulting in the planets’ motion around the Sun, the inner forces and torques in the central force field are really equal to zero. The torque, which is a derivative with respect to time from the moment of momentum of material particles of the body’s material particles, is determined here by the resultant of the outer forces and the planet’s orbits in the central force field that exists in the same plane. This conclusion follows from Kepler’s laws of the planets’ motion.

Passing to the problem of the Earth’s dynamics, Newton had no choice for the formulation of new conditions. The main conditions were determined already in the two-body problem where the planet appeared in the central force field of the reduced masses. The only difference here is that the mass point has a finite dimension. The condition of zero equality of the inner forces and torques of the rotating planet should mean that the motion could result from the forces among which the known were only the Galilean inertial forces. Such a choice followed from the inertial motion condition of two-body motion which he had applied. The second part of the problem related to reduction of the two bodies to their common center of masses and to the central force that appeared accordingly as predetermining the choice of the equation of state. Being in the outer uniform central force field, it became the hydrostatic equilibrium of the body state. The physical conception and mathematical expression of hydrostatic equilibrium of an object based on Archimedes’ laws (third century BP) and Pascal’s law (1663) were well known in that time. This is the story of the sphere model with the equatorial and polar channels filled in by a uniform liquid mass in the state of hydrostatic equilibrium at inertial rotation.

In Newton’s time, the dynamics of the Earth in its direct sense had not been found as it is absent up to now. The planet, rotating as an inertial body and deprived of its own inner forces and torques, appeared to be a dead–alive creature. But up to now, the hydrostatic equilibrium condition, proposed by Newton, is the only theoretical concept of the planet’s dynamics because it is based on the two-body problem solution which satisfies Kepler’s laws and in practice plays the role of Hooke’s law of elasticity.

In spite of the discrepancies noted here, the problem of determining the Earth’s oblateness was the first step towards the formulation and solution of the very complicated task of determining the planet’s shape, an effort on which theoretical and experimental study continues up to the present time. As to the value of the polar oblateness of the Earth, it appears to be much higher than believed before. More recent observations and measurements show that relative flattening has a smaller value, and Newton’s solution needs to have further development. And its nature disappeared in the heterogeneous mass density of the body.

2.2 Clairaut’s Model of Hydrostatic Equilibrium of a Nonuniform Body

Aleksi Klod Clairaut (1713–1765), a French mathematician and astronomer, continued working on Newton’s solution of the problem of the Earth’s shape based on hydrostatics (Clairaut 1947). The degree measurements in the equatorial and northern regions made in the eighteenth century by French astronomers proved Newton’s conclusion about the Earth’s oblateness, which at that time was regarded with scepticism. But the measured value of the relative flattening appeared to be different. In the equatorial zone, it was equal to 1/314, and in the northern region, to 1/214 (Grushinsky 1976). Clairaut himself took part in the expeditions and found that Newton’s results are not correct. It was also known to him that the Earth is not a uniform body. Because of that, he focused on taking into account the consideration of this effect. Clairaut’s model was represented by an inertia-rotating body filled with liquid of a changing density. In its structure, such a model was closer to the real Earth having a shell structure. But the hydrostatic equilibrium condition and inertial rotation remained to be as previously the physical basis for the problem solution. Clairaut introduced a number of assumptions in the formulation of the problem. In particular, since the velocity of inertial rotation and the value of the oblateness are small, the boundary areas of the shells and their equilibrium were taken as ellipsoidal figures with a common axis of rotation. Clairaut’s solution comprised obtaining a differential equation for the shell-structured ellipsoid of rotation relative to geometric flattening of its main section. Such an equation was found in the form (Melchior 1972)

$$ \frac{{{{\mathrm{d}}^2}e}}{{\mathrm{d}{a^2}}}+\frac{{\mathrm{d}\rho\,{a^2}}}{{\int\limits_0^a {\rho {a^2}\,\mathrm{d}a} }}\frac{{\mathrm{d}e}}{{\mathrm{d}a}}+\left( {\frac{{2\rho a}}{{\int\limits_0^a {\rho {a^2}\,\mathrm{d}a} }}-\frac{6}{{{a^2}}}} \right)e=0, $$
(2.26)

where e = (b−a)/a is the geometric flattening, a and b are the main axes, and ρ is the density.

The difficulty in solving the previous equation was in the absence of the density radial distribution law of the Earth. Later on, by application of seismic data, researchers succeeded in obtaining a picture of the planet’s shell structure. But quantitative interpretation of the seismic observations relative to the density appeared to be possible again, based on the same idea of hydrostatic equilibrium of the body masses. In spite of that, as a result of analysis of the Clairaut’s equation, a number of dynamic criteria for a rotating Earth were obtained. In particular, the relationship between the centrifugal and the gravity force on the equator was found, the ratio between the moments of inertia of the polar and equatorial axes (dynamical oblateness) was obtained, and also the dependence of the gravity force on the latitude of the surface area was derived. That relationship is as follows:

$$ g={g_{\mathrm{a}}}\left( {1-\beta\,\mathrm{si}{{\mathrm{n}}^2}\varphi } \right), $$
(2.27)

where φ is the latitude of the observation point; g e is the acceleration of the gravity force: β = 5/2q−e; q = ω 2 a/g e is the ratio of the centrifugal force to the gravity force on the equator; ω is the angular velocity of the Earth’s rotation; e is the geometric oblateness of the planet; and а is the semimajor axis.

The solutions obtained by Clairaut and further developed by other authors became a theoretical foundation for practical application in the search for the planet’s shape, for interpretation of seismic observation relative to the structure and density distribution of the Earth, and also for analysis of the observed natural dynamic processes.

Later on, the quantitative values of the geometric and dynamic oblateness of the Earth and the Moon, different in values, were obtained by Clairaut’s equation and with the use of satellite data. This fact underlies the conclusion that the Earth and the Moon do not stay in hydrostatic equilibrium.

2.3 Euler’s Model of Hydrostatic Equilibrium of a Rotating Rigid Body

Leonard Euler (1707–1783), a prominent Swiss mathematician, mechanic, and physicist, possessed a great capacity for work, fruitful creativity, and extreme accuracy and strictness in problem solution. There are about 850 titles in the list of his publications, and their collection comprises 72 volumes. Half of them were prepared in Russia. He was twice invited to work in the St. Petersburg Academy of Sciences, where he spent more than 30 years. The spectrum of Euler’s scientific interests was very wide. In addition to mathematics and physics, they included the theory of elasticity, theory of machines, ballistics, optics, shipbuilding, theory of music, and even insurance business. But 3/5 of the work were devoted to mathematics problems.

In mechanics, Euler developed a complete theory of motion of the rigid (nondeformable) body. His dynamic and kinematics equations became the main mathematical instrument in the solution of the rigid body problems. These equations, with the use of the known law of a body rotation, enable the determination of the acting forces and torques. And vice versa, by the applied outer forces, one may find the law of motion (rotation, precession, nutation) of a body.

On the basis of Newton’s equations of motion for rotational motion of a rigid body whose axes of coordinates x, y, and z in the rotating reference system are matched with the main axes connected with the body, Euler’s dynamical equations have the form:

$$ \begin{gathered} {I_x}{{\dot{\omega}}_x}+\left( {{I_z}-{I_y}} \right){\omega_y}{\omega_z}={N_x}, \hfill \\ {I_y}{{\dot{\omega}}_y}+\left( {{I_x}-{I_z}} \right){\omega_x}{\omega_z}={N_y}, \hfill \\ {I_z}{{\dot{\omega}}_z}+\left( {{I_y}-{I_x}} \right){\omega_x}{\omega_y}={N_z}, \end{gathered} $$
(2.28)

where I x , I y , and I z are the moments of inertia of the body relative to the main axes; ω x , ω y , ω z , are the components of the instantaneous angular velocities on the axes; N x , N y , and N z are the main torques of the acting forces relative to the same axes; and \( {{\dot{\omega}}_x}, {{\dot{\omega}}_y}, \) and \( {{\dot{\omega}}_z} \) are the derivatives with respect to time from the angular velocities.

Euler’s kinematic equations are written as follows:

$$ \begin{aligned}[b] {\omega_x}= & \dot{\psi}\sin \theta \sin \varphi +\dot{\theta}\cos \varphi, \\ {\omega_y}= & \dot{\psi}\sin \theta \cos \varphi -\dot{\theta}\sin \varphi, \\ {\omega_z}= & \dot{\varphi}+\dot{\psi}\cos \theta . \end{aligned} $$
(2.29)

The Eulerian angles φ, ψ, and θ determine the position of a rigid body that has a fixed point relative to the fixed rectangular axes of coordinates. At hard linkage of the axes with the body and specification of the line of crossed planes of corresponding angles, they fix the rotation angle, the angle of precession, and the angle of nutation of the rotation axis.

For a uniform sphere, such as the Earth is according to Newton, I x  = I y  = I z.. Then the Eulerian equations of motion (2.28) acquire the form

$$ \begin{gathered} I{{\dot{\omega}}_x}=N{}_x, \hfill \\ I{{\dot{\omega}}_y}=N{}_y, \hfill \\ I{{\dot{\omega}}_z}=N{}_z.\end{gathered} $$
(2.30)

At free (inertial by Newton) rotation of the uniform Earth, which is not affected by the torque, N x  = N y  = N z  = 0. In that case, it follows from (2.30) that the components of the instantaneous velocities of their axes become constant and the angular velocity ω = const. Thus, angular velocity of a body at nonperturbed rotation is equal to a constant value.

Newton found that the Earth is flattened relative to the polar axis by centrifugal inertial force, and Clairaut has agreed with that. Then from the symmetry of the body having the form of an ellipsoid of rotation, it is found that N x  = N y  ≠ N z and only ω z  = const. From this in the case of absence of the outer torque, Eq. (2.28) is reduced to

$$ {{\dot{\omega}}_x}+\Omega {\omega_y}=0, $$
(2.31)
$$ {{\dot{\omega}}_y}-\Omega {\omega_x}=0, $$
(2.32)

where Ω is the angular velocity of free rotation, which at I x  = I y is equal to

$$ \Omega =\frac{{{I_z}-I{}_x}}{{{I_x}}}{\omega_z} $$
(2.33)

After transformation of Eqs. (2.31) to (2.32), one obtains their solution in the form of ordinary equations of the harmonic oscillation

$$ {\omega_x}=A\cos\,\Omega t, $$
(2.34)
$$ {\omega_z}=A\sin\,\Omega t, $$
(2.35)

where А is the constant value representing the amplitude of oscillation.

Thus, the component ω z of the angular velocity along the body’s axis of rotation is a constant value, and the component perpendicular to the axis is rotating with angular velocity Ω. So the whole body, while rotating by inertia relative to the geometric axis with angular velocity ω z , in accordance with (2.33) is wobbling with the frequency Ω. The oscillations described by Eqs. (2.34) and (2.35) are observed in reality and are called nutation of the rotating axis or a variation of latitude. The numerical value of the ratio of inertia moments (2.34) for the Earth is known and equal to

$$ {I_z}-{I_x}/{I_z}=0.0032732, $$

and the value of the angular velocity (free precession) is

$$ \Omega ={\omega_z}/305.5. $$

For the known value ω z  = 7.29 · 10−5 s−1, the period of Euler’s free precession is equal to 305 days or about 10 months. But analysis of the results of the long series of observations done by the American researcher Chandler has shown that, together with the annual component of the forced nutation, there is one more component having a period of about 420 days, which was called as free wobbling of the rotation axis. This component differs substantially from Euler’s free precession. The nature of the latter has not been understood up to now.

Euler also developed a complete theory of motion of the perfect liquid in hydromechanics, where differential equations in his variables become the basis for solution of hydrodynamic problems. Euler’s hydrodynamic equations for the perfect liquid in the rectangular Cartesian reference system x, y, z based on Newton’s equations of motion have the form

$$ \begin{gathered} \frac{{\partial u}}{{\partial t}}+u\frac{{\partial u}}{{\partial x}}+v\frac{{\partial u}}{{\partial y}}+\omega \frac{{\partial u}}{{\partial z}}=X-\frac{1}{\rho}\frac{{\partial p}}{{\partial x}}, \hfill \\ \frac{{\partial v}}{{\partial t}}+u\frac{{\partial v}}{{\partial x}}+v\frac{{\partial v}}{{\partial y}}+\omega \frac{{\partial v}}{{\partial z}}=Y-\frac{1}{\rho}\frac{{\partial p}}{{\partial y}}, \hfill \\ \frac{{\partial \omega }}{{\partial t}}+u\frac{{\partial \omega }}{{\partial x}}+v\frac{{\partial \omega }}{{\partial y}}+\omega \frac{{\partial \omega }}{{\partial z}}=Z-\frac{1}{\rho}\frac{{\partial p}}{{\partial z}},\end{gathered} $$
(2.36)

where u, v, and ω are the components of the velocity of liquid particles; p is the liquid pressure; ρ is the density; and X, Y, and Z are the components of the volumetric forces.

Solution of the hydrodynamic problems is reduced to determination of the components of velocities u, v, ω, the pressure and the density as a function of the coordinates with known values of X, Y, Z, and the given boundary conditions. For that purpose, in addition to Eq. (2.36), the equation of continuity is written in the form

$$ \frac{{\partial \rho }}{{\partial t}}+\frac{{\partial \left( {\rho u} \right)}}{{\partial x}}+\frac{{\partial \left( {\rho v} \right)}}{{\partial y}}+\frac{{\partial \left( {\rho \omega } \right)}}{{\partial z}}=0. $$
(2.37)

If the density of liquid depends only on pressure, then the extra equation of state will be presented by the relation ρ = f(p), and for the incompressible liquid, it is ρ = const.

Because the Earth is a system with continuous distribution of its masses, we will use the Eulerian hydrodynamic equations repeatedly.

2.4 Clausius’ Virial Theorem

Rudolf Clausius (1822–1888), a German physicist, is one of the founders of thermodynamics and the molecular kinetic theory of heat. Simultaneously with W. Thomson (Lord Kelvin), he has formulated the second law of thermodynamics in the following form: “Heat cannot be transferred by any continuous, self-sustaining process from a cold to a hotter body” without some changes, which should compensate that transfer. Clausius introduced the conception of entropy to thermodynamics.

In 1870, based on the study of the process and mechanism of Carnot’s thermal machine work, Clausius proved the virial theorem, according to which for a closed system the mean kinetic energy of the perfect gas particles’ motion is equal to half of their potential energy. The virial relation between the potential and kinetic energy was found to be a universal condition of the hydrostatic equilibrium for describing dynamics of the natural systems in all branches of physics and mechanics.

That equation was used first of all in the kinetic theory of gases for derivation of an equation of state for the perfect gases in the outer force field of the Earth; we assume that a specific perfect gas is found in a vessel of volume V and consists from N uniform particles (atoms or molecules). The mean kinetic energy of a particle of that gas at temperature T 0 is equal to 3kТ 0/2, where k is the Boltzmann’s constant. Then the virial theorem is written in the form

$$ -\frac{1}{2}\overline{{\sum\limits_i {{F_i}\cdot {r_i}} }}=\frac{3}{2}Nk{T_0}. $$
(2.38)

In this case, the effect of interaction of the gas atoms and molecules between themselves is negligibly small, and all the gas energy is realized by its interaction with the vessel’s wall. The gas pressure p inside the vessel appears only because of the walls, the elastic reaction of which plays the role of the inertial forces. The pressure is expressed through the energy of the molecules and atoms’ motion in the vessel, and expression (2.38) is written as the Clapeyron–Mendeleev equation of state for a perfect gas in the form

$$ \frac{3}{2}pV=\frac{3}{2}Nk{T_0}, $$

or

$$ pV=Nk{T_0}. $$
(2.39)

Equation (2.39) is the generalized expression of the laws of Boyle and Mariotte, Gay-Lussac, and Avogadro and represents the averaged virial theorem. Its left-hand side represents the potential energy of interaction of the gas particles, and the right-hand side is the kinetic energy of the gas pressure on the walls. In astrophysics, this equation is used as the equation of hydrostatic equilibrium state of a star, which is accepted as a gas and plasma system, where the gas pressure is equilibrated by the gravity forces of the attracted masses. In this case, the gravity forces play the role of the vessel’s walls or the outer force field, where the kinetic energy of motion of the interacted particles is not taken into account. Later on, it will be shown that for the natural gaseous and plasma self-gravitating systems, the only generalized virial equation can be used as the equation of state.

For celestial bodies including the Earth, other planets, and satellites, whose mass particles interact by the reverse square law and the forces of interaction are characterized by the potential U(r) as the uniform function of coordinates, the averaged virial theorem is reduced to the relation between the potential and kinetic energy in the form (Goldstein 1980)

$$ T=\frac{1}{2}\sum\limits_i {\overline{{\nabla U\cdot {r_i}}}} . $$
(2.40)

For a particle moving in the central force field expression (2.40) is

$$ T=\frac{1}{2}\frac{{\overline{{\partial U}}}}{{\mathrm{d}r}}r. $$
(2.41)

If U is the force function of r n, then

$$ T=\frac{n+1 }{2}\overline{U}. $$

Or, taking into account Euler’s theorem about the uniform functions and Newton’s law of interaction, when n = −2, one has

$$ T=-\frac{1}{2}\overline{U}. $$
(2.42)

Relationship (2.42) is valid only for a system that is found in the outer uniform force field. It expresses only mean values of the potential and kinetic energy per the period τ without effect of the inner kinetic energy of the interacting particles.

For a uniform sphere in outer uniform force field \( \rho F \) at inner isotropic pressure ρ, relation (2.42) represents the condition of hydrostatic equilibrium written by means of Euler’s equation in the form

$$ \frac{{\partial p}}{{\partial r}}=\rho {F_r}. $$

Here, the left-hand side of the equation is the potential energy, and the right-hand side represents the kinetic energy of the sphere in the framework of the averaged virial theorem.

It is clear that the averaged virial theorem in evolutionary dynamics is restricted by closed systems of a perfect gas, which corresponds to their hydrostatic equilibrium state.

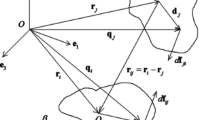
The general model of hydrostatic equilibrium based on a body’s outer central force field is shown in Fig. 2.2.

Fig. 2.2
figure 2

Conditions of hydrostatic equilibrium of a body based on the outer central gravity force field

Full size image

The problems of dynamics in the framework of hydrostatics cover also the tasks that consider a body under action of outer forces in elastic and viscous media of Hooke and Newton–Maxwell.

2.5 The Model of Hydrostatic Equilibrium of Elastic and Viscous-Elastic Body

The model of the Earth proposed by Newton and developed by Clairaut was in the form of a spheroid, rotating on inertia and filled in with uniform and nonuniform liquid, the mass of which resides in hydrostatic equilibrium in the outer force field. This model became generally accepted, commonly used, and in principal has not changed up to now. Its purpose was to solve the problem of the planet’s shape, that is, the form of the planet’s surface, and this goal was reached in the first approximation. Moreover, the equation obtained by Clairaut on surface changes in the acceleration of the gravity force as function of the Earth’s latitude opened the way for the experimental study of the oblateness of spheroid of rotation by means of measuring the outer gravity force field. Later on, in 1840, Stokes solved the direct and reverse task of determining the surface gravity force for a rotating body and above its level, applying the known parameters, namely, the mass, radius, and angular velocity. These parameters uniquely determined the gravity force at surface level, which is taken as the quiet ocean’s surface, and in all outer space. By that task, the relation between the Earth’s shape and the gravity force was determined. In the middle of the last century, Molodensky (1961) proposed the idea of considering the real surface of the Earth as a reduced surface and solved the corresponding boundary problem. The doctrine of the spheroidal figure of the Earth has found common understanding, and researchers, armed with theoretical knowledge, started to refine the dimensions and other details of the ellipsoid of rotation and to derive corresponding corrections.

Many publications were devoted to analysis of the observed inaccuracies in the Earth’s rotation together with explanation of their possible causes, based on experimental data and theoretical solutions. The most popular review work in the twentieth century was the book authored by the well-known English geophysicist Harold Jeffreys The Earth: Its Origin, History and Physical Constitution. The first publication of the book happened in 1922, and later four more editions appeared, including the last one in 1970. Jeffreys was a great expert and a direct participant of the development of the most important geophysical activities. The originality of his methodological approach in describing the material lies in that, after the formulation and theoretical consideration of the problem, he writes a chapter devoted to the experimental data and facts on the theme, the comparison with analytical solutions, and discussion.

Maintaining his position on Newton’s and Clairaut’s models, Jeffreys considers the planet as an elastic body and describes the equation of the force equilibrium from the hydrostatic pressure, which appears from the outer uniform central force field and exhibits strengths at a given point in the form

$$ \rho {f_i}=\rho {X_i}+\sum\limits_{k=1,2,3 } {\frac{{\partial p{}_{ik }}}{{\partial {x_k}}},} $$
(2.43)

where ρ is the density, f i is the acceleration component, p ik  = p ki is the stress component from the hydrostatic pressure, and Х i is the gravity force on the unit mass from the outer force field.

Additionally, the equation of continuity (like the continuity equation in hydrodynamics) is written as the condition of equality of velocity of the mass inflow and outflow from elementary volume in the form

$$ \frac{{\partial \rho }}{{\partial t}}=-\sum\limits_i {\frac{\partial }{{\partial {x_i}}}} \left( {\rho {v_i}} \right), $$
(2.44)

where v i is the velocity component in the direction of x i .

Further, applying the laws of elasticity theory, he expresses elastic properties of matter by the Lame coefficients and writes the basic equations of the strength state of the body, which links the strengths and the deformations in the point as

$$ \rho \frac{{{\partial^2}{u_i}}}{{\partial {t^2}}}=\left( {\lambda +\mu } \right)\frac{{\partial \varDelta }}{{\partial {x_i}}}+{\nabla^2}{u_i}, $$
(2.45)

where u i is the displacement component, λ and μ are the Lame coefficients, Δ is the component of the relative displacement, and \( \nabla \) is the Laplacian operator.

The author introduces a number of supplementary physical ideas related to the properties of the Earth’s matter, assuming that it is not perfectly elastic. With the development of stresses, matter reaches its limit of resistance and passes to the stage of plastic flow with a final effect of break in the matter’s continuity. This break leads to a sharp local change in the strength state, which, in turn, leads to the appearance of elastic waves in the planet’s body, causing earthquakes. For this case, Equation (2.45) after the same corresponding transformations is converted into the form of plane longitudinal and transversal waves, which propagate in all directions from the break place. Such is the physical basis of earthquakes, which was a starting point of development of seismology as a branch of geophysics studying the propagation of elastic longitudinal and transversal waves in the Earth’s body. By means of seismic study, mainly by strong earthquakes and based on difference in velocity of propagation of the longitudinal and transversal waves through the shells having different elastic properties, the shell-structured body of the planet was identified.

Jeffreys has analyzed the status of study in the theory of the shapes of the Earth and the Moon following Newton’s basic concepts. Namely, the planet has an inner and outer gravitational force field. The gravitational pressure is formed on the planet’s surface and affects the outer space and the planet’s center. The Earth’s shape is presented as an ellipsoid of rotation, which is perturbed from the side of inaccuracies in the density distribution, as well as from the side of the Moon’s perturbations. The problem is to find the axes of the ellipsoid under action of both perturbations which occur because of a difference in the gravity field for the real Earth and the spherical body. It is accepted that the oceans’ level is close to the spherical surface with deviation by a value of the first order of magnitude, and the geometric oblateness of the ellipsoid is close to the value of e ≈ 1/297. But the value squares of deviation cannot always be ignored because the value e 2 differs substantially from the value e. The observed data cannot be compared with theoretical solutions because the formulas depending on the latitudes give precise expressions neither for the radius vector from the Earth center to the sea level nor for the value of the gravity force. The problem of the planet’s mass density distribution finds its resolution from the condition of the hydrostatic pressure at a known velocity of rotation. The value of oblateness of the outer spheroid can be found from the observed value of the precession constant with a higher accuracy than one can find from the theory of the outer force field. A weak side of such approach is the condition of the hydrostatic stresses, which however are very small in comparison with the pressure at the center of the Earth. The author also notes that deviation of the outer planet’s gravitational field from spherical symmetry does not satisfy the condition of the inner hydrostatic stresses. Analysis of that discrepancy makes it possible to assess errors in the inner strengths related to the hydrostatics. Because of the Earth’s ellipticity, the attraction of the Sun and the Moon creates a force couple applied to the center, which forces the instantaneous axis of rotation to depict a cone around the pole of the ecliptic and to cause the precession phenomenon. The same effect initiates an analogous action on the Moon’s orbit

These are the main physical fundamentals that Jeffreys used for the analysis and theoretical consideration of the planet’s shape problem and for determination of its oblateness and of semimajor axis size. The author has found that the precession constant Н = 0.00327293 ± 0.00000075 and the oblateness 1/e = 297.299 ± 0.071. He assumes that these figures could be accepted as a result that gives the hydrostatic theory. But in conclusion, he says that the theory is not correct. If it is correct, then the solid Earth would be a benchmark of the planet’s surface covered by oceans. There are some other data confirming that conclusion. But this is the only and the most precise method for determining the spheroid flattening, which needs nonhydrostatic corrections to be found. Analogous conclusion was made by the author relative to the Moon’s oblateness, where the observed and calculated values are much more contrast.

The other review works on the irregularity of rotation and the pole motion of the Earth are the monographs of W. Munk and H. MacDonald (1960), P. Melchior, (1972–1973), and P. Sabadini and B. Vermeertsen (2004). The authors analyze there the state of the art and geophysical causes leading to the observed incorrectness in the planet’s rotation and wobbling of the poles. They draw the attention of the readers to the practical significance of the two main effects and designate about ten causes for their initiation. Among them are seasonal variations of the air masses, moving of the continents, melting and growing of the glaciers, elastic properties of the planet, and convective motion in the liquid core. The authors stressed that solution of any part of this geophysical task should satisfy the dynamical equations of motion of the rotating body and the equations, which determine a relationship between the stresses and deformations inside the body. The theoretical formulation and solution of a task should be considered on the hydrostatic basis, where the forces, inducing stresses, and deformations are formed by the outer uniform force field and the deformations occur in accordance with the theory of elasticity for the elastic body model, and in the framework of rheology laws for the elastic and viscous body model. The perturbation effects used are the wind force, the ocean currents, and the convective flows in the core and in the shells.

The causes of the axis rotation wobbling and the pole motion are considered in detail. The authors find that the problem of precession and nutation of the axis of rotation has been discussed for many years and does not generate any extra questions. The cause of the phenomena is explained by the Moon and the Sun perturbation of the Earth, which has an equatorial swelling and obliquity of the axis to the ecliptic. Euler equations for the rigid body form a theoretical basis for the problem’s solution. In this case, the free nutation of the rigid Earth according to Euler is equal to 10 months.

2.6 Evidences that the Earth and the Moon Move Being Not in Hydrostatic Equilibrium State

The effects of the Earth’s oblateness and the related problems of irregularity in the rotation and the planet’s pole motion and also the continuous changes in the gravity and electromagnetic field have a direct relation to the solution of a wide range of scientific and practical problems in the Earth dynamics, geophysics, geology, geodesy, oceanography, physics of the atmosphere, hydrology, and climatology. In order to understand the physical meaning and regularities of these phenomena, regular observations are carried out. Newton’s first attempts to find the quantitative value of the Earth’s oblateness were based on degree measurements done by Norwood, Pikar, and Kassini. As mentioned previously, by his calculation of the Paris latitude, the oblateness value appears to be 1/230. Very soon, some analogous measurements were taken in the equatorial zone in Peru and in the northern zone in Lapland Clairaut, Mopertui, and Buge, and other known astronomers also took part in these works. They confirmed the fact of the Earth’s oblateness as calculated by Newton. The degree of the arc in the northern latitudes appeared to be maximal, and the oblateness was equal to 1/214. In the equatorial zone, the arc length was minimal, and the oblateness was equal to 1/314. So the Earth pole axis from these measurements was found to be shorter of the equatorial approximately by 20 km.

As of the end of the first part of the twentieth century, more than 20 large degree measurements were done from which the values of the oblateness and dimension of the semimajor axes were found. The data of the measurements are presented in Table 2.1, and in Table 2.2, the parameters of the triaxial ellipsoid are shown (Grushinsky 1976).

Table 2.1 Parameters of the Earth’s oblateness by degree measurement data
Full size table
Table 2.2 Parameters or the Earth’s equatorial ellipsoid
Full size table

It is worth noting that in geodesy, a practical application of the triaxial ellipsoid has not been found, because it needs more complicated theoretical calculations and more reliable experimental data. In the theory, this important fact is ignored, because it is not inscribed into the hydrostatic theory of the body.

In addition to the local degree measurements, which allow determination of the Earth’s geometric oblateness, more precise integral data can be obtained by observation of the precession and nutation of the planet’s axis of rotation. It is assumed that the oblateness depends on deflection of the body’s mass density distribution from spherical symmetry and is initiated by a force couple that appeared to be an interaction of the Earth with the Moon and the Sun. The precession of the Earth’s axis is proportional to the ratio of the spheroid’s moments of inertia relative to the body’s axis of rotation in the form of the dynamical oblateness ε:

$$ \varepsilon =\frac{C-A }{C} $$

At the same time, the retrograde motion of the Moon’s nodes (points of the ecliptic intersection by the Moon orbit) is proportional to the second spherical harmonics coefficient J 2 of the Earth’s outer gravitational potential in the form

$$ {J_2}=\frac{C-A }{{M{a^2}}}. $$

It is difficult to obtain a rigorous value of geometric oblateness from its dynamic expression because we do not know the radial density distribution. Moreover, the Moon’s mass is known up to a fraction of a percent, but it is inconvenient to calculate analytically the joint action of the Moon and the Sun on the precession. In spite of that, some researchers succeeded in making such calculations, assuming that the Earth’s density is increasing proportionally to the depth. Their data are the following:

By Newcomb

ε = 1/305.32 = 0.0032753; e = 1/297.6;

By de Sitter

ε = 1/304.94 = 0.0032794; e = 1/297.6;

By Bullard

ε = 1/305.59 = 0.00327236; e = 1/297.34;

By Jeffreys

ε = 1/305.54 = 0.00327293; e = 1/297.3.

After appearance of the Earth’s artificial satellites and some special geodetic satellites, the situation with observation procedures has in principle changed. The satellites made it possible to determine directly, by measuring of the even zonal moments, the coefficient J n in expansion of the Earth gravitational potential by spherical functions. In this case at hydrostatic equilibrium, the odd and all the tesseral moments should be equal to zero. It was assumed before the satellite era that the correction coefficients of a higher degree of J 2 will decrease and the main expectations to improve the calculation results were focused on the coefficient J 4. But it has appeared that all the gravitational moments of higher degrees are the values proportional to square of oblateness, that is, ∼(1/300)2 (Zharkov 1978).

On the basis of the calculated harmonic, the coefficients of the expanded gravitational potential of the Earth published by Smithsonian Astrophysical observatory and the Goddard cosmic center of the USA, the fundamental parameters of the gravitational field, and the shape of the so-called standard Earth were determined. Among them are coefficient of the second zonal harmonic J 2 = 0.0010827, equatorial radius of the Earth ellipsoid а е = 6378160 m, angular velocity of the Earth’s rotation ω 3 = 7.292·10−5 rad/s, equatorial acceleration of the gravity force γ е = 978031.8 mgl, and oblateness 1/е = 1/298.25 (Grushinsky 1976; Melchior 1972). At the same time, if the Earth stays in hydrostatic equilibrium, then, applying the solutions of Clairaut and his followers, the planet’s geometric oblateness should be equal to e′ = 1/299.25. On the basis of that contradiction, Меlchior (1972) concluded that the Earth does not stay in hydrostatic equilibrium. It represents either a simple equilibrium of the rigid body, or there is equilibrium of a liquid and not static but dynamic with an extra hydrostatic pressure. Coming to interpretation of the density distribution inside the Earth by means of the Williamson–Adams equation, Меlchior (1972) adds that in order to eliminate there the hydrostatic equilibrium, one needs a supplementary equation. Since such an equation is absent, we are obliged to accept the previous conditions of hydrostatics.

The situation with the absence of hydrostatic equilibrium of the Moon is much more striking. The polar oblateness е р of the body is (Grushinsky 1976)

$$ {e_{\mathrm{p}}}=\frac{b-c }{{{r_0}}}=0.94\cdot 1{0^{-5 }}, $$

and the equatorial oblateness е е is equal

$$ {e_{\mathrm{e}}}=\frac{a-c }{{{r_0}}}=0.375\cdot 1{0^{-4 }}, $$

where а, b, and с are the equatorial and polar semiaxes and \( {r_0} \) is the body mean radius.

It was found by observation of the Moon libration that

$$ {e_{\mathrm{p}}}=4\cdot {10^{-4 }}\;\mathrm{and}\;{e_{\mathrm{e}}}=6.3\cdot {10^{-4 }}. $$

The calculation of the ratio of theoretical values of the dynamic oblateness e d = e p/e e = 0.25 substantially differs from the observation, which is 0.5 ≤ e d ≤ 0.75. At the same time, the difference of the semiaxes is \( {a_1}-{a_3}=1.03 \) km and \( {a_2}-{a_3}=0.83 \) km, where \( {a_1} \) and \( {a_2} \) are the Moon’s equatorial semiaxes.

After the works of Clairaut, Stokes, and Molodensky, on the basis of which the relationship between the gravity force change at the sea level and on the real Earth surface with the angular velocity of rotation was established, one more problem has risen. During measurements of the gravity force at any point of the Earth’s surface, two effects are revealed. The first is an anomaly of the gravity force, and the second is a declination of the plumb line from the normal in a given point.

Analysis of the gravity force anomalies and the geoid heights (a conventional surface of a quiet ocean) based on the existent schematic maps, compiled from the calculated coefficients of expansion of the Earth’s gravity potential and ground level gravimetric measurements, allows derivation of some specific features related to the parameter forming the planet. As Grushinsky (1976) notes, elevation of the geoid over the ellipsoid of rotation with the observed oblateness reaches 50–70 m only in particular points of the planet, namely, in the Bay of Biscay, North Atlantic, and near the Indonesian Archipelago. In the case of triaxial ellipsoid, the equatorial axis is passed near those regions with some asymmetry. The maximum of the geoid heights in the western part is shifted towards the northern latitudes and maximum in the eastern part remains in the equatorial zone. The western end of the major radius reaches the latitudes of 0–10° to the west of Greenwich, and the western end falls on the latitudes of about 30–40° to the west of a meridian of 180°. This also indicates asymmetry in distribution of the gravity forces and the forming masses. And the main feature is that the tendency to asymmetry of the northern and the southern hemispheres as a whole is observed. The region of the geoid’s northern pole rises above the ellipsoid up to 20 m, and the Antarctic region is situated lower by the same value. The asymmetry in planetary scale is traced from the northwest of Greenland to the southeast through Africa to the Antarctic with positive anomalies and from Scandinavia to Australia through the Indian Ocean with negative anomalies up to 50 mgl. Positive anomalies up to 30 mgl are fixed within the belt from Panama to Fiery Land and to the peninsula Grechem in the Antarctic. The negative anomalies are located on both sides, which extend from the Aleut bank to the southeast of the Pacific Ocean and from Labrador to the south of the Atlantics. The structure of the positive and negative anomalies is such that their nature can be interpreted as an effect of spiral curling of the northern hemisphere relative to the southern one.

As to the plumb line declination, this effect is considered only in geodesy from the point of view of practical application in the corresponding geodetic problems. Physical aspects of the problem are not touched. Later on, we will discuss this problem.

The problem of the Earth’s rotation has been discussed at the NATO workshop (Сazenave 1986). It was stated that both aspects of the problem still remain unsolved. The problems are variations in the day’s duration and the observed Chandler’s wobbling of the pole with the period of 14 months in comparison with 10 months, given by the Euler rigid body model. Chandler’s results are based on the analysis of 200-year observational data of motion of the Earth’s axis of rotation, done in the USA in the 1930s. He found that there is an effect of free wobbling of the planet’s axis with the period of about 420 days. Since that time, the discovered effect remains the main obstacle in the explanation of the nature and theoretical justification of the pole’s motion.

Summing up this short excursion to the problem’s history, we found the situation as follows. The majority of researchers dealing with the dynamics of the Earth and its shape come to the unanimous conclusion that the theories based on hydrostatics do not give satisfactory results in comparison with the observations. For instance, Jeffreys straightforwardly says that the theories are incorrect. Munk and MacDonald more delicately note that dozens of the observed effects can be called that do not satisfy the hydrostatic model. It means that the dynamics of the Earth as a theory is absent. This state of art and the conclusion motivated the authors to search for a novel physical basis for the dynamics and creation of the Earth, planets, and satellites. The first step in that direction was presented in their publication (Ferronsky and Ferronsky 2010).