Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Simulation of elastic multibody systems based on a finite element analysis has become usual in commercial multibody programs, such as MSC.Adams or SIMPACK. To model contacts between elastic bodies, the classical impact laws used in rigid-body dynamics, such as Newton’s kinematical approach or Poisson’s impact law [29] based on integrated forces, are not suitable. Instead contact models derived from the elastic body description have to be applied. Typically elastic body models are formulated by means of a modal approach like the Craig-Bampton method [12]. Modal functions describe the elastic deformations by a superposition of global mode shapes with static mode shapes or frequency response modes. However, the global mode shapes are not able to describe the elastic deformations of the bodies in the contact area. Consequently, the number of modes used for the contacting elastic bodies has to be increased. Another method to describe elastic contacts is the coupling between a finite element (FE) model and a multibody system (MBS), see [15]. As a FE body has typically a higher degree of freedom (DOF) than a complete MBS, the coupling of FE models and MBS results in a large computational amount.

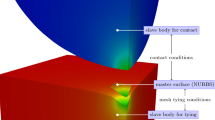
The aim of this chapter is to present a method to couple multibody systems with boundary element systems for contact simulation as shown in Fig. 1. This approach is seen as an alternative to model contact by coupled multibody/finite element simulations as presented by [2]. In this chapter three-dimensional problems are considered only. Due to the fact that three-dimensional contact algorithms for boundary element systems are sparely described in literature, a new contact element based on mortar methods has been developed, see [37].

Fig. 1
figure 1

Coupling of multibody system and boundary element models

Full size image

This contribution is organised as follows. In Sect. 2 the fundamentals of multibody systems are introduced. The description restricts on differential algebraic equations. Based on the boundary integral formulation for elastostatics introduced in Sect. 3, the Dirichlet-to-Neumann algorithm for contact calculation in boundary element systems is described in Sect. 4. This algorithm is based on mortar methods which are presented in Sect. 5. In Sect. 6 the numerical implementation of the mortar methods is described. The contact stresses are obtained from the contact calculation in boundary element systems. The calculation of the resulting contact force from the stresses is described in Sect. 7. As an example the dynamic simulation of two impacting spheres is presented in Sect. 8.

2 Fundamentals of Multibody Systems

In this section the theoretical background of multibody systems is shortly described. Due to the fact that the contact acts as a force element inside the multibody environment an introduction to constrained systems of rigid bodies is given only. The equations of motion are formulated as differential-algebraic equations (DAE). This formulation is typically used in commercial multibody simulation packages. A detailed description of multibody system dynamics is given in [32] and [35].

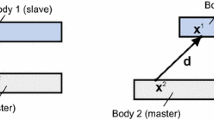
The position of the ith body of a constrained multibody system is described by a spatial vector \(\hat{\mathbf {r}}_{i}\) consisting of the position vector r i from an inertial system \(\mathcal{K}_{0}\) to a body-fixed coordinate system \(\mathcal{K}_{i}\) and m i ≥3 coordinates \(\mathbf {\gamma}_{i}\) describing the spatial orientation of \(\mathcal{K}_{i}\) relative to \(\mathcal{K}_{0}\) (Fig. 2),

$$ {\mathbf {\hat{r}}}_i = \left [ \begin{array}{c} {{\mathbf {r}}_i } \\ {{\mathbf {\gamma}}_i } \end{array} \right ]. $$
(1)

Examples for the definition of \(\mathbf {\gamma}_{i}\) are Euler angles or Euler parameters (unit quaternions). Accordingly, the absolute velocity of the ith body is described by the velocity v i and the angular velocity \(\mathbf {\omega}_{i}\) of \(\mathcal{K}_{i}\) put together in the six-dimensional spatial vector

$$ {\mathbf {\hat{v}}}_i = \left [ \begin{array}{c} {{\mathbf {v}}_i } \\ {{\mathbf {\omega}}_i } \end{array} \right ]. $$
(2)

To describe the position and velocity of the overall system with N bodies, the vectors

$$ {\mathbf {\hat{r}}} = \left [ \begin{array}{c} {{\mathbf {\hat{r}}}_1 } \\ \vdots\\ {{\mathbf {\hat{r}}}_{N} } \end{array} \right ], \qquad {\mathbf {\hat{v}}} = \left [ \begin{array}{c} {{\mathbf {\hat{v}}}_1 } \\ \vdots\\ {{\mathbf {\hat{v}}}_{N} } \end{array} \right ] $$
(3)

are introduced. The relation between the time derivatives of \(\hat {\mathbf {r}}_{i}\) and \(\hat{\mathbf {v}}_{i}\) is given by kinematic differential equations of the form

$$ \begin{aligned}[c] & {\mathbf {\dot{\hat{r}}}}_i = {\mathbf {{\widehat{H}}}}_i ({\mathbf {\hat{r}}}_i ) {\mathbf {\hat{v}}}_i, \quad i = 1, \ldots, N \\ & \mbox{or} \\ & {\mathbf {\dot{\hat{r}}}} = {\mathbf {{\widehat{H}}}} ({\mathbf {\hat{r}}} ){\mathbf {\hat{v}}}, \quad {\mathbf {{\widehat{H}}}} = \mathrm{diag}({\mathbf {{\widehat{H}}}}_1 \ldots {\mathbf {{\widehat{H}}}}_{N} ). \end{aligned} $$
(4)
Fig. 2
figure 2

Kinematics of rigid multibody systems

Full size image

The constraints between the rigid bodies at the position, velocity, and acceleration levels are formulated in the implicit form,

$$ {\mathbf {g}}({\mathbf {\hat{r}}},t) = {\mathbf {0}}, $$
(5)
$$ {\mathbf {\dot{g}}} \equiv{{ \mathbf {G}}}({\mathbf {\hat {r}}},t) {\mathbf { \hat{v}}} + {\mathbf {\bar{\dot{g}}}}({\mathbf {\hat{r}}},t) = {\mathbf {0}}, $$
(6)
$$ {\mathbf {\ddot{g}}} \equiv{{ \mathbf {G}}}({\mathbf {\hat {r}}},t) {\mathbf { \dot{\hat{v}}}} + {\mathbf {\bar{\ddot{g}}}}({\mathbf {\hat{r}}},{\mathbf {\hat{v}}}, t) = {\mathbf {0}}. $$
(7)

The kinetic differential equations are derived from the principles of linear momentum and angular momentum. Using spatial force vectors \(\hat{\mathbf {f}}_{i}\) containing a pair of a force and a torque the kinetic equations of the ith body are

$$ {\mathbf {\widehat{M}}}_i {\mathbf {\dot{ \hat{v}}}}_i = {\mathbf {\hat{f}}}_i^{\, \mathrm{c}} + {\mathbf { \hat{f}}}_i^{\, \mathrm{a}} + {\mathbf {\hat{f}}}_i^{\, \mathrm{r}} + {\mathbf {\hat{f}}}_i^{\,\mathrm{cc}}, \quad i = 1, \ldots,N, $$
(8)

with the symmetric, positive definite (6,6) mass matrix \({\mathbf {\widehat {M}}}_{i}\), gyroscopic and Coriolis forces \({\mathbf {\hat {f}}}_{i}^{\, \mathrm{c}}\), applied forces \({\mathbf {\hat{f}}}_{i}^{\, \mathrm{a}}\), and reaction forces (constraint forces) \({\mathbf {\hat{f}}}_{i}^{\,\mathrm {r}}\). Additionally, the vector \({\mathbf {\hat{f}}}_{i}^{\,\mathrm{cc}}\) is introduced to represent the contact forces. Inside the multibody environment, the contact force is represented by an applied force. The overall kinetic equations can be written as

$$ \begin{aligned}[b] & {\mathbf {\widehat{M}}} {\mathbf {\dot{\hat{v}}}} = {\mathbf {\hat {f}}}^{\, \mathrm {c}} + {\mathbf {\hat{f}}}^{\, \mathrm{a}} + {\mathbf {\hat{f}}}^{\, \mathrm{r}} + {\mathbf {\hat{f}}}^{\, \mathrm{cc}} \\ &\quad\mbox{with} \quad{\mathbf {\widehat{M}}} = \mathrm{diag}({\mathbf {\widehat {M}}}_1 \ldots{ \mathbf {\widehat{M}}}_{N} ), \quad {\mathbf {\hat{f}}}^{\, \mathrm{c/a/r/cc}} = \left [ \begin{array}{c} {{\mathbf {\hat{f}}}_1^{\, \mathrm{c/a/r/cc}} } \\ \vdots\\ {{\mathbf {\hat{f}}}_{N}^{\, \mathrm{c/a/r/cc}} } \end{array} \right ]. \end{aligned} $$
(9)

The reaction forces \({\mathbf {\hat{f}}}_{i}^{\, \mathrm{r}}\) have components in the constrained spatial directions only, given by the row vectors of the constraint matrix G from (6). Accordingly, they can be expressed by means of the explicit reaction force equations

$$ {\mathbf {\hat{f}}}^{\, \mathrm{r}} = \mathbf {G}^{\mathrm{T}} \boldsymbol{\lambda} $$
(10)

with reaction force coordinates (Lagrangian multipliers) λ. If the positions \({\mathbf {\hat{r}}}\) and the velocities \({\mathbf {\hat{v}}}\), which have to be consistent with the constraints (5) and their first-order time derivatives (6), are given, (9) with (10) and (7) together represent a set of linear equations to determine uniquely the accelerations \({{\mathbf {\dot{\hat{v}}}}}\) and the reaction force coordinates λ,

$$ \left [ \begin{array}{c@{\quad}c} {\mathbf {\widehat{M}}} & \mathbf {G}^{\mathrm{T} } \\ {\mathbf {G}} & {\mathbf {0}} \end{array} \right ] \cdot \left [ \begin{array}{c} {{\mathbf {\dot{\hat{v}}}}} \\ { - \boldsymbol{\lambda}} \end{array} \right ] = \left [ \begin{array}{c} {{\mathbf {\hat{f}}}}^{\, \mathrm{c}} + {\mathbf {\hat{f}}}^{\, \mathrm {a}} + {{\mathbf {\hat{f}}}}^{\, \mathrm{cc}} \\ { - {\mathbf {\bar{\ddot{g}}}}} \end{array} \right ]. $$
(11)

Numerical integration of the velocity \({\mathbf {\hat{v}}}\) obtained from the kinematic differential equation (4) and of the acceleration \({\mathbf {\dot{\hat{v}}}}\) obtained from (11) yields the motion of the system, described by the position \({\mathbf {\hat {r}}}(t)\) and the velocity \({\mathbf {\hat{v}}}(t)\). The reaction force coordinates λ obtained from (11) yield the reaction forces \({{\mathbf {\hat{f}}}}^{\, \mathrm{r}}\) by means of the explicit reaction force equations (10). During numerical integration, the constraints at the position and velocity levels may be violated necessitating a constraint stabilisation [4].

3 Boundary Integral Formulation in Elastostatics

The boundary integral formulation starts from the partial differential equation representing the quasistatic equilibrium inside the volume V,

$$ \sigma_{ij,j} + b_i = 0 \quad \mbox{in } V \quad\mbox{for } i = x, y, z. $$
(12)

Herein the variable σ ij represents the stress tensor inside the volume V and b i the body forces due to the acceleration of the body. In addition to the equilibrium inside the volume V, the equilibrium conditions on the surface S,

$$ t_i = \sigma_{ij} n_j \quad \mbox{on }S, $$
(13)

have to be fulfilled. Herein t i is the stress vector, also called traction vector, representing the equilibrium on the surface S with the outward normal vector n j .

The surface is divided into regions with different types of boundary conditions. There are regions on the surface S where the Dirichlet boundary conditions

$$ u_i = \bar{u}_i \quad \mbox{on } S_u $$
(14)

have to be fulfilled, and regions with Neumann boundary conditions,

$$ t_i = \bar{t}_i \quad \mbox{on } S_t. $$
(15)

Due to the fact that each point on the surface S has three degrees of freedom, each direction i=x,y,z has to be treated separately. Thus, the requirements S i =S ui ∪S ti and S ui ∩S ti =0 have to be fulfilled for each coordinate direction i.

By using the weighted residual formulation

$$ \int _V { ( {\sigma_{ij,j} + b_i } )} \,w_i \,{\mathrm{d}} \tilde{V} + \int _{S_u} { ( {u_i - \bar{u}_i } )} \bar{w}_i \,{ \mathrm{d}} \tilde{S} + \int _{S_t} { ( {t_i - \bar{t}_i } )} \tilde{w}_i \,{\mathrm{d}} \tilde{S} = 0 $$
(16)

and introducing the fundamental solutions \(u_{ij}^{*}\) and \(t_{ij}^{*}\) as weighting functions, the Somigliana identity

$$ u_i(\mathbf {x}) = \int _S {u_{ij}^*( \mathbf {x}, \mathbf {y}) t_j (\mathbf {y}) } \, {\mathrm{d}} \tilde{S} - \int _S {t_{ij}^*(\mathbf {x}, \mathbf {y}) u_j (\mathbf {y}) }\, {\mathrm{d}} \tilde{S} + \int _V {u_{ij}^*( \mathbf {x}, \mathbf {y}) b_j (\mathbf {y}) } \, {\mathrm{d}} \tilde{V} $$
(17)

is obtained which is valid for an arbitrary load point x inside the volume V. The fundamental solutions for elastostatics have been developed by Lord Kelvin, see [33]. They represent the response of the system at any arbitrary field point y due to a unit load at a chosen load point x. In this chapter, three-dimensional boundary element formulations are treated only. Because each point has three degrees of freedom, the coordinate direction has also to be considered. A volume integral with the specific body forces b j is given on the left hand side of (17).

According to [1], the displacement fundamental solution, also called Dirichlet fundamental solution, at a field point y in direction j due to a unit load at a load point x in direction i is given by

$$ u_{ij}^* ({\mathbf {x}},{\mathbf {y}}) = \frac{{1 + \nu}}{{8\pi E(1 - \nu )r}} \bigl[ { ( {3 - 4 \nu} ){{\delta}}_{ij} + r,_i r,_j } \bigr]. $$
(18)

Herein, the variable E represents Young’s modulus, ν Poisson’s ratio, and δ ij the Kronecker delta. The distance r between a load point x and a field point y is given by the Euclidian norm

$$ r = \Vert \mathbf {y} - \mathbf {x} \Vert . $$
(19)

The partial derivatives of the Euclidian distance r with respect to the coordinate direction i can easily be obtained by

$$ r,_i = \frac{y_i - x_i}{r}. $$
(20)

The stress fundamental solution, also known as Neumann fundamental solution, at a field point y in direction j due to a unit load at a load point x in direction i is given by

(21)

where n i represents the ith component of the outward normal vector n. Herein, the derivative in normal direction is calculated by

$$ \frac{{\partial r}}{{\partial n}} = r,_i n_i. $$
(22)

According to the third summand in (17), a remaining volume integral with the specific body forces b j has to be taken into account. There are different procedures to calculate body forces. A method is the discretisation of the volume by using cells, see [1]. For a boundary element formulation this method is less appropriate because an additional volume mesh has to be introduced. A proposal for the transformation of the body forces from the volume V on the surface S was made in [13]. In the present chapter, quasistatic body forces are taken into account only. By this, elastic vibrations of the body are neglected.

Starting from Somigliana’s identity (17) for a load point x on the surface S, the integral equation under consideration of the boundary factor c ij is given by

$$ c_{ij} u_j(\mathbf {x}) = \int _S {u_{ij}^*(\mathbf {x}, \mathbf {y}) t_j (\mathbf {y}) }\, {\mathrm{d}} \tilde{S} - \int _S {t_{ij}^*(\mathbf {x}, \mathbf {y}) u_j (\mathbf {y}) }\, {\mathrm{d}} \tilde{S} + B_i(\mathbf {x}). $$
(23)

The boundary factor c ij is a correction factor to consider load points on the surface S of the volume V. Due to the introduction of surface elements, the surface integrals in (23) are evaluated element-wise (summation over all elements e),

$$ c_{ij} u_j(\mathbf {x}) = \sum _e \int _{S_e} {u_{ij}^*(\mathbf {x}, \mathbf {y}) t_j (\mathbf {y}) }\, {\mathrm{d}} \tilde{S} - \sum _e \int _{S_e} {t_{ij}^*(\mathbf {x}, \mathbf {y}) u_j (\mathbf {y}) }\, {\mathrm{d}} \tilde{S} + \sum _e B_{ie}(\mathbf {x}). $$
(24)

The continuous functions u j (y) for the displacements and t j (y) for the tractions can be replaced by discrete nodal values which leads to

$$ u_j (\mathbf {y}) = N_k \bigl( \mathbf {y} (\xi, \eta) \bigr) u_{kj} \quad\mbox{and} \quad t_j (\mathbf {y}) = N_k \bigl( \mathbf {y} (\xi, \eta) \bigr) t_{kj}. $$
(25)

Herein, ξ and η are the local element coordinates. The index k represents the kth node of element e and j represents one of the coordinate directions x, y, or z. Caused by the fact that the values u kj and t kj can belong to more than one element, it is necessary to replace the summation over all elements e in (24) by an assembly,

$$ \begin{aligned}[b] c_{ij} N_k \bigl( \mathbf {x} (\xi, \eta) \bigr) u_{kj} = & \bigcup_e \int _{S_e} {u_{ij}^*\bigl(\mathbf {x}, \mathbf {y} (\xi, \eta)\bigr) N_k \bigl( \mathbf {y} (\xi, \eta) \bigr) }\, \mathrm{d} \tilde{S} \, t_{kj} \\ &{} - \bigcup_e \int _{S_e} {t_{ij}^*\bigl(\mathbf {x}, \mathbf {y} (\xi, \eta)\bigr) N_k \bigl( \mathbf {y} (\xi, \eta) \bigr)}\, {\mathrm{d}} \tilde{S} \, u_{kj} + {\sum _e} B_{ie}(\mathbf {x}). \end{aligned} $$
(26)

Within this chapter, collocation methods are applied to obtain a discretised system of equations from (26). Assuming that the body is discretised by n nodes, the load point x is set to the location of each node x l with l=1,…,n. That means, instead of the arbitrary load point x in (26), the nodal coordinates x l of the discretised geometry are used as collocation points leading to

$$ \begin{array}[c]{r@{\,}ll} c_{ij} u_{1j} &=& \displaystyle \bigcup_e \int_{S_e} {u_{ij}^*\bigl(\mathbf {x}_1, \mathbf {y}(\xi, \eta)\bigr) N_k \bigl( \mathbf {y} (\xi, \eta) \bigr) }\, {\mathrm{d}} \tilde{S} \, t_{kj} \\ \noalign{\vspace*{3pt}} &&{} - \displaystyle\bigcup_e \int_{S_e} {t_{ij}^*\bigl(\mathbf {x}_1, \mathbf {y}(\xi, \eta)\bigr) N_k \bigl( \mathbf {y} (\xi, \eta) \bigr)} \,{ \mathrm{d}} \tilde{S} \, u_{kj} + {\sum_e} B_{ie}(\mathbf {x}_1), \\ \noalign{\vspace*{3pt}} &\vdots& \\ \noalign{\vspace*{3pt}} c_{ij} u_{lj} &=& \displaystyle\bigcup _e \int_{S_e} {u_{ij}^* \bigl(\mathbf {x}_l, \mathbf {y}(\xi, \eta)\bigr) N_k \bigl( \mathbf {y} (\xi, \eta) \bigr) }\, {\mathrm{d}} \tilde{S} \, t_{kj} \\ \noalign{\vspace*{3pt}} &&{} - \displaystyle\bigcup_e \int_{S_e} {t_{ij}^*\bigl(\mathbf {x}_l, \mathbf {y}(\xi, \eta)\bigr) N_k \bigl( \mathbf {y} (\xi, \eta) \bigr)}\, { \mathrm{d}} \tilde{S} \, u_{kj} + {\sum_e} B_{ie}(\mathbf {x}_l), \\ \noalign{\vspace*{3pt}} &\vdots& \\ \noalign{\vspace*{3pt}} c_{ij} u_{nj} &=& \displaystyle\bigcup _e \int_{S_e} {u_{ij}^* \bigl(\mathbf {x}_{n}, \mathbf {y}(\xi, \eta)\bigr) N_k \bigl( \mathbf {y} (\xi, \eta) \bigr) }\, {\mathrm{d}} \tilde{S} \, t_{kj} \\ \noalign{\vspace*{3pt}} &&{} - \displaystyle\bigcup_e \int_{S_e} {t_{ij}^*\bigl(\mathbf {x}_{n}, \mathbf {y}(\xi, \eta)\bigr) N_k \bigl( \mathbf {y} (\xi, \eta) \bigr)}\, { \mathrm{d}} \tilde{S} \, u_{kj} + {\sum_e} B_{ie}(\mathbf {x}_{n}). \end{array} $$
(27)

The integrals from (27) can be evaluated with respect to the element surface S e . By assembling (27) over all elements e, the system of equations

$$ \bigl( \mathbf {C} + \mathbf {H}^* \bigr) \mathbf {u} = \mathbf {G} \mathbf {t} + \mathbf {B} $$
(28)

is obtained. Herein, the matrix C contains the boundary factors c ij . According to (27), this matrix is block diagonal. Due to the use of the fundamental solutions \(u_{ij}^{*}\) and \(t_{ij}^{*}\), the matrices H ∗ and G are fully populated, unsymmetrical and not necessarily positive definite. The vector B contains the projected body forces. The system of equations (28) can be written as

$$ \mathbf {H} \mathbf {u} = \mathbf {G} \mathbf {t} + \mathbf {B} $$
(29)

which is the form known from literature [1, 5, 17].

4 Contact Calculation by a Dirichlet-to-Neumann Algorithm

This contribution presents an extension to the Lagrangian multiplier approach introduced in [42]. The algorithm is introduced to reduce the amount of random access memory and to decrease the calculation time for large systems. The algorithm presented here is based on [25] and [38]. The principle of this Dirichlet-to-Neumann algorithm which is called a nonlinear Gauss-Seidel block in [24] is shown in Fig. 3.

Fig. 3
figure 3

Principle of Dirichlet-to-Neumann algorithm

Full size image

The two contacting bodies are divided into a Neumann body and a Dirichlet body. In this chapter the mortar and non-mortar are equivalent to the Neumann and Dirichlet body, respectively. Within each iteration, a linear Neumann problem and a nonlinear Dirichlet problem is solved. Starting from (29), the system of equations for the Neumann body can be expressed by

$$ {\mathbf {H}}^{\mathrm{N}} \Delta {\mathbf {u}}^{{\mathrm{N}}(j)} = {\mathbf {G}}^{\mathrm{N}} \Delta {\mathbf {t}}^{{\mathrm{N}}(j)} + {\mathbf {B}}^{{\mathrm {N}}(j)}, $$
(30)

where the index j represents the iteration step within the Dirichlet-to-Neumann algorithm and the upper right index N denotes the Neumann body. The system of equations can be partitioned into degrees of freedom that are in contact and such that are not,

$$ \left [ \begin{array}{c@{\quad}c} {{\mathbf {H}}_{\mathrm{nc}}^{\mathrm{N}} } & {{\mathbf {H}}_{\mathrm{cc}}^{\mathrm{N}} } \end{array} \right ]\left [ \begin{array}{c} \Delta {\mathbf {u}}_{\mathrm{nc}}^{{\mathrm{N}}(j)} \\[3pt] \Delta {\mathbf {u}}_{\mathrm{cc}}^{{\mathrm{N}}(j)} \end{array} \right ] = \left [ \begin{array}{c@{\quad}c} {{\mathbf {G}}_{\mathrm{nc}}^{\mathrm{N}} } & {{\mathbf {G}}_{\mathrm{cc}}^{\mathrm{N}} } \end{array} \right ]\left [ \begin{array}{c} \Delta {\mathbf {t}}_{\mathrm{nc}}^{{\mathrm{N}}(j)} \\[3pt] \Delta {\mathbf {t}}_{\mathrm{cc}}^{{\mathrm{N}}(j)} \end{array} \right ] + {\mathbf {B}}^{{\mathrm{N}}(j)}. $$
(31)

Herein, the degrees of freedom which are not in contact are denoted by the lower right indices nc and those which are in contact by cc, respectively. The body forces B N(j) are typically applied within the first iteration, that means \({\mathbf {B}}^{{\mathrm{N}}(j)} \stackrel{!}{=} \mathbf {0}\) for j>1. As indicated by the name of the algorithm, the tractions caused by the contact are applied to the Neumann body, where for the first iteration step, thus j=1, the contact tractions \(\Delta {{\mathbf {t}}_{\mathrm{cc}}^{{\mathrm{N}}(1)} }\) are assumed to be zero. Considering also the other boundary conditions in the non-contact area and sorting the system of equations (31) with respect to known and unknown values leads to

$$ \left [ \begin{array}{c@{\quad}c@{\quad}c} { - {\mathbf {G}}_{\mathrm{ncD}}^{\mathrm{N}} } & {{\mathbf {H}}_{\mathrm{\mathrm{ncN}}}^{\mathrm {N}} } & {{\mathbf {H}}_{\mathrm{cc}}^{\mathrm{N}} } \end{array} \right ]\left [ \begin{array}{c} \Delta {{\mathbf {t}}_{\mathrm{ncD}}^{{\mathrm{N}}(j)} } \\ [3pt] \Delta {{\mathbf {u}}_{\mathrm{\mathrm{ncN}}}^{{\mathrm{N}}(j)} } \\ [3pt] \Delta {{\mathbf {u}}_{\mathrm{cc}}^{{\mathrm{N}}(j)} } \end{array} \right ] = \left [ \begin{array}{c@{\quad\!}c@{\quad\!}c} { - {\mathbf {H}}_{\mathrm{ncD}}^{\mathrm{N}} } & {{\mathbf {G}}_{\mathrm{\mathrm{ncN}}}^{\mathrm {N}} } & { {\mathbf {G}}_{\mathrm{cc}}^{\mathrm{N}} } \end{array} \right ]\left [ \begin{array}{c} \Delta {{\mathbf {u}}_{\mathrm{ncD}}^{{\mathrm{N}}(j)} } \\[3pt] \Delta {{\mathbf {t}}_{\mathrm{\mathrm{ncN}}}^{{\mathrm{N}}(j)} } \\[3pt] \Delta {{\mathbf {t}}_{\mathrm{cc}}^{{\mathrm{N}}(j)} } \end{array} \right ] + {\mathbf {B}}^{{\mathrm{N}}(j)}. $$
(32)

Equation (32) represents a fully populated quadrangular system of equation of the form A N x N=b N which can be solved by Gauss or LU decomposition. The deformed mesh of the Neumann body is stored after each iteration and acts as rigid obstacle for the Dirichlet body. In order to obtain the overall deformations and tractions the incremental deformations Δu N(j) and tractions Δt N(j) are summarised over all iterations j. According to [25] a numerical damping parameter δ D with 0<δ D≤1 is introduced, resulting in

$$ {\mathbf {u}}^{{\mathrm{N}}(j)} = {\mathbf {u}}^{{\mathrm{N}}(j-1)} + {{\delta}}_{\mathrm {D}} \Delta {\mathbf {u}}^{{\mathrm{N}}(j)} \quad\mbox{and} \quad{ \mathbf {t}}^{{\mathrm{N}}(j)} = {\mathbf {t}}^{{\mathrm{N}}(j-1)} + {{\delta}}_{\mathrm {D}} \Delta {\mathbf {t}}^{{\mathrm{N}}(j)}. $$
(33)

The actual nodal coordinates of the Neumann body are obtained by

$$ \mathbf {x}^{{\mathrm{N}}(j)} = \mathbf {x}^{{\mathrm{N}}(j-1)} + {{\delta }}_{\mathrm{D}} \Delta{{ \mathbf {u}}^{{\mathrm{N}}(j)}}. $$
(34)

The second step within each iteration is the solution of a nonlinear Dirichlet problem. The formulation starts from the system of equations

$$ {\mathbf {H}}^{\mathrm{D}} {\mathbf {u}}^{{\mathrm{D}}(j)} = {\mathbf {G}}^{\mathrm{D}} {\mathbf {t}}^{{\mathrm{D}}(j)} + {\mathbf {B}}^{\mathrm{D}}, $$
(35)

where the upper right index D denotes the Dirichlet body and j the number of iteration. Comparing (30) and (35) differences can be determined between the systems of equations of the Neumann and the Dirichlet body. The calculation of the Dirichlet body always starts from the reference configuration x D(1) within each iteration step j, which means in general the undeformed configuration. Hence, no incremental update has to be done for the displacements u D(j) and t D(j). The body forces B D have to be applied within each iteration step or by superposition once in a preprocessing step.

The system of equations (35) can be partitioned and sorted leading to

$$ \left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} { - {\mathbf {G}}_{\mathrm{ncD}}^{\mathrm{D}} } & {{\mathbf {H}}_{\mathrm{\mathrm{ncN}}}^{\mathrm {D}} } & {{\mathbf {H}}_{\mathrm{cc}}^{\mathrm{D}} } & { - {\mathbf {G}}_{\mathrm{cc}}^{\mathrm{D}}} \end{array} \right ]\left [ \begin{array}{c} {{\mathbf {t}}_{\mathrm{ncD}}^{{\mathrm{D}}(j)} } \\[3pt] {{\mathbf {u}}_{\mathrm{\mathrm{ncN}}}^{{\mathrm{D}}(j)} } \\[3pt] {{\mathbf {u}}_{\mathrm{cc}}^{{\mathrm{D}}(j)} } \\[3pt] {{\mathbf {t}}_{\mathrm{cc}}^{{\mathrm{D}}(j)} } \end{array} \right ] = \left [ \begin{array}{c@{\quad}c} { - {\mathbf {H}}_{\mathrm{ncD}}^{\mathrm{D}} } & {{\mathbf {G}}_{\mathrm{\mathrm{ncN}}}^{\mathrm {D}} } \end{array} \right ]\left [ \begin{array}{c} {{\mathbf {u}}_{\mathrm{ncD}}^{{\mathrm{D}}(j)} } \\ [3pt] {{\mathbf {t}}_{\mathrm{\mathrm{ncN}}}^{{\mathrm{D}}(j)} } \end{array} \right ] + {\mathbf {B}}^{\mathrm{D}}, $$
(36)

which represents a system of linear equations of the form A D x D(j)=b D(j). Due to the fact that within the potential contact area the displacements \({{\mathbf {u}}_{\mathrm{cc}}^{{\mathrm{D}}(j)} }\) and the tractions \({{\mathbf {t}}_{\mathrm {cc}}^{{\mathrm{D}}(j)} }\) are unknown, the system of equations (36) is rectangular, that means the number of equations is lower than the number of unknown nodal values. This results in an infinite number of possible solutions.

To solve (36), a quadratic optimisation problem with equality and inequality constraints is formulated,

$$ \begin{aligned}[b] & \frac{1}{2} \mathbf {x}^{{\mathrm{D}}(j)\mathrm{T}} \mathbf {Q}^{{\mathrm{D}}(j)} \mathbf {x}^{{\mathrm{D}}(j)} + \mathbf {x}^{{\mathrm{D}}(j)\mathrm{T}} \mathbf {p}^{{\mathrm{D}}(j)} = \min_{\mathbf {x}^{{\mathrm{D}}(j)}} \\ & \quad\mbox{subject to} \quad \mathbf {A}^{\mathrm{D}} \mathbf {x}^{{\mathrm {D}}(j)} = \mathbf {b}^{{\mathrm{D}}(j)} \quad\mbox{and} \quad \mathbf {N}^{{\mathrm {D}}(j)} \mathbf {x}^{{\mathrm{D}}(j)} + \mathbf {d}_0^{{\mathrm{D}}(j)} \geq \mathbf {0}. \end{aligned} $$
(37)

Herein Q D(j) represents the objective function matrix containing the weighting factors of the nodal values x D(j), and p D(j) contains the coefficients of the linear part of the quadratic objective function. Typically, Q D(j) is a unit matrix, and the elements of p D(j) are zero. If the objective function matrix Q D(j) is equal to the identity matrix, the result of such an optimisation is identical to the Moore-Penrose inverse of the left-hand side matrix A D given in (36). As equality condition the system of equations (36) is used. The inequality equations \(\mathbf {N}^{{\mathrm{D}}(j)} \mathbf {x}^{{\mathrm {D}}(j)} + \mathbf {d}_{0}^{{\mathrm{D}}(j)} \geq \mathbf {0}\) represent the one-sided constraints which are built up with respect to the deformed surface of the Neumann body representing the mortar side of the contacting bodies. The matrix N D(j) containing the normal vectors and the vector \(\mathbf {d}_{0}^{{\mathrm{D}}(j)}\) containing the initial gaps have to be built up within each iteration step j.

The theoretical background and computational implementation of the quadratic programming is not explained here. A description and implementation on that topic is given by [26].

If the optimisation is successful, the reaction forces in form of the tractions \({\mathbf {t}}_{\mathrm{cc}}^{{\mathrm{D}}(j)}\) are obtained. The sum of the tractions inside the contact area has to vanish,

$$ {\mathbf {t}}_{\mathrm{cc}}^{{\mathrm{D}}(j)} + {\mathbf {t}}_{\mathrm{cc}}^{{\mathrm{N}}(j)} = {\mathbf {0}}. $$
(38)

Because of the possibility of nonconforming meshes of the contacting bodies, dynamic constraints based on a mortar method not explained so far are introduced. This leads to a reformulation of (38),

$$ {\mathbf {M}}_t^{{\mathrm{D}}(j)} {\mathbf {t}}_{\mathrm{cc}}^{{\mathrm{D}}(j)} + {\mathbf {M}}_t^{{\mathrm{N}}(j)} {\mathbf {t}}_{\mathrm{cc}}^{{\mathrm{N}}(j)} = {\mathbf {0}}, \quad{\mathbf {0}} \in\mathbb{R}^{\mathrm{N}}, $$
(39)

where the mortar matrices \({\mathbf {M}}_{t}^{{\mathrm{D}}(j)}\) and \({\mathbf {M}}_{t}^{{\mathrm{N}}(j)}\) have to be built up within each iteration based on the actual geometry of the Neumann body as it will be shown in Sect. 5. Due to the fact that mortar matrices are formed with respect to the degrees of freedom in contact on the Neumann body representing the mortar side, the matrix \({\mathbf {M}}_{t}^{{\mathrm{N}}(j)}\) is quadratic and has a full rank. Inversion of the matrix \({\mathbf {M}}_{t}^{{\mathrm{N}}(j)}\) in (39) leads to

$$ {\mathbf {t}}_{\mathrm{cc}}^{{\mathrm{N}}(j)} = -{\mathbf {M}}_t^{{\mathrm {N}}(j)-1} {\mathbf {M}}_t^{{\mathrm{D}}(j)} {\mathbf {t}}_{\mathrm{cc}}^{{\mathrm{D}}(j)}, $$
(40)

which represents a mapping of the tractions in the contact area from the Dirichlet body to the Neumann body. Because the system of equations (30) is given in an incremental form, the incremental tractions \(\Delta {\mathbf {t}}_{\mathrm{cc}}^{{\mathrm{N}}(j)}\) are calculated by

$$ \Delta {\mathbf {t}}_{\mathrm{cc}}^{{\mathrm{N}}(j)} = {{\delta }}_{\mathrm{N}} \bigl( {\mathbf {t}}_{\mathrm{cc}}^{{\mathrm{N}}(j)}-{\mathbf {t}}_{\mathrm{cc}}^{{\mathrm {N}}(j-1)} \bigr), $$
(41)

where δ N is an additional numerical damping parameter with 0<δ N≤1. For further information on building up mortar matrices see Sect. 5. A summary of the global solution algorithm is given in Algorithm 1.

Algorithm 1
figure 4

Dirichlet-to-Neumann algorithm

Full size image

Note that if the damping parameters δ D in (36) and δ N in (41) are equal to 1, no convergence will be achieved. In [25] it is suggested to choose 0.7 for δ D and δ N. A value of 1.0 for the parameter δ D and a value of 0.5 for the parameter δ N for the algorithm described above is recommended. Due to the fact that the surface tractions are calculated, fast convergence is achieved if the half of the tractions are transferred from the Dirichlet body to the Neumann body.

5 Build-up of Mortar Matrices

In this section the theoretical background of the mortar methods for contact and the numerical implementation to create the mortar matrices M t and M u from (39) are described. The aim of the mortar methods is to find a mapping matrix between the degrees of freedom of the contacting bodies. The basic concept presented here was published by [30] for finite elements. It is here adapted for boundary elements. Similar to Fig. 3, the contacting bodies are divided into a mortar and non-mortar body, denoted by the indices m and nm, respectively, that are equivalent to the Neumann body and the Dirichlet body, respectively.

As mentioned before, mortar contact belongs to the group of contacts which is based on Lagrangian multipliers. The unilateral constraint for contact formulation can be defined using the Kuhn-Tucker-Karush conditions,

$$ \begin{array}[c]{l@{\qquad}l@{\qquad}l@{\qquad}l} \mbox{1-dimensional}& d \ge 0 & \lambda \le0 & \lambda d = 0, \\[3pt] \mbox{2- or 3-dimensional}& {\mathbf {d}} \ge{ \mathbf {0}} & \boldsymbol{\lambda} \le{ \mathbf {0}} & \boldsymbol{\lambda}^{\mathrm{T}} {\mathbf {d}} = 0. \end{array} $$
(42)

The first line of (42) presents the constraints for one-dimensional problems. As the gap cannot be negative, d≥0, and only pressure forces can be transferred, λ≤0, the product of the gap d and the Lagrangian multiplier λ always vanishes.

For two- and three-dimensional problems typically a distinction has to be made between normal and tangential contact. For normal contact, the same constraints as for one-dimensional contact can be used where vectors of the gap d and of the Lagrangian multiplier λ have to be projected in normal direction. Stiction and sliding may occur in tangential direction. In case of sliding, the tangential forces act as applied forces in opposite directions of the relative motion so that force laws such as Coulomb’s law can be applied. In case of stiction, no motion in tangential direction occurs. In that case, the tangential contact can also be treated as a constraint and the resulting tangential tractions have to be treated as reaction stresses. Hence, the normal and tangential contact can be summarised according to the second line of (42).

The starting point for building up three-dimensional mortar matrices is the weak form of the Kuhn-Tucker-Karush condition,

$$ \varPi_{\mathrm{c}}^{\mathrm{LM}} = \int _{S_{\mathrm{cc}} } \boldsymbol{\lambda}^{\mathrm{T}} \mathbf{d} \, \mathrm{d} S. $$
(43)

Due to the weak form, the constraints are fulfilled in an integral meaning over the potential contact area S cc only. The variation of the weak form from (43) leads to

$$ {{\delta}} \varPi_{\mathrm{c}}^{\mathrm{LM}} \equiv C_{\mathrm{c}}^{\mathrm{LM}} = \int _{S_{\mathrm{cc}} } {{{\delta}} \boldsymbol{\lambda}^{\mathrm{T}} {\mathbf {d}}} \,\mathrm{d} S + \int _{S_{\mathrm{cc}} } { \boldsymbol{\lambda}^{\mathrm{T}} {{\delta}} {\mathbf {d}}} \,{\mathrm{d}} S = 0. $$
(44)

The first integral in (44) represents the fulfilment of the gap function d choosing an arbitrary Lagrangian multiplier vector λ. The second integral represents the fulfilment of the reaction forces for an arbitrary chosen gap function d. In case of contact the gap between the two contacting bodies is closed, and the gap function d can be replaced by the displacements of the mortar body m u m and of the non-mortar body m u nm, and the initial gap \({}^{m}{\mathbf {d}}^{m}_{0}\),

(45)

The upper left index m denotes that the displacement vectors are expressed with respect to the body-fixed mortar reference frame \(\mathcal{K}_{m}\). Additionally, the Lagrangian multiplier λ in the second integral can be replaced by the sum of the tractions of the mortar body m t m and of the non-mortar body m t nm. Hence, the equilibrium in the contact area is fulfilled by an integral meaning only.

The Lagrangian multipliers λ and their variations δ λ can be discretised in the same way as it was done for displacements and tractions. This leads to

$$ \boldsymbol{\lambda}(\xi,\eta) = \sum_i {M_i^{\lambda} } (\xi,\eta) \boldsymbol{\lambda}_i, \qquad{{\delta}} \boldsymbol{\lambda} (\xi,\eta) = \sum_i {M_i^{\lambda}} (\xi,\eta) {{\delta}} \boldsymbol{\lambda}_i, $$
(46)

where \({M_{i}^{\lambda}} (\xi,\eta)\) represents the general shape functions over one element e and λ i and δ λ i the corresponding nodal values. The same procedure can be applied to the gap function d and the corresponding variation δ d,

$$ {\mathbf {d}}(\xi,\eta) = \sum_i {M_i^{d}} (\xi,\eta) {\mathbf {d}}_i, \qquad{{\delta}} {\mathbf {d}}(\xi,\eta) = \displaystyle\sum_i {M_i^{d} } (\xi,\eta) {{\delta}} {\mathbf {d}}_i. $$
(47)

Inserting (46) and (47) into (45) leads to the constraint equations for one pair of contact elements,

(48)

The nodal values \({}^{m}{\mathbf {u}}_{j}^{nm}\) and \({}^{m}{\mathbf {t}}_{j}^{nm}\) for the degrees of freedom on the non-mortar side are given with respect to the body-fixed reference frame \(\mathcal{K}_{m}\), see (48). Typically the system matrices H nm and G nm are calculated with respect to the body-fixed reference frame \(\mathcal {K}_{nm}\). The corresponding displacements and tractions are also given with respect to \(\mathcal{K}_{nm}\). An additional transformation for the current orientation between \(\mathcal{K}_{m}\) and \(\mathcal{K}_{nm}\) is introduced so that

$$ {}^m{\mathbf {u}}_i^{nm} = {}^{m\,nm}{\mathbf {T}} \, {}^{nm}{\mathbf {u}}_i^{nm} \quad\mbox{and} \quad{}^m{\mathbf {t}}_i^{nm} = {}^{m\,nm}{\mathbf {T}} \, {}^{nm}{\mathbf {t}}_i^{nm}, $$
(49)

where m nm T is the transformation matrix between body-fixed reference frames on mortar body m and the non-mortar body nm. If (48) vanishes, the constraints for displacements and tractions are fulfilled. Considering (49) and using the fact that (48) vanishes for arbitrary variations of the Lagrangian multipliers δ λ and gap functions δ d, the contact constraints for one pair of contact elements become

$$ \begin{aligned}[c] & \int _{S_{e\mathrm{cc}} } \biggl( \sum _j {M_i^{\lambda} ( \xi_{nm},\eta_{nm})N_j } (\xi_{nm}, \eta_{nm}){}^{m\, nm}{\mathbf {T}} {}^{nm}{ \mathbf {u}}_j^{nm} \\ &\quad{} - \sum _j {M_i^{\lambda} (\xi_m,\eta_m)N_j } (\xi_m, \eta_m){}^m{\mathbf {u}}_j^m \\ &\quad{} - \sum _j {M_i^{\lambda} (\xi_m,\eta_m)N_j } (\xi_m, \eta_m){}^m{\mathbf {d}}_{0j}^m \biggr) \,{\mathrm{d}} S = {\mathbf {0}}, \\ & \int _{S_{e\mathrm{cc}} } \biggl( \sum _j {M_i^{d} (\xi_{nm}, \eta_{nm})N_j } (\xi_{nm},\eta_{nm}){}^{m\,nm}{ \mathbf {T}} {}^{nm}{\mathbf {t}}_j^{nm} \\ & \quad{} + \sum _j {M_i^{d} (\xi_m,\eta_m)N_j } (\xi_m, \eta_m){}^m{\mathbf {t}}_j^m \biggr) { \mathrm{d}} S = {\mathbf {0}}. \end{aligned} $$
(50)

For a pair of bilinear elements, the first equation of (50) results for the displacements on the non-mortar side to the matrix

$$ \scriptsize{ {\mathbf {M}}_u^{nm\,e} = \left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} {\int_{S_{e\mathrm{cc}} } {M_1^{\lambda} N_1\, {\mathrm{d}} S{}^{m\, nm}{\mathbf {T}}} } & {\int_{S_{e\mathrm{cc}} } {M_1^{\lambda} N_2\, {\mathrm {d}} S{}^{m\,nm}{\mathbf {T}}} } & {\int_{S_{e\mathrm{cc}} } {M_1^{\lambda} N_3\, {\mathrm{d}} S{}^{m\,nm}{\mathbf {T}}} } & {\int_{S_{e\mathrm{cc}} } {M_1^{\lambda} N_4\, {\mathrm{d}} S{}^{m\,nm}{\mathbf {T}}} } \\ [3pt] {\int_{S_{e\mathrm{cc}} } {M_2^{\lambda} N_1\, {\mathrm{d}} S{}^{m\, nm}{\mathbf {T}}} } & {\int_{S_{e\mathrm{cc}} } {M_2^{\lambda} N_2\, {\mathrm{d}} S{}^{m\,nm}{\mathbf {T}}} } & {\int_{S_{e\mathrm{cc}} } {M_2^{\lambda} N_3\, {\mathrm{d}} S{}^{m\,nm}{\mathbf {T}}} } & {\int_{S_{e\mathrm{cc}} } {M_2^{\lambda} N_4\, {\mathrm{d}} S{}^{m\,nm}{\mathbf {T}}} } \\ [3pt] {\int_{S_{e\mathrm{cc}} } {M_3^{\lambda} N_1\, {\mathrm{d}} S{}^{m\, nm}{\mathbf {T}}} } & {\int_{S_{e\mathrm{cc}} } {M_3^{\lambda} N_2 \, {\mathrm {d}} S{}^{m\,nm}{\mathbf {T}}} } & {\int_{S_{e\mathrm{cc}} } {M_3^{\lambda} N_3 \,{\mathrm{d}} S{}^{m\,nm}{\mathbf {T}}} } & {\int_{S_{e\mathrm{cc}} } {M_3^{\lambda} N_4\, {\mathrm{d}} S{}^{m\,nm}{\mathbf {T}}} } \\ [3pt] {\int_{S_{e\mathrm{cc}} } {M_4^{\lambda} N_1\, {\mathrm{d}} S{}^{m\, nm}{\mathbf {T}}} } & {\int_{S_{e\mathrm{cc}} } {M_4^{\lambda} N_2\, {\mathrm {d}} S{}^{m\,nm}{\mathbf {T}}} } & {\int_{S_{e\mathrm{cc}} } {M_4^{\lambda} N_3\, {\mathrm{d}} S{}^{m\,nm}{\mathbf {T}}} } & {\int_{S_{e\mathrm{cc}} } {M_4^{\lambda} N_4\, {\mathrm{d}} S{}^{m\,nm}{\mathbf {T}}} } \end{array} \right ] } $$
(51)

and for the displacements on the mortar side to the matrix

$$ \scriptsize{ {\mathbf {M}}_u^{m\,e} = \left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} {\int_{S_{e\mathrm{cc}} } {M_1^{\lambda} N_1\, {\mathrm{d}} S{\mathbf {E}}} } & {\int_{S_{e\mathrm{cc}} } {M_1^{\lambda} N_2\, {\mathrm{d}} S{\mathbf {E}}} } & {\int_{S_{e\mathrm{cc}} } {M_1^{\lambda} N_3\, {\mathrm{d}} S{\mathbf {E}}} } & {\int_{S_{e\mathrm{cc}} } {M_1^{\lambda} N_4\, {\mathrm{d}} S{\mathbf {E}}} } \\[3pt] {\int_{S_{e\mathrm{cc}} } {M_2^{\lambda} N_1\, {\mathrm{d}} S{\mathbf {E}}} } & {\int_{S_{e\mathrm{cc}} } {M_2^{\lambda} N_2\, {\mathrm{d}} S{\mathbf {E}}} } & {\int_{S_{e\mathrm{cc}} } {M_2^{\lambda} N_3\, {\mathrm{d}} S{\mathbf {E}}} } & {\int_{S_{e\mathrm{cc}} } {M_2^{\lambda} N_4\, {\mathrm{d}} S{\mathbf {E}}} } \\[3pt] {\int_{S_{e\mathrm{cc}} } {M_3^{\lambda} N_1\, {\mathrm{d}} S{\mathbf {E}}} } & {\int_{S_{e\mathrm{cc}} } {M_3^{\lambda} N_2\, {\mathrm{d}} S{\mathbf {E}}} } & {\int_{S_{e\mathrm{cc}} } {M_3^{\lambda} N_3\, {\mathrm{d}} S{\mathbf {E}}} } & {\int_{S_{e\mathrm{cc}} } {M_3^{\lambda} N_4\, {\mathrm{d}} S{\mathbf {E}}} } \\[3pt] {\int_{S_{e\mathrm{cc}} } {M_4^{\lambda} N_1\, {\mathrm{d}} S{\mathbf {E}}} } & {\int_{S_{e\mathrm{cc}} } {M_4^{\lambda} N_2\, {\mathrm{d}} S{\mathbf {E}}} } & {\int_{S_{e\mathrm{cc}} } {M_4^{\lambda} N_3\, {\mathrm{d}} S{\mathbf {E}}} } & {\int_{S_{e\mathrm{cc}} } {M_4^{\lambda} N_4\, {\mathrm{d}} S{\mathbf {E}}} } \end{array} \right ]} $$
(52)

with the 3×3 identity matrix E. The compatibility matrices for the tractions \({\mathbf {M}}_{t}^{m\,e}\) and \({\mathbf {M}}_{t}^{nm\,e}\) are created with the same procedure. Assembling the matrices of all element pairs which are possibly in contact leads to

$$ \begin{array}[c]{l@{\qquad}l} \mathbf {M}_u^m = \displaystyle{\bigcup_e} {\mathbf {M}}_u^{m\,e}, & \mathbf {M}_u^{nm} = \displaystyle{\bigcup_e} {\mathbf {M}}_u^{nm\,e}, \\ \noalign{\vspace*{3pt}} \mathbf {M}_t^m = \displaystyle{\bigcup_e} {\mathbf {M}}_t^{m\,e}, & \mathbf {M}_t^{nm} = \displaystyle{\bigcup_e} {\mathbf {M}}_t^{nm\,e}. \end{array} $$
(53)

Concluding some remarks on the shape functions M i (ξ,η) used for the interpolation of the gap d and the Lagrangian multipliers λ are given. According to [18, 37, 39], the shape functions \(M_{i}^{\lambda }\) for the interpolation of the Lagrangian multipliers λ in (46) and \(M_{i}^{d}\) for the interpolation of gap d according to (47) have to fulfil the Babuška-Brezzi or inf-sup condition. A detailed description on that topic is provided by [9]. This condition ensures a unique solution and the maximum rank of the mortar matrices \(\mathbf {M}_{u}^{nm}\) and \(\mathbf {M}_{t}^{m}\). To realise this condition, the function space of the shape functions \({M_{i}^{\lambda} }\) and \({M_{i}^{d} }\) has to be sufficiently rich. Many research work has been done to obtain an optimal set of shape functions used for interpolation of Lagrangian multipliers for domain decomposition within finite element calculations, see [36]. A dual Lagrangian multiplier formulation was proposed by [36] which leads to diagonal mortar matrices. In the present work the original approach as described by [6] is implemented. The same interpolation functions are used for the approximation of the Lagrangian multiplier λ and the gap function d within the contact area as used for the interpolation of the displacements u and the tractions t. The use of that shape functions typically ensures the fulfilment of the Babuška-Brezzi conditions. For two-dimensional contact problems, the interpolation functions are schematically shown in Fig. 4.

Fig. 4
figure 5

Approximation of the Lagrangian multiplier λ and the gap function d within the contact area. a Without boundary conditions. b With Dirichlet boundary conditions

Full size image

For the interpolation of the Lagrangian multipliers λ the mesh on the non-mortar side is used, where for the interpolation of the gap function d the mesh on the mortar side is used, as presented by \(M_{i}^{\lambda}\) and \(M_{i}^{d}\) in Fig. 4. Due to that formulation, a construction of an intermediate mesh as described by [34] is not necessary. Nevertheless to obtain mortar matrices with a maximum rank, the shape functions have to fulfil the Babuška-Brezzi condition, which leads according to [34] to the simple requirement

$$ \min\bigl( N^m, N^{nm} \bigr) \leq N^{\lambda}, N^{d} \leq\max\bigl( N^m, N^{nm} \bigr), $$
(54)

where N m and N nm represent the number of contact nodes of the mortar and non-mortar body, respectively. The corresponding numbers of nodes for the interpolation of the Lagrangian multiplier and the gap function d are given by N λ and N d. Due to the facts that the Lagrangian multipliers are approximated using the potential contacting elements on the non-mortar side and the gap function is approximated using contacting elements on the mortar side, the requirement (54) is always fulfilled if no boundary conditions are applied at the boundary of the contact area. If Dirichlet boundary conditions at the boundary of the contact area are applied, the shape functions \(M_{i}^{\lambda}\) and \(M_{i}^{d}\) at the boundary have to be modified, see Fig. 4b. According to [18, 34], the shape functions are kept constant to ensure the maximum rank of \(\mathbf {M}_{u}^{nm}\) and \(\mathbf {M}_{t}^{m}\).

6 Numerical Implementation of Mortar Matrices

First, a mortar layer is introduced between the mortar and non-mortar side, see Fig. 5.

Fig. 5
figure 6

Introduction of a mortar layer

Full size image

The mortar layer can either be located as an intermediate surface between the mortar and the non-mortar surface as presented by [27, 28, 31], or one of the contacting surfaces can be chosen as shown in [25, 36]. According to [30], the numerical integration scheme is shown in Fig. 6 and in Algorithm 2.

Fig. 6
figure 7

Integration scheme for 3D mortar elements. a Projections of the element facets onto the mortar layer. b Common area of the projected facets. c Centre of area S. d Division of the polygon into triangles. e Locating Gauss-Radau integration points on the triangles

Full size image
Algorithm 2
figure 8

Build-up of mortar matrices

Full size image

First, the element facets are projected onto the common mortar layer, see Fig. 6a. Therefore, only the corner nodes are taken into account. For bilinear elements, this consideration is sufficient because two-dimensional bilinear elements consist of four nodes only, but in case of biquadratic elements where the edges could be curved errors may occur. For simplification and an easier handle of the projected elements, this error is neglected. This approach is valid if the differences between the geometry of the biquadratic element and the corresponding 4-node element facet are not too large.

In a second step, the common area due to the overlap of the projected elements is determined, see Fig. 6b. Therefore, a modified version of the Sutherland-Hodgman polygon clipping algorithm is used as presented in [16]. The algorithm described in [16] is valid for an axis parallel clipping only. The algorithm modifications presented here are valid for clipping with arbitrary 4-point polygons as presented in Fig. 7a.

Fig. 7
figure 9

Scheme of clipping algorithm. a Clipping with 4-point polygons. b Projection of an edge point P onto the normal of the clipping edge

Full size image

The principle of the algorithm is to clip the parts outside of one polygon with respect to another one. This is done by dividing one of the elements into four clipping edges represented by the four projected edges of the element facet. According to Fig. 7a, the element 1234 is chosen to be the clipping element. The element 1′2′3′4′ is clipped with respect to the element 1234. Therefore, a flow direction according to the arrow in Fig. 7a is chosen. In case of the chosen direction the area of the element 1′2′3′4′ located on the right side of the clipping edges is cut off, because they are outside the element 1234. To create new corner points of the overlap polygon, the edges of the element 1′2′3′4′ are cut off with respect to the clipping edges.

A calculation whether one point is lying inside or outside with respect to the clipping edge is necessary. According to Fig. 7b, this is done by a perpendicular projection of the point with respect to the clipping edge. The distance vector r 12 of the two points of the clipping edge and the corresponding normal vector n 12 are given by

$$ \mathbf {r}_{12} = \left [ \begin{array}{c} x_2 - x_1 \\ y_2 - y_1 \end{array} \right ] \quad\mbox{and} \quad \mathbf {n}_{12} = \left [ \begin{array}{c} y_2 - y_1 \\ x_1 - x_2 \end{array} \right ]. $$
(55)

The resulting clipping test is given by

$$ \mathbf {n}_{12}^{\mathrm{T}} \left [ \begin{array}{c} x_P - x_1 \\ y_P - y_1 \end{array} \right ] \left\{ \begin{array}{l} > 0 \rightarrow\mathit{outside} \\ \leq0 \rightarrow\mathit{inside}. \end{array} \right. $$
(56)

The other parts of the algorithm remain unchanged, compare to [16]. Thereafter the centre of the area S of the resulting polygon, see Fig. 6c, is calculated by the arithmetic middle of the corner coordinates of the polygon. This results in a division of the polygon into triangles according to Fig. 6d. In the next step the Gauss-Radau integration points can be determined for each of the triangles according to [11, 14]. In [30] a thirteen point Gauss-Radau rule is recommended, see Fig. 8, to overcome the problem that warped meshes can not be integrated exactly.

Fig. 8
figure 10

Gauss-Radau integration points for triangles

Full size image

In contrast to typical numerical integration, not the local but the absolute coordinates are necessary. These coordinates are projected back on the mortar and the non-mortar elements, respectively. As a result, the local coordinates ξ m ,η m and ξ nm ,η nm will be obtained. The integrals over one triangle from (51) can be expressed by

$$ \int _{S_{et}} M_i(\xi_k, \eta_k) N_j(\xi_k,\eta_k)\, { \mathrm{d}} S = \sum _{l=1}^{n_g} M_i(\xi_{kl},\eta_{kl}) N_j( \xi_{kl},\eta_{kl}) W_l, $$
(57)

where S et is the surface of a triangle t of the element e while k represents the projection on the mortar m and non-mortar side nm, respectively. The variable n g represents the number of integration points and W l the corresponding weighting factors. The integral over the element surface S ecc can be evaluated by

$$ \int _{S_{e\mathrm{cc}}} M_i(\xi_k, \eta_k) N_j(\xi_k,\eta_k)\, { \mathrm{d}} S = \sum _{t=1}^{n_t} \int _{S_{et}} M_i(\xi_k,\eta_k) N_j(\xi_k,\eta_k)\, {\mathrm{d}} S, $$
(58)

which represents the sum over all triangles. Finally, the integrals can be assembled according to (53).

7 From Contact Tractions to Applied Forces

If the contact calculation inside the boundary element environment has converged, the tractions and displacements within the contact area are given. However, within the multibody environment only forces and torques can be treated. Therefore, the contact tractions t j have to be integrated with respect to the contact area to form the resulting wrench, consisting of the force \(\mathbf {f}_{T}^{\, \mathrm {\mathrm{cc}}}\) and torque \(\mathbf {f}_{R}^{\, \mathrm{\mathrm{cc}}}\), see Fig. 9.

Fig. 9
figure 11

From contact tractions to resulting wrench

Full size image

According to Fig. 9, the contact tractions have to be integrated for each contacting body with respect to the body-fixed reference frame \(\mathcal{K}_{i}\). The upper right index i denotes the mortar body m and non-mortar body nm, respectively. The body-fixed reference frame \(\mathcal{K}_{i}\) within the boundary element system is equal to the force application point within the multibody system. The resulting contact force \({\mathbf {f}}_{T}^{\, \mathrm{\mathrm{cc}}} \) can be calculated by

$$ {\mathbf {f}}_T^{\, \mathrm{\mathrm{cc}}} = \sum _e^{n_{\mathrm{c}} } \biggl[ \sum _k \int _{S_{e} } {N_k { \mathbf {t}}_k }\, {\mathrm{d}} \tilde{S} \biggr], $$
(59)

where t i represents the surface traction vector of the ith node, N i the corresponding shape functions, and S e the element surface. The integral in (59) has to be evaluated over all n c contacting elements. The resulting contact torque \({\mathbf {f}}_{R}^{\, \mathrm{\mathrm{cc}}}\) built up by the tractions t i can be calculated by

$$ {\mathbf {f}}_R^{\, \mathrm{\mathrm{cc}}} = \sum _e^{n_{\mathrm{c}}} \biggl[ {\sum _k {\sum _l { \int _{S_{e}} {{{\tilde{x}}}_{kl} N_l {\mathbf {t}}_l }\, {\mathrm{d}} \tilde{S}} } } \biggr], $$
(60)

where \({{\tilde{x}}}_{kl}\) are the components of the skew symmetric matrix representing the location of a point on the surface S e with respect to the body-fixed reference frame \(\mathcal{K}_{i}\). The integrals can be evaluated using standard Gauss integration. The overall contact wrench \({{\mathbf {\hat{f}}}}^{\, \mathrm{\mathrm {cc}}}\) from (11) is obtained by assembling the calculated contact force \({{\mathbf {f}}}_{T}^{\, \mathrm{\mathrm{cc}}} \) and torque \({\mathbf {f}}_{R}^{\, \mathrm{\mathrm{cc}}}\).

8 Dynamic Simulation of Two Contacting Spheres

To test the functionality of the algorithm, a simple multibody model is considered. A schematic representation of the dynamic model is given in Fig. 10a.

Fig. 10
figure 12

Model for dynamic simulation of two spheres. a Schematic representation. b Multibody model

Full size image

The one-dimensional model consists of two identical spheres, where the lower sphere is fixed at its lower side. The upper sphere is suspended at its upper side by a spring-damper element in vertical direction. The properties of the spring-damper element are defined by the stiffness coefficient k spring and the damping coefficient b damper. Because of the gravity g grav, the upper sphere moves downwards until the initial gap d 0 is closed. Then elastic contact between both spheres based on the elastic behaviour of both curves occurs. The multibody model consists of two rigid spheres, see Fig. 10b. The multibody data of the spheres such as mass are calculated by the density ρ and the diameter d sph. The calculation of the contact forces depends mainly on the motion of the reference frames of the spheres, which are located at the centres of the spheres. The data of the model are summarised in Table 1.

Table 1 Properties of the dynamic model
Full size table

For comparison, a reference model with existing force elements of the multibody program SIMPACK™ was created. Here, the force element containing the developed BEM contact model is replaced by a Hertzian pressure element. Here, the bodies remain undeformed and body forces are also not considered in the reference model. The transition between no contact and contact is realised by an event function. The event function depends on the relative position and on the geometry of the contacting bodies. If the gap between the spheres is closed, the integrator is stopped and restarted with new initial conditions. The Sodarst2 integrator from the multibody program SIMPACK™ is chosen. This integrator is based on an implicit formulation with automatic step size calculation.

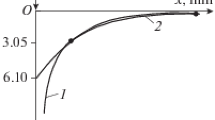
The co-simulation is done by the use of the explicit Euler integrator. The constant step size is equal to 0.0002 s. This step size is chosen to overcome the impact problem of both spheres. The simulation time is 1 s. In contrast to the reference model, the body forces are considered. The contact gap of both simulations is shown in Fig. 11.

Fig. 11
figure 13

Contact gap vs. time for BEM co-simulation and Hertzian pressure element

Full size image

The two curves agree well. Only small differences can be denoted at the end of the simulation time. The corresponding relative contact velocity of the upper contact point with respect to the lower contact point is shown in Fig. 12.

Fig. 12
figure 14

Contact velocity vs. time for BEM co-simulation and Hertzian pressure element

Full size image

Herein also small differences between the two curves can be noticed at the end of the simulation time. The contact forces of both simulations are shown in Fig. 13.

Fig. 13
figure 15

Contact force vs. time. a BEM co-simulation. b Hertzian pressure element

Full size image

The peaks of the two contact force curves differ from each other. The first peak of the Hertzian reference model reaches a value of −244.942 kN. The corresponding contact force value of the BEM co-simulation is obtained with −276.003 kN, which means a difference of −12.68 % compared to the reference model. Higher pressure force are to be expected due to the consideration of body forces. Additional differences occur due to the integrators chosen. These differences can be seen at the second peak of both curves. The contact force values are obtained as −223.215 kN and −285.308 kN for the reference model and the BEM co-simulation, respectively. The second peak of the reference model is lower than the first one because of the modelled damping d damper. Additional damping occurs due to the implicit integrator. In contrast the second peak of the co-simulation is higher. This results from the explicit Euler integrator which leads to an excitation of the numerical solution.

9 Conclusions and Outlook

The present chapter introduces the modelling of elastic contacts by coupled multibody and boundary element systems. Compared to contacts modelled by impact laws, physically more accurate results can be obtained. Due to the use of boundary element systems, the contact stresses are obtained within the contact calculation.

The contact formulation is based on mortar methods, which enables the contact calculation of non-conforming meshes. A new three-dimensional contact element for boundary element systems is developed. The mortar element uses the mixed formulation of boundary element formulations. Constraints in a weak form are defined for the displacements in the contact interface. This principle is also known from mortar formulations of finite elements. Additionally, a weak equilibrium is introduced for the tractions in the contact interface. The algorithm for the iteration of contact states is based on a Dirichlet-to-Neumann algorithm. Herein, both contacting bodies are calculated serially. In the first calculation step, one of the contacting bodies represents a rigid obstacle for the other elastic one. The resulting reaction forces on the elastic body are partially transferred on the other one, which is for the second calculation step no longer rigid. As a result the obstacle is deformed and the next iteration starts. The algorithm converges if the numerical equilibrium in the contact interface is reached.

The incorporation of the multibody and boundary element program is realised by interprocess communication. Further details are described in [41]. The multibody program stops during the calculation of the contact forces by the boundary element program. Unix domain sockets are used for communication of both programs. This coupling scheme is applied because both programs works under the same operating system on the same computer. The applied communication protocol can easily be extended to network sockets. In contrast to Unix domain sockets, network sockets allow both programs working on different computers. This property is very important for the developed BEM co-simulation because the boundary element program needs more computational resources than the multibody program. The position data provided by the multibody program are used by the boundary element program to calculate the displacements and tractions on the contacting bodies. The resulting contact tractions are summarised to a contact wrench by numerical integration.

Altogether the MBS-BEM co-simulation is an appropriate way for contact calculation in multibody systems. The main advantage is that contact stresses are obtained within the dynamic calculation. These data can be used for strength, fatigue and durability analyses. Despite to the fact that the calculation of complex models needs a large calculation time the coupled simulation of multibody and boundary element systems offers various applications.

As an application for the BEM contact algorithm, the femoral-patellar joint with sliding contact between a human patella and a femur bone is under investigation. First tests show a good convergence of the BEM contact algorithm, see Fig. 14.

Fig. 14
figure 16

Simulation of a patellar joint (in cooperation with Department of Orthopaedics, University Medicine, Rostock)

Full size image

A future task should be the speed-up of the co-simulation. The main advantage of the developed BEM contact algorithm is the possibility to integrate fast boundary element methods, because the two contacting bodies are treated separately. Fast boundary methods are developed to overcome large calculation times caused by fully populated system matrices. The panel clustering method described in [19] approximates the matrix-vector multiplication so that instead of a system matrix A of the size n×n only two vectors of the size n are calculated. Thus, the memory requirements are strongly reduced. The build-up of a binary tree or octree for the boundary elements is necessary, so that the collision detection algorithms described in [40, 41] can be used. The panel clustering method is extended to three-dimensional elastostatics in [20, 21] where the integral free term c ij from (23) is assumed to be equal to \(\frac{1}{2} {{\delta}}_{ij}\). From theoretical background this is valid for flat surfaces only, which is not typical for physical shapes in mechanical engineering. Therefore, these algorithms have to be checked carefully. Panel clustering uses hierarchical matrices which are explained in detail by [7]. First implementations of the panel clustering method for temperature distribution problems is shown in [22].

In the present contribution, quasistatic boundary element formulations are considered only. To take local vibrations and wave propagation of the elastic bodies into account dynamic co-simulation is recommended. A possible implementation is the dual reciprocity method described in [8]. The result of that method are dynamic system matrices, whereby also a system matrix in analogy to the mass matrix of finite element systems is obtained. The coupling of multibody and boundary element systems based on dual reciprocity methods to model flexible bodies is described by [3].

The integration of dynamic boundary element formulations leads to better results for elastic impact problems because the energy loss due to wave propagation is taken into account. The system matrices for that formulation are fully populated and not necessarily positive definite so that complex eigenfrequencies are obtained. To overcome these problem internal nodes are included to represent the mass distribution. In [23] it is shown that lower eigenfrequencies become real if a sufficient number of internal nodes is used. For dynamic co-simulation a separate integrator has to be implemented within the boundary element formulation. In addition other coupling schemes have to be implemented because the two simulations have to be synchronised. Special coupling schemes for co-simulation of multibody and finite element systems are described in [10] which are also applicable for the co-simulation of multibody and boundary element systems.