Evolution of Asymmetric Damage Segregation : A Modelling Approach

Abstract

Mother cell-specific ageing is a well-known phenomenon in budding yeast Saccharomyces cerevisiae. Asymmetric segregation of damage and its accumulation in the mother cell has been proposed as one important mechanism. There are, however, unicellular organisms such as the fission yeast Schizosaccharomyces pombe, which replicates with almost no asymmetry of segregation of damage and the pathogenic yeast Candida albicans, which falls around the middle of the segregation spectrum far from both complete symmetry and complete asymmetry . The ultimate evolutionary cause that determines the way damage segregates in a given organism is not known. Here we develop a mathematical model to examine the selective forces that drive the evolution of asymmetry and discover the conditions in which symmetry is the optimal strategy. Three main processes are included in the model: protein synthesis (growth), protein damage , and degradation of damage . We consider, for the first time, the costs to the cell that might accompany the evolution of asymmetry and incorporate them into the model along with known trade-offs between reproductive and maintenance investments and their energy requirements. The model provides insight into the relationship between ecology and cellular trade-off physiology in the context of unicellular ageing , and applications of the model may extend to multicellular organisms.

Introduction

The ability of all forms of life, from simple unicellular organisms to complex eukaryotes, to continue to survive is closely linked to their ability to detect errors that occur in their macromolecules and then repair them. From an evolutionary perspective, the primary function of the maintenance systems is to provide a sound internal state as the organism grows and reproduces. The external environment, however, is not under control of the organism. Indeed, the environment is typically highly variable, harsh and stressful. One inevitable product of such environments for the organism is cellular damage which, if not properly countered, threatens the survival of the lineage in unicellular forms of life and the integrity of tissues in multicellular organisms. Unrepaired genetic damage is particularly dangerous because of its direct flow to future generations. Non-genetic damage (e.g. protein damage ) is important too. When a cell divides at mitosis, all of its cytoplasmic materials, including damaged macromolecules are distributed during cytokinesis between the two daughter cells. Depending on its reparability, all or parts of damage may be further transferred to the next generation.

How can a cell deal with damage and maximise its Darwinian fitness in environments with various sources of stress? Irreversible protein damage is a serious problem because the multitude of costly repair mechanisms that exist in the cell is of no use in this regard. The way this damage is inherited by the daughter cells is also important. Maximal dilution occurs with symmetric distribution of damage at division. In order to be effective, symmetry needs to be accompanied by sufficiently rapid proliferation (Rashidi 2008). Otherwise, both daughter cells (i.e. the lineage) would suffer the same risk of accumulated damage rising eventually to a lethal level. Thus, symmetry is expected to be an efficient strategy to cope with irreversible damage when the environment is not too harsh, the cell is sufficiently rich in repair mechanisms, and/or proliferation is sufficiently fast. The advantage of making do with symmetry is that it does not require a separate and potentially costly mechanism to evolve. The disadvantage concerns the requirement for sufficient investment in maintenance (i.e. efficient repair) and/or reproduction (i.e. rapid proliferation). As an example, damage inheritance in the unicellular fission yeast Schizosaccharomyces pombe (S. pombe) is strikingly symmetric. The “old” daughter cell in this organism receives on average only 55% of maternal carbonylated proteins (Minois et al. 2006).

In contrast, asymmetric segregation of damage favours the survival of a lineage by specifically promoting the survival of the daughter cell that inherits less damage . Sufficient asymmetry (one daughter cell is born with no damage in the extreme case) may guarantee lineage survival and compensate for slow reproduction and/or inefficient maintenance systems. Not surprisingly, asymmetric inheritance is prevalent in all kingdoms of life, from yeast to higher eukaryotes (Aguilaniu et al. 2003; Macara and Mili 2008; Rujano et al. 2006). The main issue with asymmetry is a potential need for specific mechanisms including new genes, molecules or interactions to evolve. It is not trivial to see what proportion of resources the cell is best to invest in maintenance, reproduction, and possibly asymmetry when resources are limited. Resource limitation causes a multitude of trade-offs at different levels (subcellular, cellular, organismal) to emerge (Fischer et al. 2009; Stearns 1976). Mathematical modelling is an alternative to the classical experimental approach in the study of these trade-offs. Here we investigate and model the evolution of non-genetic damage segregation in unicellular organisms.

The Model

Basic Assumptions

The model is based on a single haploid asexual cell which founds a genetically homogenous colony. Regarding damage accumulation and degradation, we study 3 genes, each with one quantitatively indentified locus. The quantitative value (s, Δ, g) of the genes (e.g. corresponding to their expression level) determines the strength of the particular traits they produce. The traits are protein synthesis rate, protein damage rate, and protein damage degradation rate, respectively. Since colonies are assumed genetically homogenous, we ignore rare mutations that might occur to the three genes of our interest. We are interested in damage only to the non-genetic materials inside the cell (e.g. proteins) and only irreversible types of damage (e.g. protein carbonylation (Stadtman 2006)). Proteins are synthesised at a constant rate s. A constant proportion of the existing proteins are assumed to become irreversibly damaged at rate Δ. While repair is the principal way by which cells handle reversible forms of damage , there are generally three ways to cope with irreversible damage : (i) degradation (e.g. by the ubiquitin/proteasome system), (ii) exocytosis, and (iii) simply living with damage . With the latter, and if the cell survives to reproduce, damage may be diluted between the two daughter cells such that each inherits only part of the damage . The proportion of damage received by each daughter cell affects their chances for survival and thus their fitness (Ackermann et al. 2007; Evans and Steinsaltz 2007; Fredriksson and Nyström 2006; Watve et al. 2006). This proportion may also influence the survival of the colony (Erjavec et al. 2008). For example, with sufficient asymmetry in segregation of damage , the daughter cells in each generation which are born with relatively little damage can guarantee the survival of the lineage. The level of segregation asymmetry is assumed to be a heritable trait and rare mutations are not considered. We combine strategies (i) and (ii), collectively referred to as “degradation”. Reproduction takes place by cell division during which damaged particles in the mother cell are distributed between the two daughter cells. The timing of cell division depends on the amount of undamaged materials (in this model, native proteins) in the cell (Erjavec et al. 2008). When the number of native protein molecules reaches a certain threshold, the cell divides. If damage (D) increases beyond a fixed threshold D ^*, the cell dies. Death occurs by an apoptosis-like process and does not affect neighbouring cells.

Fitness (of a cell) is defined as the number of descendants it produces per unit of time. The unit of time is arbitrary (as long as it is constant for comparison purposes) and can be defined large enough for cells to reproduce. We assume that the most primitive unicellular organisms had more symmetric damage segregation strategies than the more recently evolved cells. Therefore, the default strategy is assumed to be symmetric and we try to find triplets of the form (s, Δ, g) for which asymmetry pays. As a specific case, if all members of a colony that segregate damage symmetrically and descend from a given triplet survive, asymmetry will be associated with no fitness advantage and will thus not evolve. We develop the model in three successive steps. First, we assume that degradation mechanisms have not yet evolved. Next, we relax this assumption. In these two steps, the cell does not have to pay any costs (metabolic, energetic) to evolve asymmetry . In the third step, asymmetry is associated with a fixed cost detracted from resources invested in maintenance and/or reproduction.

Structure of the Model

There are 3 continuous-time processes (protein synthesis, protein damage accumulation, and damage degradation) and 3 instantaneous events (cell division, damage segregation , and cell death) in the model. The continuous-time processes are embedded in and modelled as the following 2 ordinary differential equations:

$$\begin{array}{l} dp/dt = s - \Delta p \\ dD/dt = \Delta p - gD \\ \end{array}$$

((14.1))

Proteins (p) are synthesised at a constant rate (s) and are irreversibly damaged by a first-degree kinetic process with constant Δ. Damaged proteins (D) are also degraded by the same kind of process with constant g. The cell divides when normal proteins reach a threshold p ^* unless damage has already reached a threshold D ^* in which case the cell dies before division. Without loss of generality, we let p ^* = 1. Time (t) is measured from the time the cell is born. In order to give our cells a chance to reproduce, we assume s > Δ. Without this assumption, the cell dies before it can divide. Segregation of damage at division is assumed to occur according to a segregation coefficient σ, which is a heritable trait. A proportion σ of damage segregates to one of the daughter cells and the rest of the damage goes to the other cell. To set the initial conditions, we note that D(0) is the amount of damage that a daughter cell inherits from its mother. Since aggregation of damaged proteins makes them more stable (and so makes their turn-over slower than that of normal proteins), we do not consider the inheritance of normal proteins (Carrio and Villaverde 2003; Maisonneuve et al. 2008). In other words, we let $p\left(0\right) = 0$.

Results

No Degradation

In this case, corresponding to g = 0, the degradation mechanisms have not yet evolved or are negligibly primitive. The system has no fixed points (i.e. stable or unstable steady states) and the amount of accumulated damage increases in an explosive manner. The only chance for survival is rapid reproduction such that before damage reaches fatal levels, the cell has already divided.

To examine the fate of the population and the advantages of asymmetry , let us look closely into the behaviour of the model. It can be shown that the necessary and sufficient condition for survival of a cell (until division) is

$$D\left(0\right) < 1 + D^* + \Delta ^{ - 1} sLn\left(1 - \Delta /s\right)$$

((14.2))

The accumulated damage during a cell cycle is constant:

$$x = - 1 - \Delta ^{ - 1} sLn\left(1 - \Delta /s\right)$$

and (14.2) can be rewritten as:

$$D\left(0\right) + x < D^*$$

We define d(0) to be the initial amount of damage in the founder cell. With that, three possibilities can be considered:

• (i) $x < d\left(0\right)$: In this case, and as long as the cells follow a symmetric segregation strategy, the accumulated damage at the time of cell division declines with advancing generations and there is no death in the population. Therefore, asymmetry cannot be associated with any fitness advantage in this situation.

• (ii) $d\left(0\right) < x < D^{*}/2$: In this case, and as long as the cells follow a symmetric segregation strategy, the accumulated damage at the time of cell division grows with advancing generations to $2x < D^*$. Again, symmetry offers the highest possible fitness and there is no selection pressure for asymmetry .

• (iii) $x > \max \left\{ d\left(0\right),D^* /2\right\}$: In this case, and with symmetry, the accumulated damage at the time of cell division grows with advancing generations to $2x > D^*$. If the younger daughter cells receive more than a proportion max$\{\left(D^* - x\right)/D^* ,d\left(0\right)/\left(d\left(0\right) + x\right)\}$ of maternal damage , the population will disappear at some point. Sufficient asymmetry enhances fitness and prevents the population from vanishing.

With Degradation

Now we evaluate the case where cells already possess degradation mechanisms and hence g > 0. The cell cycle duration and total damage accumulated in the cell at time of division, if the accumulated damage is not high enough to have already killed the cell are given by

$$\begin{array}{l} T = - \Delta ^{ - 1} Ln\left(1 - \Delta /s\right) \\ D_T = \Delta \left(g - s\right)/g\left(g - \Delta \right) + \left(D\left(0\right) + s/\left(g - \Delta \right) - s/g\right)\left(1 - \Delta /s\right)^{g/\Delta } \\ \end{array}$$

The analysis of the system shows that with sufficiently long cell cycle duration, the dynamics of the accumulated damage in a cell follows one of the following 3 patterns:

• (i) Damage increases to a finite maximum. This case occurs when $D\left(0\right) = 0$.

• (ii) Damage decreases to a minimum. This case occurs when $D\left(0\right) > s\Delta /g\left(\Delta - g\right) > 0$.

• (iii) There is an initial decline in damage after which damage increases to a finite maximum. This is the case for any condition that does not satisfy (i) and (ii).

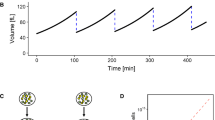
The system has one steady state$\left(p,D\right) = \left(s/\Delta ,s/g\right)$, which is stable (Fig. 14.1).

Fig. 14.1

The stable steady state of the system with three typical trajectories. All trajectories are attracted to the steady state, shown by the dashed line. a The ratio of maintenance to growth investment is sufficiently high (g/s > 1/D ^*). b The maintenance/growth ratio is low (g/s < 1/D ^*)

Symmetry offers the highest possible fitness (all cells survive) when $s < gD^*$. Also, symmetry is the best strategy (all cells survive) if both of the following two conditions hold (see Appendix for detailed analysis):

$$\begin{array}{l} gD^* < s < \Delta \left(1 + D^* \right)/4 \\ \left(\Delta - \sqrt {\Delta ^2 - 4s\Delta /\left(1 + D^* \right)} \right)\big/2 < g < \min \left\{ \Delta ,\left(\Delta + \sqrt {\Delta ^2 - 4s\Delta /\left(1 + D^* \right)} \right)\big/2\right\} \\ \end{array}$$

((14.3))

Costs of Asymmetry

In the previous two sections, we have implicitly assumed that asymmetry has no cost (in terms of available resources or energy budget of the cell) for the cell, that is, the molecules that may provide an asymmetry -generating mechanism have already evolved in the cell for other purposes and asymmetry is either a costless by-product of their existence or the costs to the cell of the new interactions that need to be created between those molecules are negligibly small. Now, we relax this simplistic assumption and analyse a case in which the total energy budget of the cell is allocated in an optimal fashion to three categories of physiological functions: maintenance (required budget: e _m ), reproduction (required budget: e _r ), and asymmetry (required budget: e _a ). There is no explicit mathematical formula to deal with this in a general way, so for tractability we only compare symmetry with complete asymmetry (σ = 1). In other words, we do not calculate the fitness conferred by partially asymmetric segregation strategies (e.g. σ = 0.8).

We make two further assumptions: (i) the rate of damage accumulation is inversely related to maintenance investments (under constant environmental conditions), and (ii) the cell cycle duration is inversely related to reproductive investments (Fig. 14.2). Let us represent these two relationships with $g\left(e_m \right)$ and $f\left(e_{r} \right)$, respectively. Therefore, the amount of damage accumulated (and added to the initial damage the cell is born with) during a cell cycle will be $g\left(e_m \right)f\left(e_r \right)$.

Fig. 14.2

Fundamental relationships stemming from physiological trade-offs. A cell invests in reproduction and maintenance. a The proliferation rate increases and thus the cell cycle duration decreases with increasing reproductive investment. The cell cycle can become infinitely long (with little investment in reproduction), but due to physicochemical constraints it cannot be shorter than a certain minimum. b The rate of damage accumulation decreases with increasing maintenance investment. The environment is assumed as a finite source of stress such that damage accumulation cannot be infinitely fast, even when maintenance investment is minimal. A minimum rate of damage accumulation is inevitable, irrespective of the level of maintenance investment

It can be shown that with a symmetric segregation strategy, every cell in the population survives to reproduce if

$$g\left(e_m \right)f\left(e_r \right) < \min \left\{ D^* /2,D^* - D\left(0\right)\right\}$$

Consequently, the highest possible fitness with symmetry is achieved by

$$e_m \left(opt\right) = \min \left\{ e_m :g\left(e_m \right)f\left(e_r \right) < \min \left\{ D^* /2,D^* - D\left(0\right)\right\} \right\}$$

Figure 14.3 and the fitness (population size at time t) associated with this optimal strategy will be

$${\textrm{fitness}}_{\textit{max}} = 2^{t/f\left(e - e_m \left(opt\right)\right)} $$

((14.4))

Fig. 14.3

The condition in which symmetry offers its highest possible fitness advantage. Maintenance investment needs to be set at the lowest value for which the amount of damage accumulated during a cell cycle is less than a certain minimum

With (complete) asymmetry , the amount of damage in a given cell increases to the time of division and then completely segregates to one of the daughter cells. As a result, one can trace the original cell through generations. When damage reaches the fatal threshold D ^*, the cell dies. Therefore, a cell lives for a certain number, l, of cycles that depend on its initial damage , the fatal damage threshold, and the amount of damage accumulated in each cell cycle. We have

$$l = \left[\left(D^* - D\left(0\right)\right)/g\left(e_m \right)f\left(e_r \right)\right],$$

where [u] is the largest integer smaller than or equal to u. For example, if the accumulating damage kills an initially damage -free cell (i.e. its old daughter cell in this example) during its second cell cycle, l will be 1 and the population size at any time (after the first cell cycle is completed) will be 2. Compared to the symmetric case discussed above, this is a considerably low fitness value. When l = 2 (i.e. damage kills a granddaughter of an initially damage -free cell), it can be shown that

$$N\left(n + 1\right) = 2\left(N\left(n\right) - N_d \left(n\right)\right),$$

((14.5))

where N(n) and N _d (n) denote the total number of living cells and the number of cells that die in generation n, respectively. Further analysis shows that N _d (n) is a Fibonacci number and hence

$$N_d \left(n\right) = \left(\phi ^{n - 1} - \left(1 - \phi \right)^{n - 1} \right)/\sqrt 5 ,$$

((14.6))

where $\varphi = \left(1 + \sqrt 5 \right)/2$. Substituting (14.6) into (14.5) and with some algebraic calculations we have

$$\begin{array}{l} N\left(n\right) = 2\left(\varphi ^{n + 1} - \left(1 - \varphi \right)^{n + 1} \right)/\sqrt 5 \\ N\left(0\right) = 1,N\left(1\right) = 2 \\ \end{array}$$

N(n) in this formula generates delayed (i.e. without the first term in the classical sequence) Fibonacci numbers. There is no general formula for l > 2. The sequences corresponding to l > 2 are Fibonacci-like sequences in which each term is the sum of its previous l terms, and the first l terms of the sequence are increasing non-negative powers of 2. The growth rate of such sequences is initially higher than that of the simple power sequence derived in (14.4), which will eventually overtake the Fibonacci-like sequences. Therefore, asymmetry pays at small carrying capacities. When asymmetry is rare, it remains rare if the carrying capacity of the population is sufficiently large. It should be emphasised that we have only considered σ = 1 as asymmetry . Our results might be different with intermediate levels of asymmetry . This is important because although there is currently no known mechanism that generates a well-regulated submaximal level of asymmetry , the fidelity of damaged macromolecules in following complete segregation asymmetry may not be complete. This imperfectness becomes particularly important when the number of independently behaving damaged molecules is small (e.g. aggregation of damaged proteins) and the infidelity of segregation is considerable. The effects of this type of stochasticity are shown in Fig. 14.4. In such conditions, a mechanism which is meant to produce complete asymmetry will actually lead to intermediate levels of asymmetry .

Fig. 14.4

The effects of particle number and segregation fidelity on damage variation. Variance of the proportion of premitotic maternal damage received by d ₁ , the daughter cell into which damaged particles segregate with a higher probability, is higher for smaller values of n (the number of independently behaving damaged particles in the mother cell immediately before mitosis) and σ, the segregation coefficient. Points located on a given curve exhibit the same level of variance in damage , represented by the number on the curve

Figure 14.5 compares symmetric cases with asymmetric ones for the relationship between e _m and fundamental properties of the system (i.e. cell cycle duration and accumulated damage per cell cycle). The costs of asymmetry are inevitably detracted from resources that could otherwise be maximally allocated to reproductive and/or maintenance functions.

Fig. 14.5

Comparison between symmetry and asymmetry for the relation between maintenance investments and fundamental properties of the system (i.e. cell cycle duration and the accumulated damage per cell cycle). With asymmetry , there are lower amounts of resources available for maintenance/reproduction investment. With asymmetry , the cell cycle duration curve is shifted to the left (a) and the damage accumulation curve is transformed and shifted to the left (b)

Discussion

General Implications of the Results

In the first section of the model, we showed that before degradation evolves, symmetry is an optimal strategy unless damage accumulation during a cell cycle is significantly high. This case is possible with small investments in reproduction, which prolong the cell cycle, and in stressful environments. If resources in such environments are low, cells will not be able to increase the energy allocated to reproduction and the damage caused by stress will accumulate during the (relatively) long cell cycle to dangerous levels. Asymmetry is the only solution in these conditions. In the second section of the model, cells had already evolved degradation mechanisms. As expected, asymmetry evolves less readily in this case. In particular, symmetry is an optimal strategy when the ratio of maintenance to growth investment is sufficiently high (i.e. g/s > 1/D ^*). When this is not true, the condition derived in (14.3) opposes the evolution of asymmetry . It should be noted that there might be other cases in which symmetry is the optimal strategy. We only derived the conditions leading to two major categories of such cases.

The third section of the model was the most general situation and considered the possibility of asymmetry being associated with certain costs. Potential costs of asymmetry have not yet been identified. Many components of the known asymmetry -generating mechanisms have other functions in the cell. For example, heat shock proteins, a large family of highly conserved and constitutively synthesised molecular chaperones, assist refolding and degradation of misfolded proteins, and may mediate the upstream part of the pathway leading to asymmetric segregation of damage (Bardwell and Craig 1984; Kültz 2003, 2005; Liang and MacRae 1997). Two well-known heat shock proteins that bind to irreversibly damaged proteins are Hsp70 (DnaK) and Hsp104 (ClpB) (Barnett et al. 2005; Erjavec et al. 2007; Hartl 1996; Mogk et al. 1999; Zimmerman et al. 2004). At least some elements required for asymmetry have therefore already evolved and hence natural selection could simply exploit them for a novel purpose without needing to pay additional costs. However, new molecular interactions might have been needed to be established and the costs associated with these inventions remain to be seen. Distal parts of the pathways that move damaged molecules (using the cytoskeleton) seem to be more specifically linked to the asymmetry mechanism. Examples of such components are certain J domain proteins (e.g. rsp1p in S. pombe and glsA in the simple multicellular organism Volvox carteri) that form a bridge between heat shock proteins and the cytoskeleton (Miller and Kirk 1999; Zimmerman et al. 2004). The costs associated with evolution of these molecules may have well been significant. It has been estimated that the average yeast protein can change its expression only by 0.5% without a change in energy costs visible to natural selection (Wagner 2005, 2007). The constraint introduced by the limited available energy budget on changes in gene expression become particularly significant at large effective population sizes, where rapid proliferation is tightly coupled to an efficient energy metabolism (Fay et al. 2004; Townsend et al. 2003). Recent studies on budding yeast Saccharomyces cerevisiae (S. cerevisiae) suggest that even single amino acid replacements (which might generate asymmetry here) can be subject to natural selection on the basis of their material costs (Bragg and Wagner 2009). We showed that the carrying capacity of the population is a critical determinant of early stages of evolution of asymmetry , i.e. when asymmetry was rare. With abundant resources in the environment, for example, we do not expect high selection pressures for evolution and spread of asymmetry when it is rare.

The condition derived for evolution of asymmetry when it is costly is not uncommon. It is reminiscent of a well-known evolutionary question on origin of life. In competition between a Malthusian replicator (capable of template-mediated self-replication) and a one-member hypercycle (capable of both template-mediated and enzyme-mediated self-replication), large carrying capacities oppose the evolution of Malthusian replicators when they are initially rare (Michod 1999).

Links to Ageing

The intrinsic biology of cellular ageing is closely linked to asymmetric damage partitioning (Ackermann et al. 2003; Johnson and Mangel 2006; Kirkwood 2005). Damage segregation in unicellular organisms is a strategy with several potential advantages including rapid growth (Evans and Steinsaltz 2007; Watve et al. 2006), improved damage handling (Ackermann et al. 2007; Fredriksson and Nyström 2006; Johnson and Mangel 2006), and more resistance against clonal senescence (Erjavec et al. 2008). Interestingly, neither symmetry nor asymmetry is universal. S. cerevisiae, Candida albicans, and S. pombe use, on average, segregation strategies σ = 0.75, σ = 0.65, and σ = 0.55, respectively (Aguilaniu et al. 2003; Fu et al. 2008; Minois et al. 2006). We have recently developed a stochastic model to account for this range (manuscript under review). Three parameters, namely d (damage accumulation rate), μ _i (damage -induced death), and m (proliferation rate), were found to be correlated to asymmetry . The simplest model which was capable of explaining more than 90% variation of the outcome of evolution was composed of d, m, and the interaction term d × μ _i . Specifically, large values of d and d × μ _i and small values of m were significant predictors of asymmetry . The model was stochastic and did not include costs of asymmetry . The following points summarise the results of the stochastic model:

• 1. The outcome of evolution depends both on organismal and ecological conditions. A significant proportion of individuals in mutation-prone populations do not follow the fitness-maximising level of asymmetry (as related to individual fitness) after the population has reached steady state distributions of segregation strategies.

• 2. High rates of damage accumulation and severe damage with sufficiently detrimental effects on survival promote the evolution of asymmetry . Mutations that promote asymmetry are particularly favoured in harsh environments.

• 3. Rapid proliferation reduces the force of selection for asymmetry .

• 4. Asymmetry might be an alternative strategy to heavy investments in maintenance functions.

Here we provided analytic proofs and considered asymmetry costs. The total energy budget available to the organism (the cell in unicellular organisms) is limited. Accordingly, the disposable soma theory of ageing is built on the trade-offs resulting from resource limitation and concerns the evolutionarily optimised balance between cellular investment in reproduction and maintenance/repair (Kirkwood and Holliday 1979). With high rates of extrinsic mortality in nature, it is not beneficial to put more resources into maintenance functions than are needed for the organism to survive to the time of reproduction. Due to this submaximal maintenance investment, the organism accumulates damage , declines in its physiological functions, and thus ages. While investment in growth, reproduction, maintenance, and repair directly affect the investor, investment in asymmetry does not. It only makes sense when one considers the investor’s related kin. The offspring and next generations, rather than the same cell, benefit from asymmetry investment. Nevertheless, the costs (if any) of asymmetry have to be paid by the same cell and from its total energy budget. Perhaps the disposable soma theory needs to be expanded to include asymmetry costs.

Transition to Multicellularity

The results of the model developed here cannot be immediately extended to multicellular organisms. One important reason concerns the definition of fitness. In unicellular forms of life, the cell is the whole organism and so the fitness of the cell is the same as the fitness of the organism. The well-being of the cell is equal to the well-being of the organism and strategies that improve cell survival and/or reproduction are selected for in these simple organisms. This is not the case in multicellular organisms. All cellular strategies have to be tuned during the course of evolution and aligned with the benefit of the organism. Cell-level selfishness in a multicellular organism leads to disruption of cooperative behaviour and pathology (e.g. cancer (Michor et al. 2003)). Cells might even be sacrificed in order for the individual to survive and reproduce, as is thought to occur when intestinal stem cells preferentially undergo apoptosis following low-dose irradiation (Potten 2004). In spite of these issues, asymmetry has found its way into all kingdoms of life. Stem cell division is one example. Damaged proteins targeted for proteasomal degradation are asymmetrically distributed during mitosis in human embryonic stem cells (Fuentealba et al. 2008). Stem cell division in adulthood is the same. Irreversibly damaged proteins in Drosophila melanogaster neuroblasts and intestinal crypts of patients with protein folding disease are asymmetrically distributed to one of the daughter cells (Rujano et al. 2006).

Damage may act as a cell fate determinant by at least two ways. Firstly, it reduces the chances for survival. Secondly, it might attract signalling molecules. The generated signal may then activate certain metabolic pathways and eventually lead to altered cellular decisions such as growth and differentiation. Has damage and its asymmetric segregation been utilised by evolution at early stages of multicellularity to promote cellular differentiation and division of labour? Is the efficiency and activity of the maintenance/repair system regulated during embryogenesis in a way that damage levels change at specific times and at specific locations within the growing embryo? How much of the difference between somatic and germ-line protection against damage (e.g. oxidative) can be explained so? These are some of the questions that should be addressed in future research.

Conclusions

We developed a simple model for evolution of asymmetric non-genetic damage segregation in unicellular organisms and investigated the conditions in which asymmetry might be a beneficial strategy to evolve. The main components of the model were protein synthesis, damage accumulation, and damage degradation. The energy requirements of growth, maintenance, and possibly asymmetry were incorporated into the model. We suggest that asymmetry is a fundamental fitness modulator and if sufficiently costly, needs to be considered as part of the trade-offs that arise as a result of resource limitation. The most obvious application of our results concerns the evolutionary origin of ageing and yeast is the best known but only one target for testing the predictions of the present model. The model may be extended to include any form of non-genetic damage . Preferential segregation and accumulation of extrachromosomal rDNA circles (ERC) in the mother cell have been proposed to contribute to yeast mother cell-specific ageing (Sinclair and Guarente 1997). One can choose to think of ERCs as damaged molecules and then use the idea of mother cell bias in asymmetric segregation (Shcheprova et al. 1998) to apply the model. Changes that occur to the asymmetry -related mechanisms at the transition to multicellularity are another interesting direction for future research.

Appendix

Here we show that with conditions introduced in equation (14.3) in the text, all cells survive under symmetry, that is to say, symmetry is the best strategy. By looking at Fig. 14.1b, we realize that the condition for survival of the cell is

$$D_T < D^*$$

Considering the equation for D _T derived in section “With Degradation”, we will have

$$D\left(0\right) < s\Delta /g\left(\Delta - g\right) + \left[D^* + \Delta \left(g - s\right)/g\left(\Delta - g\right)\right]\left[s/\left(s - \Delta \right)\right]^{g/\Delta }$$

If the right-hand side of the above equation is larger than D ^*, it can easily be seen that everybody will survive. For this to happen we need

$$\left[s\Delta /g\left(\Delta - g\right) - D^* \right]\left\{ 1 - \left[s/\left(s - \Delta \right)\right]^{g/\Delta } \right\} + \left[\Delta /\left(\Delta - g\right)\right]\left[s/\left(s - \Delta \right)\right]^{g/\Delta } > 0,$$

which then gives

$$s\Delta /g\left(\Delta - g\right) - D^* < \left[\Delta /\left(\Delta - g\right)\right]\left[s/\left(s - \Delta \right)\right]^{g/\Delta } \left\{ \left[s/\left(s - \Delta \right)\right]^{g/\Delta } - 1\right\} ^{ - 1} $$

((14.7))

The right-hand side of the above equation is larger than 1 for g < Δ. For (7) to hold, we now only require

$$s\Delta /g\left(\Delta - g\right) - D^* < 1$$

Equivalently, we need

$$g^2 - \Delta g + s\Delta /\left(1 + D^* \right) < 0$$

This requires (for the above equation to have real roots)

$$s < \Delta \left(1 + D^* \right)/4$$

((14.8))

and

$$\left(\Delta - \sqrt {\Delta ^2 - 4s\Delta /\left(1 + D^* \right)} \right)/2 < g < \left(\Delta + \sqrt {\Delta ^2 - 4s\Delta /\left(1 + D^* \right)} \right)/2$$

((14.9))

Putting (14.8) and (14.9) together with g < Δ, we have the conditions derived in (14.3). Note that these are sufficient, but not necessary, conditions.

Note

While this chapter was under review, an interesting article was published by Lindner et al. (2008). The authors demonstrated asymmetric segregation of protein aggregates between the offspring in Escherichia coli. Accumulation of the aggregates to the older pole of the cell results in a progressively ageing mother cell (i.e. old-pole progeny) and rejuvenated new-pole progeny. The authors showed that the segregation of protein aggregation is associated with significant loss of reproductive ability in the old-pole progeny compared to the new-pole progeny. Also, Klinger et al. (2010) showed in another article that the oxidatively inactivated acotinase in budding yeast is distributed between the mother cell and the daughter cell according to volume asymmetry , but the still active part of the enzyme is preferentially segregated to the daughter cell. The authors suggested that this process aids the rejuvenation of the daughter cell.