Keywords

1 Introduction

In offshore installations and deep sea marine operations, one of the most important issues is how to provide safety and high operability of payloads. This means that the payload motion should be kept unaffected by the supporting vessel motion, since waves, wind and ocean currents can easily cause an unexpected motion of the vessel, which in turn has adverse effects on the cable connecting between the payload and the vessel. The unexpected horizontal motion of the vessel is often controlled by a dynamic positioning system. To reduce the adverse effects in the vertical direction, active heave compensation systems are usually been used.

The control problems for active heave compensation systems have been addressed by numerous researchers in the past. In [1], a linear control scheme was presented for an active heave compensation system. However, the authors assumed that the vessel motion due to waves was known, which is generally hard to be accomplished in practice. To remove this restriction, the jointed problems of wave synchronization and heave compensation were studied in [2, 3]. In both works, the authors assumed that only the heave acceleration was measured and its integrals were obtained via high-pass filters. In [4], a nonlinear controller for an electro-hydraulic system driven by a double-rod cylinder was proposed, whereas the vessel motion and acting force were estimated by disturbance observers. The authors in [5] designed an autopilot for the autonomous landing of a vertical take off and landing vehicle on a ship oscillating in the vertical direction, which was based on the approach introduced in [6]. An improved work was presented in [7], where the reconstruction of the wave disturbances was accomplished by using the adaptive external models proposed in [8]. For the system with time delays in sensors and actuators, a prediction algorithm was designed in [9] to predict the vessel motion.

This chapter focuses on active heave compensation control of an electro-hydraulic system driven by a double-rod actuator. An adaptive observer is proposed to estimate the system states and the force acting on the cable. By assuming that the vessel motion can be represented by a set of harmonics with known frequencies as [10], an observer is also developed to asymptotically reconstruct these harmonic signals. These observers are then implemented in the control design procedure. The control development and stability analysis are based on the Lyapunov’s direct method and backstepping technique.

2 Problem Formulation

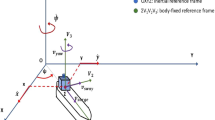
The active heave compensation system under consideration is depicted in Fig. 87.1. This system consists of an electro-hydraulic system driven by a double rod actuator, which is fixed to the vessel. The payload connects to the piston of the hydraulic system via a cable and a ball joint, where the cable is assumed rigidly. In Fig. 87.1, the reference water level is a horizontal line fixed to the earth. The heave motion of the vessel with respect to this level is denoted by z. The position of the piston with respect to the vessel is represented by \( x_{h} . \) L and d denote respectively the cable length and the desired position of the payload with respect to the reference water level.

Fig. 87.1
figure 1

Sketch of an active heave compensation system

Full size image

Following [4], the scaled model of the active heave compensation system can be written as

$$ \begin{aligned} \ddot{x}_{h} \,=\, & \theta_{1} \bar{P} - \theta_{2} \dot{x}_{h} + \theta_{3} f(t) \hfill \\ \dot{\bar{P}} \,=\, & - \theta_{4} \dot{x}_{h} - \theta_{5} \bar{P} + \theta_{6} \bar{x}_{v} \hfill \\ \dot{\bar{x}}_{v} \,=\, & - \theta_{7} \bar{x}_{v} + \theta_{8} i \hfill \\ \end{aligned} $$
(87.1)

where \( \theta_{i} (i = 1, \ldots ,8) \) are model parameters, \( \bar{P} \) and \( \bar{x}_{v} \) denote the scaled load pressure and spool displacement of the servo valve respectively, i is the control current input of the servo valve, and f(t) represents the resulting forces in the vertical direction acting on the piston. Generally, it is hard to derive the explicit expression of f(t) since it depends on too many factors. Hence, following [4], we treat it as a disturbance. On the other hand, it should be noted that only part of the states of the system (87.1) can be practically measured. To facilitate the control development, we assume that the velocity of the piston, \( \dot{x}_{h} , \) is the measured output.

In this chapter, the control objective is to make the heave velocity of the payload with respect to the reference water level, \( \dot{d}(t) \) (see Fig. 87.1), to track a desired velocity reference. On the other hand, one can see from Fig. 87.1 that

$$ d(t) = z(t) + x_{h} (t) - L $$
(87.2)

where the vessel motion z(t) can be generally decomposed into a set of harmonic oscillations and an additional slow time-varying term, i.e.,

$$ z(t) = \underbrace {{\sum\nolimits_{i = 1}^{n} {A_{i} \sin (\omega_{i} t + \phi_{i} )}}}_{w(t)} + v(t) $$
(87.3)

where \( n \ge 1,\,A_{i} ,\,\omega_{i} \,\,{\text{and}}\,\,\phi_{i} \) are the amplitude, frequency and phase of the ith mode respectively. In this chapter, we assume that the term v(t) is a constant.

Then, from (87.2) and (87.3), one can see that the control objective is equivalent to the problem of stabilizing the following heave tracking error

$$ e(t) = \dot{w}(t) + \dot{x}_{h} (t) - c(t) $$
(87.4)

where c(t) is the desired speed, and without loss of generality, we set it as a constant.

Note that (87.4) is generally not available for feedback since \( \dot{w}(t) \) is usually unknown, whereas its derivative, \( \dot{w}(t), \) is assumed to be measured via high precision accelerometers. To overcome this difficulty, we will also design an observer for w(t) in the next section. On the other hand, to facilitate the observer design procedure, the following assumptions for w(t) and f(t) are made.

Assumption 1

The frequencies of the harmonics, \( \omega_{i} (i = 1, \ldots ,n), \) are known, whereas the amplitudes and phases of the harmonics are not.

Assumption 2

The variables f(t) is globally bounded and there exists a nonnegative constant \( \sigma_{f} \) such that the first order time derivative of f(t) satisfies

$$ \left| {\dot{f}(t)} \right| \le \sigma_{f} . $$
(87.5)

Furthermore, since the heave position is left uncontrolled, the state \( x_{h} \) in (87.1) is negligible, and thus, the entire system can be reduced to a third-order system given by the following state space form

$$ \begin{aligned} \dot{x} = & Ax + Bu + Df(t) \hfill \\ y = & Cx \hfill \\ \end{aligned} $$
(87.6)

with \( x = [\dot{x}_{h} ,\bar{P},\bar{x}_{v} ]^{ \top} ,\,B = [0,0,\theta_{8} ]^{ \top } ,\,C = [1,0,0],\,D = [\theta_{3} ,0,0]^{ \top } \) and

$$ A = \left[ {\begin{array}{*{20}c} { - \theta_{2} } & {\theta_{1} } & 0 \\ { - \theta_{4} } & { - \theta_{5} } & {\theta_{6} } \\ 0 & 0 & { - \theta_{7} } \\ \end{array} } \right]. $$
(87.7)

It can be seen that the pair \( (A,B) \) is controllable, and \( (A,C) \) is observable.

3 Adaptive Observer Design

In this section, an adaptive observer will be developed for the unmeasured states x and f(t). And then, another observer for w(t) will be presented to asymptotically recover w(t) and its any order time derivatives. The first observer scheme is mainly improved on [4].

To estimate the states x, from (87.6), we interpret the following observer

$$ \dot{\hat{x}} = A\hat{x} + Bu + D\hat{f}(t) + K_{1} (y - C\hat{x}) $$
(87.8)

where \( \hat{x} \) is the estimate of x, \( K_{1} = [k_{11} ,k_{12} ,k_{13} ]^{ \top } \) is such that the matrix \( (A - K_{1} C) \) is Hurwitz, \( \hat{f}(t) \) denotes the estimate of f(t) and is given by

$$ \hat{f} = C(x - \xi ),\quad \dot{\xi } = A\hat{x} + Bu + D\hat{f} + K_{2} (y - C\hat{x}) $$
(87.9)

where \( K_{2} = [k_{21} ,\,k_{22} ,\,k_{23} ]^{ \top } \) is a vector of control gains to be determined later.

Let \( \tilde{x} = x - \hat{x} \) and \( \tilde{f} = f - \hat{f} \) be the estimation errors. Then, from (87.6), (87.8) and (87.9), we yield the observation error dynamics as follows

$$ \begin{aligned} \dot{\tilde{x}} = & (A - K_{1} C)\tilde{x} + D\tilde{f} \hfill \\ \dot{\tilde{f}} = & - C(A + K_{2} C)\tilde{x} - CD\tilde{f} + \dot{f}. \hfill \\ \end{aligned} $$
(87.10)

Proposition 1

Consider the observation error dynamics (87.10). Under Assumption 2, if there exists a symmetric, positive-definite matrix M satisfying

$$ \left[ {\begin{array}{*{20}c} {A - K_{1} C} & D \\ { - C(A + K_{2} C)} & { - CD} \\ \end{array} } \right]^{ \top } M + M\left[ {\begin{array}{*{20}c} {A - K_{1} C} & D \\ { - C(A + K_{2} C)} & { - CD} \\ \end{array} } \right] \le \lambda I,\,M\left[ {\begin{array}{*{20}c} 0 \\ 0 \\ 1 \\ \end{array} } \right] = \begin{array}{*{20}c} 0 \\ 0 \\ 1 \\ \end{array} $$

with λ a positive constant and I an identity matrix, then the estimation errors\( \tilde{x} \) and \( \tilde{f} \) are globally convergent to a bounded area around the origin.

Proof

Consider the following Lyapunov function \( V_{0} = [\tilde{x}^{ \top } ,\,\tilde{f}]M[\tilde{x}^{ \top } ,\,\tilde{f}]^{ \top } . \) Differentiating it along the solutions of (87.10), we yield

$$ \dot{V}_{0} \le - \lambda (\tilde{x}^{ \top } ,\,\tilde{x} + \tilde{f}^{2} ) + 2\tilde{f}\dot{f}. $$

Due to the Young’s inequality and \( \left| {\dot{f}} \right| \le \sigma_{f} , \) we have

$$ \dot{V}_{0} \le - \lambda \tilde{x}^{ \top } \tilde{x} - \lambda_{f} \tilde{f}^{2} + \varepsilon_{1}^{ - 1} \sigma_{f}^{2} \le - \eta V_{0} + \varepsilon_{1}^{ - 1} \sigma_{f}^{2} $$

where \( \lambda_{f} = \lambda - \varepsilon_{1} \) and \( \eta = {{\lambda_{f} } \mathord{\left/ {\vphantom {{\lambda_{f} } {\bar{l}}}} \right. \kern-\nulldelimiterspace} {\bar{l}}},\,\varepsilon_{1} \) is a positive constant such that \( \lambda_{f} > 0 \) and \( \bar{l} \) is the maximum eigenvalue of the matrix M. Then, one can see that \( V_{0} (t) \) globally converges to a ball around zero with the radius \( \sigma_{f}^{2} /\varepsilon_{1} \eta . \) As a consequence, the estimation errors \( (\tilde{x},\,\tilde{f}) \) converge to a ball centered at the origin with the radius \( {{\sigma_{f} } \mathord{\left/ {\vphantom {{\sigma_{f} } {\sqrt {\varepsilon_{1} \eta \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{l} } }}} \right. \kern-\nulldelimiterspace} {\sqrt {\varepsilon_{1} \eta \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{l} } }}, \) with, where \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{l} \) is the minimum eigenvalue of M.

In the rest of this section, we will design an observer for w(t). At first, it worth noting that the dynamics of w(t) can be expressed as

$$ \dot{W} = S_{w} W,\,\ddot{w} = C_{w} W $$
(87.11)

with \( W \in {\mathbb{R}}^{2n} ,\,S_{w} = {\rm{block}}\,{\rm{diag}}[S_{1} , \ldots S_{n} ] \) and \( C_{w} = [C_{1} , \ldots ,C_{n} ], \) where \( S_{i} = \left[ {\begin{array}{*{20}c} 0 & {\omega_{i} } \\ { - \omega_{i} } & 0 \\ \end{array} } \right],\,C_{i} = \left[ {\omega_{i}^{2} ,\,0} \right],\,\forall i \in [1,n]. \) Note that \( S_{w} \) and \( C_{w} \) are known under Assumption 1, and the pair \( (S_{w} ,C_{w} ) \) is observable. Since \( \ddot{w} \) is assumed to be a known variable, then the following observer is designed

$$ \dot{\hat{W}} = S_{w} \hat{W} + K_{3} (\ddot{w} - C_{w} \hat{W}),\,\hat{\ddot{w}} = C_{w} \hat{W} $$
(87.12)

where \( \hat{W} \) and \( \hat{\ddot{w}} \) are the estimates, \( K_{3} \in {\mathbb{R}}^{2n} \) is such that the matrix \( (S_{w} - K_{3} C_{w} ) \) is Hurwitz. This observer can be used to reconstruct any order time derivative of w(t).

Proposition 2

The output of system (87.12) defined as

$$ \hat{w}^{(i)} = C_{w} S_{w}^{i - 2} \hat{W},\quad\forall i \ge 0 $$
(87.13)

yields converging estimate of the ith order derivative of w (t).

Proof

From (87.11), one can see that the i th order derivative of w(t) can be given as \( w^{(i)} = C_{w} S_{w}^{i - 2} W. \) Then, we have

$$ w^{(i)} - \hat{w}^{(i)} = C_{w} S_{w}^{i - 2} (W - \hat{W}) $$

Let \( \tilde{W} = W - \hat{W} \) be the estimation error and choose the Lyapunov function candidate \( V_{1} = \tilde{W}^{ \top } \tilde{W}. \) Differentiating \( V_{1} \) along the solutions of (87.11) and (87.12), we have

$$ \dot{V}_{1} = \tilde{W}^{ \top } (S_{w} - K_{3} C_{w} )\tilde{W} $$

which implies that \( \mathop {\lim }\nolimits_{t \to \infty } \left\| {\tilde{W}} \right\| = 0 \) due to the fact that \( (S_{w} - K_{3} C_{w} ) \) is Hurwitz. Then, one can obtain \( \mathop {\lim }\nolimits_{t \to \infty } \left| {w^{(i)} - w^{(i)} } \right| = \mathop {\lim }\nolimits_{t \to \infty } \left| {C_{w} S_{w}^{i - 2} (W - \hat{W})} \right| = 0. \)

4 Controller Design

At first, we want to note that the structure of the system (87.8) allows us to use the Lyapunov’s direct method and backstepping technique for the controller design procedure, which can be divided into three steps.

  1. Step 1.

    Consider the Lyapunov function candidate \( V_{2} = 0.5\gamma_{{1}}\,{{\bar{e}^{2} }} , \) where \( \gamma 1 \) is a positive constant to be chosen later. The time derivative of \( V_{2} \) is given by

$$ \dot{V}_{2} = \gamma_{{1}}^{{\bar{e}}} ( - \theta_{2} \hat{x}_{1} + \theta_{1} \hat{x}_{2} + \theta_{3} \hat{f} + K_{11} C\tilde{x} + \hat{\dot{w}}). $$
(87.14)

Let \( \hat{x}_{2e} = \hat{x}_{2} - \alpha_{2} \) be the error state with \( \alpha_{2} \) a virtual control of \( \hat{x}_{2} . \) Choosing \( \alpha_{2} \) as

$$ \alpha_{2} = \theta_{1}^{ - 1} ( - k_{e} \bar{e} + \theta_{2} \hat{x}_{1} - \theta_{3} \hat{f} - \hat{\dot{w}}) $$
(87.15)

with \( k_{e} \) a positive constant, and substituting (87.15) into (87.14), we have

$$ \dot{V}_{2} = - k_{e} \gamma_{1} \bar{e}^{2} + \gamma_{1} \bar{e}^{2} (\theta_{1} \hat{x}_{2e} + k_{11} C\tilde{x}). $$
(87.16)
  1. Step 2.

    To regulate the new error \( \hat{x}_{2e} , \) we choose the Lyapunov function candidate \( V_{3} = V_{2} + 0.5\gamma_{2} \hat{x}_{2e}^{2} \) with \( \gamma_{2} > 0. \) The dynamics of \( V_{3} \) satisfies

$$ \begin{aligned} \dot{V}_{3} = & - k_{e} \gamma_{1} \bar{e}^{2} + \gamma_{1} \bar{e}(\theta_{1} \hat{x}_{2e} + k_{11} C\tilde{x}) \\ & + \gamma_{2} \hat{x}_{2e} ( - \theta_{4} \hat{x}_{1} - \theta_{5} \hat{x}_{2} + \theta_{6} \hat{x}_{3} + k_{12} C\tilde{x} - \dot{\alpha }_{2} ). \end{aligned} $$
(87.17)

Let \( \hat{x}_{3e} = \hat{x}_{3} - \alpha_{3} \) be the virtual control error, and \( \alpha_{3} \) is given by

$$ \alpha_{3} = \theta_{6}^{ - 1} ( - k_{x} \hat{x}_{2e} + \theta_{4} \hat{x}_{1} + \theta_{5} \hat{x}_{2} + \zeta_{1} ) $$
(87.18)

with \( k_{x} \) a control gain to be determined later, and

$$ \zeta_{1} = - \theta_{1}^{ - 1} [k_{e} ( - \theta_{2} \hat{x}_{1} + \theta_{1} \hat{x}_{2} + \theta_{3} \hat{f} + \hat{\dot{w}}) - \theta_{2} \dot{\hat{x}}_{1} + \hat{\ddot{w}}]. $$
(87.19)

Substituting (87.18) and (87.19) into (87.17) and according to the expression of \( \dot{\alpha }_{2} , \) we yield

$$ \begin{aligned} \dot{V}_{3} = & - k_{e} \gamma_{1} \bar{e}^{2} + \gamma_{1} \bar{e}(\theta_{1} \hat{x}_{2e} + k_{11} C\tilde{x}) \\ & - k_{x} \gamma_{2} \hat{x}_{2e}^{2} + \gamma_{2} \hat{x}_{2e}^{2} (\theta_{6} \hat{x}_{3e} + \bar{k}_{12} C\tilde{x} + \theta_{1}^{ - 1} \theta_{3} \dot{\hat{f}}). \end{aligned} $$
(87.20)

with \( \bar{k}_{12} = k_{e} k_{11} \theta_{1}^{ - 1} + k_{12} . \)

  1. Step 3.

    This is the final step. To regulate the error state \( \hat{x}_{3e} , \) we consider the Lyapunov function \( V_{4} = V_{3} + 0.5\gamma_{3} \hat{x}_{3e}^{2} \) with \( \gamma_{3} > 0. \) The time derivative of \( V_{4} \) is

$$ \dot{V}_{4} = \dot{V}_{3} + \gamma_{3} \hat{x}_{3e} ( - \theta_{7} \hat{x}_{3} + \theta_{8} i + k_{13} C\tilde{x} - \dot{\alpha }_{3} ). $$
(87.21)

Then, we choose the input i as

$$ i = \theta_{8}^{ - 1} ( - k_{i} \hat{x}_{3e} + \theta_{7} \hat{x}_{3} - \bar{k}_{13} C\tilde{x} + \zeta_{2} ) $$
(87.22)

with

$$ \zeta_{2} = - k_{x} \hat{x}_{3e} + \theta_{6}^{ - 1} [\zeta_{1} \dot{\hat{x}}_{1} + \zeta_{2} \dot{\hat{x}}_{2} + k_{x}^{2} \hat{x}_{2e} - \theta_{1}^{ - 1} (k_{e} \hat{w}^{(3)} + \hat{w}^{(4)} )] $$
(87.23)

where \( k_{i} \) is a control gain, \( \bar{k}_{13} = k_{13} + \theta_{6}^{ - 1} k_{x} \bar{k}_{12} ,\,\zeta_{1} = \theta_{4} + \theta_{1}^{ - 1} \theta_{2} (k_{e} - \theta_{2} ) \) and \( \zeta_{2} = \theta_{5} - k_{e} + \theta_{2} . \) Substituting (87.22) and (87.23) into (87.21) and following (87.20) and the definition of \( \alpha_{3} , \) we have

$$ \begin{aligned} \dot{V}_{4} = & - k_{e} \gamma_{1} \bar{e}^{2} (\theta_{1} \hat{x}_{2e} + k_{11} C\tilde{x}) - k_{x} \gamma_{2} \hat{x}_{2e}^{2} + \gamma_{2} \hat{x}_{2e}^{2} (\theta_{6} \hat{x}_{3e} \\ & + \bar{k}_{12} C\tilde{x} + \theta_{1}^{ - 1} \theta_{3} \dot{\hat{f}}) - k_{i} \gamma_{3} \hat{x}_{3e}^{2} + \gamma_{3} \hat{x}_{3e}^{2} (\zeta_{3} \dot{\tilde{x}} + \zeta_{4} \dot{\hat{f}}) \end{aligned} $$
(87.24)

with \( \zeta_{3} = - \theta_{2} k_{11} {C \mathord{\left/ {\vphantom {C {\theta_{2} \theta_{6} }}} \right. \kern-\nulldelimiterspace} {\theta_{2} \theta_{6} }} \) and \( \zeta_{4} = - \theta_{3} {{(k_{x} + k_{e} + \theta_{2} )} \mathord{\left/ {\vphantom {{(k_{x} + k_{e} + \theta_{2} )} {\theta_{2} \theta_{6} }}} \right. \kern-\nulldelimiterspace} {\theta_{2} \theta_{6} }}. \) Then, we can state our main result of this chapter in the following theorem.

Theorem 1

Consider the system (87.6) with the output-feedback controller (87.22) and the observers given in (87.8) and (87.12). Under Assumption 1 and 2, the heave compensation error\( e(t) \)asymptotically tends to a small bounded area around the origin.

Proof

From (87.8) and (87.9), we can rewrite (87.24) as

$$ \begin{aligned} \dot{V}_{4} = & - k_{e} \gamma_{1} \bar{e}^{2} + \gamma_{1} \theta_{1} \bar{e}\hat{x}_{2e} ( + k_{11} C\tilde{x}) - k_{x} \gamma_{2} \hat{x}_{2e}^{2} + \gamma_{2} \theta_{6} \hat{x}_{2e} \hat{x}_{3e} - k_{i} \gamma_{3} \hat{x}_{3e}^{2}\\ & + (\Upomega_{1} \bar{e} + \Upomega_{1} \hat{x}_{2e} + \Upomega_{3} \hat{x}_{3e} )\tilde{x} + (\Upomega_{4} \bar{e} + \Upomega_{5} \hat{x}_{2e} + \Upomega_{6} \hat{x}_{3e} )\tilde{f} \end{aligned} $$

with \( \Upomega_{i}^{ \top } \, \in {\mathbb{R}}^{3} (i = 1,2,3) \) and \( \Upomega_{i} \, \in {\mathbb{R}}\ (i = 4,5,6) \) the appropriate vectors and scalars, respectively. By using the Young’s inequalities and from Proposition 1, after a lengthy but simple calculation, we have

$$ \dot{V}_{4} \le - \bar{k}_{e} \bar{e}^{2} - \bar{k}_{x} \hat{x}_{2e}^{2} - \bar{k}_{i} \hat{x}_{3e}^{2} + \Lambda $$

with \( \bar{k}_{e} = k_{e} \gamma_{1} \varepsilon_{2} {{(\gamma_{1} \theta_{1} + 2)} \mathord{\left/ {\vphantom {{(\gamma_{1} \theta_{1} + 2)} 2}} \right. \kern-\nulldelimiterspace} 2},\,\bar{k}_{x} = k_{x} \gamma_{2} - {{\gamma_{1} \theta_{1} } \mathord{\left/ {\vphantom {{\gamma_{1} \theta_{1} } {2\varepsilon_{2} - {{\varepsilon_{3} (\gamma_{2} \theta_{6} + 2)} \mathord{\left/ {\vphantom {{\varepsilon_{3} (\gamma_{2} \theta_{6} + 2)} 2}} \right. \kern-\nulldelimiterspace} 2}}}} \right. \kern-\nulldelimiterspace} {2\varepsilon_{2} - {{\varepsilon_{3} (\gamma_{2} \theta_{6} + 2)} \mathord{\left/ {\vphantom {{\varepsilon_{3} (\gamma_{2} \theta_{6} + 2)} 2}} \right. \kern-\nulldelimiterspace} 2}}},\,\bar{k}_{i} = k_{i} \gamma_{3} - {{\gamma_{2} \theta_{6} } \mathord{\left/ {\vphantom {{\gamma_{2} \theta_{6} } {2\varepsilon_{3} - \varepsilon_{4} }}} \right. \kern-\nulldelimiterspace} {2\varepsilon_{3} - \varepsilon_{4} }} \) and \( \Lambda = \sigma_{f}^{2} (\varepsilon_{1} \eta \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{l} )^{ - 1} [\sum\nolimits_{i = 1}^{3} {{{(\| {\Upomega_{i} }\| + | {\Upomega_{i + 3} }|^{2} )} \mathord{/ {\vphantom {{(\| {\Upomega_{i} }\| + | {\Upomega_{i + 3} }|^{2} )} {2\varepsilon_{i + 1} }}}\kern-\nulldelimiterspace} {2\varepsilon_{i + 1} }}} ], \) where \( \varepsilon_{i} (i = 2,3,4) \) are chosen such that the control gains \( \bar{k}_{e} ,\,\bar{k}_{x} \) and \( \bar{k}_{i} \) are positive. Then, following the proof of Proposition 1, one can conclude that the error states \( (\bar{e},\,\hat{x}_{2e} ,\,\hat{x}_{3e} ) \) globally asymptotically converge to a bounded ball centered at zero with the radius \( \sqrt {{ \Lambda \mathord{\left/ {\vphantom { \Lambda {\bar{\eta }}}} \right. \kern-\nulldelimiterspace} {\bar{\eta }}}} , \) where \( \bar{\eta } = {{2\min (\bar{k}_{e} ,\,\bar{k}_{x} ,\,\bar{k}_{i} )} \mathord{\left/ {\vphantom {{2\min (\bar{k}_{e} ,\,\bar{k}_{x} ,\,\bar{k}_{i} )} {\max (\gamma_{1} ,\,\gamma_{2} ,\,\gamma_{3} )}}} \right. \kern-\nulldelimiterspace} {\max (\gamma_{1} ,\,\gamma_{2} ,\,\gamma_{3} )}}. \) Furthermore, it is not hard to check that this radius can be made arbitrarily small by choosing the gains, \( k_{e} ,\,k_{x} \) and \( k_{i} , \) sufficiently large.

For e(t) from Proposition 1, 2 and above result, we have

$$ \mathop {\lim }\limits_{t \to \infty } \left| {e(t)} \right| \le \mathop {\lim }\limits_{t \to \infty } \left| {\bar{e}(t)} \right| + \mathop {\lim }\limits_{t \to \infty } \left| {x_{1} - \hat{x}_{1} } \right| + \mathop {\lim }\limits_{t \to \infty } \left| {\dot{w} - \hat{\dot{w}}} \right| \le \sqrt {{ \Lambda \mathord{\left/ {\vphantom { \Lambda {\bar{\eta }}}} \right. \kern-\nulldelimiterspace} {\bar{\eta }}}} + {{\sigma_{f} } \mathord{\left/ {\vphantom {{\sigma_{f} } {\sqrt {\varepsilon_{1} \eta \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{l} } }}} \right. \kern-\nulldelimiterspace} {\sqrt {\varepsilon_{1} \eta \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{l} } }}. $$

This means that the trajectory of e(t) reduces to a bounded value as time goes to infinity, which completes this proof.

5 Simulation Results

To illustrate the effectiveness of the proposed controller and observer, we carry out some simulations in this section. The system parameters are given by: \( \theta_{1} = 390,\,\theta_{2} = 0.04,\,\theta_{3} = 0.001,\,\theta_{4} = 490.75,\,\theta_{5} = \theta_{6} = 1.0,\,\theta_{7} = 157.233,\,\theta_{8} = 1.02{\text{e}}7 \) and \( f(t) = 1000 + \sin (15t). \) The desired velocity is \( c = 0. \) The harmonics \( w(t) \) is set as

$$ w(t) = \sin (4.3t - 0.4\pi ) + 1.5\sin (4.8t + 0.3\pi ) + 0.7\sin (5.3t). $$

The controller and observer gains are chosen as: \( k_{e} = 100,\,k_{x} = k_{i} = 150,\,K_{1} = [500,\, - 490.75,\,0]^{ \top } ,\,K_{2} = [0.04,\,0,\,]^{ \top } \) and \( K_{3} = [2,\,0,\,4,\,0,\,0,\,5]^{ \top } . \) The initial conditions of the system and observer are selected at the origin. The simulation results are depicted in Figs. 87.2 and 87.3.

Fig. 87.2
figure 2

The time evaluation of e(t)

Full size image
Fig. 87.3
figure 3

Short presentations of the estimation errors

Full size image

From Fig. 87.2, one can see that the tracking error \( e(t) \) converges a small area around the origin as expected. The plots in Fig. 87.3 show a short time presentation of the convergence of the observation errors. It can be seen that the estimation error \( \ddot{w} - \hat{\ddot{w}} \) is asymptotically stable and the error \( \dot{x}_{h} - \dot{\hat{x}}_{h} \) does not converge to zero due to the fact that the term \( f(t) \) is time-varying.

6 Conclusions

In this chapter, a control strategy for an active heave compensation system is presented. For the system with unknown disturbances and unmeasurable states, two observers are designed respectively to estimate the system states and asymptotically reconstruct the vessel motion represented by a set of harmonic signals. By using the Lyapunov’s direct method and backstepping technique, a output-feedback tracking controller is presented. The effectiveness of the proposed control strategy is tested by means of simulations.