Forward and Reverse Modeling of Low Noise Amplifiers Based on Circuit Simulations

Abstract

Forward and reverse modeling of RF circuit blocks are useful approaches in design space exploration. The underlying idea of forward modeling is the creation of accurate surrogate models, which can be used to predict the circuit performances replacing (expensive) circuit simulations. On the other hand, reverse modeling concerns multiobjective optimization to explore relevant trade-offs between performances. This paper provides a discussion of application of surrogate models and multiobjective optimization to narrow-band low noise amplifier design. We discuss numerical difficulties encountered when the forward model is derived by using surrogate models of low noise amplifier admittances to compute performance figures via analytical equations. Afterward, we provide an example where direct performace modeling leads to a more accurate result even when the simplest surrogate model type (a lookup table) is used. Finally, a detailed tutorial of the normal boundary intersection optimization method is provided.

1 Introduction

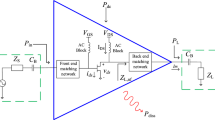
An RF circuit block, such as a Low Noise Amplifier (LNA), shown in Fig. 5.1, is characterized by performance figures (e.g., voltage gain, linearity, noise figure, etc.) which are functions of the design parameters (e.g., width and length of transistors, bias conditions, values of passive components) [10]. The goal of the design process is to figure out one or more sets of design parameters resulting in a circuit which fulfills the specifications, i.e., constraints given on the performances.

Fig. 5.1

Schematic of a (weakly-nonlinear) narrowband low noise amplifier. Most important design parameters, on which performances depend on, are: transistor width W, inductances L _s and L _m , frequency f, and bias condition V _GS and transistor length L

Nowadays most of the RF integrated circuit design methods are still based on experience. Typically, circuit designers start guessing one or more solutions of the design problem, possibly relying on simplified mathematical models reflecting coarse approximations of the physics describing the circuit. Afterwards, they verify the circuit behavior through circuit simulations, which instead exploit highly accurate models of electronic components. Design parameters are then adjusted until circuit specifications are achieved. Hence, there is a demand from industry for the development of systematic methods and tools, which fill the gap between the generality of several existing modeling and optimization software and the concrete applications at hand.

The design problem can be formulated as a single objective optimization problem, where a single performance or a weighted sum of performances is minimized. For example, typical LNA design strategies try to minimize noise figure (NF) (e.g. [12]) or power dissipation or to maximize linearity, while enforcing proper constraints on the remaining performances.

A more insightful and systematic approach than single objective optimization, even though computationally more expensive, is multi-objective optimization. Circuit performances normally are in conflict with each other: for instance, to improve the voltage gain of an LNA, the linearity has to be reduced. Hence, a multiobjective optimization method (e.g. the normal boundary intersection algorithm (NBI) [3, 16] or the strength pareto evolutionary algorithm 2 (SPEA2) [15, 20]) can be used to figure out and graphically display such trade-offs as Pareto fronts. Since the sample points belonging to a Pareto front are obtained by optimizing performances with respect to design parameters, the result of such multiobjective optimization is a ‘reverse model’ of the circuit block, which determines a correspondence between samples of the Pareto front and samples belonging to the design space.

Design tools based on optimization methods can be classified in two categories: simulation-based tools and stand-alone tools. To compute circuit performances in the optimization loop, the former category of tools calls a commercially available circuit simulator, such as Spectre or Hspice. The second category includes a built-in performance evaluation module based on a symbolic performance model of the circuit [11, 14, 18]. Although symbolic models enable a faster evaluation of performances than circuit simulations, their accuracy is lower. For this reason, the authors of [18] propose to use their tool as an “auxiliary tool generating an initial design for a commercial design environment”. On the other hand, an extensive exploration of the design space with simulation-based tools is limited by the high computational cost of numerical simulations.

In this work, a simulation-based methodology, aiming to combine accuracy of circuit simulations with computational efficiency of symbolic models, is described. Circuit simulations are replaced by a cheap-to-evaluate surrogate model, derived from a proper set of precomputed simulations [ 6, 7, 14, 19]. An approximation of the circuit performance figures based on one or more surrogate models is referred to as ‘forward model’ of the circuit. A forward model can be either obtained via direct modeling of circuit performances or by using surrogate models of a convenient set of behavioural parameters (e.g. admittances and noise functions) to compute performances via analytical equations. The former approach involves the direct approximation of the function:

$$ {\mathbf{p}} = {\mathbf{p}}({\mathbf{x}},{\mathbf{y}}), $$

(5.1)

where $\mathbf{p}=(p_1 \cdots p_j)$ is the vector of circuit performances, $\mathbf{x}=(x_1 \cdots x_k)$ is the vector of design parameters and $\mathbf{y}=(y_1 \cdots y_l)$ is a vector holding extra-circuit parameters (e.g. load impedances). Surrogate modeling involves the identification of a vector of functions:

$$ \tilde{{\mathbf{p}}} = \tilde{{\mathbf{p}}}({\mathbf{x}},{\mathbf{y}}), $$

(5.2)

such that $\tilde{\mathbf{p}} \approx \mathbf{p}.$

Circuit performances can also be written as functions of the behavioural parameters $\mathbf{b}=\mathbf{b}(\mathbf{x})$ and the extra-parameters $\mathbf{y}:$

$$ {\mathbf{p}} = {\mathbf{p}}({\mathbf{b}}({\mathbf{x}}),{\mathbf{y}}). $$

(5.3)

The latter modeling approach consists in the approximation of the behavioural parameters $\mathbf{b}=\mathbf{b}(\mathbf{x})$ through the surrogate models $\tilde{\mathbf{b}}=\tilde{\mathbf{b}}(\mathbf{x})$, such that $\tilde{\mathbf{b}} \approx \mathbf{b}$. The forward model is then given by:

$$ \tilde{{\mathbf{p}}} = {\mathbf{p}}(\tilde{{\mathbf{b}}}({\mathbf{x}}),{\mathbf{y}}). $$

(5.4)

Modeling of behavioural parameters is attractive because they do not depend on the extra-parameters y, therefore the approximation problem is simplified. However, in this paper we show that forward modeling from behavioural parameters is likely to introduce an unacceptable amplification of the numerical error, i.e. $\tilde{\mathbf{b}} \approx \mathbf{b}$ does not necessarily imply that $\tilde{\mathbf{p}} \approx \mathbf{p}$. Therefore, direct approximation of performances has to be currently preferred, even though the inclusion of all circuit parameters in the model is still an open problem.

Methods described in this paper have been implemented into a prototype of an auxiliary design tool. Currently, it can only handle narrowband LNA design and does disregard circuit layout optimization. Further extensions can enable wideband and multiband LNAs design [5, 12], and layout-level optimization [13].

The paper is organized as follows. In Sect. 5.2, forward and reverse modeling problem descriptions are introduced. Section 5.3 focuses on forward modeling and the numerical error amplification problem. Section 5.4 describes reverse modeling via NBI optimization technique. Section 5.5 explains how a reverse model can exploit a forward model to speed-up the computation of a Pareto-front. Section 5.6 discusses presented results and concludes the paper.

2 Forward and Reverse Modeling: Problem Descriptions

A forward model of a circuit determines a correspondence between design parameters and its performances. It involves the generation of a set of surrogate models or response surface models (RSMs), which are cheaper to evaluate than the set of circuit simulations needed for evaluating the same performances. On the other hand, a reverse model links Pareto-optimal points of the performance space with the corresponding design parameters.

A block diagram showing the connection between circuit simulations, surrogate models, design parameters and performances is depicted in Fig. 5.2. Computational times are indicative. In particular, the computational time needed to generate the forward model depends on the specific set of functions that are approximated via surrogate modeling.

Fig. 5.2

Block diagram showing the connection between circuit simulations, surrogate models, design parameters and performances

A typical setup used to build a forward model of an RF circuit block consists of modeling software (e.g. the SUMO Toolbox [17]) linked to a circuit simulator. The modeling software directly drives the circuit simulator, requesting new simulations in order to accurately cover the entire design space. Additional data samples may be selected according to adaptive sampling techniques, to allocate more samples in those regions of the design space which are more difficult to model and/or where the error is the largest [1]. This way, the obtained model is intended to be valid throughout the entire design space. This approach was adopted in [6, 7].

Several design problems can be formulated as multiobjective optimization problems, involving the simultaneous optimization of two or more conflicting objectives subject to constraints. For instance, for an LNA one wants to maximize linearity IIP2 but at the same time, maximize the voltage gain A _v as well. Since these are two conflicting objectives, the trade-off has to be studied. One way to do this is to compute a Pareto-front. An example is given in Fig. 5.3.

Fig. 5.3

Pareto-front representing the trade-off between voltage gain A _v and linearity IIP2 of an LNA. Left: design space. Right: performance space

The final result of such optimization process is a reverse model, which provides the design parameters corresponding to each Pareto-optimal solution. In the example shown in Fig. 5.3, the left side plot shows the points of the design space (W _n , L _mn ) ¹ which correspond to the Pareto-optimal points of the right side plot.

Since the construction of a reverse model requires a lot of performance evaluations, it could exploit a forward model in order to make the computation of Pareto-front fast. This will be shown in Sect. 5.4.

3 Forward Modeling

Forward modeling of RF circuit blocks is a challenging research area, since it demands to obtain accurate models with a small number of data samples distributed in high dimensional design spaces. For instance, a forward model of an LNA should provide the following performance figures: power consumption P, voltage gain A _v , input reflection $\Upgamma_a$, second-order linearity IIP2, third-order linearity IIP3 and noise figure NF, as functions of the most important design parameters.

In [7] the authors used the SUMO Toolbox [17] to generate surrogate models of LNA behavioral parameters (admittances and noise functions). Such behavioral parameters were given by a simplified analytic model, in order to allow a fast model identification. It was tried to achieve a Root Relative Square Error (RRSE) $\leq 0.05$ with a maximum number of samples of 1500. Results indicated that this is possible only including the first four parameters as ‘inputs’ of the model W, L _s , f, L (when V _GS and L _m are kept constant).

A study reported in [4] considers a complete characterization of an LNA provided by circuit simulations. This includes the complete set of admittances needed to describe the weakly non-linear behavior [2], which were not taken into account in [7], but the number of inputs was limited to two (W and L _s ). Results indicate that a greater number of samples is needed to achieve a similar level of accuracy as using the analytic model.

In order to build a forward model, surrogate models of admittances and noise functions have to be used to compute performances (P, A _v , $\Upgamma_a$, IIP2, IIP3 and NF), which are expressed as analytical functions of admittances and noise functions. ² This means that errors in the surrogate models may be amplified and hence result in inaccurate performance models (a general discussion of this issue is provided in the introduction). On the other hand, direct modeling of performances would require the inclusion of the source and load impedances, respectively Z _s and Z _l , as additional inputs (Fig.  5.1). ³ This would make the modeling more difficult. With the computation of performances from admittances and noise functions, the load conditions enter into the analytical expression and do not need to be modeled.

3.1 Performance Figures via Surrogate Models

Forward modeling from behavioural parameters is prone to introduce an unacceptable amplification of the surrogate model numerical error when computing circuit performances from behavioural parameter models. This is demonstrated by the following example.

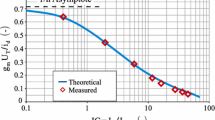
Performance figures are expected to be smooth functions, ‘local’ spikes are not expected. We computed IIP2 with respect to the design parameters W and L _s , by exploiting the models computed in [9] (Fig. 5.4). It is seen that several spikes appear. IIP2 can be expressed as function of the ratio of two voltages $v_{21}/v_{2p}$:

$$ IIP2 = 10\log_{10}\left[\left|\left({\frac{1000}{8R_S}}\right) \left({\frac{v_{21}}{v_{2p}}}\right)^2\right|\right], $$

(5.5)

where v ₂₁ is the voltage amplitude of the ‘wanted’ signal at output and v _2p is the voltage amplitude of ‘unwanted’ second harmonic at output [10]. It can be verified that all spikes are due to v _2p and ${{1}/{v_{2p}}}$, being v ₂₁ a smooth function.

Fig. 5.4

IIP2 as function of W and L _s (computed by means of surrogate models)

Furthermore, by decomposing v _2p into numerator and denominator $v_{2p}={\frac{num} {den}}$ it can be verified that, being den a smooth function, all the peaks are due to num and 1/num (Fig. 5.5).

Fig. 5.5

Magnitude of v _2p denominator, numerator and inverse of numerator

In particular, ‘positive’ peaks of IIP2 are due to peaks of ${\frac{1} {num}}$. They appear when num assumes values close to zero. On the other hand, negative peaks of IIP2 are due to peaks of num .⁴

The origin of ‘negative’ peaks is easy to investigate, since the function num may be readily decomposed into a sum of several terms, which are functions of surrogate models. A complete analysis is out of scope of this paper, we just provide a single example. A subpart of num, num′, is proportional to the product of two admittance surrogate models: $num' \propto y_{10100p}y_{p000p0}$. The model of y _10100p has a small peak due to modeling errors, which is amplified when multiplied by y _p000p0, since it is located in the region of the main resonance of y _p000p0 (Fig. 5.6). This peak is reflected also onto IIP2.

Fig. 5.6

Magnitude of y _p000p0, y _10100p and $y_{p000p0}y_{10100p}$

4 Reverse Modeling with the NBI Method

As indicated in the introduction, a natural way to deal with trade-offs between performances is to use a suitable multiobjective optimization technique.

Multiobjective optimization algorithms can be categorized globally into deterministic and evolutionary methods. Examples of such methods are NBI method and SPEA2, respectively. In this paper, we focus on the NBI method [3].

To outline this method we have to introduce a few notions in a more formal mathematical setting. The design parameters and performance parameters are assumed to be in the design space $\fancyscript{D}$ and performance space $\fancyscript{P}$, respectively. We assume that the region $\fancyscript{D}$ is feasible, i.e., all design parameters in $\fancyscript{D}$ satisfy the imposed constraints:

$$ {\fancyscript{D}} = \{ {\mathbf{x}} \in {\fancyscript{R}}^m | \;{\mathbf{c}} ({\mathbf{x}}) \leq 0 \}\quad \hbox{ with } {\mathbf{c}} ({\mathbf{x}}) \in {\fancyscript{R}}^q. $$

(5.6)

The performance space $\fancyscript{P}$ contains all performance values resulting from feasible design values in the region $\fancyscript{D}$ after applying a performance function f. Furthermore, the performance values can also be constrained, i.e.,

$$ {\fancyscript{P}} = \{ {\mathbf{f}} \in {\fancyscript{R}}^n |\;\exists_{{\mathbf{x}} \in {\fancyscript{D}}} {\mathbf{f}} = {\mathbf{f}}({\mathbf{x}}), {\mathbf{g}} ({\mathbf{f}}) \leq 0 \}. $$

(5.7)

The general problem at hand is the minimization of several objectives simultaneously,⁵ i.e.,

$$ \mathop{\hbox{minimize}}\limits_{{{\mathbf{x}}} \in {{\fancyscript{D}}}} {\mathbf{f}}({\mathbf{x}}) = \left(\begin{array}{l} f_1({\mathbf{x}})\\ \vdots\\ f_n({\mathbf{x}})\\ \end{array}\right)\quad \hbox{ such that }{{\mathbf{g}}} ({\mathbf{f}}) \leq 0. $$

(5.8)

However, in general there is no single ${\mathbf{x}} \in \fancyscript{D}$ that minimizes all components $f_i, i=1,\ldots,n$ simultaneously. Consequently, the multi-objective optimization (5.8) leads to trade-off situations where it is only possible to improve one performance at the cost of another. A trade-off situation needs to be based mathematically on a so-called dominance relation between vectors (see for example [16]).

Definition 1

Let a and b be vectors in $\fancyscript{R}^n$. Vector ${\bf a}=(a_1,\ldots,a_n)$ is said to dominate vector ${\bf b}=(b_1,\ldots,b_n)$ if and only if

$$ {\mathbf{a}} \prec {\mathbf{b}}: \Leftrightarrow \forall_{i \in \{1,\ldots,n\}} (a_i \leq b_i)\wedge \exists_{i \in \{1,\ldots,n\}} (a_i < b_i). $$

(5.9)

With this definition, a performance vector $f^{ * }$ f* is said to be Pareto-optimal if it is nondominated within $\fancyscript{P}$, i.e.,

$$ \neg \exists_{{\mathbf{f}} \in {\fancyscript{P}}} [{\mathbf{f}} \prec {\mathbf{f}}^*]. $$

(5.10)

The set of all Pareto-optimal points is called the Pareto front of $\fancyscript{P}$. The set of points in the design space corresponding to the Pareto front are called the source of the Pareto front.

In literature there are several methods available to calculate the Pareto front. In this paper we will describe the commonly used Normal-Boundary Intersection method (NBI method [3, 16]). We will closely follow [16].

For simplicity reasons we describe the NBI method for the 2D case only. Thus, we assume the design space $\fancyscript{D}$ and performance space $\fancyscript{P}$ as given above (with m = n = 2). However, it can easily be extended to higher dimensions.

Description of the NBI algorithm

• 1. Start with individually minimizing f ₁ and f ₂ as a function of x, i.e., compute ${\bf f}^{*k}={\bf f}({\bf x}^{*k})=\text {min} \{f_k({\bf x}) | \; {\bf x} \in \fancyscript{D} \}, k=1,2.$

• 2. Determine the straight line $\fancyscript{L}$ in $\fancyscript{P}$ between these points f ^*1 and f ^*2.

• 3. Determine the vector n normal to this straight line, pointing into the direction of decreasing f.

• 4. Select N points f _k on the line $\fancyscript{L}$ between f ^*1 and ${\bf f}^{*2}:{\bf f}_k = \lambda_k {\bf f}^{*1} + (1-\lambda_k) {\bf f}^{*2}$ for some $0 \leq \lambda_k \leq 1.$

• 5. For each point f _k , find the point p _k that maximizes the distance along n in the direction of decreasing f, and starting in f _k .

• 6. The points ${\bf p}_k, 1 \leq k \leq N$ are on the Pareto front.

Notice that in fact the NBI method consists of N subproblems in which a 1D line search optimization problem has to be solved. Clearly, several modifications to the above approach can be made to speed up the calculations. However, we will not go into details here.

5 Reverse Modeling Using Transistor Level Simulations

The NBI algorithm described in Sect. 5.4 was tested by using a simplified analytical model of an LNA [7]. However, to obtain an accurate representation of trade-offs between competing performances, a transistor level simulator has to be used. In principle, NBI can directly drive a circuit simulator by requiring data samples needed in the optimization process. However, this is nearly infeasible in practice, because of the large amount of simulations needed (a typical order of magnitude is 10⁴, with a cost of about 2–3 minutes per simulation). A more applicable idea is the usage of a forward model as described in Sect. 5.3. However, the final accuracy of the Pareto-front may be poor even when surrogate models of behavioral parameters are fairly accurate, due to the error amplification process described in Sect. 5.3.1.

A better solution relies on the direct approximation of circuit performances, as explained in the introduction. With this approach, no error propagation from the behavioral parameter space to the performance space occurs. A simple precomputed lookup table, which is linearly interpolated when NBI requests a new performance evaluation, will be used to demonstrate the validity of this approach.

Despite of its simplicity, linear interpolation is a robust way to approximate a function, which is doable even in high dimensional spaces. Moreover, a lookup table is generated at the only cost of circuit simulations. There is not additional cost due to optimization of surrogate model parameters (e.g. training of a neural network and number of layers and neurons per layer optimization [4, 6, 7, 8]). Linear interpolation occurs when a new sample of the performance has to be used in the Pareto front computation and not in an earlier stage.

5.1 Numerical Results

In this section we show an example comparing forward model and lookup table methods to generate a Pareto-front (Fig. 5.7) with the NBI method. Similarly to Fig. 5.3, we show the trade-off between voltage gain A _v and linearity IIP2 with respect to the (normalized) design parameters W _n and L _mn (other design parameters are kept constant to convenient values). However, we remark that results in Fig. 5.3 were generated by relying on a simplified LNA analytical model [7], whereas here both forward model and lookup table are based on transistor-level circuit simulations. Details about surrogate models exploited in performance computations are given in [4]. The lookup table is a regular grid of 100 × 100 points. ⁶ However, it is evident that the number of circuit simulations for each design parameter taken into account, has to be reduced as the dimensionality of the considered design space is increased.

Fig. 5.7

Comparison between Pareto-fronts obtained with a lookup table and with a forward model (trade-off between voltage gain A _v and linearity IIP2 of an LNA). Left: design space. Right: performance space

It is readily seen from Fig. 5.3 that the forward model based on surrogate models of admittance function, returns a ‘sparse’ set of points which fail to approximate the Pareto-front. Indeed such inaccurate results could have been expected from the discussion developed in Sect. 5.3.1. On the other hand, the forward model based on the performance lookup table provides a reasonable front.

Finally, we note that in principle the error amplification effect discussed in Sect. 5.3.1, could be negligible if surrogate models had an error sufficiently lower than ones in [4]. However, in practice this is not easy to achieve. Moreover, how much accurate the models should be, and in which part of design space, are still open issues.

6 Discussion and Conclusions

This paper has reviewed forward and reverse modeling concepts of RF circuit blocks, referring to a narrowband LNA.

A number of conclusions can be drawn:

• In principle forward models can be exploited to speed-up the computation of Pareto-fronts (i.e. reverse modeling), but the accuracy can be limited by error amplification from the surrogate models of behavioral parameters (admittances and noise functions) to circuit performances.

  Direct modeling of circuit performances solves the problem of error amplification from behavioural parameters to performances (Sect. 5.3.1).

• NBI optimization is proven as a promising approach to investigate LNA performance trade-offs.

• Forward models based on performance lookup tables (and linear interpolation) are likely to be sufficient for obtaining accurate Pareto-fronts when only two design parameters are taken into account in the forward model.

However, an LNA design problem may have ten or more design variables. Therefore, possible limitations of the uniformly filled lookup tables are:

• Uniform sampling of performances would require a too large number of samples because of the oversampling of the smooth regions, where sensitivity of performances as functions of design parameters is modest. It is expected that adaptive sampling techniques are needed when more design parameters are considered [1, 4, 17].

• Interpolation of the resulting large lookup tables can be computationally less efficient than modeling such a large number of design variables (which on the other hand is technically much more challenging).

Some important points have to be investigated further:

• How does the lookup table approach scale to more design parameters?

• How can the lookup table be filled and processed in an efficient and accurate way?

• How accurate should a forward model be in order to be successfully used in reverse modeling?

Finally, the surrogate modeling approach implemented in [17] will be directly applied to performances, comparing the accuracy with the table-based method.