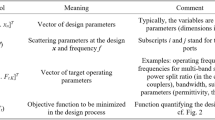
Abstract
The knowledge-intensive radiofrequency circuit design and the scarce design automation support play against the increasingly stringent time-to-market demands. Optimization algorithms are starting to play a crucial role; however, their effectiveness is dramatically limited by the accuracy of the evaluation functions of objectives and constraints. Accurate performance evaluation of radiofrequency passive elements, e.g., inductors, is provided by electromagnetic simulators, but their computational cost makes their use within iterative optimization loops unaffordable. Surrogate modeling strategies, e.g., Kriging, support vector machines, artificial neural networks, etc., arise as a promising modeling alternative. However, their limited accuracy in this kind of applications has prevented a widespread use. In this paper, inductor performance properties are exploited to develop a two-step surrogate modeling strategy in order to evaluate the behavior of inductors with high efficiency and accuracy. An automated design flow for radiofrequency circuits using this surrogate modeling of passive components is presented. The methodology couples a circuit simulator with evolutionary computation algorithms such as particle swarm optimization, genetic algorithm or non-dominated sorting genetic algorithm (NSGA-II). This methodology ensures optimal performances within short computation times by avoiding electromagnetic simulations of inductors during the entire optimization process and using a surrogate model that has less than 1% error in inductance and quality factor when compared against electromagnetic simulations. Numerous real-life experiments of single-objective and multi-objective low-noise amplifier design demonstrate the accuracy and efficiency of the proposed strategies.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The design of radiofrequency (RF) circuit blocks is becoming increasingly difficult in nanometer technologies. The design of blocks such as low-noise amplifiers (LNAs), voltage-controlled oscillators (VCOs) and power amplifiers (PAs) still highly depends on the experience of the RF designer.
Traditional circuit design methodologies usually follow a knowledge-based iterative procedure, as in Shaeffer and Lee (1997). Starting with specifications for a given circuit, a systematic step-by-step design procedure is applied to size each active and passive device in the circuit until the desired performances are obtained. This procedure uses a set of equations that must be specifically derived for each circuit topology, limiting, therefore, its general applicability. This kind of design approach presents another very important drawback: The analytical expressions that are used to model the circuit performances and the impact of the device physics are usually too simple and do not incorporate the impact of parasitic elements in active and passive devices (e.g., inductor parasitics). Therefore, this design procedure usually provides just an initial design point that still has to be refined by a number of design iterations involving also time-consuming electromagnetic (EM) simulations for passive structures like inductors and transformers. Another problem of this approach is that exploring the performance trade-offs of the circuit (e.g., power vs. noise figure in an LNA) can be very difficult.
In recent years, soft computing and, especially, evolutionary computation techniques are attracting much attention for the design of analog and RF circuits (Alpaydin et al. 2003; Fakhfakh et al. 2005; Liu et al. 2014a; Nieuwoudt et al. 2007a, b; Patanè et al. 2016; Póvoa et al. 2016; Ranter et al. 2002; Tulunay and Balkir 2008; Vancorenland et al. 2000; Xu et al. 2009). The use of optimization-based design methodologies tries to overcome the limitations of traditional methodologies by using an algorithm that performs a wide exploration of the design space to find one optimal design (single-objective optimization) or several optimal designs by creating a Pareto optimal front (multi-objective optimization).
Several strategies for optimization-based RF circuit design have been proposed in the literature (Fakhfakh et al. 2005; Liu et al. 2014a; Nieuwoudt et al. 2007a, b; Patanè et al. 2016; Póvoa et al. 2016; Ranter et al. 2002; Tulunay and Balkir 2008; Vancorenland et al. 2000; Xu et al. 2009). Reported approaches rely on accurate RF circuit simulators, or faster but inaccurate analytical equations to evaluate circuit performances within the optimization loop. A key ingredient in them is how passive components, especially inductors and transformers, are modeled. Some approaches rely on libraries provided by the foundries (Póvoa et al. 2016; Tulunay and Balkir 2008). However, these libraries provide limited inductor choices and, therefore, reduce the possibility of choosing an optimal inductor for a given application. Other approaches integrate accurate EM simulation of the inductors within the circuit optimization loop (Ranter et al. 2002). However, by using EM simulations, the optimization loop becomes very time-consuming and therefore the efficiency of the process dramatically deteriorates. A lumped element model (like the \(\uppi \)-model in Fig. 1) relating inductors performance parameters (namely inductance and quality factor) to the inductor geometric parameters is used in other approaches (Nieuwoudt et al. 2007a, b; Vancorenland et al. 2000; Xu et al. 2009). However, these models are not accurate, especially at high frequencies (Passos et al. 2015).
Surrogate inductor models arise as an attractive alternative aimed at combining the efficiency of analytical models with the accuracy of EM simulation (Passos et al. 2015). Surrogate models can be global or local. The former ones try to construct a high-fidelity model that is as accurate as possible over the complete search space. Once the model is built, it can be used as a fast performance evaluator in an optimization algorithm for inductor optimization (Mandal et al. 2008). However, it has been reported that these models may be highly inaccurate in some regions of the design space, yielding suboptimal results (Liu et al. 2011).
On the contrary, local models are iteratively improved during the inductor optimization process (Ballicchia and Orcioni 2010). An initial coarse model is first created by using a few electromagnetically simulated training points. Then, this coarse model is used within a population-based optimization algorithm and, at each iteration, promising solutions (typically one) are simulated electromagnetically. The data from these EM simulations are used to improve the accuracy of the surrogate model in the region where the new simulation points are added, while evolving toward the presumed optimal inductor. However, the results may highly depend on the accuracy of the initial coarse surrogate model. A prescreening technique, e.g., the expected improvement (EI) method, which can be used to increase the quality of the optimization process, consists in using the uncertainty measurement of the prediction, i.e., the mean square error (MSE), instead of just the predicted value to rank promising solutions. These methods have been widely applied to single-objective optimization (Jones et al. 1998; Paenke et al. 2006), and some more recent attempts have tried to extend these approaches to the multi-objective case, e.g., by using the hypervolume metric to evaluate the EI (Emmerich et al. 2006; Knowles 2006; Zhang et al. 2010). Some of these approaches, especially the single-objective ones, have been successfully exploited for optimization of RF passive devices (Liu et al. 2011).
For the sake of illustration, Fig. 2 shows the topology of a single-ended low-noise amplifier, containing four inductors, which will later be used for the experimental results in this paper. The above-described local approaches can hardly be applied to the optimization of RF circuits like this LNA since the optimization is performed at the circuit level, not the inductor level. Therefore, there is no guarantee that the inductors included in the circuit will converge to a certain region; furthermore, even if they converge to some region, the LNA typically contains several inductors and each may have very different characteristics. The scenario is even worse if we consider that we are also interested in multi-objective optimization at the circuit level in order to explore LNA design trade-offs, requiring, therefore, different inductors for each LNA.
The only approach to single-objective optimization of a RF circuit based on local models (a linear amplifier containing just one passive device: a transformer) has been reported in Liu et al. (2014b). The costly EM simulation of the transformer is replaced by a machine learning approach that progressively increases the accuracy of the local surrogate model of the transformer by adding the EM simulation results of promising transformers. The circuit optimization process decouples the design variables of the transformer from the rest of the circuit. To minimize the number of EM simulations, the less expensive circuit optimization loop is embedded within the more expensive transformer optimization loop. In this way, the synthesis of an RF amplifier is accomplished in some tens of hours of CPU time, which is still manageable. However, the approach is only valid for one single passive device (transformer), enabling in this way the outer transformer synthesis loop. However, this is not the case with most RF blocks, like those considered in this paper, which typically contain several inductors and/or transformers. On the other hand, since the outer design space exploration is based on a coarse surrogate model that is progressively refined with additional samples, there is a risk that the optimization process converges to a suboptimal region. This risk is certainly palliated by using prescreening approaches (not trivial in that embedded loop approach), but at the cost of additional EM simulations and therefore increased computation time.
It can be concluded that local models of passive devices are not a feasible strategy for single-objective and multi-objective optimizations of RF blocks involving several RF inductors and/or transformers. Therefore, the approach in this work focuses on increasing the accuracy of the global surrogate models of the inductors, enabling in this way optimized results with accuracy similar to EM simulation-based approaches and with efficiency close to approaches based on equivalent circuit models.
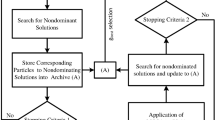
The general optimization methodology is shown in Fig. 3. The algorithm selects the circuit sizing (active and passive components) and also the inductor geometric parameters at each iteration. The surrogate model then evaluates the inductor behavior and transfers the S-parameter matrix files to the RF circuit simulator SpectreRF (Cadence SpectreRF circuit simulator).
The remainder of this paper is organized as follows: Sect. 2 describes the optimization-based design methodology for an essential class of RF circuits: LNAs. The proposed two-step surrogate modeling technique for the inductors is described in Sect. 3. Section 4 shows the experimental results for the optimization of LNAs, first with single-objective algorithms and, afterward, with a multi-objective optimization algorithm to get Pareto optimal fronts (POFs) of different sets of performances. Finally, in Sect. 5 conclusions are drawn.
2 LNA optimization strategy
2.1 Problem formulation
RF low-noise amplifiers are commonly found in radio communication circuits and are intended to amplify the low-power signals coming from the antenna without significantly degrading the signal-to-noise ratio.
The LNA performances that are usually considered during the design process are:
-
NF: noise figure, which accounts for the unwanted additional noise that the LNA injects in the input signal.
-
\(S_{21}\): gain.
-
\(P_\mathrm{DC}\): power consumption.
-
IIP3: third-order input intercept point, which accounts for the nonlinear performance of the LNA.
-
\(S_{11}\): input matching coefficient.
-
\(S_{22}\): output matching coefficient.
-
K: Rollett stability factor: If smaller than 1, the LNA is potentially unstable.
-
Area occupation, extremely important as it is directly related to the manufacturing cost in integrated circuit technologies.
During the design process, usually some of these performances are subject to some constraints while one or several ones (e.g., power consumption or area) are minimized or maximized, therefore becoming a constrained optimization problem:
where f(x) is a vector with m objective functions, g(x) is a vector with k constraints, and x is a vector with n design variables on the search space \(\Omega \).
When only one performance is minimized or maximized (\(m=1\)) the problem can be solved with a single-objective optimization algorithm. When two or more objectives are minimized/maximized (\(m>1\)), then either a weighted addition of the optimization objectives is minimized and a single-objective optimization algorithm is applied, or a multi-objective optimization algorithm is applied in case that a set of solutions showing the trade-offs between the different optimization objectives are sought for. In the multi-objective case, a solution a is said to constrain-dominate solution b if and only if a has a smaller constraint violation than b, or, if all constraints are met, \(f_{i}(a) \le f_{i}(b)\), for every \(i\in \{1,\ldots ,m\}\) and \(f_{j}(a)< f_{j}(b)\) for at least an index \(j\in \{1,{\ldots },m\}\). A point \(y\in \Omega \) is Pareto optimal if it is not dominated by any other point in \(\Omega \). The set of all the Pareto optimal solutions is the Pareto set (PS). The set of all the Pareto optimal objective vectors is the Pareto optimal front (POF).
It has also to be considered that some of the performances above, e.g., gain, noise figure, input and output matching, are frequency dependent and, therefore, design constraints and objectives must be usually considered over a frequency range.
2.2 Optimization algorithms
These optimization problems can be solved by an iterative loop involving an optimization algorithm that generates new candidate solutions at each iteration and a fitness function evaluator that provides the necessary information to compare and rank solutions. For single-objective optimization, the particle swarm optimization (PSO) algorithm and the genetic algorithm (GA) are used in our implementation. Genetic algorithms are evolutionary algorithms in which a population of solutions (individuals) evolve along a number of generations. At each iteration (generation) parent solutions are selected, crossed over and mutated to obtain an offspring population. Part of the parent–offspring populations survives to the following generation. In our implementation, a fitness-based selection scheme is applied (Mitchell 1996). PSO is a single-objective population-based stochastic optimization technique. As in evolutionary algorithms, the system is initialized with a population of random solutions and searches for optimal solutions by updating generations. However, unlike evolutionary algorithms, PSO has no evolution operators such as crossover and mutation. In PSO, the potential solutions, called particles, traverse the problem space with given velocities (Kennedy and Eberhart 1995). At each iteration, the velocity of each particle is updated according to its own inertia, its historical best position and the neighborhood best position. The standard PSO algorithm is designed to deal with unconstrained optimization problems. The LNA optimization problem posed in this paper is strongly constrained. Therefore, a tournament selection method has been implemented in PSO to handle design constraints (Deb 2010).
The non-dominated sorting genetic algorithm (NSGA-II) (Deb et al. 2002), which has been widely applied to diverse engineering problems (Khalesian and Delavar 2016; Shayeghi and Hashemi 2015), is used for multi-objective optimization in this paper. A major difference with single-objective optimization algorithms is the replacement of the fitness assignment concept by Pareto dominance. The POF is approximated by a finite number of points. It is desirable that the generated Pareto optimal points spread evenly in the POF, instead of clustering in a small part of the Pareto front. Diversity of solutions is pursued in NSGA-II by maximization of the minimal crowding distance. The same crossover and mutation operators than in the GA algorithm were used in this implementation.
2.3 Performance evaluation
The evaluation of objectives and constraints should be accurate enough and, at the same time, efficient enough to enable a reasonable computation time of the optimization process. The use of explicit analytical equations to evaluate the objectives and constraints of the LNA is discarded due to their low accuracy. An accurate evaluation is provided by RF electrical simulators.
The RF electrical simulator SpectreRF is used in our implementation to evaluate the LNA performances. The power consumption \(P_\mathrm{DC}\) is extracted from a DC analysis. An S-parameter analysis provides the gain, input matching and output matching, whereas a noise analysis provides the NF of the LNA. The Rollett stability factor, K, can be calculated from:
where \(S_{11}\), \(S_{12}\), \(S_{21}\) and \(S_{22}\) are the four scattering matrix parameters (S-parameters) that represent a complete description of the LNA at its two-ports (Pozar 2012).
The area occupation is not accurately known until the circuit layout is performed. However, it is reasonable to think that the layout area will be proportional to the sum of the areas of the individual devices (e.g., transistors, inductor and capacitors in Fig. 2). Therefore, the use of this sum as estimation of the circuit area is a valid approximation for comparison of different candidate solutions.
The inclusion of IIP3 in automated design methodologies usually takes long computation times since the IIP3 calculation involves an input power sweep. Moreover, the IIP3 calculation is difficult since linearity severely deteriorates with higher values of the input power. Therefore, selecting the best input power points to determine IIP3 is not trivial and varies for each sized circuit. The method used in this work in order to efficiently include IIP3 in the optimization process starts from the fact that IIP3 is directly related to \(P_\mathrm{DC}\). Therefore, once \(P_\mathrm{DC}\) is calculated for a given sized circuit, IIP3 can be calculated for an extrapolated input power well below \(P_\mathrm{DC}\) so that the LNA is in the linear region. We have determined that 60 dB below \(P_\mathrm{DC}\) guarantees a linear relation between input and output powers. Using this method, the computation time for IIP3 measurement is considerably reduced and it is feasible to include it within the LNA optimization loop.
2.4 Device models
RF circuit simulators are able to provide accurate values of the different performances as long as accurate compact device models are available. This is the case of transistors and capacitors, but not of inductors due to their distributed effects. An accurate evaluation of the inductor performances requires EM simulation. However, a typical EM simulation takes from few minutes up to several hours depending on the complexity of the inductor topology and the number of frequency points to analyze. Therefore, it is clearly infeasible to perform an EM simulation for each inductor of each candidate LNA solution within a circuit optimization algorithm.
As discussed in Sect. 1, reported approaches sacrifice accuracy for speed. An equivalent circuit model, e.g., the \(\uppi \)-model in Fig. 1, is used for inductors, and approximate analytical equations of the circuit parameters as a function of the inductor sizes are used. However, these models typically exhibit errors between 5 and 50% in inductance and quality factor, negatively affecting the evaluation of the LNA performances and therefore the results of the optimization process.
To solve this problem, our approach is to perform a number of EM simulations to build a global surrogate model of the inductors. With this approach, we aim at achieving a speed close to the analytical models with a much better accuracy, very close to that of EM simulation.
A first possibility could be to generate surrogate models for the different elements in the equivalent circuit model in Fig. 1. EM simulators are able to calculate the S-parameters of the inductors considered as two-ports. From these parameters, the equivalent circuit model in Fig. 1 can be approximately obtained by using some kind of regression technique. Despite this approximation error, this would be a must if only lumped circuit elements could be used in circuit simulators. However, if we take into account that modern RF circuit simulators can simulate circuits in which some elements are characterized with frequency-dependent two-ports, it is much more convenient to directly use the matrix of S-parameters in the circuit simulation. Therefore, surrogate models of the S-parameters will be used in our proposed optimization approach.
3 Surrogate modeling of inductor S-parameters
Surrogate modeling is an engineering technique used when the performances of a given system cannot be easily measured. Surrogate models represent the behavior of any given system as closely as possible while being computationally cheap to evaluate. A model is built by acquiring the behavior of a system from a limited number of smartly chosen data points. In this section, the generation of the surrogate model is discussed.
Generating a surrogate model usually involves four steps:
-
(1)
Design of experiments
The objective of surrogate models is to emulate the output response of a given system. Therefore, the model has to learn how the system responds to a given input. So, the first step in generating surrogate models is to select the samples from which the model is going to learn. These samples should cover the design space of interest, so that the model is accurate over such space.
In order to perform this sampling, a wide variety of techniques are available, from the classical Monte Carlo (MC) sampling to quasi-Monte Carlo (QMC) or Latin hypercube sampling (LHS) (Gorissen et al. 2010; McKay et al. 2000). MC relies on pure randomness; therefore, it can be inefficient. The sampling might end up with some points clustered closely, while other intervals within the design space do not have any sample.
On the other hand, LHS aims at spreading the sample points more evenly across all possible values (Aho and Hopcroft 1974). It partitions each input distribution into a number of intervals of equal probability and selects one sample from each interval.
In contrast to MC and LHS which use standard pseudo-randomness sequences, there are techniques based on low-discrepancy sequences (LDS) (Glasserman 2004), which generate deterministic sequences with no random component. These sequences are generated by following some rigorous notion of uniform coverage of the sampling space. QMC techniques employ these deterministic sequences instead of the random ones, which allow more uniform samplings (Singhee and Rutenbar 2010). Therefore, in this work QMC is used.
-
(2)
Accurate (expensive) evaluation
It is easy to understand that the model accuracy depends directly from the correct and accurate evaluation of the previously generated samples. Since the model learns from these samples, a computationally expensive simulation is used to evaluate the performances of the samples selected in the previous step. These accurate evaluations are EM simulations, which are performed with Keysight ADS Momentum Simulator (ADS Momentum).
-
(3)
Model construction
It concerns the core functions used to build a surrogate model. In this work Kriging models are used. Basically, Kriging is an interpolation method for which the interpolated values are modeled by a Gaussian process. Kriging models have been employed in several circuits and system applications, such as the modeling of the input referred noise and admittance matrix elements of a low-noise amplifier (Gorissen et al. 2008). These types of models are good candidates for the modeling of integrated inductors, due to their ability to produce smooth approximations from discrete data. One of the advantages of this core function is that, together with the predicted value for a new input sample, an estimation of the mean square error is also given, which gives an insight into the real or relative error of the model with respect to the accurate evaluation.
A clear overview of Kriging models and further mathematical properties are explained in Kleijnen (2009). The Kriging functions used in this work are applied using the Hooke–Jeeves method in the MATLAB toolbox DACE (Design and Analysis of Computer Experiments) (DACE toolbox).
-
(4)
Model Validation
Apart from the samples used to generate the model, another set of points must be generated in order to validate the model. Again, these samples were generated using QMC.
In order to introduce the strategy used to construct the model and the input parameters used, the design parameters of inductors must first be reviewed. In Fig. 4, an octagonal asymmetric inductor is presented.
The geometry of this planar spiral inductor is usually defined by four geometric parameters: number of turns (N), the inner diameter (\(D_\mathrm{in}\)), the turn width (W) and the spacing between turns (S). The modeled design space will vary in terms of N, \(D_\mathrm{in}\) and W. The number of turns varies from 1 to 8, the inner diameter between 10 and \(300\,\upmu \hbox {m}\), and the turn width between 5 (the minimum allowed by the 0.35-\(\upmu \hbox {m}\) CMOS technology used) and \(25\,\upmu \hbox {m}\). The inductor area was limited to a maximum square of \(400\,\upmu \hbox {m}\times 400\,\upmu \hbox {m}\) (a reasonable limit for any practical application). The spacing is fixed to \(2.5\,\upmu \hbox {m}\), the minimum allowed by the technology, since no performance improvement is found with larger spacing. Inner diameter and turn width are forced to fit in a grid of \(0.05\,\upmu \hbox {m}\) due to fabrication technology constraints, and for the number of turns only integers are considered due to restrictions of the parameterized layout cell used for EM simulations. For an accurate modeling, the designer must guarantee that the design space is evenly covered with training points. This is achieved by using advanced sampling techniques such as QMC. However, in design space areas such as the upper and lower bounds (design space corners), there are no training samples around each direction. Therefore, in order to achieve good accuracy along the entire design space and also the corners, 800 inductors were sampled using the QMC strategy and another 32 samples (4 corners for each inductor turn) were generated. The 832 samples used to build the model will be referred to as training inductors. For model validation, a set of 240 inductors covering the same design space was also generated using QMC. The inductors in this set will be referred to as test inductors.
In order to build a more accurate model, several surrogate models were created, one for each number of turns (e.g., one model for inductors with two turns, another for inductors with three turns, etc.). Several different strategies were considered for the accurate modeling of integrated inductors (Passos et al. 2015). However, the most accurate strategy is based on exploiting the typical inductor behavior, shown for illustration in Fig. 5.
An important parameter in the plots of inductance and quality factor in Fig. 5 is the self-resonance frequency (SRF). The SRF is the frequency at which the inductance and quality factor become 0. At this frequency, the inductor behavior becomes capacitive; hence, inductors with SRF around the working frequency should be avoided. As shown in Fig. 5, the inductor behavior changes abruptly around the SRF. Many training inductors may have their SRF around or even below the working frequency. These inductors are useless for those working frequencies; however, they strongly affect the accuracy of the surrogate models for inductors with SRF well above the working frequency.
The strategy applied to increase the model accuracy consists in creating the models based on a two-step method, as illustrated in Fig. 6. The main idea is to first build a self-resonance frequency (SRF) model using all training inductors (832 inductors). Afterward, in order to build the S-parameter models, only inductors whose SRF is sufficiently above the frequency of interest are used. For example, if the working frequency is 2.5 GHz, only inductors with \(\hbox {SRF}>3\ \hbox {GHz}\) are used to generate the S-parameter models.
The mean relative errors for the different SRF models (one per each number of turns) evaluated with the 240 test inductors are given in Table 1. The model presents a maximum mean relative error of 1.79% for the prediction of the SRF. This accuracy is quite good although it is not very critical since the role of the SRF model is just to discriminate those candidate inductors whose SRF is not high enough. Hence, with this model, whenever a candidate inductor is going to be evaluated, its SRF value is predicted. If the predicted SRF is below 3 GHz, the inductor is discarded and it is not further evaluated. Therefore, if we discard some inductors, the number of inductors in the training and test sets for the second step will be lower. If a working frequency of 2.5 GHz is selected, the number of training and test inductors for the second step is reduced to 696 and 202, respectively. The second step generates surrogate models for real and imaginary parts of all S-parameters using only these 696 inductors. In Table 2, results for this strategy are summarized for a working frequency of 2.5 GHz for each surrogate model created (one per each number of turns and for each S-parameter component) using the 202 test inductors. The mean relative errors for each one of the surrogate models presented in Table 2 show what may be perceived as relatively high errors (e.g., 1.89%). However, the large percentage errors are due to the small values of some S-parameter components, which translates into relatively high percentages. Nevertheless, when all S-parameter components are combined in order to get the inductance (L) and quality factor (Q) of a given inductor, this model shows errors always below 1%, as the last two columns in Table 2 show.
It is interesting to notice that generating an independent model for each number of turns and using the proposed two-step approach is much more accurate and more efficient than using a single model (N is an input to the model) and no inductor filtering according to the value of the SRF. Under these conditions, the average relative errors in Table 3 are obtained. It can be observed that these errors are too large, comparable to equivalent circuits using analytical models. Moreover, the generation of the Kriging model for different numbers of turns just takes 0.57s per frequency point, whereas the generation of a single model takes 28.97s, much more than the generation of 8 models for inductors with a single number of turns.
4 Experimental results
This section illustrates the application of this methodology to single- and multi-objective optimizations of low-noise amplifiers. Once fully sized circuits are obtained, two circuit simulations with SpectreRF are performed: one modeling the inductors with their S-parameters as provided by the surrogate model and another one with the S-parameters of the same inductors as provided by the EM simulator. Hence, in this way it will be possible to evaluate the accuracy of the model and its effect on the optimization results by inspecting the deviation of the performances in both simulations.
The optimizations were performed for the LNA topology shown in Fig. 2 in a 0.35-\(\upmu \hbox {m}\) CMOS technology intended to operate at the frequency band of 2.4–2.5 GHz, with a supply voltage of \(V_\mathrm{dd}=1.5\hbox {V}\). The methodology itself is independent of the fabrication technology and the LNA topology and only requires as user inputs:
-
1.
The desired specifications (optimization objectives and constraints)
-
2.
Design variables (e.g., transistors widths and lengths)
In order to understand the advantages of using a highly accurate inductor model, such as the surrogate model discussed above, it will be compared with optimizations performed using the well-known analytical \(\uppi \)-model (Yue and Wong 2000). By doing so, it will be possible to check that the accuracy of the models used to design the passive components highly influences the design of the RF block.
4.1 Single-objective optimization using PSO and GA
The first test example uses the PSO and the GA to minimize the area of the LNA. The LNA design variables are shown in Tables 4 and 5. In Table 4, \(w_{Mx}\) are the width of gates in each transistor, \(l_{Mx}\) are the channel lengths of the transistors, \(V_\mathrm{b}\) is the bias voltage, and \(C_{x}\) represent the three square capacitances used in the topology. In Table 5, the design variables for each inductor are shown, which together with those in Table 4 make a total number of 18 design variables. The design constraints and objective of the optimization are shown in the first two columns in Table 6. In addition, the inductors are subject to several constraints in order to guarantee their proper behavior in the working frequency band under unavoidable manufacturing variations. These constraints are:
where \(L_{@\mathrm{WF}}\) and \(Q_{@ \mathrm{WF}}\) are the inductance and quality factor at the working frequency, respectively (González-Echevarría et al. 2014). The inductance and quality factor at any frequency can be easily obtained from the S-parameters (Okada and Masu 2010).
Two optimizations with PSO were performed using 1000 generations and 40 particles, one using the surrogate model to evaluate the inductor S-parameters and another one using the inductor \(\uppi \)-model. The LNA performances obtained with both methods are given in the third and sixth columns in Table 6, and the values of the circuit elements are shown in Table 7.
By using these models instead of EM simulation to evaluate the inductor performances, some error in the LNA performances can be expected due to the limited model accuracy. Therefore, the inductors obtained from the LNA optimization (with both methods) were simulated electromagnetically and the simulations of the final LNAs were performed again using this more accurate evaluation of the inductor performances. The performance shifts can be observed in the fourth and seventh columns in Table 6. It can be observed that the LNA performance shifts are negligible (less than 1%) when the global surrogate model developed herein is used. However, when the analytical \(\uppi \)-model is used, huge shifts are observed (up to 65% in this experiment). In some cases, by using the \(\uppi \)-model, some of the design constraints are no longer met when the inductors are electromagnetically simulated and the design is therefore not valid (e.g., NF in column 7 in Table 6).
A similar experiment was performed with the GA to discard a significant influence of the type of optimization algorithm. For a fair comparison, we kept constant the total number of model evaluations (40,000), but used a different number of individuals (400) and generations (100). The motivation is that PSO performs better with smaller sets of solutions (particles or individuals) and a larger number of iterations. The LNA performances obtained with both methods, their deviations when inductors are electromagnetically simulated and the values of the circuit elements are shown in Tables 8 and 9, respectively.
Similarly to the previous example with PSO, in the experiments with GA it can be observed that the LNA performance shifts are negligible (less than 1%) when the global surrogate model developed herein is used. However, when the analytical \(\uppi \)-model is used, huge shifts are observed (up to 67% in the experiment shown in Table 8). In some cases, by using the \(\uppi \)-model, some of the design constraints are no longer met when the inductors are electromagnetically simulated and the design is therefore not valid (e.g., \(S_{11}\) in column 7 in Table 8).
As the optimization algorithms are stochastic, both the PSO and GA were executed five times. The results of the statistical analysis for the design objective are given in Tables 10 and 11, respectively. When the results of all these executions are simulated again with electromagnetically simulated inductors, it is found that design constraints are violated 4 times when the \(\uppi \)-model was used for the optimization (for the experiments with PSO and GA), whereas there is no violation when the surrogate model was used (for the experiments with PSO and GA).
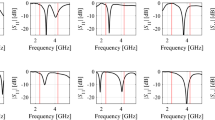
For the sake of illustration, graphical plots were performed with the circuit simulator SpectreRF for the LNAs obtained using the surrogate model of the inductors. Two simulations were performed: one using the S-parameters of the inductors obtained by the models and another with the S-parameters of the same inductors but electromagnetically simulated. Figure 7 shows the comparisons for the gain, the input and output matching and the noise figure for the experiment in Table 7. Again, it is possible to realize that the inductor surrogate model is highly accurate since the performance curves of the LNA are completely overlapped.
The time needed for the LNA optimization in a two 6-core Intel® Xeon® E5-2630 v2 processors at 2.60 GHz is 0.30 and 3.75 h CPU time for the example using the \(\uppi \)-model and the surrogate model, respectively. By using the analytical model a greater efficiency is obtained; however, it has a large disadvantage due to the huge performance shifts obtained when this model is used. As discussed above, the accuracy using the surrogate model is comparable to using EM simulations of the inductors. However, if we take into account that the EM simulation of a single inductor typically takes from a few minutes to several hours (let us assume a conservative average of 10 min per inductor), this means that the optimization process described above would need 9 months (\(40 \times 1000\times 10\) min) only to electromagnetically evaluate the inductor performances. (Obviously, this time can be decreased by using parallelization.) Therefore, the relevance of obtaining practically the same results in less than 4 h can be understood.
4.2 Multi-objective optimization using NSGA-II
In this section, the LNA performance trade-offs are explored by using a multi-objective optimization algorithm and the surrogate model to represent the inductors. As a first example, we will define an optimization which has three objectives: maximization of gain and minimization of area and power consumption. The design objectives and constraints for this optimization are given in Table 12. The optimization was performed with 1000 individuals and 300 generations. The POF obtained is shown in Fig. 8.
As a second example an optimization where the maximization of gain and the minimization of noise figure and power consumption was performed. The design specifications and constraints for this optimization are given in Table 13. The optimization was performed with 1000 individuals and 300 generations. The POF obtained is shown in Fig. 9.
In order to compare the advantages of using an accurate surrogate model instead of the analytical \(\uppi \)-model, a multi-objective optimization was performed with the \(\uppi \)-model as inductor evaluator. The optimization was performed with the same objectives, specifications and constraints as the example presented in Table 13. In Fig. 10, a comparison between the POF obtained with the surrogate and the \(\uppi \)-model is presented.
Furthermore, it is expected that a shift in the LNA performances may occur due to the usage of the models. Therefore, the inductors used in the LNAs were EM simulated and the LNAs were re-simulated in order to observe how the performances shift. In Figs. 11 and 12 it is possible to observe the new LNA POF with the inductors EM simulated for the surrogate model and the \(\uppi \)-model, respectively.
It is shown in Fig. 11 that the shifts in the POF obtained with the surrogate are negligible, whereas the shifts obtained when the \(\uppi \)-model is used are much more noticeable. Furthermore, all the LNAs obtained using the surrogate model still meet the design constraints after the inductors are electromagnetically simulated. On the contrary, only 129 out of the 1000 LNAs in the POF obtained with the \(\uppi \)-model meet the constraints after EM simulation of the inductors and re-evaluation of the LNA performances (see Fig. 13).
In order to properly compare the POFs, some comparison metrics must be used and a statistical study should be performed. Among the several metrics available in the literature, coverage set and hypervolume will be used in this paper (Zitzler and Thiele 1999). The hypervolume is calculated as the sum of the hypercubes determined by each point of the approximated POF and a reference point. As our goal is to compare the POFs generated with two different techniques and the hypervolume metric depends on the selected reference point, the same reference point is used in both cases. The hypervolume accounts for convergence and diversity of the Pareto front. The coverage set CS (A,B) between two fronts, A and B, accounts for the percentage of solutions in B that are dominated by at least one solution in A. Since the optimization times are relatively high the number of runs was limited to five. Table 14 shows the statistical results of hypervolume of the fronts obtained using the surrogate model and the \({\varvec{\uppi }}\)-model after EM simulation of the final inductors, so that the accuracy of the simulations is comparable. It can be observed that the hypervolume using the surrogate model is consistently larger. Furthermore, Table 14 also shows the coverage set between the couple of fronts: that obtained with the \(\uppi \)-model for the inductor and that obtained with the surrogate model. It can be observed that most solutions of the POF obtained with the \(\uppi \)-model are dominated by the POF obtained with the surrogate model, whereas very few solutions using the surrogate model are dominated by those using the \(\uppi \)-model.
The time needed for the LNA optimization with NSGA-II in a two 6-core Intel® Xeon® E5-2630 v2 processors at 2.60 GHz is 31.93 h CPU time using the surrogate model and 6.05 h CPU time using the \(\uppi \)-model. As in PSO, a greater efficiency is obtained by using the \(\uppi \)-model; however, huge performance shifts are obtained. However, the surrogate model provides an excellent accuracy, comparable to EM simulation, whereas the latter one would be computationally unaffordable.
5 Conclusions
In this work a highly accurate surrogate modeling strategy was presented that accurately models the S-parameters of integrated inductors. This model was successfully included in an automated design flow for the design of RF blocks and demonstrated with the single-objective and multi-objective optimization of a low-noise amplifier. By using this surrogate modeling strategy, the performance deviations at the optimized low-noise amplifiers are negligible when compared against EM simulations.
References
Aho AV, Hopcroft JE (1974) The design and analysis of computer algorithms. Addison-Wesley Longman publishing Co, Boston
Alpaydin G, Balkir S, Dundar G (2003) An evolutionary approach to automatic synthesis of high-performance analog integrated circuits. IEEE Trans Evol Comput 7:240–252. https://doi.org/10.1109/TEVC.2003.808914
Ballicchia M, Orcioni S (2010) Design and modeling of optimum quality spiral inductors with regularization and Debye approximation. IEEE Trans Comput Aided Des Integr Circuits Syst 29:1669–1681. https://doi.org/10.1109/TCAD.2010.2061470
Deb K (2010) An efficient constraint handling method for genetic algorithms. Comput Methods Appl Mech Eng 186:311–338. https://doi.org/10.1016/S0045-7825(99)00389-8
Deb K, Pratap A, Agarwal S, Meyarivan T (2002) A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans Evol Comput 6:182–197. https://doi.org/10.1109/4235.996017
Emmerich MTM, Giannakoglou KC, Naujoks B (2006) Single-and multiobjective evolutionary optimization assisted by Gaussian random field metamodels. IEEE Trans Evol Comput 10:421–439. https://doi.org/10.1109/TEVC.2005.859463
Fakhfakh M, Tlelo-Cuautle E, Siarry P (2005) Computational intelligence in analog and mixed-signal (AMS) and radio-frequency (RF) circuit design. Springer, Berlin
Glasserman P (2004) Monte Carlo methods in financial engineering. Springer, Berlin
González-Echevarría R, Castro-López R, Roca E, Fernández FV, Sieiro J, Vidal N, López-Villegas JM (2014) Automated generation of the optimal performance trade-offs of integrated inductors. IEEE Trans Comput Aided Des Integr Circuits Syst 33:1269–1273. https://doi.org/10.1109/TCAD.2014.2316092
Gorissen D, Tommasi LD, Hendrickx W, Croon J, Dhaene T (2008) RF circuit block modeling via Kriging surrogates. Paper presented at the 7th conference on microwaves, radar and wireless communications
Gorissen D, Couckuyt I, Demeester P, Dhaene T, Crombecq K (2010) A Surrogate modeling and adaptive sampling toolbox for computer based design. J Mach Learn Res 11:1051–2055
Jones DR, Schonlau M, Welch WJ (1998) Efficient global optimization of expensive black-box functions. J Glob Optim 13:455–492. https://doi.org/10.1023/A:1008306431147
Kennedy J, Eberhart R (1995) Particle swarm optimization. In: Proceedings of IEEE international conference on neural networks, Nov/Dec 1995, vol 1944, pp 1942–1948. https://doi.org/10.1109/ICNN.1995.488968
Khalesian M, Delavar MR (2016) Wireless sensors deployment optimization using a constrained Pareto-based multi-objective evolutionary approach. Eng Appl Artif Intell 53:126–139
Kleijnen JPC (2009) Kriging metamodeling in simulation: a review. Eur J Oper Res 192:707–716
Knowles J (2006) ParEGO: a hybrid algorithm with on-line landscape approximation for expensive multiobjective optimization problems. IEEE Trans Evol Comput 10:50–66. https://doi.org/10.1109/TEVC.2005.851274
Liu B, Zhao D, Reynaert P, Gielen GGE (2011) Synthesis of integrated passive components for high-frequency RF ICs based on evolutionary computation and machine learning techniques. IEEE Trans Comput Aided Des Integr Circuits Syst 30:1458–1468. https://doi.org/10.1109/TCAD.2011.2162067
Liu B, Gielen GE, Fernández FV (2014a) Automated design of analog and high-frequency circuits. Studies in computational intelligence. Springer, Berlin
Liu B, Zhao D, Reynaert P, Gielen GGE (2014b) GASPAD: a general and efficient mm-wave integrated circuit synthesis method based on surrogate model assisted evolutionary algorithm. IEEE Trans Comput Aided Des Integr Circuits Syst 33:169–182. https://doi.org/10.1109/TCAD.2013.2284109
Mandal SK, Sural S, Patra A (2008) ANN- and PSO-based synthesis of on-chip spiral inductors for RF ICs. IEEE Trans Comput Aided Des Integr Circuits Syst 27:188–192. https://doi.org/10.1109/TCAD.2007.907284
McKay MD, Beckman RJ, Conover WJ (2000) A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 42:56–61
Mitchell M (1996) An introduction to genetic algorithms. MIT Press, Cambridge
Nieuwoudt A, Ragheb T, Massoud Y (2007a) Hierarchical optimization methodology for wideband low noise amplifiers. In: 2007 Asia and South Pacific design automation conference, 23–26 Jan 2007, pp 68–73. https://doi.org/10.1109/ASPDAC.2007.357794
Nieuwoudt A, Ragheb T, Massoud Y (2007b) Narrow-band low-noise amplifier synthesis for high-performance system-on-chip design. Microelectron J 38:1123–1134. https://doi.org/10.1016/j.mejo.2007.08.007
Okada K, Masu K (2010) Modeling of spiral inductors. In: Advanced microwave circuits and systems. InTech, Rijeka, pp 292–312
Paenke I, Branke J, Yaochu J (2006) Efficient search for robust solutions by means of evolutionary algorithms and fitness approximation. IEEE Trans Evol Comput 10:405–420. https://doi.org/10.1109/TEVC.2005.859465
Passos F et al (2015) Physical vs. surrogate models of passive RF devices. In: 2015 IEEE international symposium on circuits and systems (ISCAS), 24–27 May 2015, pp 117–120. https://doi.org/10.1109/ISCAS.2015.7168584
Patanè A, Santoro A, Conca P, Caparezza G, Magna AL, Romano V, Nicosia G (2016) Multi-objective optimization and analysis for the design space exploration of analog circuits and solar cells. Eng Appl Artif Intell. https://doi.org/10.1016/j.engappai.2016.08.010
Póvoa R, Bastos I, Lourenço N, Horta N (2016) Automatic synthesis of RF front-end blocks using multi-objective evolutionary techniques. Integr VLSI J 52:243–252
Pozar DM (2012) Microwave engineering, 4th edn. Wiley, New York
Ranter CD, Plas GVd, Steyaert MSJ, Gielen GGE, Sansen WMC (2002) CYCLONE: automated design and layout of RF LC-oscillators. IEEE Trans Comput Aided Des Integr Circuits Syst 21:1161–1170. https://doi.org/10.1109/TCAD.2002.802267
Shaeffer DK, Lee TH (1997) A 1.5-V, 1.5-GHz CMOS low noise amplifier. IEEE J Solid State Circuits 32:745–759. https://doi.org/10.1109/4.568846
Shayeghi H, Hashemi Y (2015) Application of fuzzy decision-making based on INSGA-II to designing PV-wind hybrid system. Eng Appl Artif Intell 45:1–17
Singhee A, Rutenbar RA (2010) Why quasi-monte carlo is better than monte carlo or latin hypercube sampling for statistical circuit analysis. IEEE Trans Comput Aided Des Integr Circuits Syst 29:1763–1776. https://doi.org/10.1109/TCAD.2010.2062750
Tulunay G, Balkir S (2008) A synthesis tool for CMOS RF low-noise amplifiers. IEEE Trans Comput Aided Des Integr Circuits Syst 27:977–982. https://doi.org/10.1109/TCAD.2008.917579
Vancorenland P, Ranter CD, Steyaert M, Gielen G (2000) Optimal RF design using smart evolutionary algorithms. In: Proceedings 37th design automation conference, 5–9 June 2000, pp 7–10. https://doi.org/10.1145/337292.337299
Xu Y, Hsiung KL, Li X, Pileggi LT, Boyd SP (2009) Regular analog/RF integrated circuits design using optimization with recourse including ellipsoidal uncertainty. IEEE Trans Comput Aided Des Integr Circuits Syst 28:623–637. https://doi.org/10.1109/TCAD.2009.2013996
Yue CP, Wong SS (2000) Physical modeling of spiral inductors on silicon. IEEE Trans Electron Devices 47:560–568. https://doi.org/10.1109/16.824729
Zhang Q, Liu W, Tsang E, Virginas B (2010) Expensive multiobjective optimization by MOEA/D with gaussian process model. IEEE Trans Evol Comput 14:456–474. https://doi.org/10.1109/TEVC.2009.2033671
Zitzler E, Thiele L (1999) Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach. IEEE Trans Evol Comput 3:257–271. https://doi.org/10.1109/4235.797969
Web References
DACE toolbox. http://www.imm.dtu.dk/projects/dace. Accessed Feb 2017
Momentum ADS Momentum. http://www.keysight.com/en/pc-1887116/momentum-3d-planar-em-simulator?cc=ES&lc=eng. Accessed Feb 2017
Cadence Cadence SpectreRF circuit simulator. https://www.cadence.com/content/cadence-www/global/en_US/home/tools/custom-ic-analog-rf-design/circuit-simulation/spectre-rf-option.html. Accessed Feb 2017
Acknowledgements
This work was supported in part by the TEC2013-45638-C3-3-R and TEC2016-75151-C3-3-R Projects (funded by the Spanish Ministry of Economy, Industry and Competitiveness and ERDF) and in part by the P12-TIC-1481 Project (funded by Junta de Andalucia).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
All authors declare that they have no conflict of interest.
Human and animal participants
This article does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Communicated by V. Loia.
Rights and permissions
About this article
Cite this article
Passos, F., González-Echevarría, R., Roca, E. et al. A two-step surrogate modeling strategy for single-objective and multi-objective optimization of radiofrequency circuits. Soft Comput 23, 4911–4925 (2019). https://doi.org/10.1007/s00500-018-3150-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-018-3150-9