Dynamical Complexity of a Ratio-Dependent Predator-Prey Model with Strong Additive Allee Effect

Abstract

In this paper, a predator-prey systems of two species is proposed where prey population is subjected to a strong additive Allee effect and predator population consumes the prey according to the ratio-dependent Holling type-II functional response. We use the blow-up technique in order to explore the local structure of orbits in the vicinity of origin. We have determined the conditions for extinction/survival scenarios of species. Some basic dynamical results; the stability; phenomenon of bi-stability and the existence of separatrix curves; Hopf bifurcation; saddle-node bifurcation; homoclinic bifurcation, and Bogdanov-Takens bifurcation of the system are studied. Numerical simulation results that complement the theoretical predictions are presented. A discussion of the consequences of additive Allee effect on the model along with the ecological implications of the analytic and numerical findings is presented.

29.1 Introduction

The modeling of predator-prey interactions incorporating Allee effect [2, 3, 11] in prey population growth has become a broad field of research in ecology for the understanding of population dynamics. The originator and namesake of Allee effect was Warder Clyde Allee (1885–1955), an US zoologist and ecologist, who observed that many animal and plant species suffer a decrease of the per capita rate of increase as their populations reach small sizes or low densities. In particular, the population exhibits a “critical size or density,” below which the per capita growth rate is negative and the population declines on average, and above which the per capita growth rate is positive and the population increases on average yielding convergence to the carrying capacity. This ecological phenomenon is termed as strong Allee effect. The Allee effect can be caused by difficulties in finding mating partners for sexual reproduction at small densities, inbreeding depression, demographic stochasticity, or a reduction in cooperative interactions.

Several algebraic forms to describe the Allee effect are available in the literature, see Table 1 of [2] or Table 3.1 of [3]. In this present study, we consider the equation

$$\begin{aligned} \frac{dx}{dt} = x\left[ r(1-\frac{x}{K})-\frac{m}{x+b}\right] \end{aligned}$$

(29.1)

which is commonly known as an additive Allee effect, where K is the carrying capacity, r denotes the intrinsic per capita growth rate of the population, m and b are the Allee effect constants such that $K>b$. The term subtracted from the logistic growth term is proportional to $\frac{m}{x+b}$ in Eq. (29.1) is to represent the reduction of the per capita growth rate of a population due to Allee effect.

We have considered the ratio-dependent functional response where the consumption rate of the predator is a function of the prey-to-predator ratio, not on the absolute numbers of prey only or both species. There are growing explicit biological and physiological evidence (cf. [1, 6]) that in many situations when predators have to search for food (and, therefore, have to share or compete for food), a more suitable general predator-prey theory should be based on the ratio-dependent theory. To the best of our knowledge, the effect of additive Allee on a ratio-dependent [5–7, 12, 13] predator-prey model is entirely unaddressed in the literature to date. However, the effect of multiplicative Allee effect (with single and multiple mechanism) on ratio-dependent predator-prey model have recently been described in [4, 9]. In this paper, we offer a contribution toward addressing this major research gap by establishing complete study of the dynamics including a detailed bifurcation analysis of our proposed model.

This paper is organized as follows: The model is proposed in Sect. 29.2 along with some basic results. Section 29.3 deals with the mathematical analysis including existence of equilibria, stability, and Hopf bifurcation analysis of the model. This section also discusses the stability analysis of the origin (a complicated equilibrium point). In Sect. 29.4, we prove the existence of a Bogdanov-Takens bifurcation of co-dimension 2 including a series of other bifurcations, such as saddle-node bifurcation, Hopf bifurcation, and Homoclinic bifurcations. In Sect. 29.5, we perform numerical simulation in support of our analytical results and discuss the main results of the paper.

29.2 Model Description and Basic Results

In this paper, we consider a predator-prey model where the prey growth is damped by the strong additive Allee effect given by Eq. (29.1) and the functional response of predator to prey abundance is ratio-dependent given by $\frac{c x}{x+\vartheta y}$ where c is the capturing rate of the predator and $\vartheta$ is the half-saturation constant of the predator functional response. Accordingly, we are concerned with the following ratio-dependent Holling-type II predator-prey model

$$\begin{aligned} \frac{dx}{dt}= & {} \left[ r \left( 1-\frac{x}{K}\right) -\frac{m}{x+b}\right] x- \frac{c xy}{x+\vartheta y},\end{aligned}$$

(29.2a)

$$\begin{aligned} \frac{dy}{dt}= & {} \frac{c_1 xy}{x+\vartheta y}-d y. \end{aligned}$$

(29.2b)

such that $x(0)>0$, $y(0)>0$. In system (29.2), x(t) and y(t) stands for prey and predator density at time t, and $c_1$, d are positive constants that stand for conversion rate of prey into predators biomass, death rate of predator, respectively.

Fig. 29.1

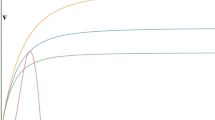
Blue curve Strong Allee effect for $\gamma >\rho$, $\rho <1$ and $(\rho +1)^2>4\gamma$. The parameter values are $\alpha =0.3$, $\gamma =0.25$, $\delta =0.5$, $\rho =0.2$. Red curve Weak Allee effect for $\gamma <\rho$. Parameter values are $\alpha =0.3$, $\gamma =0.25$, $\delta =0.5$, $\rho =0.3$

Non-dimensionalization of this model (29.2) can be performed by using the transformation $x=K\widehat{x}$, $y=\frac{K}{\vartheta }\widehat{y}$, $t=\frac{\widehat{t}}{r}$ and dropping the hats for notational convenience, we derive

$$\begin{aligned} \frac{dx}{dt}= & {} x(1-x)-\frac{\gamma x}{x+\rho }-\frac{\alpha xy}{x+y}=f(x, y), \end{aligned}$$

(29.3a)

$$\begin{aligned} \frac{dy}{dt}= & {} \frac{\beta xy}{x+y}-\delta y=g(x, y) , \end{aligned}$$

(29.3b)

where $\alpha =\frac{c}{r\vartheta }$, $\beta =\frac{c_1}{r}$, $\gamma =\frac{m}{r}$, $\rho =\frac{b}{K}$ and $\delta =\frac{d}{r}$ are the dimensionless parameters with the following initial conditions

$$\begin{aligned} x(0)=x_0>0, ~~y(0)=y_0>0. \nonumber \end{aligned}$$

The model system (29.3) is not well-defined at the origin and for this we define $f(0,0)=g(0,0)=0$. To illustrate the types of Allee effect (cf. [10]) on the prey population in the absence of predator, we present Fig. 29.1. In this study, we only consider strong Allee effect on the prey population and we aim to discuss the complex interplay between the strong additive Allee effect and the predation on the deterministic population dynamics in continuous time. For strong Allee effect, we have $\gamma >\rho$, $\rho <1$ and $(\rho +1)^2>4\gamma$. Based on the standard methods we shall present some preliminary results like positivity and the boundedness of solutions of the system (29.3) for the case of a strong Allee effect without proof.

Lemma 29.1

Solutions of model (29.3) corresponding to initial conditions (29.4) are defined on $[0,+ \infty )$ and remain positive for all $t\ge 0$.

Theorem 29.1

All the solutions of system (29.3) that initiate in $R^2_+$ are uniformly bounded with an ultimate bound.

29.3 Stability and Hopf Bifurcation Results

We now find all biological feasible equilibria admitted by system (29.3). For all parameter values, (0, 0) is an equilibrium point (controversial equilibrium point) of the system. The equilibria on the positive x-axis are $E_1(x_1, 0)$ and $E_2(x_2, 0)$ where

$$ x_1=\frac{1-\rho -\sqrt{D_1}}{2} \ \text {and}\ x_2=\frac{1-\rho +\sqrt{D_1}}{2} $$

such that $D_1=(1+\rho )^2-4\gamma >0$. If $\gamma =\frac{1}{4}(1+\rho )^2$, both the axial equilibria collides to $\left( \frac{1}{2}(1-\rho ), 0\right)$ and if $\gamma >\frac{1}{4}(1+\rho )^2$, there exists no axial equilibria on the positive x-axis. The other equilibria, if exists, are the interior equilibrium point(s). Assume $A=(1-\rho )\beta -$ $(\beta -\delta )\alpha$, $B= \alpha \rho \,\left( \beta -\delta \right) +\beta \, \left( \gamma -\rho \right) >0$ and $D_2=A^2-4\beta B$, then we have the following three cases:

• 1. If $D_2>0$, then there exists two interior equilibrium points namely, $E_i^*\equiv (x_i^*,y_i^*)$, where $x_1^*=\frac{A-\sqrt{D_2}}{2\beta }$, $x_2^*=\frac{A+\sqrt{D_2}}{2\beta }$, $y_i^*=\frac{x_i^*\left( \beta -\delta \right) }{\delta }$, $i=1,2$ provided $A>0$ and $\beta >\delta$.

• 2. If $D_2=0$, $\beta >\delta$ and $A>0$ then the two positive equilibrium points $E_1^*$ and $E_2^*$ coincide to an unique interior equilibrium point $E^*(x^*, y^*)=\left( \frac{A}{2\beta }, \frac{A(\beta -\delta )}{2\delta \beta }\right)$.

• 3. If either $D_2<0$, or $A<0$, the system (29.3) has no interior equilibrium point (Fig. 29.2).

Fig. 29.2

Graphical illustration of nullclines. Here, the red (blue) curves represent the predator(prey) nontrivial nullclines. Equilibria are represented by small red circles. The black lines represent the vertical asymptotes that exists when the nontrivial prey nullcline become an unbounded curve. Top panel $\alpha =0.3$, $\gamma =0.25$, $\delta =0.5$, $\rho =0.2$, $\beta =0.9$ (black), 1.5 (red) and 2.5 (magenta). Middle panel $\alpha = 0.1$, $\beta =0.9$, $\gamma =0.25$, $\delta =0.5$, $\rho =0.2$. Lower panel $\alpha =0.2$, $\beta =0.9$, $\gamma =0.25$, $\delta =0.5$, $\rho =0.2$

29.3.1 Qualitative Property of Solutions Near ${\varvec{(0, 0)}}$

We note that system (29.3) is not well defined at $E_0 \equiv (0, 0)$. Thus system (29.3) cannot be linearized at (0, 0) and the standard linear stability analysis method for (0, 0) is not applicable. In Jost et al. [6] have studied the analytical behavior at (0, 0) for a common ratio-dependent model by blow-up method. Following [14], we have studied crucially all possible topological structures of a small neighborhood of (0, 0) where the trajectories approach the origin along characteristic directions. We redefine the derivative as $\frac{dx}{dt}=\frac{dy}{dt}=0$ when $(x, y)=(0, 0)$. To be compatible with ecological significance, we analyze the behavior of trajectories near $E_0 (0, 0)$ in presence of all other critical points. Through time rescaling $dt\rightarrow \left( x+\rho \right) \left( x+y\right) d\tau$, we obtain a polynomial differential equations system topologically equivalent to original one in the interior of first quadrant. We introduce polar coordinates $(r, \theta )$, setting $x=r \cos \,\theta$, $y=r \sin \,\theta$, and the polynomial differential equations system reduces to:

$$\begin{aligned} \frac{dr}{dt}&= r^2\left( H(\theta )+o(1)\right) ,\end{aligned}$$

(29.4a)

$$\begin{aligned} \frac{d\theta }{dt}&= r\left( G(\theta )+o(1)\right) , \end{aligned}$$

(29.4b)

where H and G are homogeneous trigonometric polynomials in the variables $\cos \theta$ and $\sin \theta$ such that

$$\begin{aligned} H(\theta )&= -\rho \,\delta \, \sin ^{3} \theta -\cos \theta \sin \theta ( -\rho \left( \beta -\delta \right) \,\sin \theta \\&\quad + \left( \gamma -\rho +\alpha \,\rho \right) \cos \theta ) + \left( \rho -\gamma \right) \cos ^{3}\theta , \\ G(\theta )&= \cos \theta \sin \theta (\left( \alpha \,\rho -\rho \,\delta -\rho +\gamma \right) \sin \theta \\&\quad + \left( \rho \,\beta -\rho \,\delta +\gamma -\rho \right) \cos \theta ). \end{aligned}$$

Then, the characteristic equation is given by $G(\theta )=0$, i.e.,

$$\begin{aligned} \cos \theta \sin \theta \left( \left( \alpha \,\rho -\rho \,\delta -\rho +\gamma \right) \sin \theta + \left( \rho \,\beta -\rho \,\delta +\gamma -\rho \right) \cos \theta \right) =0. \end{aligned}$$

(29.5)

By [14], any trajectory that will tends to origin must tend to it either spirally or along a fixed direction. This can be characterized from the characteristic equation. Clearly, $\rho \,\left( \beta -\delta \right) +\gamma -\rho >0$. Then, the following three cases arise:

29.3.1.1 Case 1: $\alpha \,\rho -\rho \,\delta -\rho +\gamma >0$

In this case, the characteristic equation (29.5) has two roots in $0\le \theta \le \frac{\pi }{2}$, namely $\theta _1=0$ and $\theta _2=\frac{\pi }{2}$.

Theorem 29.2

Suppose that $(\alpha \,\rho -\rho \,\delta -\rho +\gamma )>0$. Then

• 1. there exists $\varepsilon _1>0$ and $r_1>0$ such that there exists a unique orbit of the system in $\left\{ \left( \theta , r\right) : 0\le \theta <\varepsilon _1, \,\, 0<r<r_1\right\}$ tends to (0, 0) along $\theta _1=0$ as $t\rightarrow +\infty$,

• 2. there exists $\varepsilon _2>0$ and $r_2>0$ such that all orbits of the system in $\left\{ \left( \theta , r\right) : 0\le \frac{\pi }{2}-\theta <\varepsilon _2, \,\, 0<r<r_2\right\}$ that tend to (0, 0) along $\theta _2=\frac{\pi }{2}$ as $t\rightarrow +\infty$.

29.3.1.2 Case 2: $\alpha \,\rho -\rho \,\delta -\rho +\gamma =0$

In this case Eq. (29.5) has two roots in $0\le \theta \le \frac{\pi }{2}$, namely $\theta _1=0$ and $\theta _2=\frac{\pi }{2}$ with $\theta _2$ being a real multiple root of multiplicity two of $G(\theta )=0$.

Theorem 29.3

Suppose that $(\alpha \,\rho -\rho \,\delta -\rho +\gamma )=0$. Then

• 1. there exists $\varepsilon _3>0$ and $r_3>0$ such that there exists a unique orbit of the system in $\left\{ \left( \theta , r\right) : 0\le \theta <\varepsilon _3, \,\, 0<r<r_3\right\}$ tends to (0, 0) along $\theta _1=0$ as $t\rightarrow +\infty$,

• 2. there exists $\varepsilon _4>0$ and $r_4>0$ such that all orbits of the system in $\left\{ \left( \theta , r\right) : 0\le \frac{\pi }{2}-\theta <\varepsilon _4, \,\, 0<r<r_4\right\}$ that tend to (0, 0) along $\theta _2=\frac{\pi }{2}$ as $t\rightarrow +\infty$.

29.3.1.3 Case 3: $\alpha \,\rho -\rho \,\delta -\rho +\gamma <0$

In this case, (29.5) has three simple roots, namely $\theta _1=0$, $\theta _2=\frac{\pi }{2}$ and $\theta _3=\arctan \frac{-(\rho \,\beta -\rho \,\delta +\gamma -\rho )}{\alpha \,\rho -\rho \,\delta -\rho +\gamma }$. We have exactly the same results as stated in the above theorems for characteristic directions $\theta _1$ and $\theta _2$ and we have to study for the other characteristic direction $\theta _3$ only. We apply Briot-Bouquet transformation [14] to prove the following theorem.

Theorem 29.4

Suppose $(\alpha \,\rho -\rho \,\delta -\rho +\gamma )<0$. Then there exist $\varepsilon _5>0$ and $r_5>0$, such that all orbits of the system in $\left\{ \left( \theta , r\right) : 0\le |\theta -\theta _3|<\varepsilon _5, \,\, 0<r<r_5\right\}$ that tends to (0, 0) along $\theta _3$ as $t\rightarrow \infty$.

29.3.2 Local Stability of Equilibria and Bifurcation Results

In this section, we focus on investigating the local asymptotic stability of the boundary equilibria $E_1$ and $E_2$ and interior equilibria $E_i^*$, $i=1,2$, whenever they exists, by studying the eigenvalues of the Jacobian matrix evaluated at each equilibrium points. Furthermore, we also study the existence of Hopf bifurcation around the interior equilibrium point $E_2^*$ with $\alpha$ as bifurcation parameter arising when $E_2^*$ looses its stability.

$E_1(x_1, 0)$ is a saddle point having the x-axis as an unstable manifold if interior equilibria does not exits, otherwise it is an unstable node provide $\beta \ne \delta$. If $\beta =\delta$, the system (29.3) is reduced to the following system by suitable transformation

$$\begin{aligned} \dot{z}_1=\lambda _{11} z_1+||z||^2,~~ \dot{z}_2=-\frac{\beta }{x_1}\,{z_2}^{2}+||z||^3, \end{aligned}$$

where $\lambda _{11}=\frac{x_1\sqrt{D_1}}{x_1+\rho }>0$. It indicates that $E_1(x_1, 0)$ is a saddle-node (repelling).

$E_2(x_2, 0)$ is stable if interior equilibria does not exits, otherwise it is a saddle having stable manifold along x-axis provided $\beta \ne \delta$. If $\beta =\delta$, $E_2\equiv (x_2, 0)$ of system (29.3) is a saddle-node (attracting).

The trace and determinant of the Jacobian matrix $J_i^*$ of the system (29.3) at $E_i^*$ are given by

$$\begin{aligned} Tr (J_i^*)|_{(x_i^*,y_i^*)}&=-\frac{x_i^*\sqrt{D_2}}{\beta \left( x_i^*+\rho \right) }- \frac{x_i^*y_i^*(\beta -\alpha )}{\left( x_i^*+y_i^*\right) ^2} ~~ \text {and }\\ \det J_i^*|_{(x_i^*,y_i^*)}&={\frac{ \left( 2\beta x_i^*-A\right) {x_i^*}^{2}\,y_i^*}{ \left( x_i^*+\rho \right) \left( x_i^*+y_i^* \right) ^{2}}}={\frac{(-1)^i \sqrt{D_2} {x_i^*}^{2}\,y_i^*}{ \left( x_i^*+\rho \right) \left( x_i^*+y_i^* \right) ^{2}}}. \end{aligned}$$

It clearly shows that, the critical point $(x_1^*,y_1^*)$ is always a saddle point, where as, the locally asymptotic stability of the critical point $(x_2^*,y_2^*)$ is determined by sign of trace of $J_2^*|_{(x_2^*,y_2^*)}$. For $\alpha <\beta$, $Tr (J_2^*)|_{(x_2^*,y_2^*)}<0$. Therefore, the system (29.3) will be locally asymptotically stable around the interior equilibrium point $E_2^*(x_2^*,y_2^*)$ if $\alpha <\beta$.

29.3.2.1 Hopf Bifurcation and Its Degeneracy

Consider that $\exists$ $\alpha =\alpha ^*$ such that $Tr (J_2^*)|_{(x_2^*,y_2^*)}=0$. Consequently, since $\det J_2^*|_{(x_2^*,y_2^*)}>0$, both the eigenvalues of $J_2^*$ at $(x_2^*,y_2^*)$ are purely imaginary given by $\pm i \sqrt{\det J_2^*|_{(x_2^*,y_2^*,\alpha ^*)}}$. It has been observed that the transversality condition for Hopf bifurcation holds, therefore, the system experiences a Hopf bifurcation at the critical value $\alpha =\alpha ^*$. Further, $E_2^*(x_2^*,y_2^*)$ is unstable if $Tr (J_2^*)|_{(x_2^*,y_2^*)}>0$. It is to be noted that the computation of explicit expression for $\alpha ^*$ in terms of system parameters other than $\alpha$ is a very cumbersome task and is not carried out here. However, it may be observed that, whenever $\alpha < \alpha ^*$, the positive interior equilibrium $E_2^*$ of system (29.3) is a locally asymptotically stable node and for $\alpha > \alpha ^*$, $E_2^*$ is an unstable focus through a Hopf bifurcation that occurs around $E_2^*$ due to the stability changes from stable to unstable at the critical value $\alpha =\alpha ^*$. We will employ a numerical example to illustrate the fact discussed above.

Degeneracy of Hopf bifurcation point can be determined by computing Lyapunov coefficients or by deriving normal form with the help of central manifold argument. If it is nondegenerate then we have only one limit cycle around $E_2^*$ in the vicinity of $\alpha =\alpha ^*$ and if it is degenerate then we have to compute the multiplicity of the focus $E_2^*$ at $\alpha =\alpha ^*$. We have observed numerically that the first Lyapunov coefficient is positive.

29.3.2.2 Saddle-Node Bifurcation

Theorem 29.5

The system (29.3) undergoes a saddle-node bifurcation around $E^*\equiv (x^*, y^*)$ when $\rho =\rho ^*$ where $\rho ^*={\frac{-\beta +\alpha \,\beta -\alpha \,\delta +2\,\beta \,\sqrt{\gamma }}{\beta }}$ and $A=(1-\rho )\beta -(\beta -\delta )\alpha$ provided $A>0$, $\alpha \left( \beta -\delta \right) +2\,\beta \,\sqrt{\gamma }>\beta$ and $\beta >\alpha$.

Proof

One of the eigenvalues of the Jacobian matrix (${J}^*$, say) evaluated at ${E^*}({x}^*, {y}^*)$ will be zero iff $\det {J}^*|_{({x}^*, {y}^*)}=0$, which gives $\rho ={\frac{-\beta +\alpha \,\beta -\alpha \,\delta +2\,\beta \,\sqrt{\gamma }}{\beta }}=\rho ^*$, say. The other eigenvalue is given by $Tr~ (J^*)=-\frac{x_1^*y_1^*(\beta -\alpha )}{\left( x_1^*+y_1^*\right) ^2}$ which will be negative in order to ensure a saddle-node bifurcation implying $\beta >\alpha$. The eigenvectors of $J^*$ and $(J^*)^T$ associated to the eigenvalue 0 is given by $\varLambda _{21}= \left( \frac{\delta }{\alpha -\delta }, 1\right) ^T$ and $\varLambda _{22}=\left( -{\frac{\beta \, \left( \beta -\delta \right) }{\alpha \,\delta }}, 1\right) ^T$, respectively. Now, $\varLambda _{22}^T [F_\rho (E^*,\rho ^*)]={\frac{-2\, \left( \beta -\delta \right) \gamma \,A{\beta }^{2}}{\alpha \,\delta \, \left( A+2\,\rho ^*\,\beta \right) ^{2}}}\ne 0$ and $\varLambda _{22}^T[D^2F(E^*,\rho ^*) (\varLambda _{21},\varLambda _{21})]\ne 0$. Thus by using Sotomayor’s theorem, we conclude that, the system experiences a saddle-node bifurcation around $E^*$ at the bifurcation value $\rho =\rho ^*$. This means that, there are no equilibria for $\rho <\rho ^*$ and there are two equilibria namely $E_i^*\equiv (x_i^*, y_i^*)$, $i=1,2$ for $\rho >\rho ^*$, one of which is saddle point and the other is a node.

29.4 Bogdanov-Takens Bifurcation

In this section, we discuss the Bogdanov-Takens bifurcation of the model system (29.3) by using the methods in [8]. We assume that the conditions $\beta >\delta$, $A>0$, $A^2=4\beta B$ hold for which the two interior equilibria $E_1^*$ and $E_2^*$ merge into the nonhyperbolic critical point $E^*\left( \frac{A}{2\beta }, \frac{A(\beta -\delta )}{2\beta \delta }\right)$. Under these conditions it can be shown that $E^*$ is a saddle node whenever $\alpha \ne \beta$; attracting if $\beta >\alpha$ and repelling if $\beta <\alpha$. We assume $\alpha =\beta =\alpha ^*$. In this case, the Jacobian matrix corresponding to the linearization of (29.3) at $E^*$ has two zero eigenvalues. Our first task is to investigate the nature of the critical point $E^*$ under the conditions $\alpha =\beta =\alpha ^*$ and $\delta =\delta ^*$.

Using the following transformation $x_1=x-x^*$, $y_1=y-y^*$, $x^*=A/2\beta$, and $y^*=A(\beta -\delta )/2\beta \delta$, we get

$$\begin{aligned} \dot{x}_1&=\bar{p}_{10}x_1+\bar{p}_{01}x_2 + \bar{p}_{20}x_1^2 +\bar{p}_{11} x_1x_2+\bar{p}_{02}x_2^2+O(||x||^3)\end{aligned}$$

(29.6)

$$\begin{aligned} \dot{x}_2&=\bar{q}_{10}x_1+\bar{q}_{01}x_2 + \bar{q}_{20}x_1^2 +\bar{q}_{11}x_1x_2 +\bar{q}_{02}x_2^2+O(||x||^3) \end{aligned}$$

(29.7)

where $\bar{p}_{ij}=\frac{1}{i!j!}\frac{\partial ^{i+j}f}{\partial x_1^i \partial x_2^j}$, $\bar{q}_{ij}=\frac{1}{i!j!}\frac{\partial ^{i+j}g}{\partial x_1^i \partial x_2^j}$ at $E^*$ and $1 \le i+j \le 2$. Using a series of transformations, we reduce the system (29.3) to

$$\begin{aligned} \frac{d\omega _1}{dt}&=\omega _2,\end{aligned}$$

(29.8)

$$\begin{aligned} \frac{d\omega _2}{dt}&= \rho _1 \omega _1^2+\rho _2\omega _1\omega _2+O(||\omega ||^3), \end{aligned}$$

(29.9)

where $\rho _1=\bar{p}_{01}\bar{q}_{20} + \bar{p}_{10}\, \left( \bar{p}_{20}- \bar{q}_{11}\right) -{\frac{{\bar{p}_{10}}^{2} \left( \bar{p}_{11}- \bar{q}_{02}\right) }{b_1}}+ {\frac{\bar{p}_{02}\,{\bar{p}_{10}}^{3}}{{\bar{p}_{01}}^{2}}}$ and $\rho _2=- \frac{\bar{p}_{10}}{\bar{p}_{01}}(\bar{p}_{11}+2\bar{q}_{02})+2\bar{p}_{20}+\bar{q}_{11}$ when $\rho _1\rho _2\ne 0$. Hence, the critical point $E^*$ is a cusp of co-dimension 2, i.e., a Bogdanov-Takens singularity. This shows that for parameters $(\alpha , \delta )$ in a neighborhood of $(\alpha ^*, \delta ^*)$, the model system (29.3) undergoes BT bifurcation at $E^*$.

Now our task is to derive the generic normal unfolding of BT singularity. Consider $\alpha =\beta =\alpha ^*+\lambda _1$, $\delta =\delta ^*+\lambda _2$ where $\lambda _1$ and $\lambda _2$ is very small. Then in a sufficiently small neighborhood of $\left( x^*, y^*, \lambda ^*\right)$, there exists a parameter dependent nonlinear smooth invertible variable transformations, smooth invertible parameter changes, and a direction preserving time reparametrization, which together reduce the system (29.3) to the following normal form

$$\begin{aligned} \frac{d\xi _1}{d\tau }&= \xi _2,\end{aligned}$$

(29.10)

$$\begin{aligned} \frac{d\xi _2}{d\tau }&= \mu _1+\mu _2 \xi _1+\xi _1^2+s\xi _1\xi _2, \end{aligned}$$

(29.11)

where $s=\pm 1$. The expressions of $\mu _1$, $\mu _2$ and the transversality condition of a Bogdanov-Takens bifurcation are not presented here for the lack of space.

Fig. 29.3

Top panel Origin is an attractor for $\alpha =0.3$ ($(\alpha \, \rho -\rho \,\delta -\rho +\gamma )>0$), $\alpha =0.25$ ($(\alpha \,\rho -\rho \,\delta -\rho +\gamma )=0$) and $\alpha =0.2$ ($(\alpha \,\rho -\rho \,\delta -\rho +\gamma )<0$) with other parameter values $\beta =0.9$, $\gamma =0.25$, $\delta =0.5$, $\rho =0.2$. Lower panel For $\alpha =0.3$, $\beta =2.5$, $\gamma =0.25$, $\delta =0.5$, $\rho =0.2$, origin is a global attractor

Fig. 29.4

Phase portraits in the (x, y) plane. Top panel When $\lambda _1=0, \lambda _2=0$, the unique degenerate interior equilibrium point $E^*$ is a cusp of codimension 2. Middle panel When $\lambda _1=0.190685425, \lambda _2=-0.151314575$, there exists a limit cycle. Lower panel When $\lambda _1=0.200385425, \lambda _2=-0.0164314575$, there is a homoclinic orbit (shown by red solid curve). The parameter values are $\alpha =1.009314575=\beta$, $\gamma =0.08$, $\delta =0.505$, $\rho =0.07$

Assume that $s=-1$. There exists a neighborhood of $\left( \mu _1, \mu _2\right) =(0, 0)$ in $R^2$ so that the bifurcation plane is divided into four regions by the following curves

• 1. $SN^+ =\left\{ \left( \mu _1, \mu _2\right) : \mu _2^2=4\mu _1, \mu _2<0\right\}$,

• 2. $SN^- =\left\{ \left( \mu _1, \mu _2\right) : \mu _2^2=4\mu _1, \mu _2>0\right\}$,

• 3. $H =\big \{\left( \mu _1, \mu _2\right) : \mu _1=0, \mu _2<0\big \}$,

• 4. $HL =\left\{ \left( \mu _1, \mu _2\right) : \mu _1 =-\frac{6}{25}\mu _2^2+O(\mu _2^2), \mu _2<0\right\}$,

where SN represents a saddle-node bifurcation curve having two branches $SN^+$ and $SN^-$ corresponding to $\mu _2<0$ and $\mu _2>0$ respectively, H is the Hopf bifurcation curve and HL is the Homoclinic bifurcation curve. For the case $s = +1$, the local representations of bifurcation curves in a small neighborhood of $\left( \mu _1, \mu _2\right) =(0, 0)$ will be obtained by using the linear transformation of coordinates $\left( \xi _1, \xi _2, t, \mu _1, \mu _2\right) \rightarrow \left( \xi _1, -\xi _2, -t, \mu _1, -\mu _2\right)$.

29.5 Conclusion

The Allee effect has been shown to be very common in population dynamics. In this paper we have proposed a ratio-dependent predator-prey model with a strong additive Allee effect in prey population growth. We have shown that the trajectories approach the origin along characteristic directions divide a neighborhood of the origin into a finite number sectors. We have observed that the origin is always a point of attraction (cf. Fig. 29.3). For a certain set of parameters, the total extinction, population coexistence or the oscillating coexistence of population are observed. The bi-stability scenario is detected. Two singularities (0, 0) and $E^*_2$ can be local attractor at the first quadrant, or a limit cycle coexists around $E^*_2$ with a locally asymptotically stable point (0, 0). Both the basins of attractions are separated by a separatrix and the trajectories near the separatrix curve are extremely sensitive to the choice of initial condition. We have shown that the model exhibit codimension two bifurcations near a Bogdanov-Takens singularity, which produces a series of bifurcation like Hopf bifurcation, saddle-node bifurcation, Homoclinic curve when two parameters vary near the interior equilibrium point for some specific parameter values (cf. Fig. 29.4).