Keywords

1 Introduction

We use graph theory’s some important techniques to solve the problem of partitioning a community graph to minimize the number of edges or links that connect different community [1]. The aim of partitioning a community graph to sub-graphs is to detect similar vertices which form a graph and such sub-graphs can be formed. For example, considering Facebook is a very large social graph. It can be partitioned into sub-graphs, and each sub-group should belong to a particular characteristics. Such cases we require graph partitions. In this partition, it is not mandatory that each sub-group contain similar number of members. A partition of a community graph is to divide into clusters, such that each similar vertex belongs to one cluster. Here a cluster means a particular community. Based on this technique, we partition a community graph into various sub-graphs after detecting various vertices belonging to a particular community or cluster.

2 Basics in Graph Theory

Social network, its actors and the relationship between them can be represented using vertices and edges [2]. The most important parameter of a network (i.e., a digraph) is the number of vertices and arcs. Here we denote n for number of vertices and m for number of arcs. When an arc is created by using two vertices u and v, which is denoted by uv. Then the initial vertex is the u and the terminal vertex is the v in the arc uv.

2.1 Digraph

A digraph or directed graph G = (V, A) with \( V = \left\{ {V_{1} , \, V_{2} ,\, \ldots \ldots .,V_{n} } \right\} \) can be represented as adjacency matrix A. The matrix A is of order nXn where A ij is 1 or 0 depending on V i V j is an edge or not. Note that A ii  = 0 for all i.

2.2 Sub-digraph

A sub-digraph of G to be (V 1 , A 1) where \( V_{1} \; \subseteq \;V,A_{1}\, \subseteq \; A \) and if uv is an element of A 1 then u and v belong to V 1.

2.3 Adjacency Matrix

Let a graph G with n nodes or vertices \( V_{1} , \, V_{2} , \ldots .,V_{n} \) having one row and one column for each node or vertex. Then the adjacency matrix A ij of graph G is an nXn square matrix, which shows one (1) in A ij if there is an edge from V i to V j ; otherwise zero (0).

2.4 Good Partition

When a graph is divided into two sets of nodes by removing the edges that connect nodes in different sets should be minimized. While cutting the graph into two sets of nodes so that both the sets contain approximately equal number of nodes or vertices [1].

In Fig. 1 graph G 1 has seven nodes \( \left\{ {\varvec{V}_{1} , \, \varvec{V}_{2} , \, \varvec{V}_{3} , \, \varvec{V}_{4} , \, \varvec{V}_{5} , \, \varvec{V}_{6} , \, \varvec{V}_{7} } \right\} \). After cutting into two parts approximately equal in size, the first partition has nodes \( \left\{ {\varvec{V}_{1} , \, \varvec{V}_{2} , \, \varvec{V}_{3} , \, \varvec{V}_{4} } \right\} \) and the second partition has nodes \( \left\{ {\varvec{V}_{5} , \, \varvec{V}_{6} , \, \varvec{V}_{7} } \right\} \). The cut consists of only the edge \( \left( {\varvec{V}_{3} , \, \varvec{V}_{5} } \right) \) and the size of edge is 1.

Fig. 1
figure 1

Graph G 1 with seven nodes

Full size image

In Fig. 2 graph G 2 has eight nodes \( \left\{ {\varvec{V}_{1} , \, \varvec{V}_{2} , \, \varvec{V}_{3} , \, \varvec{V}_{4} , \, \varvec{V}_{5} , \, \varvec{V}_{6} , \, \varvec{V}_{7} , \, \varvec{V}_{8} } \right\} \). Here two edges, \( \left( {\varvec{V}_{3} , \, \varvec{V}_{7} } \right) \) and \( \left( {\varvec{V}_{2} , \, \varvec{V}_{6} } \right) \) are used to cut the graph into two parts of equal size rather than cutting at the edge \( \left( {\varvec{V}_{5} , \, \varvec{V}_{8} } \right) \). The partition at the edge \( \left( {\varvec{V}_{5} , \, \varvec{V}_{8} } \right) \) is too small. So we reject the cut and choose the best one for cut consisting of edges \( \left( {\varvec{V}_{2} , \, \varvec{V}_{6} } \right) \) and \( \left( {\varvec{V}_{3} , \, \varvec{V}_{7} } \right) \), which partitions the graph into two equal sets of nodes \( \left\{ {\varvec{V}_{1} , \, \varvec{V}_{2} , \, \varvec{V}_{3} , \, \varvec{V}_{4} } \right\} \) and \( \left\{ {\varvec{V}_{5} , \, \varvec{V}_{6} , \, \varvec{V}_{7} , \, \varvec{V}_{8} } \right\} \).

Fig. 2
figure 2

Graph G 2 with eight nodes

Full size image

2.5 Normalized Cuts

A good cut always balance the size of cut itself against the sizes of the sets of created cut [1]. For this normalized cut method is being used. First it has to define the volume of set of nodes or vertices V which is denoted as Vol (V) is the number of edges with at least one end in the set of nodes or vertices V.

Let us partition the nodes of a graph into two disjoint sets say A and B. So the Cut (A, B) is the number of edges from the disjoint set A to connect a node in the disjoint set B. The formula for normalized cut values for disjoint sets A and B = Cut (A, B)/Vol (A) + Cut (A, B)/Vol (B).

2.6 Graph Partitions

Partition of graph means a division in clusters, such that similar kinds of vertices belong to a particular cluster [1]. In a real world vertices may share among different communities. When a graph is divided into overlapping communities then it is called a cover.

A graph with K-clusters and N-vertices, the possible number of Stirling number of the second kind is denoted as S(N, K). So the total number of possible partitions is said to be the Nth Bell number is given with the formula \( B_{N} = \sum\nolimits_{K = 0}^{N} {{\text{S}}(N,K)} \) [3]. When the value of N is large then B n becomes asymptotic [4].

While partitioning a graph having different levels of structure at different scales [5, 6], the partitions can be ordered hierarchically. So in this situation cluster plays an important role. Each cluster displays the community structure independently, which consists of set of smaller communities.

Partitioning of graph means dividing the vertices in a group of predefined size. So that the frequently used vertices are often combined together to form a cluster by using some techniques. Many algorithms perform a partition of graph by means of bisecting the graph. Iterative bisection method is employed to partition a graph into more than two clusters and this algorithm is called as Kernighan-Lin [7]. The Kernighan-Lin algorithm was extended to extract partitions of graph in any number of clusters [8].

Another popular bisection method is the spectral bisection method [9, 10], is completely based on the properties of spectrum of the Laplacian matrix. This algorithm is considered as quiet fast. According to Ford and Fulkerson [11] theorem that the minimum cut between any two vertices U and V of a graph G, is any minimum number of subset of edges whose deletion would separate U from V, and carries maximum flow from U to V across the graph G. The algorithms of Goldberg and Tarjan [12] and Flake et al. [13, 14] are used to compute maximum flows in graphs during cut operation. Some other popular methods for graph partition are level-structure partition, the geometric algorithm, and multilevel algorithms [15].

3 Proposed Algorithms and Analysis

3.1 Explanation

The proposed algorithm consists of five procedures. Procedure-I allows to read the details about number of communities and number of community members of all the communities. In this example the output has been derived after implemented using C++ programming language. The data related to community and their edges are read from two data files namely “commun1.txt” and “graph.dat”. Procedure-II which generates and assigns community member codes. Procedure-III creates the community adjacency matrix. Procedure-IV allows us to partition the community adjacency matrix by assigning ‘0’ over ‘1’ which indicates the edge between the community members of dissimilar communities. Finally Procedure-V displays every community’s adjacency matrix. From the adjacency matrices we can draw the community sub-graphs.

3.2 Example

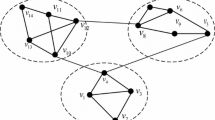
We propose a community graph [16, 17] with 22 individual communities from four different communities \( \left\{ {C_{1} ,C_{2} ,C_{3} ,C_{4} } \right\} \) which is shown in Fig. 3. We try to partition this graph into four sub-graphs of communities \( \left\{ {C_{1} ,C_{2} ,C_{3} ,C_{4} } \right\} \). We try to represent this graph in memory in an adjacency matrix form by following graph techniques which is shown in Fig. 4. Then we try to locate edges between communities members formed from two different communities.

Fig. 3
figure 3

Community graph of communities \( \left\{ {C_{11} \ldots C_{16} ,\,C_{21} \ldots C_{25} ,\,C_{31} , \ldots C_{34} , C_{41} \ldots C_{48} } \right\} \)

Full size image
Fig. 4
figure 4

Adjacency matrix of community graph in Fig. 3

Full size image

The black filled boxes indicate the edge between the community members of dissimilar communities which is indicated in Fig. 5. These edges are considered as edges between dissimilar communities. So these edges must be cut. Once such edges are cut, then the original graph can be partitioned into so many sub-graphs. And we can say that the graph has been partitioned across edges of community members of dissimilar communities. To do the edge cut operation, we assign 0 over 1 in the black filled boxes of adjacency matrix in Fig. 5. So that we can say there is no physical edge between those community members across the different communities. From the adjacency matrix of Fig. 5, we can construct four different adjacency matrices for the communities C 1, C 2, C 3, and C 4 which is shown in Fig. 6. For C 1 the community members are \( \left\{ {11,12,13,14,15,16} \right\} \). Similarly for C 2, C 3, and C 4 the community members are \( \left\{ {21,22,23,24,25} \right\}, \, \left\{ {31,32,33,34} \right\}, \) and \( \left\{ {41,42,43,44,45,46,47,48} \right\} \) respectively. From these four adjacency matrices, now we can construct the sub-graphs which are shown in Fig. 7.

Fig. 5
figure 5

Adjacency matrix of community graph after cut-off edges between community members of dissimilar communities

Full size image
Fig. 6
figure 6

Adjacency matrices of communities C 1 , C 2 , C 3, and C 4

Full size image
Fig. 7
figure 7

Communities \( \left\{ {C_{1} ,C_{2} ,C_{3} ,C_{4} } \right\} \)’s sub-graphs

Full size image

3.3 Output

4 Conclusions

We have partitioned our large community graph into sub-community graphs using the concepts of graph technique, especially by detecting an edge between the nodes of different communities. Initial portion of the work is a brief review of the literature on graph partition related to mathematical formulae as well as graph mining techniques. A simple graph technique for partition of a large community graph has been proposed. An appropriate example from social community network background has been represented using the graph theoretic concepts. The paper concludes with focusing on process of partitioning a community graph. There after the various sub-community graphs are to be shown in its adjacency matrix format. Hence extracting knowledge from a particular sub-community graph becomes easier and faster.