Keywords

1 Introduction

In the literature review of symmetric key cryptology, the stream ciphers are observe that to be one of the most important primitives. So far, stream cipher that has some kind of internal state which is regularly updated [1]. For instance there length is n bits, then the function [2] f can be defined as

$$ f:{{\mathbb{G}}{\mathbb{F}}}\,(2)^{n} \to {{\mathbb{G}}{\mathbb{F}}}\,(2) $$

The Trivium stream cipher was originally proposed by De Canniere and Preneel [1]. In data encryption primitives Trivium stream cipher is widely applicable both in hardware and in software level. This stream cipher is a hardware-oriented synchronous stream cipher, which claimed a key size of 80 bits and an initialization vector (IV) size of 80 bits and it remain consistent when it was submitted. In that approach, it presented in [3], Trivium stream cipher is algebraic in nature. Attacking on Trivium are propose by Babbage in [3], that evidence is given that internal state bits of Trivium can be protect with a time complexity \( c^{283.5} \). The study and analysis of Trivium literature proposed mainly the algebraic structure of the cipher which has the propensity basis on guess and determine types of attack or it may recover the internal state bits of the Trivium cipher which can be mounted and resist by algebraic attack [4]. We try to modify the literature structure of Trivium so that its appropriate structure can be used to provide a improve security. This modified version of Trivium relay the better security to the internal state recovery of that cipher attack.

1.1 Description of the Cipher

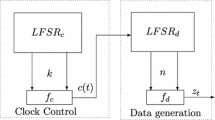
Trivium consists two processes that concentrate the values of 15 specific state bits and uses them both to update 3 bits of the internal state. Let \( s_{1} \), \( s_{2} \), …, \( s_{288} \) be the 288 internal bits and the key stream generated at a particular time i (i = 0, 1, …, n). This process is repeated for 4 * 288 = 1,152 times. So it can be summarized by the following generation of pseudo code [5] represent in Algorithm 1.

In each round of Trivium cipher a single bit include linear function of six state bits. Generally this key-stream process repeated until N \( \le \) \( 2^{64} \) bits of key-stream generated. Each state bits are rotated, and as well as the process is repeats in the same manner. The generation of key stream is described by the following pseudo-code [5] represent in Algorithm 2.

2 Study of Non-linear Feedback Shift Register

2.1 Structure of Non-linear Feedback Shift Register

A non-linear feedback shift register (NLFSR) works as same as a linear feedback shift register (LFSR) but there is some difference between them, in linear feedback shift register the feedback function is linear, that is it is only the combination of contents of L stages for a L length linear feedback shift register [4]. In non-linear feedback shift register feedback function is not linear, a non-linear feedback shift register is a combination of L stages of a L-length NLFSR [2, 6–8]. In non-linear contents are produced by adding a stage content to feedback (Fig. 1).

Fig. 1
figure 1

A NLFSR structure of length L

Full size image

The feedback function of NLFSR can be defined as

$$ s_{j} = f\left( {s_{L - 1} ,s_{L - 2} , \ldots ,s_{0} } \right)\;{\text{where}}\;{\text{j}} = \left( {L,L + 1,L + 2 \ldots } \right).$$

2.2 Non-linear Combination Generator

Non-linear combination generator is another type of a linear feedback shift register. More then one linear feedback shift register is used and each linear feedback shift register where output is a key bit. Output of these linear feedback shift register are combined for producing a final output bit [4, 7, 8]. Each output bit of each linear feedback shift register are combined non-linearly for producing a non-linear output bit.

A Non-linear feedback shift register state variables can be represented as \( x = (x_{0} ,x_{1} , \ldots x_{l - 1} ) \) which denote the state variable \( s = \left( {s_{0} ,s_{1} , \ldots s_{l - 1} } \right)\;\upvarepsilon\left( {0,1} \right)^{l}.\)

3 Implementation Details on Trivium Cipher

The linear correlations between key stream bits and internal state recovery bits are simple to compute due to the reason of \( {\mathbb{Z}}_{i} \) is simply describe to be equal to \( s_{66} \) \( \oplus \) \( s_{93} \) \( \oplus \) \( s_{162} \) \( \oplus \) \( s_{177} \) \( \oplus \) \( s_{243} \) \( \oplus \) \( s_{288} \). Trivium stream cipher state evolves in a non linear way i.e. not easy for an attacker to add these equations in order to efficiently recover the internal state [9]. 288-bit nonlinear feedback shift register are uses in Trivium. Trivium cipher uses nonlinear state-update three bits of the internal state and keystream bits are represented as a linear combination of the contents of six stages of its internal state.

This paper we try to describe the algebraic representation of Trivium. In that section we briefly explain some differential fault analysis of Trivium stream cipher and try to generate some the polynomial equation system that represent the inner state of Trivium cipher. Our attack description and the results are presented in next section respectively.

3.1 Proposed Work

In this paper we analyse the biases of Trivium cipher. As a case-study of Trivium cipher, we present a new method of finding linear feedback bits and the linear combination of keystream bits of the cipher. Our approach is to change some particular state bits without changing the elegant structure of stream cipher and compare the output with the original one. So far, our proposed method confined that some modification of statebits increases security level without changing internal structure of the cipher. We are able to show that statebit stream and generated new bit stream variables has a significant impact on the success of our algebraic attack on Trivium cipher.

3.2 Performance Analysis

The hardware testing eStream framework determined five conditions of performance based on power consumption, area compactness, throughput, simplicity and flexibility. Trivium cipher feedback can be allowing more than one bit to be per cycle processed. Our implemented testing key and IV performance result are described in Table 1 and testing stream encryption speed performance result described in Table 2.

Table 1 Testing key and IV setup speed
Full size table
Table 2 Testing stream encryption speed
Full size table

4 Analysis of Different Attacks on Trivium Cipher

Out of two variants of attacks state recovering attack is the first variant which tries to guess some state bits value. In that case it reduces the linear equations which can be implemented based on the elimination process. Another form of attack is known as distinguishing attack. This attack procedure collects information on keystream generation process and creates a distinguisher. Main focus stays only on state recovery attack [2]. As a polynomial expression F(K, IV) = Y, where K is the secret key of n bits (\( x_{1} \), \( x_{2} \) …., \( x_{n} \)) and IV is known publicly initialization vector (IV) of m bits (\( v_{1} \), \( v_{2} \) ….., \( v_{m} \)).

We use the expression \( F_{i} \)(K, IV) = \( Y_{i} \) is to represent the polynomial expression for the ith output bit of Trivium cipher [10]. Our main approach of this attack is to combine the equations in K but randomly representation of IV in such a manner which is low degree equations in the variable K [11]. The chosen IV s can be chosen in such a way that linear equations of unknowing bits in K can be obtained. In fact internal statebits of Trivium consists of 288 bits which are set in 3 shift registers respectively [11]. In generally some primitive polynomials can be determined to use to create an LFSR. This LFSR has the degree of the polynomial that will cycle over all non-zero states in Trivium [10, 12, 13]. The pseudo number generation in n bit shift registers are randomly scrolls between (2n − 1) values. This process quickly computes using less number of combinational logic. So basically when it reaches its final state, it tries to traverse the sequence exactly as before [9]. This External LFSR is one way of implementing i.e. all XOR gates are sequentially into one another and ends up as the input to the least or most significant bit of the LFSR [11]. So XORs are external form of the shift register and in internal structure of LFSR XOR gates are not sequential [11]. Recall that if f(X) \( \varepsilon \) \( {\mathbb{F}}_{p} [X] \) is a polynomial of n degree such that f(0) \( \ne \) 0, then there is positive integer \( \phi \) \( \le \) \( q^{n} \)−1 such that f(X) divides \( X^{\phi } \) − 1. The least such \( \phi \) is called the order of f(X) and is denoted by f(X). If f(X) is any nonzero polynomial in \( {\mathbb{F}}_{p} [X] \), then we can write f(X) = \( X^{\varsigma } \) g(X), where \( \varsigma \) \( \ge \) 0 and g(X) \( \varepsilon \) \( {\mathbb{F}}_{p} [X] \).

In Raddum’s approach the key stream generation procedure of Trivium takes one linear combination of 6 sequence bits and 2 sequence bits from A, B and C registers. The key stream bits are represented in following way [14, 15].

$$ \begin{gathered} z_{66} = A_{93} \oplus A_{66} \oplus B_{81} \oplus B_{66} \oplus C_{111} \oplus C_{66} \hfill \\ z_{69} = A_{96} \oplus A_{69} \oplus B_{84} \oplus B_{69} \oplus C_{113} \oplus C_{68} \hfill \\ \end{gathered} $$

4.1 Reasonable Degree Changes in Trivium Cipher

In our paper, Trivium reasonable modification is easy and elegant structure. The proposed modification is minimizing the number of linear equations that appears during the previous clock bits [12, 13]. In Trivium, our proposed modified equations forms a higher degree than the original structure. In our paper we try to compare with original algebraic structure of Trivium and modified structure of Trivium. In linear equations and other lower degree polynomial equations can be guessed and finally the remaining secret bits can be recovered. The proposed idea of modification tries to discard this simple recovery of bits even some bits which are guessing bit position [10–12]. So this approach may be determined if feedback of the product term comes in the output bits in prior manner. This modify key generation process is described by the following Algorithm 3.

In that section we try to get linear equations comparison with of the original structure and of Trivium cipher [9]. As we mentioned previously, the feedback product of the cipher comes first in output prior to the original structure [11, 13]. Consequently \( s_{1} \), \( s_{94} \) and \( s_{178} \) are replaced by \( t_{3} \), \( t_{1} \), and \( t_{2} \) respectively. After 65 clocks with update of \( s_{1} \), \( s_{94} \) or \( s_{178} \) in such a manner. The Trivium cipher modification approach does not induced any extra logic gate except a reasonable change in the position of the feedback function. This procedure is to reduce the number of linear equations of the cipher. The difference between the degrees of algebraic structure of cipher with the original version of the cipher is described in Fig. 2.

Fig. 2
figure 2

Comparison of degree of trivium equation with algebraic attack

Full size image

After the reasonable changes we get first 33 linear equations which is same as original cipher. As we compare with 66 linear equations of the original cipher, some degrees are reasonably changed step by step. Finally we compare our version with the original one, we get some reasonable high degrees rather than the original version is described in Fig. 3. The sequential guessing bits are not ideal only the reason of product terms of sequential bits [13, 16]. Trivium structure has three registers which is updating the feedback variables of the three registers and it becomes mutually dependent based on the degrees of equations.

Fig. 3
figure 3

Comparison between modified structure of trivium with algebraic attack

Full size image

5 Conclusion and Future Work

In this paper we try to present some weakness of Trivium stream cipher which provide random sequence generators through non-linear shift registers. Several research problems on Trivium is till remain unanswered like patterns of behavior, algebraic attack, lengths, weak keys etc. So questions arises basis on its bits security level which can be rapidly increase with equal number of statebits. Under this design paradigm, we present reduced variant sized modifications of that stream generator, which increases the bit security level of Trivium cipher. We speculate the properties identified in the reduced sized model would remain invariant in the original ones and it would be worthwhile to innovate a new framework of Trivium cipher.