Keywords

1 Introduction

The rapid development of computing science, technology, and mathematical logic put forward many new requirements, thus contributing to the non-classical logic and the rapid development of modern logic [1]. The non-commutative logical algebras are the algebraic counterpart of the non-classical logic. Non-commutative residuated lattice are algebraic counterparts of non-commutative monoidal logic [2]. Pseudo-BL-algebras and pseudo-MTL-algebras are non-commutative residuated lattices [3].

The theory of filters functions well not only in non-classical logic, but also in Computer Science. From logical point of view, various filters correspond to various sets of provable formulae [4]. Hájek introduced the notions of filters and prime filters in BL-algebras and proved the completeness of Basic Logic BL [5]. In [6], Turunen proposed the notions of implicative filters and Boolean filters of BL-algebras and proved the equivalence of them in BL-algebras. In [7–13], filters of pseudo-MV algebras, commutative residuated lattice, triangle algebras, pseudo-effect algebras, and pseudo-hoops were studied.

Fuzzy sets were introduced in 1965 by Zadeh [14]. At present, fuzzy filters ideas have been a useful tool to obtain results on classical filters and been applied to other algebraic structures. In recent years, fuzzy logic-based reasoning seems to be active and in-depth study of these domestic and international research works carried out to explore some new, mainly related to the formalization of fuzzy logic and related algebraic structure.

We find that the structures of the non-commutative logical algebras can be described by the tools of fuzzy filters. Therefore, in this paper, the theory of fuzzy weak Boolean filters in non-commutative residuated lattices is studied, which lays a good foundation for the further research in non-commutative logical algebras.

2 Review of Preliminaries

First, we recall some basic definitions and results which will be needed later (see details in [2, 3, 10, 13, 15–17]).

Definition 1

A lattice-ordered residuated monoid is an algebra (K,∨ , ∧ , ⋆ , → , ↪ , e) satisfying the following conditions:

  1. (1)

    (K, ∨, ∧) is a lattice,

  2. (2)

    (K,⋆, e) is a monoid,

  3. (3)

    x ⋆ y ≤ z iff x ≤ y → z iff y ≤ x ↪ z for all x, y, z ∊ K.

A lattice-ordered residuated monoid K is called integral if x ≤ e for all x ∊ K. In an integral lattice-ordered residuated monoid, we use “1” instead of e.

Definition 2

A residuated lattice is a bounded and integral residuated lattice-ordered monoid, i.e., a residuated lattice is an algebra (K, ∨ , ∧ , ⋆ , → , ↪ , 0, 1) satisfying the following conditions:

  1. (1)

    (K, ∨ , ∧ , ⋆ , → , ↪ , 0, 1) is a bounded lattice,

  2. (2)

    (K, ⋆ , 1) is a monoid,

  3. (3)

    x ⋆ y ≤ z iff x ≤ y → z iff y ≤ x ↪ z for all x, y, z ∊ K.

Lemma 1

(Jipsen, Tsinakis and Blount, Zhang [3, 15, 16]) In a non-commutative residuated lattice K, the following properties hold for all x, y, z ∊ K

  1. (1)
  2. (2)
    $$ x \le (x \rightarrow y) \hookrightarrow y,x \le (x \hookrightarrow y) \rightarrow y, $$
  3. (3)
    $$ x \le y\,{\text{iff}}\;x \to y = 1\; {\text{iff}}\;x \hookrightarrow y = 1, $$
  4. (4)
  5. (5)
    $$ x \le y \rightarrow y \rightarrow z \le x \rightarrow z\;{\text{and}}\;y \hookrightarrow z \le x \hookrightarrow z, $$
  6. (6)
    $$ x \le y \rightarrow z \rightarrow x \le z \rightarrow y\;{\text{and}}\;z \hookrightarrow x \le z \hookrightarrow y $$
  7. (7)
    $$ x \rightarrow y \le (z \rightarrow x) \rightarrow (z \rightarrow y),\;x \hookrightarrow y \le (z \hookrightarrow x) \hookrightarrow (z \hookrightarrow y), $$
  8. (8)
    $$ x \rightarrow y \le (y \rightarrow z) \hookrightarrow (x \rightarrow z),\;x \hookrightarrow y \le (y \hookrightarrow z) \rightarrow (x \hookrightarrow z), $$
  9. (9)
    $$ x \vee y \le ((x \rightarrow y) \hookrightarrow y) \wedge ((y \rightarrow x) \hookrightarrow x) $$
  10. (10)
    $$ x \vee y \le ((x \hookrightarrow y) \rightarrow y) \wedge ((y \hookrightarrow x) \rightarrow x). $$

In the sequel, we shall use K to denote a non-commutative residuated lattice and define \( x^{-} = x \to 0,\,x^{\sim} = x \hookrightarrow 0 \) for any x ∊ K.

Definition 3

A filter of K is a non-empty subset N of K such that for all x, y ∊ K, one of the following holds

  1. (1)

    if x, y ∊ N, then x ⋆ y ∊ N and

    if x ∊ N and x ≤ y, then y ∊ N,

  2. (2)

    1 ∊ N and x, x → y ∊ N imply y ∊ N,

  3. (3)

    1 ∊ N and \( x,x\, \hookrightarrow\, y \in N \) imply y ∊ N.

Definition 4

For any x, y ∊ K, a filter N of K is called Boolean if \( x \vee x^{ - } \in N \) and \( x \vee x^{ \sim } \in N \).

Definition 5

Let N be a subset of K. Then N is called a weak Boolean filter of K if for all x, y, z ∊ K, the following conditions hold

  1. (1)

    1 ∊ N,

  2. (2)

    (x → y) ⋆ z ↪ ((y ↪ x) → x) and z ∊ N implies \( (x\,\rightarrow\,y) \hookrightarrow y \in N \),

  3. (3)

    z ⋆ (x ↪ y) → ((y → x) ↪ x) and z ∊ N implies (x ↪ y) → y ∊ N.

3 Fuzzy Weak Boolean Filters of Non-commutative Residuated Lattice

In this section, we introduce and investigate the properties of fuzzy weak Boolean filters of non-commutative residuated lattice and further characterize the fuzzy weak Boolean filters as an extension work of [11].

Definition 6

Let T be a fuzzy set of K. T is called a fuzzy filter of K if for all t ∊ [0, 1], T t is either empty or a filter of K.

Definition 7

Let T be a fuzzy filter of K. Then T is a fuzzy Boolean filter of K, if for all x ∊ K, \( T(x \vee x^{ - } ) = T(1) \) and \( T(x \vee x^{ \sim } ) = T(1) \).

Definition 8

Let T be a fuzzy subset of K. Then T is called a fuzzy weak Boolean filter of K if for all x, y, z ∊ K, the following conditions hold

  1. (1)
    $$ T(1) \ge T(x), $$
  2. (2)
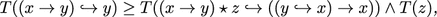
  3. (3)

Inspired by [11], we can get the following results.

Theorem 1

Let T be a fuzzy filter of K. T is a fuzzy weak Boolean filter of K if and only if for each t ∊ [0, 1], T t is either empty or a weak Boolean filter of K.

Theorem 2

Let T be a fuzzy filter of K. T is a fuzzy weak Boolean filter of K if and only if \( T_{T(1)} \) is a weak Boolean filters of K.

Corollary 1

Let N be a non-empty subset of K. N is a weak Boolean filter of K if and only if χ N is a fuzzy weak Boolean filter of K.

Next, we characterize the fuzzy weak Boolean filters.

Theorem 3

Let T be a fuzzy filter of K. Then the followings are equivalent:

  1. (1)

    T is a fuzzy weak Boolean filter,

  2. (2)

    \( T((x \rightarrow y) \hookrightarrow y) = T((x\, \rightarrow\, y) \hookrightarrow ((y \hookrightarrow x) \rightarrow x))) \) for any x, y ∊ K,

  3. (3)

    \( T((x\,\hookrightarrow\, y) \rightarrow y) = T((x \,\hookrightarrow\, y) \rightarrow ((y\, \rightarrow\, x) \hookrightarrow x))) \) for any x, y ∊ K.

Proof

(1) ⇒ (2). Let T((x → y) ↪ ((y ↪ x) → x))) = t, then ((x → y) ↪ ((y ↪ x) → x)) ∊ T t . 1 ∊ T t , (((x → y) ⋆ 1) ↪ ((y ↪ x) → x) ∊ T t , hence (x → y) ↪ y ∊ T t , i.e., T((x → y) ↪ y) ≥ t = T(((x → y) ↪ ((y ↪ x) → x)). The inverse inequation is obvious since T is isotone and (x → y) ↪ y ≤ (x → y) ↪ ((y ↪ x) → x).

  • (1) ⇒ (3). Similar to (1) ⇒ (2).

  • (2) ⇒ (1). Let T(((x → y) ⋆ z) ↪ ((y ↪ x) → x) ∧ T(z) = t, then ((x → y) ⋆ z) ↪ ((y ↪ x) → x, z ∊ T t . Since T t is a filter, (x → y) ↪ ((y ↪ x) → x ∊ T t , and (x → y) ↪ y ∊ T t , i.e., T((x → y) ↪ y) ≥ T(((x → y) ⋆ z) ↪ ((y ↪ x) → x) ∧ T(z).

  • (3) ⇒ (1). Similar to (2) ⇒ (1).

Theorem 4

Every fuzzy weak Boolean filter of K is a fuzzy filter.

Proof

Let T(x ↪ y) ∧ T(x) = t, then x ↪ y, x ∊ T t . Since we have ((y → y) ⋆ x) ↪ ((y ↪ y) → y) = x ↪ y ∊ T t , we have y = (y → y) ↪ y) ∊ T t . Hence, T(y) ≥ T(x ↪ y) ∧ T(x) and T is a fuzzy filter.

Theorem 5

Let T be a fuzzy filter of K. Then the followings are equivalent

  1. (1)

    T is a fuzzy weak Boolean filter,

  2. (2)

    T(y) ≥ T((y → z) ↪ (x → y)) ∧ T(x) for any x, y, z ∊ K,

  3. (3)

    T(y) ≥ T((y ↪ z) → (x ↪ y)) ∧ T(x) for any x, y, z ∊ K.

Proof

(1) ⇒ (2). Let \( T((y \rightarrow z) \hookrightarrow (x \rightarrow y)) \wedge T(x) = t \), then \( (y \rightarrow z) \hookrightarrow (x \rightarrow y) = x \rightarrow ((y \rightarrow z) \hookrightarrow y),x \in T_{t} \). We get \( (x \rightarrow y) \hookrightarrow y \in T_{t} \). And \( z \le y \to z \), \( (x \rightarrow z) \hookrightarrow y \le z \hookrightarrow y \in T_{t} \). hence \( z \hookrightarrow y \in T_{t} \). And we have \( (y \rightarrow z) \hookrightarrow y \le (y \rightarrow z) \hookrightarrow ((z \hookrightarrow y) \rightarrow y) \in T_{t} \). Then we get \( (y \rightarrow z) \hookrightarrow z \in T_{t} \) since T is a fuzzy weak Boolean filter of K. And \( (y \rightarrow z) \hookrightarrow z \le (z \hookrightarrow y) \rightarrow ((y \rightarrow z) \hookrightarrow y) \); then \( (z \hookrightarrow y) \rightarrow ((y \rightarrow z) \hookrightarrow y) \in T_{t} \). So \( (z \hookrightarrow y) \rightarrow y \in T_{t} \), since \( z \hookrightarrow y \in T_{t} \), \( y \in T_{t} \), i.e., \( T(y) \ge T((y \rightarrow z) \hookrightarrow (x \rightarrow y)) \wedge T(x) \).

  • (1) ⇒ (3). Similar to (1) ⇒ (2).

  • (2) ⇒ (1). Let \( T((x \rightarrow y) \hookrightarrow ((y \hookrightarrow x) \rightarrow x)) = t \) for all x, y ∊ K, then \( (x \rightarrow y) \hookrightarrow ((y \hookrightarrow x) \rightarrow x) \in T_{t} \). Since \( (((x \hookrightarrow y) \hookrightarrow y) \rightarrow 1) \hookrightarrow (((x \rightarrow y) \hookrightarrow ((y \hookrightarrow x) \rightarrow x))) \rightarrow ((x \rightarrow y) \hookrightarrow y)) = ((x \rightarrow y) \hookrightarrow ((y \hookrightarrow x) \rightarrow x)) \rightarrow (((x \rightarrow y) \hookrightarrow y) \hookrightarrow ((x \rightarrow y) \hookrightarrow y)) = (x \rightarrow y) \hookrightarrow ((y \hookrightarrow x) \rightarrow x) \in T_{t} \), \( (x \hookrightarrow y) \hookrightarrow y \in T_{t} \).

  • (3) ⇒ (1). Similar to (2) ⇒ (1).

Remark 1

Let T be a fuzzy filter of K. Then the followings are equivalent:

  1. (1)

    T is a fuzzy weak Boolean filter,

  2. (2)

    \( T((y \hookrightarrow x) \rightarrow x) \ge T((x \rightarrow y) \hookrightarrow ((y \rightarrow x) \hookrightarrow x)) \) for any x, y ∊ K,

  3. (3)

    \( T((y \rightarrow x) \hookrightarrow x) \ge T((x \hookrightarrow y) \rightarrow ((y \hookrightarrow x) \rightarrow x)) \) for any x, y ∊ K.

Theorem 6

Let T be a fuzzy filter of K. Then the followings are equivalent

  1. (1)

    T is a fuzzy weak Boolean filter,

  2. (2)

    \( T((x \rightarrow y) \hookrightarrow x) = T(x) \) for any x, y ∊ K,

  3. (3)

    \( T((x \hookrightarrow y) \rightarrow x) = T(x) \) for any x, y ∊ K.

Proof

(1) ⇒ (2). Let T be a fuzzy weak Boolean filters of K and \( T((x \rightarrow y) \hookrightarrow x) = t \). Then \( (x \rightarrow y) \hookrightarrow x \in T_{t} \). And \( 1 \in T_{t} \), \( (x \rightarrow y) \hookrightarrow (1 \rightarrow x) = (x \rightarrow y) \hookrightarrow x \in T_{t} \), we get \( x \in T_{t} \), i.e., \( T(x) \ge t = T((x \rightarrow y) \hookrightarrow x) \). The inverse inequation is obvious since T is isotone and \( x \le (x \rightarrow y) \hookrightarrow x \).

  • (1) ⇒ (3). Similar to (1) ⇒ (2).

  • (2) ⇒ (1). Let \( T((y \rightarrow z) \hookrightarrow (x \rightarrow y)) \wedge T(x) = t \) for all x, y, z ∊ K, then \( (y \rightarrow z) \hookrightarrow (x \to y),x \in T_{t} \). Since \( (y \rightarrow z) \hookrightarrow (x \rightarrow y) = x \rightarrow ((y \rightarrow z) \hookrightarrow y),x \in T_{t} \) and T t is a filter, \( (y \rightarrow z) \hookrightarrow y \in T_{t} \), and \( T((y \rightarrow z) \hookrightarrow y) = T(y) \ge t = T((y \rightarrow z) \hookrightarrow (x \to y)) \wedge T(x) \), and we have T is a fuzzy weak Boolean filter.

  • (3) ⇒ (1). Similar to (2) ⇒ (1).

Remark 2

Let T be a fuzzy filter of K. Then the followings are equivalent

  1. (1)

    T is a fuzzy weak Boolean filter,

  2. (2)

    \( T(x^{-} \hookrightarrow x) = T(x) \) for any x, y ∊ K,

  3. (3)

    \( T(x^{{^{ \sim } }} \to x) = T(x) \) for any x, y ∊ K.

Theorem 7

Let T, g be two fuzzy filters of K which satisfy \( T \le g,T(1) = g(1) \). If T is a fuzzy weak Boolean filters of K, so is g.

Proof

Let \( T((x \rightarrow y) \hookrightarrow x) = t \) for all x, y ∊ K, then we let \( z = (x \rightarrow y) \hookrightarrow x,z \rightarrow z = 1 \in T_{t} \). Since \( z \rightarrow ((x \rightarrow y) \hookrightarrow x) = (x \rightarrow y) \hookrightarrow (z \rightarrow x) = 1 \in T_{t} \), we have \( (x \rightarrow y) \hookrightarrow (z \rightarrow x) \le ((z \rightarrow x) \rightarrow y) \hookrightarrow (z \rightarrow x) \in T_{t} \).

Since T t is a weak Boolean filter of K, we get \( g(1) = T(1) \le T(z \to x) \le g(z \to x) \). Thus \( z \to x \in g_{t} \) and \( x \in g_{t} \) since \( z \in g_{t} \). Then we have g as a fuzzy weak Boolean filter.

Remark 3

Every fuzzy filter T of a residuated lattices K is a fuzzy weak Boolean filter if and only if χ K is a fuzzy weak Boolean filter.

Theorem 8

Every fuzzy weak Boolean filter T of K is equivalent to a fuzzy Boolean filter.

Proof

Let T be a fuzzy weak Boolean filter of K. Since \( T((x \vee x^{-})^{-} \hookrightarrow (x \vee x^{-})) = T((x^{-} \wedge x^{- -}) \hookrightarrow (x \vee x^{-})) = T(1) \), we have \( T(x \vee x^{ - } ) = T(1) \). Similarly, we can get \( T(x \vee x^{ \sim } ) = T(1) \), so we have T as a fuzzy Boolean filter.

Conversely, suppose T is a fuzzy Boolean filter of K and let \( T(x^{-} \hookrightarrow x) = t \). Then \( x^{-} \hookrightarrow x \in T_{t} \) and T t is a Boolean filter since \( (x \vee x^{-} \hookrightarrow x = (x \hookrightarrow x) \wedge (x^{-} \hookrightarrow x) = x^{-} \hookrightarrow x \in T_{t} \). And T t is a Boolean filter, so \( x \vee x^{ - } \in T_{t} \); then we have \( x \in T_{t} \) and \( T(x) \ge T(x^{-} \hookrightarrow x) = t \). The inverse inequation is obvious, so we get \( T(x) = T(x^{-} \hookrightarrow x) \). Dually, we can get \( T(x) = T(x^{ \sim } \to x) \). Thus T is a fuzzy weak Boolean filters.