Floating Point-based Universal Fused Add–Subtract Unit

Abstract

This paper describes fused floating point add–subtract operations and which is applied to the implementation of fast fourier transform (FFT) processors. The fused operations of an add–subtract unit which can be used both radix-2 and radix-4 butterflies are implemented efficiently with the two fused floating point operations. When placed and routed using a high-performance standard cell technology, the fused FFT butterflies are about may be work fast and gives user-defined facility to modify the butterfly’s structure. Also the numerical results of the fused implementations are more accurate, as they use rounding modes is defined as per user requirement.

1 Introduction

Traditionally, most DSP applications have used fixed-point arithmetic to reduce delay, chip area, and power consumption. Fixed-point arithmetic has serious problems of overflow, underflow, scaling, etc. Single-precision floating point arithmetic is a potential solution because of no overflow or underflow, automatic scaling [3].

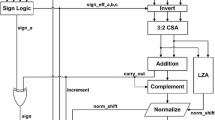
Two new fused floating point element implementation: (1) fused dot product contains multiplies two pair of floating point data, add (or subtract) the product (2) fused add–subtract contains add a pair of floating point data, and simultaneously subtract the same data [1].

It is traditional floating point adder which consist only addition of only valid floating point numbers. They work inefficiently when given data are not a floating point number and also it has some limitation that they can perform only programmer-defined rounding method due this reason if other rounding method we have use then again we have to edit program and change the data for new rounding method, so it can be neglected in proposed floating point adder.

All research is related to Xilinx SPARTAN 6 kit [5, 7] by using compilation software Xilinx version: 13.2. Xilinx is FPGA stimulator to estimate output of from Verilog code in terms of input–output buffers, maximum delay (longest path execution of circuit), area in terms of lookup table (LUTs).This software is used for VHDL and Verilog code implementation, stimulation and generating program for dump on FPGA kit.

2 Basic of Floating Point

The Institute of Electrical and Electronics Engineers (IEEE) Standard for Floating Point Arithmetic (IEEE 754) [4] is a technical standard established by the IEEE. This standard specifies the basic types of representation.

• Half Precision (16-bits or 2-bytes)

• Single Precision (32-bits or 4-bytes)

• Double Precision (64-bits or 8-bytes).

The format of a floating point number comprises 3 types of bits presented in the following Fig. 1.

Fig. 1

Single-precision floating point format

• Recall that exponent field is 8 bits for single precision

• E can be in the range from 0 to 255

• E $=$ 0 and E $=$ 255 are reserved for special use (discussed later)

• E = 1 to 254 are used for normalized floating point numbers

• Bias = 127 (half of 254), val(E) = E $-$127

• val(E=1) = $-126$, val(E=127) = 0, val(E=254) = 127.

• IEEE 754 standard specifies four modes of rounding

• 1. Round to nearest even: default rounding mode increment result if: rs = “11” or (rs = “10” and fln = ‘1’). Otherwise, truncate result significant to 1. f1f2...fln

• 2. Round toward $+\infty$: result is rounded up Increment result if sign is positive and r or s = ‘1’

• 3. Round toward $-\infty$: result is rounded down Increment result if sign is negative and r or s = ‘1’

• 4. Round toward 0: always truncate result.

3 Normal Addition–Subtraction Rule

$$\begin{aligned} \begin{array}{ll} {{{ + 1}}{{.1234}}} &{} {{{ - 1}}{{.1234}}} \\ {{{ + 1}}{{.2456}}} &{} {{{ - 1}}{{.2456}}} \\ {\overline{{{{ + 2}}{{.4690}}}} } &{} {\overline{{{{ - 2}}{{.4690}}}} } \\ \end{array} \end{aligned}$$

If we take normal addition or subtraction, consider a two numbers [Greater (G) and Lesser (L)] magnitude wise then only 4 combination are possible which are given in Table 1 [2].

Table 1 Signed addition or subtraction rules

After watching all examples, we came to conclusion that in addition and substation when there same sign number added or substrate then only add or subtract, respectively. Similarly, when two numbers have different signs, then we can use opposite function, i.e., subtract or add.

4 Study of FP Arithmetic Algorithms

Floating Point addition steps

Assume 32  bit binary number and then by applying algorithm for normal addition by calculator and by using FP addition algorithm stepwise.

• A = ${32^{\prime }}$b0__0111_1000__1011_1010_0000_1111_0110_110;

• B = ${32^{\prime }}$b0__0111_0011__0101_0000_0000_0011_1111_111;

• A = 1.3490607*E$-$2, B = 3.2044944*E$-$4.

4.1 Calculation From Calculator

1st step align decimal point

2nd step add

• 1.3490607 * E$-$2

• +0.032044944*E$-$2

• +1.381105644*E$-$2

3rd Normalize result

4.2 Detailed Bitwise Example

$$\begin{aligned} \begin{array}{lll} S &{} EXP &{} Mantissa (M)\\ 0 &{} 01111000 &{} 1011\_1010\_0000\_1111\_0110\_110\\ 0 &{} 01110011 &{} 0101\_0000\_0000\_0011\_1111\_111\\ \end{array} \end{aligned}$$

(1)

Find Greater no. and lesser no. and assign it [6].

• G = 0 01111000 1011_1010_0000_1111_0110_110

• L = 0 01110011 0101_0000_0000_0011_1111_111

• 1st step

  • Align radix point by using True exponent value difference

  • G_exp_t $= 0111\_1000(120)-0111\_1111= 1111\_1001(-7)$

  • L_exp_t $= 0111\_0011(115)-0111\_1111= 1111\_0100(-12)$

  • Ed = G_exp-L_exp = 5

  • Shift Lesser no. to right by Ed value

  • Shift_L_m = 1.0101_0000_0000_0011_1111_111(0)

  • Shift_L_m = 0.10101_0000_0000_0011_1111_111(1)

  • Shift_L_m = 0.010101_0000_0000_0011_1111_111(2)

  • Shift_L_m = 0.0010101_0000_0000_0011_1111_111(3)

  • Shift_L_m = 0.00010101_0000_0000_0011_1111111(4)

  • Shift_L_m = 0.0000_1010_1000_0000_0001_111_111(5)

• 2nd step addition of mantissa depend on signs of both no. (Table 1) and store last bits for rounding

  • 1.1011_1010_0000_1111_0110_110

  • +0.0000_1010_1000_0000_0001_111_111

  • 01.1100_0100_1000_1111_1000_101_111

  • Result_m = 01.1100_0100_1000_1111_1000_101_111

• 3rd step normalize mantissa result

  • n_Result_m = 01.1100_0100_1000_1111_1000_101_111

  • (For if result is m = 00.0010_0100_1000_1111_1000_101_111

  • Normalize now m = 01.0010_0100_0111_1100_0101_111_000)

  • (For if result is m = 10.0010_0100_1000_1111_1000_101_111

  • Normalize now m = 01.00010_0100_1000_1111_1000_101_111)

• 4th step Rounding (Round toward 0: always truncate result)

  • Round_Result_m = 01.1100_0100_1000_1111_1000_101

• 5th Step After rounding normalize

  • n_Result_m = 01.1100_0100_1000_1111_1000_101

  • Final Result sig_G, G_exp, n_Result_m

  • Sum = 0 0111_1000 1100_0100_1000_1111_1000_101

    • +1.3811056 * $\mathrm{{E}}-2$

    • +1.381105644 * $\mathrm{{E}}-2$ (From actual calculation)

5 Floating Point Adders

This contains original floating point adder and proposed floating point adder. Due three limitations like it will also work on invalid floating point, rounding mode, inefficient swap in greater and lesser number when both number have same sign and same exponent. To remove all limitations, we can see their proposed model satisfied in all three manners.

5.1 Traditional Floating Point Adder

Basic Floating Point Addition Algorithm [1, 3, 8]: The straightforward basic floating point addition algorithm requires the most serial operations. It has the following steps: (Fig. 2)

Fig. 2

Traditional floating point adder

• 1. Exponent subtraction: Perform subtraction of the exponents to form the absolute difference $\left| {{{E}}_{{{a}}} - {{E}}_{{{b}}} } \right| = {{d}}$.

• 2. Alignment: Right shift the significant of the smaller operand by d bits. The larger exponent is denoted Ef .

• 3. Significant addition: Perform addition or subtraction according to the effective operation. The result is a function of the op-code and the signs of the operands.

• 4. Conversion: Convert a negative significant result to a sign-magnitude representation. The conversion requires a two’s complement operation, including an addition step.

• 5. Leading one detection: Determine the amount of left shift needed in the case of Subtraction yielding cancellation. For addition, determine whether or not a 1-bit right shift is required. Then priority-encode the result to drive the normalizing shifter.

• 6. Normalization: Normalize the significant and update Exponent appropriately.

• 7. Rounding: Round the final result by conditionally adding as required by the IEEE standard. If rounding causes an overflow, perform a 1-bit right shift and increment Ef.

Fig. 3

Proposed floating point adder

5.2 Proposed Floating Point Adder

Proposed Floating Point Addition Algorithm: The straightforward derived floating point addition algorithm requires the most serial operations. It has the following steps: (Fig. 3)

• 1. Check given number is floating point number or invalid floating point enable other operation or enable not a FP no to show given data is invalid.

• 2. If given number is valid floating point number then sort out greater and lesser number from data comparing its magnitude.

• 3. Exponent subtraction: Perform subtraction of greater exponents to lesser exponent ${{E}}_{{G}}-{{E}}_{{L}} ={{d}}$.

• 4. Alignment: Right shift the significant of the lesser mantissa by d bits and store last 3 shifted bits.

• 5. Significant addition: Perform addition according to their signs take decision.

• 6. Normalize result: check result is overflow or not and then according to condition adjust exponent.

• 7. Rounding: Check the rounding mode and perform rounding on the result with the help of last 3 stored bits.

• 8. Normalize result: Check result is overflow or not and then according to condition adjust exponent and Display the result.

To remove all limitation in this, we have use 1st check valid floating point or not then for selective rounding, we have given choice to user mode, i.e., user-defined rounding modes to select round mode by giving signals to round_mode pins, and finally, we have to check exact greater or lesser number by comparing all 31 bits. Similarly, we can create substrater module referring Table 1 and then, we serially and parallel combination of adder and substrater finally we made fuse model of one adder and one substrater and we have advantage that fused required less numbers of LUT’s and less delay to get final output as if we use both different models of adder and subtract.

6 Proposed Floating Point Work Result

This shows all main modules implementations in RTL and outputs waveforms with respect to Xilinx SPARTAN 6 kit [7] stimulation on Xilinx software.

Fig. 4

Adder

Fig. 5

Subtracter

6.1 Proposed Models RTL View

Figures 4, 5 and 6.

Fig. 6

Add–subtracter

Fig. 7

Adder output waveform

Fig. 8

Subtracter output waveform

Fig. 9

Add–subtracter output waveform

Table 2 All modules details of implementations

6.2 Proposed Models Output Waveform

Figures 7, 8 and 9.

7 Comparisons of all Modules

See Table 2.

Table 3 All modules comparisons in terms of percentage w.r.t. adder

Table 4 Basic comparison of programming styles in Verilog on demo floating point adder

Fig. 10

LUT

Fig. 11

IOB

Fig. 12

Delay

Fig. 13

Comparison in percentage

8 Conclusions

In proposed floating point adder have two different functions from traditional floating point adder to provide user-defined adder. First is to check the given data are valid floating point number or not. Second is to give privilege to select rounding modes (i.e., user-defined rounding mode selection and default is truncating). While programming, we used different methods like by using TASK, function, and normal programming. After comparing all types of models of floating point adder, we came to conclusion that we modified traditional adder and able to prove that when we use functions in programming has good result at cost of saving 2 % number of LUTs and 7.8 % reduce delay (referring Table 4 Basic comparison of programming styles in Verilog on demo floating point adder). So we finally decided that we are using functions in all Verilog design programs to give best output.

After watching results from Tables 2, 3 and Figs. 10, 11, 12, 13, we came to know that we are saving in proposed floating point add–subtract model is 68 % decrease in IOBs, saving 23 % number of LUTs and 88 % reduce delay as compared to the single adder, single subtracter, serial adder and subtracter, Parallel adder and subtracter.