Distributed Online Patrolling with Multi-agent Teams of Sentinels and Searchers

Abstract

We consider the problem of patrolling an assigned area using a team of heterogeneous robots consisting of sentinels and searchers in the presence of stochastic arrivals of attacks. Sentinels and searchers operate using a different sensor model featuring a tradeoff between accuracy and the sensed area. Using an approach based on queuing theory, we derive an accurate analytic characterization of the patrolling performance that can be used to predict the behavior of a given configuration or inform the composition of a team in order to meet a desired target performance. Extensive simulation results corroborate our theoretical findings.

1 Introduction

Among the many uses envisioned for teams of coordinated autonomous robots, tasks related to intelligence, surveillance and reconnaissance (ISR) continue to be at the forefront of research in distributed robotics. Teams of robots can implement search and patrolling strategies that complement and enhance human performance while reducing costs, increasing resilience, and decreasing operational risks for humans. Recent developments in the area of unmanned aerial vehicles (UAVs) have added momentum to this very active research area, in particular with the development of vertical take-off and landing vehicles, such as quadrotor UAVs [10].

In the recent past we have studied the problem of robotic search and patrolling using a single quadrotor UAV [1, 5]. Our initial modeling efforts and theoretical findings were corroborated with extensive field experiments demonstrating the validity of our assumptions [4]. A characteristic aspect of this class of vehicles is that their sensing resolution can be adjusted on the fly byKeeping this in mind varying their elevation—a fact already evidenced in [14]. Therefore, when planning how to allocate the search effort in space and time, one should also explicitly consider the variable sensor accuracy, defined here as detection probabilities. In fact, sensors and sensor processing algorithms have preferred operating conditions and one should strive to operate in those regions, when possible. Needless to say, operating in a regime offering the highest accuracy often comes at the cost of reducing the sensing area, thus creating opposing objectives. Our former works in this area have exactly explored this tradeoff in the single agent case.

In this paper we extend our existing work by considering how teams of heterogeneous robots can jointly patrol an assigned area. Our setup consists of two classes of robots, called sentinels and searchers. Sentinels and searchers operate at different elevations, and their sensors are then subject to different performances. The role of sentinels is to detect intrusions¹ and to then alert and dispatch searchers for their removal. Sentinels are stationary and capable of detecting intruders within large areas, whereas searchers are mobile and capable of removing the intruders, but their sensing area is much smaller. Both sentinels and searchers are equipped with faulty sensors incurring false alarms and missed detections. We model the problem using an approach based on queueing theory and we characterize the steady state behaviors of the queues using parameters characterizing the agents’ sensors as well as the search strategy implemented by the searchers once dispatched. The derived model provides the basis for addressing various design and analysis questions. For example, we can anticipate the performance of a given composition and configuration of sentinels and searchers when contrasting different temporal and spatial stochastic profiles of intruder attacks. Alternatively, we can determine the optimal size and make-up of a team of sentinels and searchers in order to match a desired performance. Our approach is distributed in the sense that all processing is local to the agents and no information exchange is required. The only communication within the system is from the sentinels to the searchers, i.e., sentinels dispatch searchers when an intrusion is detected but sentinels do not communicate with each other, nor do searchers, respectively. By reducing the amount of exchanged communication and not having a centralized computational center, the resiliency of the system to individual failures increases—a key tenet of distributed robotic systems.

The rest of the paper is organized as follows. Selected related works are discussed in Sect. 2. The formal definition of the problem is given in Sect. 3. The formalization based on queueing theory is given in Sect. 4 and simulations substantiating our findings are presented in Sect. 5. Finally, conclusions and future works are given in Sect. 6.

2 Related Work

Algorithmic models for addressing the proposed patrol problem and its variants have been explored extensively in various communities, including robotics, operations research, and industrial engineering, with operational relevance and significant impact in application areas such as law enforcement, perimeter security, and shipping logistics. Of closest relevance to this paper are formulations of the dynamic vehicle routing problem in relation to algorithmic queuing theory, such as in [3, 8], in which events requiring servicing appear in the environment stochastically, such as random arrivals of intruders in a protected area, requiring one or more agents to prioritize and visit these locations in an online manner. Alternate formulations consider patrol sequences under different assumptions for intruder arrivals, such as cases where intrusion sites are determined according to known probability distributions or by assuming adversarial intruders requiring game-theoretic design of patrols [9]. Commonly used objectives in such patrol problem formulations include minimizing the average or worst case revisit rate to return to a given location, which has correspondence to measures of service rates and wait time in queuing theory models [7, 12]. Other metrics, such as maximized area coverage for sensor deployments [2, 13], enable decentralized control laws to govern persistent surveillance of areas. However, these previous models do not incorporate the possibility of imperfect detections of the events, for which Bayesian methods found in probabilistic search theory [5, 6] provide key insights.

The main theoretical and algorithmic contributions of the proposed work address the challenge of persistently surveilling an area with distributed probabilistic sensors, both fixed and mobile, that are prone to false positive and false negative detections. In addition, this paper highlights insights into the tradeoff in using multi-scale representations of the environment with varying numbers and compositions of such heterogeneous sensors.

3 Problem Definition

We consider the problem of patrolling a planar region using a team of multiple UAVs. We adopt a discretized representation of the environment, namely a regular grid $\mathscr {G}$ composed by k equally sized square cells. Any cell c can be the target of a malicious activity referred as attack. Attacks can be ongoing in one or multiple cells at any given time and only searchers can remove them by performing a clear action. A loss function $l :\mathscr {G} \rightarrow \mathbb {R}_{\ge 0}$ assigns to each cell c a value l(c) which is the cost incurred per unit time while an attack is taking place at cell c.

Given this general background, we define a metric to evaluate the performance of any team of agents independently from their number and their coordination mechanism. Similarly to the metric we introduced in [1], let a(c, t) be a function describing the spatio-temporal realization of attacks, where $a(c,t)=1$ if at time t an attack is present in cell c, and $a(c,t)=0$ otherwise. Without loss of generality, we assume that a patrolling mission starts at time $t = 0$ and ends at time T. We then define our performance metric as:

$$\begin{aligned} \rho (T) = \sum _{c \in \mathscr {G}} l(c) \int _{0}^T a(c,t) d t \end{aligned}$$

(1)

Equation 1 is the sum of k integrals, each measuring the time every cell is under attack (scaled by the loss attributed to the cell). Differently from [1], here we consider continuous time to ease our subsequent theoretical analysis based on queueing theory.

The heterogeneous patrolling team consists of $N = M + R$ agents, with $1 \le M \le |\mathscr {G}|$ and $R \ge M$. M agents are of type sentinel while R are of type searcher. Sentinels are stationary agents which repeatedly scan large portions of the environment for the presence of an attack in that region. When a sentinel observes a positive reading, it dispatches a searcher. Searchers are instead moving agents capable of conducting fine-grained, find–and–clear tasks over some area. Searchers try to localize and clear attacks within the region assigned to the sentinel that dispatched them. In pursuing such task, they will follow some search strategy and will be subject to a finite temporal budget limit. Due to the limited temporal budget and to the use of faulty sensors resulting in missed detections, searchers may fail to detect and remove an intruder present in their assigned area.

The stochastic process of attacks. We consider a situation where the environment is constantly under the threat of attacks which can randomly occur at any time and at any place. We adopt a common assumption from patrolling literature (see, for example, [3]) according to which arrival times for attacks obey a Poisson distribution while their spatial location is determined according to some discrete probability distribution over $\mathscr {G}$. More formally, the inter-arrival time in the whole environment is modeled by an exponential variable with parameter $\lambda$ while the specific cell c is chosen with a probability proportional to the value l(c), i.e., once an attack arrived in the environment, the probability that it will be located at cell c is

$$\begin{aligned} \Pr [c]=\frac{l(c)}{\sum _{m\in \mathscr {G}} l(m)}. \end{aligned}$$

(2)

Once started in a cell c, an attack persists until it is eventually cleared. Note that, based on this model, the same cell may suffer from multiple concurrent attacks.

Defending the environment with sentinels and searchers. Each sentinel i is stationed at a fixed location and is tasked with monitoring a sub-portion of the environment $\mathscr {G}_i \subset \mathscr {G}$. Different assumptions can be made on how sub-portions are defined and where sentinels are positioned. For example, if a Voronoi partition is used, the sentinel could occupy the generator points associated with each partition [2]. Consistent with our sensor model, we adopt a representation based on probabilistic quadtrees [4]. Each sentinel guards a rectangular area $\mathscr {G}_i$, and all $\mathscr {G}_i$s constitute a partition of $\mathscr {G}$ (see Fig. 2 for a visual representation). All areas assigned to the sentinels are equally sized and sentinels are therefore all positioned at the same elevation. With each sensing action, sentinel i obtains a binary reading which, if positive, is interpreted as evidence that at least one attack is currently present in $\mathscr {G}_i$. No additional information is provided for the location of the attack, that is, uniform spatial uncertainty over the cells of $\mathscr {G}_i$ is assumed. With probability $\alpha$, a sentinel receives a positive reading even if no attack is present in its region (false positive), and with probability $\beta$, a negative reading occurs when at least one attack is present (missed detection). Such false positives and missed detection rates depend on the sensor resolution, e.g., defined by the altitude, at which sentinels are located (see [4]). Each sentinel inspects its assigned area for the presence of attacks on a periodic basis every $\varDelta$ time units.

As soon as a sentinel receives a positive detection (whether true or false), a searcher is dispatched over $\mathscr {G}_i$. A searcher’s objective is to find and clear ongoing attacks in that area. To this end, it searches the area to determine which cells within $\mathscr {G}_i$ are under attack. Once a cell c is believed to be under attack above some level of confidence, a clearing action is undertaken. We assume that when such action is performed, if an attack is indeed present, then it is always neutralized. (If more attacks are present, then only the one that has been residing there for the longest time is cleared in a FIFO fashion).

The execution of this task poses the problem of using a patrolling strategy with which a searcher can be driven in the decisions about where to sense next and when to perform clearing actions trying, at the same time, to locally minimize the performance metric. In introducing our two–type based architecture, we opt for searchers driven by deterministic strategies. Such strategies are defined as cyclically repeated paths that scan every cell on a periodic basis. Examples of such strategies are the sweep and the lawn mower patterns [6]. In fact, from a practical perspective these strategies are nowadays still the most widely used in the field. The reason for this restriction to deterministic strategies comes from their relatively simple characterization under statistical terms. This allows us to provide a neat theoretical analysis of our two–type approach, without the cumbersome technicalities that more complex patrolling strategies would have introduced. Such investigations belong outside the scope of this paper and will be the subject of our future research on this problem.

We assume that each searcher is given a time budget B. As soon as such budget is completely consumed, the searcher ends its patrolling mission and returns to the base station. Just like sentinels, each searcher s is equipped with faulty detection sensors whose false positive and missed detection rates are denoted with $\alpha _s$ and $\beta _s$, respectively.

4 Theoretical Analysis

Our eventual objective is to evaluate the loss value defined in Eq. 1 as a function of the various parameters characterizing the system. Inspired by [3], in this section we answer this question relying on queueing theory. The relevant parameters are:

• $\alpha ,\beta$: false positive/missed detection rates by each of the sentinels;

• $\varDelta$: interval between two successive scans by a sentinel;

• A: probability that an attack occurs within the area assigned to the sentinel guarding cell c during an interval of time $\varDelta$;

• $N= 1-A$: probability that no attack occurs;

• $\alpha _s,\beta _s$: false positive/missed detection rates of each of the searchers (in general different than values for the sentinels).

To evaluate the loss, we associate a queue to each cell c and we determine its steady state behavior. This is simpler than modeling all attacks occurring in $\mathscr {G}$ with a single queue. Once the steady behavior of each queue is determined, the overall loss can be evaluated simply adding up the loss accrued in each individual cell. Let $Q_c$ be the queue associated with cell c. Using Kendall’s notation, $Q_c$ can be modeled as a M / G / 1 queue. Note that in general each of the queues is characterized by a different set of parameters. In particular, they will depend on the value l(c). The assumption that the service time is generic (G) stems from the choice of search strategy, i.e., the sweep pattern. Little’s theorem [11] states that the expected number of elements $L_c$ in the $Q_c$ is

$$ L_c = \lambda _c W_c, $$

where $\lambda _c$ is the arrival intensity (number of arrivals per unit time) and $W_c$ is the expected time spent in the queue. Note that this theorem does not rely on Markovian assumptions on the processes, but only on the ergodicity of said stochastic processes and is therefore applicable also for M / G / 1 queues. Once we know $L_c$ for each cell, then through Eq. 1 we can compute the expected aggregate loss. In the following we construct $\lambda _c$ and $W_c$ for the generic queue $Q_c$.

Interarrival time. The process governing the intruders’ spatial and temporal behavior is described in Sect. 3. The interarrival time between two intruders entering the patrolled area is modeled by an exponential variable with parameter $\lambda$, such that the expected interarrival time in the patrolled area is ${1}/{\lambda }$. Upon an intruder’s arrival, it determines the specific cell c to attack according to the mass distribution defined by Eq. 2. The number of attacks necessary before c is attacked is then modeled by a geometric variable with parameter p(c) and its expectation is 1 / p(c). Thus, the expected interarrival time for a specific cell c incorporates both temporal and spatial components, given by

$$\begin{aligned} T_c = \frac{1}{\lambda }\frac{1}{p(c)} \end{aligned}$$

(3)

and the arrival intensity for cell $Q_c$ is then $\lambda _c = \lambda p(c)$.

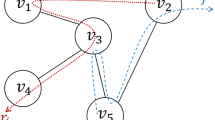
Service time. We next need to determine $W_c$, i.e., the expected time spent in $Q_c$ by an intruder. Figure 1 depicts the most general case that helps in understanding the structure of the random variable $w_c$, modeling the time spent by an intruder before it is removed.

Fig. 1

Elements contributing to the time $w_c$ between the arrival and removal of an intruder

The sentinel queries its sensor at a fixed frequency and once a searcher is dispatched to the area, it may or may not find all intruders. $w_c$ is then the sum of various components. The first component, $\zeta$, is the time elapsed between when the intruder arrives in cell c (and then enters $Q_c$) and the first time the sentinel scans the area including c. In general it may take more than one scan before a searcher is dispatched. This time is given by the variable $t_{tr}$ (time to trigger) and by construction, a multiple of $\varDelta$. After a searcher is dispatched, it will not necessarily find the intruder, so in general multiple successive, independent searchers have to be dispatched. Then, $t_{tr}^i$ is the time to trigger the dispatch of the ith searcher. Once the successful searcher is dispatched, it spends time s before it finds the intruder. Therefore,

$$ w_c = \zeta + \sum _{i=1}^{n_s} t_{tr}^i + s $$

where $n_s$, the number of dispatched searchers, is also a random variable. As it will be explained later on, the various $t_{tr}^i$ are all independent but not all equally distributed. In particular, $t_{tr}^1$ has a distribution different from the following ones, whereas all the $t_{tr}^j$ with $j \ge 2$ are i.i.d. Keeping this in mind, we can then write

$$\begin{aligned} W_c = \mathbb {E}[w_c] = \mathbb {E}[\zeta ] + \mathbb {E}[t_{tr}^1]+(\mathbb {E}[n_s]-1)\mathbb {E}[t_{tr}] + \mathbb {E}[s]. \end{aligned}$$

(4)

Let us start with computing $N_s = \mathbb {E}[n_s]$. Each searcher follows a deterministic search strategy with a finite time budget. During this search each cell is inspected the same number of times, say m. The missed detection error rate is $\beta _s$, so a searcher fails to find the intruder located in c with probability $\beta _s^m$, and finds it with probability $1-\beta _s^m$. The number of searchers, $n_s$, needed to detect the intruder is then modeled by a geometric variable with parameter $1-\beta _s^m$ and its expectation is $\mathbb {E}[n_s]=\frac{1}{1-\beta _s^m}$.

Next, we determine $S=\mathbb {E}[s]$ conditioned on the event that the searcher finds the intruder. Given that the searcher follows a predetermined path unrelated to l(c), assuming that the search time budget is B, then $S={B}/{2}$ because the intruder could be located with equal probability in any of the sequentially scanned cells.

To determine $Z = \mathbb {E}[\zeta ]$, it is useful to recall that the interarrival time of $Q_c$ and then of the intrusions to cell c is modeled by an exponential variable of parameter $\lambda _c = \lambda p(c)$. Due to the memoryless property of exponential random variables and its basic properties, it follows that $\zeta = \varDelta - y$, where y is an exponential random variable of parameter $\lambda _c$ conditioned on the event $y \le \varDelta$. Through algebraic manipulation and applying the definition of expectation one obtains

$$ \mathbb {E}[\zeta ] = \mathbb {E}[\varDelta - y] = \varDelta - \mathbb {E}[y]=\varDelta - \frac{1-e^{-\lambda _c \varDelta }-\lambda _c\varDelta e^{-\lambda _c \varDelta }}{\lambda _c (1-e^{-\lambda _c\varDelta })} $$

Finally, it is necessary to compute $\mathbb {E}[t_{tr}^1]$ and $\mathbb {E}[t_{tr}^j]$ with $j>1$. Recalling that $t_{tr}^i$ is an integer multiple of $\varDelta$, i.e., $t_{tr}^i = K\varDelta$, it is then sufficient to compute the mass distribution of the multiplicative factor K for the two different cases. K is the number of times the sentinel has to sense before a searcher is dispatched. It is useful to recall that $t_{tr}^1$ models the time to trigger the dispatch of the first searcher conditioned on the fact that one intruder entered the area assigned to the sentinel (see Fig. 1). Its mass distribution is

$$\begin{aligned} \Pr [K=k] = {\left\{ \begin{array}{ll} (1-\beta ) &{} k=1 \\ \beta (A\beta +N(1-\alpha ))^{k-2}(N\alpha + A(1-\beta )) &{} k \ge 2 \end{array}\right. } \end{aligned}$$

(5)

The rationale behind the formula is the following. $K=1$ if the intruder generates a detection by the sentinel the first time the sentinel senses the area. This is by definition $1-\beta$. Otherwise, conditioned on the fact that an intruder entered cell c, the first searcher will be triggered after $k\ge 2$ scans as a consequence of the simultaneous occurrence of the following independent events:

• the intruder is not detected, which has probability $\beta$;

• for $k-2$ steps there was not detection. Since each step is independent from each other, we can just raise to the power of $k-2$ the probability that no detection occurred in one step. This event is either due to an attack going undetected, whose probability is $A\beta$ or a non-attack not generating a false positive (probability $N(1-\alpha )$). Note that these two events are mutually exclusive (either an attack happens or it does not), so we can just add the probabilities together.

• at the last step a detection happens. This is either due to a non-attack generating a false positive (probability $N\alpha$) or an attack being detected (probability $A(1-\beta )$).

We seek an expression for the mass distribution for $t_{tr}^j$, i.e., the time to trigger the jth searcher ($j > 1$) conditioned on the fact that the first searcher has already been dispatched. This variable is a geometric random variable, and its distribution is then:

$$ \Pr [K=k] = (N(1-\alpha )+A\beta )^{k-1}(A(1-\beta )+N\alpha ). $$

The rationale to derive this formula is similar to the one for $t_{tr}^1$ and one should also notice that it is indeed a geometric variable because $N(1-\alpha )+A\beta + A(1-\beta )+N\alpha =1$. To complete the computation of Eq. 4 we need to compute $\mathbb {E}[t_{tr}^1]$ and $\mathbb {E}[t_{tr}]$. Skipping the algebraic details in the interest of space, we just give the results, i.e.,

$$ \mathbb {E}[t_{tr}^1] = 1-\beta + \frac{\beta }{1-N\alpha - A(1-\beta )} \qquad \mathbb {E}[t_{tr}] = \frac{1}{1-A(1-\beta )+N\alpha }. $$

We conclude this section noting that A and N can be easily determined from knowledge of the set of cells covered by the sentinel guarding cell c.

5 Simulations

In this section, we provide experimental analysis for empirical assessment of some of the properties of the proposed two-type approach. We analyze performance in terms of accrued loss (per Eq. (1)), required costs in terms of number of deployed sentinels and frequency of sampling for each of them, and we look at how the system responds under different loads expressed by variable attack arrival rates.

Our basic experimental setting builds on top of the in-the-field validation conducted in [4] with the aim of maintaining relevance to realistic deployments of UAVs. The grid $\mathscr {G}$ consists of $16 \times 16$ cells and two different loss functions are considered: a simple uniform loss (UNI) that assigns equal loss to every cell and a bimodal one (BI) depicted in Fig. 2a. The arrival rate for attacks is $\lambda = 1/95$.

We consider three different groups of sentinels of cardinality 1, 4, and 16 uniformly deployed in the environment (see Fig. 2b, c). That is, if h sentinels are present, then their equally sized assigned areas $\mathscr {G}_i$ constitute a partition of $\mathscr {G}$. The sampling period for each sentinel is given by $\varDelta = L/4$, where L is the time a searcher would require to scan and clear every cell of its area by following some deterministic strategy. Error rates are chosen as a function of the altitude and, to account for the fact they are tailored for constant altitude, we scaled by a $\frac{1}{2}$ factor, that is $\alpha ^{1}=0.43/2$, $\beta ^{1}=0.38/2$, $\alpha ^{4}=0.36/2$, $\beta ^{4}=0.27/2$, $\alpha ^{16}=0.35/2$, $\beta ^{16}=0.37/2$ where $\alpha ^h$ and $\beta ^h$ refer to the error rates when having a deployment of h sentinels. These error rates, as well as those for the searchers given in the following, were determined from extensive live-fly experiments presented in [4].

Fig. 2

Bimodal loss function and deployments of multiple sentinels. a Bimodal loss. b Deployment of 4 sentinels. c Deployment of 16 sentinels

Searchers conduct a deterministic sweep pattern, sequentially scanning every cell per unit time on the sub-grid associated to that area. False positives and missed detections are chosen according to their altitude value (the lowest in a quadtree built over a $16 \times 16$ grid) as $\alpha _s=0.09$ and $\beta _s=0.05$. We assume that flying from a cell to an adjacent one, scanning that cell, and performing a clear action on the cell each take a single time unit. As a consequence, scanning and clearing every cell of a sub-grid $\mathscr {G}'$ takes $L=3|\mathscr {G}'|$ time units. We also define the temporal budget of each searcher w.r.t. this quantity as $B=mL$, where m is an integer value. In the results presented here, we fix $m=2$, that is, once dispatched, each searcher must always perform at least two whole sweeps of the assigned area. Finally, we assume to have an unbounded number of searchers, namely every dispatch is immediately executed. Studying the situation where the number of searchers is bounded is left for future work, although as evidenced in this section, the number of concurrently active searchers remains limited.

Fig. 3

Total loss accrued during missions for varying number of sentinels for different loss functions

Figure 3 reports average results obtained for an experimental design of 20 random missions. (Each run corresponds to a different realization of the attacks arrival process.) Graph 3a, b show how the average accrued loss evolves as the mission unfolds and as sentinels sense their areas every scan period k.

By inspecting these graphs, we can empirically assess the extent of two expected trends in the actual performance achieved by the different teams. The first observation is that having more sentinels leads to a smaller loss whose reduction is nearly optimal when employing 16 sentinels. One interesting feature can be observed in Fig. 3c where the ratios between single-sentinel and 4-sentinel loss as well as between 4-sentinels and 16-sentinels are depicted (bimodal loss is considered here). The first thing we notice is that even if we increase our resources by a factor of 4, we observe (mostly at every mission time) gains of much higher order (${\ge }10$). The reason is that, besides merely having more sentinels we are also introducing two improvement factors, which indirectly come by construction of our framework: (1) not only are sentinels greater in number but also are each more accurate in sensing, since they operate at lower altitudes; (2) the more sentinels are employed, the more effectively the environment is split for parallel patrolling missions (for any loss function). This second factor contributes to the other observed trend, that is, passing from 4 to 16 sentinels is never worse than increasing from 1 to 4. Indeed, when deploying 16 sentinel we get a critical split of an highly targeted sub-area of the environment (recall Fig. 2).

Moreover, from Graph 3a, b we can see how a bimodal loss function results in poorer performance, showing the disadvantage of adopting a uniform spatial deployment over a non-uniform loss distribution.

An interesting operational metric is given by the load factor of each sentinel, defined as the ratio between the total number of attacks still present in the environment over the number of searchers that have been dispatched by that sentinel and did not use up their respective time budgets. Figure 4a, b compare average factors for the 1-sentinel and 4-sentinels cases as the mission evolves (the curve in Fig. 4b depicts the average load factor over the four sentinels). The 1-sentinel case reported an overall average load of 28 %, whereas, as it can be seen, different mission times experienced an overload condition (load factor greater than one) with attacks outnumbering searchers. Such situation is not observed when employing four sentinels, and the overall average factors for each sentinel resulted to be remarkably lower. Such results experimentally highlight the improvements obtained from the partitioning of the search area, w.r.t. a metric which is independent from the loss function, i.e., the importance level assigned to every cell in the grid.

Fig. 4

Load factors and accrued loss with different scan periods durations. a 1 Sentinel. b 4 Sentinel. c Loss w.r.t. scan period

The number of sentinels constitutes the primary measure of cost in our setting. Another important cost factor is given by the number of employed searchers or, equivalently, the number of dispatches. Given the assumption of an unbounded R, we can control such cost via the sentinels scanning period $\varDelta$, with the obvious expectation that the more frequently sentinels scan the more dispatches they will likely issue. Figure 4c shows how reducing costs of this type can introduce a decrease in performance. Starting from our reference value of $\varDelta$, we scale it by increasing integer factors and we measure the total loss accrued at the end of the mission. As can be seen, the 1-sentinel case is where longer scan periods are more critical. On the contrary, situations with multiple sentinels (e.g., the case of four sentinels included in the graph) seem to be more robust with a relatively graceful degradation in performance.

Fig. 5

Number of active searchers and attacks with different arrival rates. a 100$\lambda$. b 60$\lambda$. c 20$\lambda$

For further experimental validation, we assess how the system responds to increasing attack arrival rates by showing in Fig. 5 how the number of active searchers and attacks vary during the mission under arrival rates obtained by scaling our reference $\lambda$. The observed trend is that for very high arrival rates, the number of attacks almost always exceeds the number of active searchers for each sentinel. (Note that the number of attacks is the per-sentinel average where an attack is associated to a sentinel if it occupies a cell in that sentinel’s area.)

In our final experiment we assess the sensitivity of our model to the parameters characterizing the stochastic model of attacks. In particular, we focus on the interarrival times. Our analysis stands on the assumption that these random variables are i.i.d and follow an exponential distribution with known parameter $\lambda$. In our last test we change this distribution with a different one having the same expectation. This choice is motivated from practical considerations. When building a model of the opponent through repeated observations, experimentally observing the expected interarrival time is the simplest first step, but there are evidently multiple distributions that can fit the data. In this experiment, we select a uniform distribution. Figure 6 plots the difference between the performance of the system under two different scenarios. In the first case interarrival times are distributed according to an exponential distribution and then match the model we used in deriving our analysis. In the second case interarrival times are uniformly distributed, but now incorrectly modeled. As we did for Fig. 3a, we vary the number of sentinels (one or four) and consider two different loss models (unimodal or bimodal), thus obtaining four different curves. The figure shows that when considering four sentinels, differences in performance are negligible. When a single sentinel is considered, a difference, albeit limited, is observed. To put the magnitude of the difference into perspective, the reader is referred to Fig. 3a for absolute loss values. Given that in general one will use multiple sentinels, these findings tend to indicate that the model is robust to identification errors for interarrival times.

Fig. 6

Difference in accrued loss when interarrival times arrivals are exponentially distributed or uniformly distributed

6 Conclusions

In this paper we have studied a patrolling problem using two classes of agents, namely sentinels and searchers. The setup is inspired from our recent work in a single-agent setting and our model is driven by experimental data collected through extensive live-fly experiments. Using analytic formulations founded on queueing theory, it is possible to determine how the system behaves asymptotically in response to different stochastic models of arrivals. Studies in simulation show how explicitly modeling a variable resolution sensor leads to gains outweighing the potential penalty of increasing the number of allocated sentinels.

Future work include extensions explicitly handling deconfliction and coordination among searchers, as well as deploying sentinels with overlapping regions for increased robustness and performance. Additional research addresses further theoretical analysis of the impact of constrained resources (e.g., number of searchers available to sentinels), with relevance to realistic deployments. Finally, building upon the analysis we developed, we will consider how to non-uniformly allocate sentinels in the environment in order to minimize the given performance metrics. This includes positioning more sentinels to cover areas with higher loss values, as well as varying their elevation to operate in regimes with lower error rates where needed.