Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Single and coaxial shells of revolution are the integral parts of many technological applications and while in operation can interact with the axial and rotational fluid flows occurring simultaneously. There are a lot of papers in the literature [1], in which the authors based on the numerical and experimental investigations have come to a conclusion that the axial flow of a fluid as well as its rotation exerts a destabilizing effect. However, as far as we know there have been practically no investigations dealing with their combined action on the stability boundary. In this paper we discuss a numerical method of solving this problem. The numerical experiments made for this study allow us to determine a relationship between the dynamic behavior of cantilevered single and coaxial shells and their linear dimensions as well as the width of the annular space between the inner and outer shells.

2 Statement of the Problem and Constitutive Relations

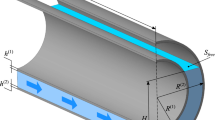
Let us consider two elastic coaxial cylindrical shells of length L (Fig. 1). The inner shell has radius a, and the outer shell has radius b. The shells are subject to two flows of ideal compressible fluids: one occurring inside the inner shell and the other – in the annular gap between the shells. A single shell in the problem formulation considered in this paper can be treated as a particular case. The axial velocity of the internal flow, its angular velocity, specific density and sound speed are denoted by U i , Ω i , \(\varrho _{f}^{i}\) and c i , respectively. The corresponding parameters of the annular flow are denoted by the same symbols, in which the subscript i is replaced by o. It is necessary to find such a combination of the axial and angular velocity components of the fluid flow, at which the elastic body will lose stability.

The motion of an ideal compressible fluid in the case of potential flow is described by the wave equation, which for the internal flow, occupying volume \(V _{j}^{i}\), can be written in the cylindrical coordinate (r, θ, x) as [2]

$$\displaystyle\begin{array}{rcl} & {\nabla }^{2}\phi _{i}& - \frac{1} {c_{i}^{2}}{\left [ \frac{\partial } {\partial t} + U_{i} \frac{\partial } {\partial x}\right ]}^{2}\phi _{ i} = \\ & & = \frac{2\varOmega _{i}} {c_{i}}\left (M_{i} \frac{{\partial }^{2}\phi _{i}} {\partial x\partial \theta } + \frac{1} {c_{i}} \frac{{\partial }^{2}\phi _{i}} {\partial \theta \partial t}\right ) + \frac{\varOmega _{i}^{2}} {c_{i}^{2}}\left (\frac{{\partial }^{2}\phi _{i}} {{\partial \theta }^{2}} - r \frac{\partial \phi _{i}} {\partial r}\right ),{}\end{array}$$
(1)

where ϕ is the perturbation velocity potential, \(M_{i}\,=\,U_{i}/c_{i}\) is the Mach number. The pressure exerted by the internal fluid flow p i on the interface between the inner shell and the fluid \(S_{\sigma }^{i}\) is calculated by the linearized Bernoulli formula

$$\displaystyle{ p_{i} = -\varrho _{f}^{i}\left (\frac{\partial \phi _{i}} {\partial t} + U_{i} \frac{\partial \phi _{i}} {\partial s} +\varOmega _{i}\frac{\partial \phi _{i}} {\partial \theta } \right ). }$$
(2)

The equations for the annular flow are similar to, (1)–(2) with the only difference that the subscript i is replaced by o. The interface between the inner shell and internal flow \(S_{\sigma }^{i}\) must satisfy the impermeability condition

$$\displaystyle{ \frac{\partial \phi _{i}} {\partial r} = \frac{\partial w_{i}} {\partial t} + U_{i}\frac{\partial w_{i}} {\partial s} +\varOmega _{i}\frac{\partial w_{i}} {\partial \theta }. }$$
(3)

The conditions imposed on the inner shell-annular flow interface \(S_{\sigma }^{io}\) and the outer shell-annular flow interface \(S_{\sigma }^{o}\) are written as

$$\displaystyle\begin{array}{rcl} \frac{\partial \phi _{o}} {\partial r}& =& \frac{\partial w_{i}} {\partial t} + U_{o}\frac{\partial w_{i}} {\partial s} +\varOmega _{o}\frac{\partial w_{i}} {\partial \theta },{}\end{array}$$
(4)
$$\displaystyle\begin{array}{rcl} \frac{\partial \phi _{o}} {\partial r}& =& \frac{\partial w_{o}} {\partial t} + U_{o}\frac{\partial w_{o}} {\partial s} +\varOmega _{o}\frac{\partial w_{o}} {\partial \theta }.{}\end{array}$$
(5)

Here w i and w o are the normal components of the displacement vector of the inner and outer shells. The inlet and outlet perturbation velocity potentials are subject to the following boundary conditions

$$\displaystyle{ x = 0: \phi _{i} =\phi _{o} = 0\;,\qquad x = L: \frac{\partial \phi _{i}} {\partial x} = \frac{\partial \phi _{o}} {\partial x} = 0\;. }$$
(6)

For numerical implementation of the problem based on the semi-analytical version of the finite element method the equations for perturbation velocity potential (1) together with the boundary conditions (3)–(6) should be transformed using the Bubnov-Galerkin method [3].

Fig. 1
figure 1

Computational scheme

Full size image

The model equations of shells considered in this paper are derived by accepting the Kirchhoff-Love hypothesis, according to which the components of the strain vector of the middle surface and the curvature and torsion changes written in the coordinate system (s, θ, z) are given as [4]

$$\displaystyle\begin{array}{rcl} \varepsilon _{1}^{i}& =& \frac{\partial u_{i}} {\partial s},\quad \varepsilon _{2}^{i} = \frac{1} {a}\left (\frac{\partial v_{i}} {\partial \theta } + w_{i}\right ),\quad \varepsilon _{12}^{i} = \frac{1} {a} \frac{\partial u_{i}} {\partial \theta } + \frac{\partial v_{i}} {\partial s}, \\ \kappa _{1}^{i}& =& -\frac{{\partial }^{2}w_{ i}} {\partial {s}^{2}},\quad \kappa _{2}^{i} = \frac{1} {{a}^{2}}\left (\frac{\partial v_{i}} {\partial \theta } -\frac{{\partial }^{2}w_{i}} {{\partial \theta }^{2}} \right ),\quad \kappa _{12}^{i} = \frac{1} {a}\left (\frac{\partial v_{i}} {\partial s} -\frac{{\partial }^{2}w_{i}} {\partial s\partial \theta } \right ).\quad \,\,\,\,{}\end{array}$$
(7)

Here u i and v i are the meridional and circumferential components of the displacement vector of the inner shell.

The physical equations relating the vector of generalized forces and moments T i to the vector of the generalized strains \(\boldsymbol{\varepsilon }_{i} ={ \left \{\varepsilon _{1}^{i},\varepsilon _{2}^{i},\varepsilon _{12}^{i},\kappa _{1}^{i},\kappa _{2}^{i},2\kappa _{12}^{i}\right \}}^{\mathrm{T}}\) can be represented in the matrix form

$$\displaystyle{ \mathbf{T}_{i} ={ \left \{T_{11}^{i},T_{ 22}^{i},T_{ 12}^{i},M_{ 11}^{i},M_{ 22}^{i},M_{ 12}^{i}\right \}}^{\mathrm{T}} = \mathsf{D}_{ i}\boldsymbol{\varepsilon }_{i}, }$$
(8)

where the non-zero matrix elements \(\mathsf{D}_{i}\) for an isotropic material are conventionally defined in terms of the elasticity modulus E i and Poisson’s ratio ν i .

The mathematical description of the dynamic behavior of the shells is based on the virtual displacement principle, which for the inner shell can be written in the matrix form as

$$\displaystyle{ \int \limits _{S_{i}}\delta \boldsymbol{\varepsilon }_{i}^{\mathrm{T}}\mathbf{T}_{ i}\mathit{dS} +\int \limits _{S_{i}}\delta \mathbf{d}_{i}^{\mathrm{T}}\varrho _{ 0}^{i}\ddot{\mathbf{d}}_{ i}\mathit{dS} -\int \limits _{S_{i}}\delta \mathbf{d}_{i}^{\mathrm{T}}\mathbf{P}_{ i}\mathit{dS} = 0. }$$
(9)

Here d i and \(\mathbf{P}_{i} ={ \left \{\begin{array}{ccc} 0\;&0\;&p_{i}\vert _{r=a} - p_{o}\vert _{r=a} \end{array} \right \}}^{\mathrm{T}}\) are the vectors of the generalized displacements and surface loads, \(\rho _{0}^{i} =\int \limits _{h_{i}}\varrho _{s}^{i}\mathit{dz}\), \(\varrho _{s}^{i}\) is the specific density of the material of the inner shell, h i is the thickness of the inner shell. An analogous equation (where i is replaced by o) is written for the outer shell, for which \(\mathbf{P}_{o} =\{{ \begin{array}{ccc} 0\;&0\;&p_{o}\vert _{r=b} \end{array} \}}^{\mathrm{T}}\).

Applying the standard finite element procedures and representing the perturbed motion of the shell and the fluid as \(\left (\mathbf{d}_{i},\boldsymbol{\phi }_{i},\mathbf{d}_{o},\boldsymbol{\phi }_{o}\right ) = \left (\mathbf{q}_{i},\mathbf{f}_{i},\mathbf{q}_{o},\mathbf{f}_{o}\right )\exp (\mathrm{i}\lambda t)\), we obtains the systems of equations, which can be combined into one expression

$$\displaystyle{ \left (\mathsf{K} + \mathsf{A} {-\lambda }^{2}\mathsf{M} + \mathrm{i}\lambda \mathsf{C}\right ){\left \{\mathbf{q}_{ i},\mathbf{f}_{i},\mathbf{q}_{o},\mathbf{f}_{o}\right \}}^{\mathrm{T}} = 0, }$$
(10)

where

$$\displaystyle\begin{array}{rcl} \begin{array}{lcl} \mathsf{K} & =&\mathrm{diag}\left \{\mathsf{K}_{s}^{i},\mathsf{K}_{f}^{i} + \mathsf{K}_{f}^{\omega i},\mathsf{K}_{s}^{o},\mathsf{K}_{f}^{o} + \mathsf{K}_{f}^{\omega o}\right \},\\ && \\ \mathsf{M}& =&\mathrm{diag}\left \{\mathsf{M}_{s}^{i},\mathsf{M}_{f}^{i},\mathsf{M}_{s}^{o},\mathsf{M}_{f}^{o}\right \},\end{array} & & {}\\ & & \mathsf{C} = \left [\begin{array}{*{20}{c}} 0 & \mathsf{C}_{\mathit{sf }}^{i} & 0 & \mathsf{C}_{\mathit{sf }}^{o} \\ \mathsf{C}_{\mathit{fs}}^{i} &\mathsf{C}_{f}^{\mathit{ci}} + \mathsf{C}_{f}^{\omega i}& 0 & 0 \\ 0 & 0 & 0 & \mathsf{C}_{\mathit{sf }}^{o} \\ \mathsf{C}_{\mathit{fs}}^{o}& 0 &\mathsf{C}_{\mathit{fs}}^{o}&\mathsf{C}_{f}^{\mathit{co}} + \mathsf{C}_{f}^{\omega o} \end{array} \right ], {}\\ & & {}\\ & & \mathsf{A} = \left [\begin{array}{*{20}{c}} 0 &\mathsf{A}_{\mathit{sf }}^{i} + \mathsf{A}_{\mathit{sf }}^{\omega i}& 0 &\mathsf{A}_{\mathit{sf }}^{o} + \mathsf{A}_{\mathit{sf }}^{\omega o} \\ \mathsf{A}_{\mathit{fs}}^{i} + \mathsf{A}_{\mathit{fs}}^{\omega i} & \mathsf{A}_{f}^{\mathit{ci}} + \mathsf{A}_{f}^{\omega i} & 0 & 0 \\ 0 & 0 & 0 &\mathsf{A}_{\mathit{sf }}^{o} + \mathsf{A}_{\mathit{sf }}^{\omega o} \\ \mathsf{A}_{\mathit{fs}}^{o} + \mathsf{A}_{\mathit{fs}}^{\omega o}& 0 &\mathsf{A}_{\mathit{fs}}^{o} + \mathsf{A}_{\mathit{fs}}^{\omega o}& \mathsf{A}_{f}^{\mathit{co}} + \mathsf{A}_{f}^{\omega o} \end{array} \right ],{}\\ \end{array}$$
$$\displaystyle\begin{array}{rcl} & & \mathsf{K}_{s}^{i} =\sum \limits _{ m_{s}^{i}}\int \limits _{S_{s}^{i}}\mathsf{B}_{i}^{\mathrm{T}}\mathsf{D}_{ i}\mathsf{B}_{i}\mathit{dS},\;\mathsf{M}_{s}^{i} =\sum \limits _{ m_{s}^{i}}\int \limits _{S_{s}^{i}}\mathsf{N}_{i}^{\mathrm{T}}\varrho _{ 0}^{i}\mathsf{N}_{ i}\mathit{dS},\;\mathsf{A}_{\mathit{sf }}^{i} =\sum \limits _{ m_{s}^{i}}\int \limits _{S_{\sigma }^{i}}\varrho _{f}^{i}U_{ i}\mathsf{\bar{N}}_{i}^{\mathrm{T}}\frac{\partial \mathsf{F}_{i}} {\partial s} \mathit{dS}, {}\\ & & \mathsf{K}_{f}^{i} =\sum \limits _{ m_{f}^{i}}\int \limits _{V _{f}^{i}}\left (\frac{\partial \mathsf{F}_{i}^{\mathrm{T}}} {\partial r} \frac{\partial \mathsf{F}_{i}} {\partial r} + \frac{1} {{r}^{2}} \frac{\partial \mathsf{F}_{i}^{\mathrm{T}}} {\partial \theta } \frac{\partial \mathsf{F}_{i}} {\partial \theta } + \frac{\partial \mathsf{F}_{i}^{\mathrm{T}}} {\partial x} \frac{\partial \mathsf{F}_{i}} {\partial x} \right )\mathit{dV },\;\mathsf{M}_{f}^{i} =\sum \limits _{ m_{f}^{i}}\int \limits _{V _{f}^{i}} \frac{1} {c_{i}^{2}}\mathsf{F}_{i}^{\mathrm{T}}\mathsf{F}_{ i}\mathit{dV },{}\\ \end{array}$$
$$\displaystyle\begin{array}{rcl} & & \mathsf{C}_{\mathit{fs}}^{i} = -\sum \limits _{ m_{s}^{i}}\int \limits _{S_{\sigma }^{i}}\mathsf{F}_{i}^{\mathrm{T}}\mathsf{\bar{N}}_{ i}\mathit{dS},\;\mathsf{C}_{f}^{\mathit{ci}} =\sum \limits _{ m_{f}^{i}}\int \limits _{V _{f}^{i}}\frac{2U_{i}} {c_{i}^{2}} \frac{\partial \mathsf{F}_{i}^{\mathrm{T}}} {\partial x} \mathsf{F}_{i}\mathit{dV },\;\mathsf{A}_{f}^{\mathit{ci}} = -\sum \limits _{ m_{f}^{i}}\int \limits _{V _{f}^{i}}M_{i}^{2}\frac{\partial \mathsf{F}_{i}^{\mathrm{T}}} {\partial s} \frac{\partial \mathsf{F}_{i}} {\partial s} \mathit{dV }, {}\\ & & \mathsf{A}_{\mathit{fs}}^{i} = -\sum \limits _{ m_{s}^{i}}\int \limits _{S_{\sigma }^{i}}U_{i}\mathsf{F}_{i}^{\mathrm{T}}\frac{\partial \mathsf{\bar{N}}_{i}} {\partial s} \mathit{dS},\;\mathsf{C}_{\mathit{sf }}^{i} =\sum \limits _{ m_{s}^{i}}\int \limits _{S_{\sigma }^{i}}\varrho _{f}^{i}\mathsf{\bar{N}}_{ i}^{\mathrm{T}}\mathsf{F}_{ i}\mathit{dS},\;\mathsf{A}_{\mathit{fs}}^{\omega i} =\sum \limits _{ m_{f}^{i}}\int \limits _{S_{\sigma }^{i}}\varOmega _{i}\frac{\partial \mathsf{\bar{N}}_{i}} {\partial \theta } \mathsf{F}_{i}\mathit{dS}, {}\\ & & \mathsf{K}_{f}^{\omega i} =\sum \limits _{ m_{f}^{i}}\int \limits _{V _{f}^{i}} \frac{\varOmega _{i}^{2}} {c_{i}^{2}}\left [\frac{{\partial }^{2}\mathsf{F}_{i}^{\mathrm{T}}} {{\partial \theta }^{2}} \mathsf{F}_{i} - r\frac{\partial \mathsf{F}_{i}^{\mathrm{T}}} {\partial r} \mathsf{F}_{i}\right ]\mathit{dV },\;\mathsf{C}_{f}^{\omega i} = -\sum \limits _{ m_{f}^{i}}\int \limits _{V _{f}^{i}} \frac{2\varOmega _{i}} {c_{i}^{2}} \frac{\partial \mathsf{F}_{i}^{\mathrm{T}}} {\partial \theta } \mathsf{F}_{i}\mathit{dV }, {}\\ & & \mathsf{A}_{\mathit{sf }}^{\omega i} =\sum \limits _{ m_{s}^{i}}\int \limits _{S_{\sigma }^{i}}\varrho _{f}^{i}\varOmega _{ i}\mathsf{\bar{N}}_{i}^{\mathrm{T}}\frac{\partial \mathsf{F}_{i}} {\partial \theta } \mathit{dS},\;\mathsf{A}_{f}^{\omega i} =\sum \limits _{ m_{f}^{i}}\int \limits _{V _{f}^{i}}2\varOmega _{i}\frac{M_{i}} {c_{i}} \frac{{\partial }^{2}\mathsf{F}_{i}^{\mathrm{T}}} {\partial x\partial \theta } \mathsf{F}_{i}\mathit{dS}. {}\\ \end{array}$$

Here \(\mathsf{B}_{i}\) is the matrix relating the strain vector \(\boldsymbol{\varepsilon }_{i}\) to the vector of nodal displacements of the shell-type finite element; \(m_{f}^{i}\) and \(m_{s}^{i}\) is the number of finite elements used to decompose the fluid domain \(V _{f}^{i}\) and the inner shell domain \(V _{s}^{i}\); \(\mathsf{F}_{i}\), \(\mathsf{N}_{i}\), \(\mathsf{\bar{N}}_{i}\) are the shape functions for the perturbation velocity potential of the internal flow, the shell-type element and the normal component of the inner shell displacement vector; \(\mathbf{q}_{i}\), f i , q o , f o are some functions of the coordinates; \({\mathrm{i}}^{2} = -1\); \(\lambda =\lambda _{1} + \mathrm{i}\lambda _{2}\) is the characteristic number. Missing matrices can be obtained by replacing the index i by the index o.

Problem solving is reduced to the computation and analysis of the eigenvalues of system (10). Complex eigenvalues are calculated by the algorithm based on the Müller method [5]. To maximize the computational efficiency of the algorithm, the degree of freedom of system (10) was renumbered using the reverse Cuthill-McKee algorithm [6].

3 Results of Computations

The computations discussed below were made for different values of the width of the annular gap between the outer and inner shells, which is defined by the following relation: \(k = (b - a)/a\). Here we present several examples of numerical simulation for a cylindrical shell (\(E = 2 \times 1{0}^{11}N/{m}^{2}\), ν = 0. 29, \(\varrho _{s} = 7,812\,\mathrm{{kg/m}}^{3}\), \(R = 1\,\mathrm{m}\), \(h = 0.01\,\mathrm{m}\)) and a system of coaxial shells (\(E_{i} = E_{o} = 2 \times 1{0}^{11}N/{m}^{2}\), \(\nu _{i} =\nu _{o} = 0.3\), \(\varrho _{s}^{i} =\varrho _{ s}^{o} = 7,800\,\mathrm{kg/{m}^{3}}\), \(L = 1\,\mathrm{m}\), \(b = 0.1\,\mathrm{m}\), \(h_{i} = h_{o} = 5 \times 1{0}^{-4}\,\mathrm{m}\)), simply supported (\(v = w = 0\)) at both ends (x = 0, L) or supported as a cantilever. The shells are subject to a compressible fluid \(\varrho _{f}^{i} =\varrho _{ f}^{o} = 1{0}^{3}{\mathrm{kg/m}}^{3}\), \(c_{i} = c_{o} = 1,500\,\mathrm{m/s}\). In all calculations we used 40 elements for each shell and 1,000 and 1,600 elements for the fluid in a single shell and coaxial shell, respectively. In the latter case the number of elements was defined by the width of the space between the shells.

The numerical experiments have shown that under the combined action of simultaneous axial and rotational fluid flows the shells lose stability. The type of stability loss is determined by the boundary conditions. In particular, the dependence of the eigenvalues λ(Hz) on the axial velocity of the fluid U(m/s) was obtained for single shells of revolution, in which the axial and rotational flows with the angular velocity Ω = 50 rad/s (Fig. 2) occur concurrently. In the figure, the dashed lines denote eigenvalues, corresponding to the backward waves, and solid lines denote eigenvalues, corresponding to the forward waves. The results of computation show that for shells simply supported (Fig. 2a) or clamped at both ends, the loss of stability occurs in the form of a coupled-mode flutter, since at the axial flow velocity U CF the real parts of the forward and backward waves of the first mode (m = 1) coalesce. For cantilevered shells (Fig. 2b) the loss of stability occurs in the form of a single-mode flutter, at which the imaginary part of the third mode for the fluid velocity U SF becomes negative.

Fig. 2
figure 2

The real and imaginary parts (a) and loci (b) of eigenvalues (Hz) versus axial velocity component of the rotating flow U: (a) simply supported shell; (b) cantilevered shell

Full size image
Fig. 3
figure 3

Stability diagram for simply supported (a) and cantilevered (b) shells having different linear dimensions L∕R

Full size image

Figure 3 shows the stability diagrams obtained in the case of combined action of both velocity components for single shells under different boundary conditions and having different linear dimensions L∕R (the number of the harmonic in the circumferential direction is j = 4). From the results shown in Fig. 3b it can be concluded that for cantilevered shells the axial velocity component has a stabilizing effect, which strongly depends on the linear dimensions of the system – the smaller dimensions the higher is the stability boundary. With increasing L∕R the stabilizing effect of the axial velocity vanishes.

Figure 4 shows the stability boundaries obtained for coaxial shells for different variants of the boundary conditions and different values of the annular gap width (j = 3). In this case, for cantilevered shells the axial fluid flow also exerts a stabilizing effect, whereas for shells with other boundary conditions it has only a destabilizing effect. The strength of the stabilizing effect depends on the width of the annular gap – the smaller the width, the higher is the stability boundary.

Fig. 4
figure 4

Stability diagram for simply supported (a) and cantilevered (b) coaxial shells at different values of the annular gap width k

Full size image

4 Conclusion

In this paper, a mathematical statement of the loss-of-stability problem and a finite element algorithm for its numerical simulation have been proposed to study the dynamic behavior of single elastic and coaxial cylindrical shells of revolution subject to compressible fluid flows having axial and tangential velocity components. Numerical calculations have shown that for both examined configurations the stability boundary, which has been determined by assigning a fixed value to one of the velocities and exhaustive searching for the critical value of the other velocity, depends on the type of the boundary conditions and linear dimensions. A combined action of both velocity components essentially affects the character of the dynamic behavior of elastic bodies. This effect is more pronounced in the case of cantilevered shells. Moreover, the stabilizing action of the axial flow involves two other effects – a jump-wise change in the critical value of one of the velocity components at a minimum value of the other velocity component and non-monotonic dependence of one velocity component on the other. Such a behavior is caused either by different responses of the cantilevered shell to the axial and tangential velocity components acting separately or by the existence of hydrodynamic damping, which plays a decisive role in the dynamic behavior of the system.